题目链接

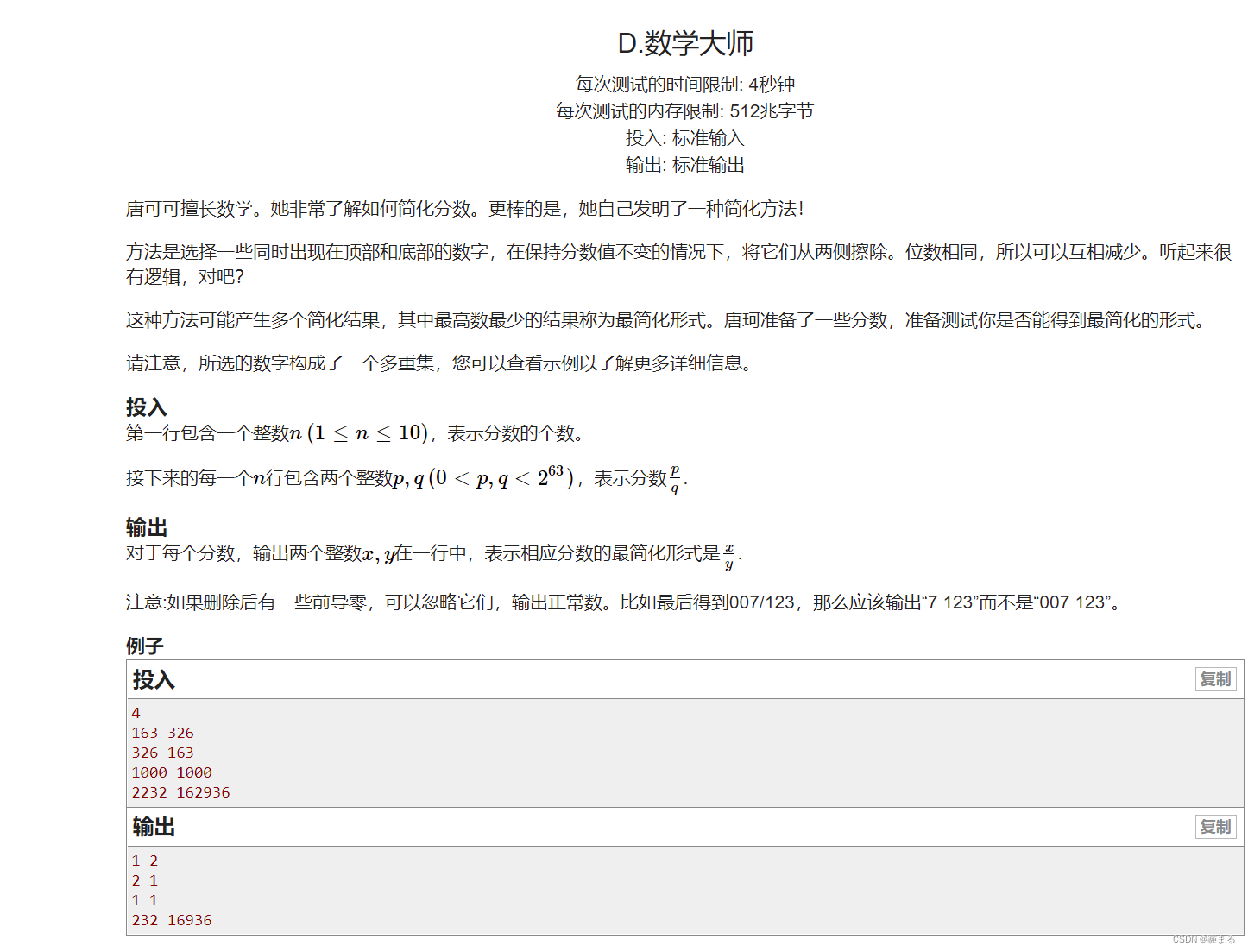
题解

$2^{63}$大概是$10^{19}$那么一共有19位需要讨论, 每一个位数各有保留和删除两种状态, 全部状态就是$2^{18}$种
因为每一位数都有两种状态, 使用二进制数表示每个状态, 正好能全部表示, 在二进制位数下1表示保留, 0表示删除(反过来也一样)
使用二进制暴力搜索每一个符合条件的分子, 先判断删除后是否符合条件, 然后通过
$\frac{暴力求出的分子}{需要求得的分母}=\frac{原分子}{原分母}$得到分母, 这一步需要使用gcd优化$\frac{原分子}{原分母}$为

$$\frac{\frac{原分子}{gcd(原分子,原分母)}}{\frac{原分母}{gcd(原分子,原分母)}}$$
不使用gcd会爆longlong, 当然使用int128的话就不需要这一步了

求出分母后, 与原分母进行对比, 用一个数组存储所有被删除的数字, 与分子中被删除的数字比对, 如果符合条件就更新答案

代码

/*
⣿⣿⣿⣿⣿⣿⡷⣯⢿⣿⣷⣻⢯⣿⡽⣻⢿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣇⠸⣿⣿⣆⠹⣿⣿⢾⣟⣯⣿⣿⣿⣿⣿⣿⣽⣻⣿⣿⣿⣿⣿⣿⣿
⣿⣿⣿⣿⣿⣿⣻⣽⡿⣿⣎⠙⣿⣞⣷⡌⢻⣟⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣷⣿⣿⣿⣿⣿⣿⡄⠹⣿⣿⡆⠻⣿⣟⣯⡿⣽⡿⣿⣿⣿⣿⣽⡷⣯⣿⣿⣿⣿⣿⣿
⣿⣿⣿⣿⣿⣿⣟⣷⣿⣿⣿⡀⠹⣟⣾⣟⣆⠹⣯⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡇⢠⡘⣿⣿⡄⠉⢿⣿⣽⡷⣿⣻⣿⣿⣿⣿⡝⣷⣯⢿⣿⣿⣿⣿
⣿⣿⣿⣿⣿⣿⣯⢿⣾⢿⣿⡄⢄⠘⢿⣞⡿⣧⡈⢷⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡇⢸⣧⠘⣿⣷⠈⣦⠙⢿⣽⣷⣻⣽⣿⣿⣿⣿⣌⢿⣯⢿⣿⣿⣿
⣿⣿⣿⣿⣿⣿⣟⣯⣿⢿⣿⡆⢸⡷⡈⢻⡽⣷⡷⡄⠻⣽⣿⣿⡿⣿⣿⣿⣿⣿⣿⣷⣿⣿⣿⣿⣏⢰⣯⢷⠈⣿⡆⢹⢷⡌⠻⡾⢋⣱⣯⣿⣿⣿⣿⡆⢻⡿⣿⣿⣿
⣿⣿⣿⣿⣿⣿⡎⣿⢾⡿⣿⡆⢸⣽⢻⣄⠹⣷⣟⣿⣄⠹⣟⣿⣿⣟⣿⣿⣿⣿⣿⣿⣽⣿⣿⣿⡇⢸⣯⣟⣧⠘⣷⠈⡯⠛⢀⡐⢾⣟⣷⣻⣿⣿⣿⡿⡌⢿⣻⣿⣿
⣿⣿⣿⣿⣿⣿⣧⢸⡿⣟⣿⡇⢸⣯⣟⣮⢧⡈⢿⣞⡿⣦⠘⠏⣹⣿⣽⢿⣿⣿⣿⣿⣯⣿⣿⣿⡇⢸⣿⣿⣾⡆⠹⢀⣠⣾⣟⣷⡈⢿⣞⣯⢿⣿⣿⣿⢷⠘⣯⣿⣿
⣿⣿⣿⣿⣿⣿⣿⡈⣿⢿⣽⡇⠘⠛⠛⠛⠓⠓⠈⠛⠛⠟⠇⢀⢿⣻⣿⣯⢿⣿⣿⣿⣷⢿⣿⣿⠁⣾⣿⣿⣿⣧⡄⠇⣹⣿⣾⣯⣿⡄⠻⣽⣯⢿⣻⣿⣿⡇⢹⣾⣿
⣿⣿⣿⣿⣿⣿⣿⡇⢹⣿⡽⡇⢸⣿⣿⣿⣿⣿⣞⣆⠰⣶⣶⡄⢀⢻⡿⣯⣿⡽⣿⣿⣿⢯⣟⡿⢀⣿⣿⣿⣿⣿⣧⠐⣸⣿⣿⣷⣿⣿⣆⠹⣯⣿⣻⣿⣿⣿⢀⣿⢿
⣿⣿⣿⣿⣿⣿⣿⣿⠘⣯⡿⡇⢸⣿⣿⣿⣿⣿⣿⣿⣧⡈⢿⣳⠘⡄⠻⣿⢾⣽⣟⡿⣿⢯⣿⡇⢸⣿⣿⣿⣿⣿⣿⡀⢾⣿⣿⣿⣿⣿⣿⣆⠹⣾⣷⣻⣿⡿⡇⢸⣿
⣿⣿⣿⣿⣿⣿⣿⣿⡇⢹⣿⠇⢸⣿⣿⣿⣿⣿⣿⣿⣿⣷⣄⠻⡇⢹⣆⠹⣟⣾⣽⣻⣟⣿⣽⠁⣾⣿⣿⣿⣿⣿⣿⣇⣿⣿⠿⠛⠛⠉⠙⠋⢀⠁⢘⣯⣿⣿⣧⠘⣿
⣿⣿⣿⣿⣿⣿⣿⣿⣿⡈⣿⡃⢼⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣦⡙⠌⣿⣆⠘⣿⣞⡿⣞⡿⡞⢠⣿⣿⣿⣿⣿⡿⠛⠉⠁⢀⣀⣠⣤⣤⣶⣶⣶⡆⢻⣽⣞⡿⣷⠈⣿
⣿⣿⣿⣿⣿⣿⣿⣿⡿⠃⠘⠁⠉⠉⠉⠉⠉⠉⠉⠉⠉⠙⠛⠛⢿⣄⢻⣿⣧⠘⢯⣟⡿⣽⠁⣾⣿⣿⣿⣿⣿⡃⢀⢀⠘⠛⠿⢿⣻⣟⣯⣽⣻⣵⡀⢿⣯⣟⣿⢀⣿
⣿⣿⣿⣟⣿⣿⣿⣿⣶⣶⡆⢀⣿⣾⣿⣾⣷⣿⣶⠿⠚⠉⢀⢀⣤⣿⣷⣿⣿⣷⡈⢿⣻⢃⣼⣿⣿⣿⣿⣻⣿⣿⣿⡶⣦⣤⣄⣀⡀⠉⠛⠛⠷⣯⣳⠈⣾⡽⣾⢀⣿
⣿⢿⣿⣿⣻⣿⣿⣿⣿⣿⡿⠐⣿⣿⣿⣿⠿⠋⠁⢀⢀⣤⣾⣿⣿⣿⣿⣿⣿⣿⣿⣌⣥⣾⡿⣿⣿⣷⣿⣿⢿⣷⣿⣿⣟⣾⣽⣳⢯⣟⣶⣦⣤⡾⣟⣦⠘⣿⢾⡁⢺
⣿⣻⣿⣿⡷⣿⣿⣿⣿⣿⡗⣦⠸⡿⠋⠁⢀⢀⣠⣴⢿⣿⣽⣻⢽⣾⣟⣷⣿⣟⣿⣿⣿⣳⠿⣵⣧⣼⣿⣿⣿⣿⣿⣾⣿⣿⣿⣿⣿⣽⣳⣯⣿⣿⣿⣽⢀⢷⣻⠄⠘
⣿⢷⣻⣿⣿⣷⣻⣿⣿⣿⡷⠛⣁⢀⣀⣤⣶⣿⣛⡿⣿⣮⣽⡻⣿⣮⣽⣻⢯⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣯⢀⢸⣿⢀⡆
⠸⣟⣯⣿⣿⣷⢿⣽⣿⣿⣷⣿⣷⣆⠹⣿⣶⣯⠿⣿⣶⣟⣻⢿⣷⣽⣻⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⢀⣯⣟⢀⡇
⣇⠹⣟⣾⣻⣿⣿⢾⡽⣿⣿⣿⣿⣿⣆⢹⣶⣿⣻⣷⣯⣟⣿⣿⣽⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡿⢀⡿⡇⢸⡇
⣿⣆⠹⣷⡻⣽⣿⣯⢿⣽⣻⣿⣿⣿⣿⣆⢻⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⠛⢻⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⠇⢸⣿⠇⣼⡇
⡙⠾⣆⠹⣿⣦⠛⣿⢯⣷⢿⡽⣿⣿⣿⣿⣆⠻⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⠃⠎⢸⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⠏⢀⣿⣾⣣⡿⡇
⣿⣷⡌⢦⠙⣿⣿⣌⠻⣽⢯⣿⣽⣻⣿⣿⣿⣧⠩⢻⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡏⢰⢣⠘⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡿⠃⢀⢀⢿⣞⣷⢿⡇
⣿⣽⣆⠹⣧⠘⣿⣿⡷⣌⠙⢷⣯⡷⣟⣿⣿⣿⣷⡀⡹⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣷⣈⠃⣸⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⠟⢀⣴⡧⢀⠸⣿⡽⣿⢀
⢻⣽⣿⡄⢻⣷⡈⢿⣿⣿⢧⢀⠙⢿⣻⡾⣽⣻⣿⣿⣄⠌⢿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⠛⢁⣰⣾⣟⡿⢀⡄⢿⣟⣿⢀
⡄⢿⣿⣷⢀⠹⣟⣆⠻⣿⣿⣆⢀⣀⠉⠻⣿⡽⣯⣿⣿⣷⣈⢻⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡿⠋⢀⣠⠘⣯⣷⣿⡟⢀⢆⠸⣿⡟⢸
⣷⡈⢿⣿⣇⢱⡘⢿⣷⣬⣙⠿⣧⠘⣆⢀⠈⠻⣷⣟⣾⢿⣿⣆⠹⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡿⠋⣠⡞⢡⣿⢀⣿⣿⣿⠇⡄⢸⡄⢻⡇⣼
⣿⣷⡈⢿⣿⡆⢣⡀⠙⢾⣟⣿⣿⣷⡈⠂⠘⣦⡈⠿⣯⣿⢾⣿⣆⠙⠻⠿⠿⠿⠿⡿⣿⣿⣿⣿⣿⣿⣿⣿⣿⠿⠛⢋⣠⣾⡟⢠⣿⣿⢀⣿⣿⡟⢠⣿⢈⣧⠘⢠⣿
⣿⣿⣿⣄⠻⣿⡄⢳⡄⢆⡙⠾⣽⣿⣿⣆⡀⢹⡷⣄⠙⢿⣿⡾⣿⣆⢀⡀⢀⢀⢀⢀⢀⢀⢀⢀⢀⢀⢀⢀⣀⣠⣴⡿⣯⠏⣠⣿⣿⡏⢸⣿⡿⢁⣿⣿⢀⣿⠆⢸⣿
⣿⣿⣿⣿⣦⡙⣿⣆⢻⡌⢿⣶⢤⣉⣙⣿⣷⡀⠙⠽⠷⠄⠹⣿⣟⣿⣆⢙⣋⣤⣤⣤⣄⣀⢀⢀⢀⢀⣾⣿⣟⡷⣯⡿⢃⣼⣿⣿⣿⠇⣼⡟⣡⣿⣿⣿⢀⡿⢠⠈⣿
⣿⣿⣿⣿⣿⣷⣮⣿⣿⣿⡌⠁⢤⣤⣤⣤⣬⣭⣴⣶⣶⣶⣆⠈⢻⣿⣿⣆⢻⣿⣿⣿⣿⣿⣿⣷⣶⣤⣌⣉⡘⠛⠻⠶⣿⣿⣿⣿⡟⣰⣫⣴⣿⣿⣿⣿⠄⣷⣿⣿⣿
*/
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <queue>
#include <cmath>
#include <cstring>
#include <string>
#include <stack>
#include <deque>
#include <map>
#include <set>
#include <bitset>
#include <unordered_map>
#include <unordered_set>
using namespace std;
#define ll long long
#define endl "\n"
#define S second
#define F first
#define ln cout<<endl;
#define rep(i, a, b) for (ll i = (a); i <= (b); i++)
#define repr(i, a, b) for (ll i = (a); i < (b); i++)
#define rrep(i, a, b) for (ll i = (b); i >= (a); i--)
#define rrepr(i, a, b) for (ll i = (b); i > (a); i--)
#define mem(a) memset((a),0,sizeof (a));
#define yes cout<<"YES"<<endl;
#define no cout<<"NO"<<endl;
#define debug cout<<"here!"<<endl;

ll cnt,n,m,t,ans,ant;
const int N=2e5+10;
const int INF=0x3f3f3f3f;
const ll llINF=0x3f3f3f3f3f3f3f3f;
ll arr[N];
ll tmp[10],vis[10];
string str;
string a,b;
ll a1,b1,asize,bsize;

inline ll read()
{
    char c = getchar();int x = 0,s = 1;
    while(c < '0' || c > '9') {if(c == '-') s = -1;c = getchar();}//是符号
    while(c >= '0' && c <= '9') {x = x*10 + c -'0';c = getchar();}//是数字
    return x*s;
}

ll check(ll x)
{
    rrep(i,0,bsize-1)//倒序是因为从个位数开始检查
    {
        if(b[i]-'0'==x%10) x/=10;
        else tmp[b[i]-'0']++;
    }
    if(x) return 0;
    rep(i,0,9) 
        if(vis[i]!=tmp[i]) return 0;
    return 1;
}

ll atoi(string p)//atoi的类型是int 重写atoi函数
{
    ll sum=0;
    rep(i,0,p.size()-1)
    {
        sum*=10ll;
        sum+=p[i]-'0';
    }
    return sum;
}

void solve()
{
    cin>>a>>b;
    a1=atoi(a);
    b1=atoi(b);

    asize=a.size();
    bsize=b.size();

    ll ans1,ans2;//存答案
    ans1=a1;
    ans2=b1;

    ll x,y;
    x=a1/__gcd(a1,b1);
    y=b1/__gcd(a1,b1);//防止爆ll

    rep(i,0,1<<asize)
    {
        fill(tmp,tmp+10,0);
        fill(vis,vis+10,0);//初始化
        ll q,p;
        q=p=0;

        repr(j,0,asize)//二进制位表示每位数删和不删 1表示保留 0表示删去
        {
            if((i>>j)&1) q=q*10ll+a[j]-'0';//保留
            else vis[a[j]-'0']++;//删除
        }
        if(q==0||q*y%x) continue;//y是分母, 保留下来的数(分子)*分母%分子==0说明条件成立
        p=q*y/x;//通过分子求分母 $$ q/p=x/y $$
        if(check(p))
        {
            ans1=min(ans1,q);
            ans2=min(ans2,p);
        }
    }
    cout<<ans1<<' '<<ans2<<endl;


    return;
}

int main()
{
    ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
    //所有输入用cin
    //所有输出用cout
	
    cin>>t;
    while(t--)
        solve();
    return 0;
}