作者:小树苗渴望变成参天大树
作者宣言:认真写好每一篇博客
作者gitee:gitee
如 果 你 喜 欢 作 者 的 文 章 ,就 给 作 者 点 点 关 注 吧!
文章目录
- 前言
- 一、递归版本
- 二、非递归版本
- 三、总结
前言
今天我们再来将一个排序,这个排序,特别不好理解,尤其是非递归,递归版本还可以,它就是归并排序,我们知道两个有序的数组,通过第三个数组就会整体变成有序,数组中只有一个元素的时候南无这就是一个有序数组,我们利用这个思想就来进行归并,接下来就来听我讲解归并排序吧
一、递归版本
思想的铺垫:
我们先来看看两个有序的数组怎么通过第三个数组来变成·整体有序的吧
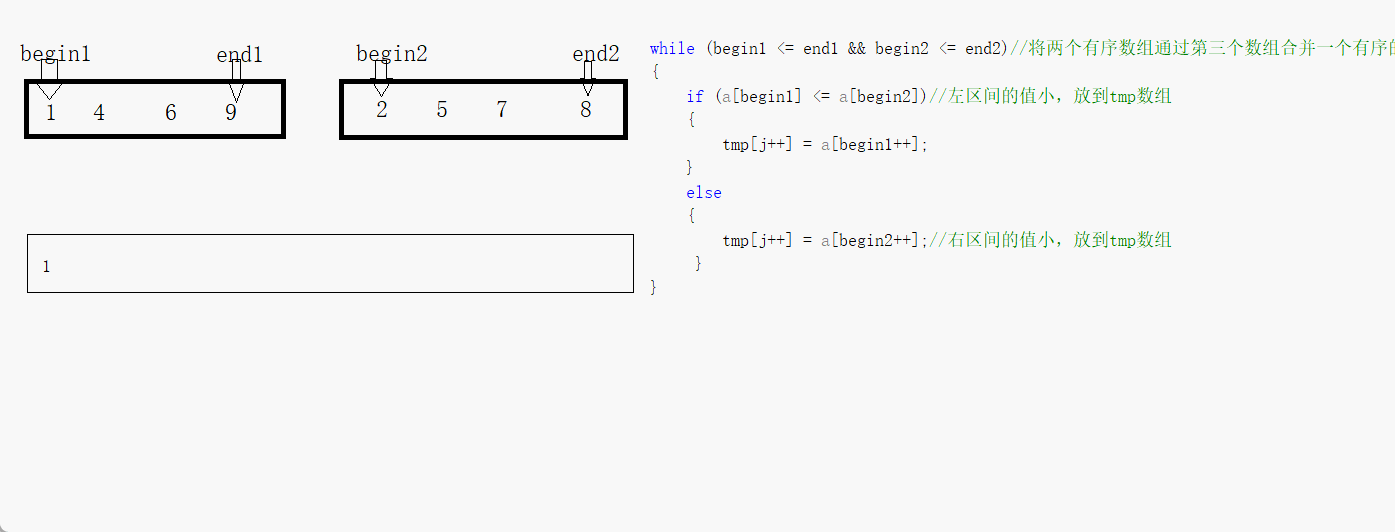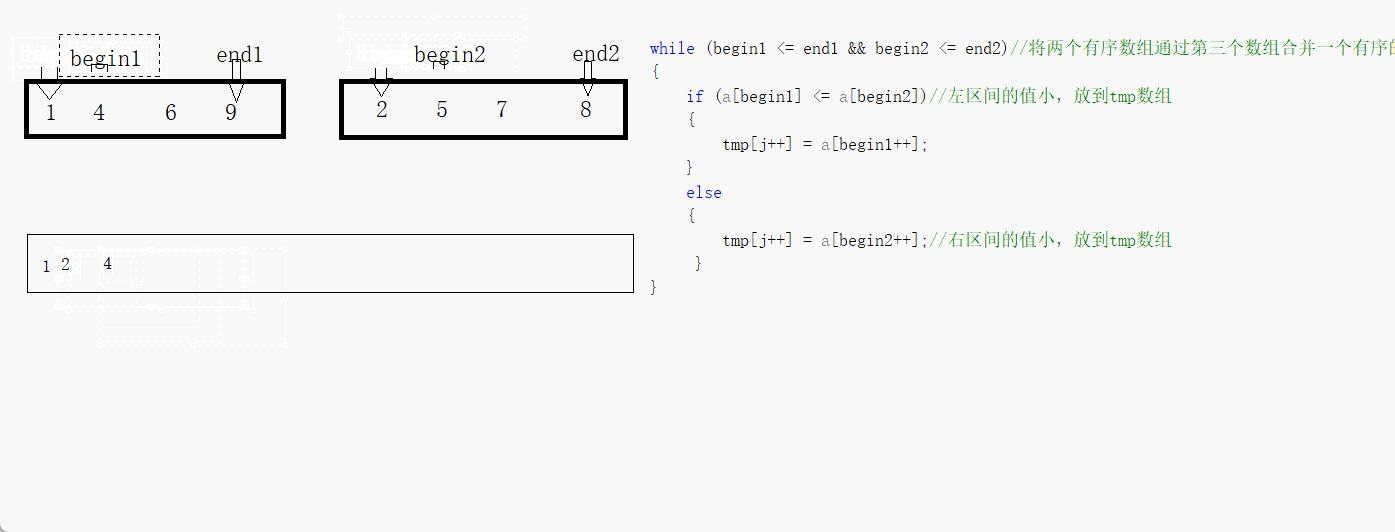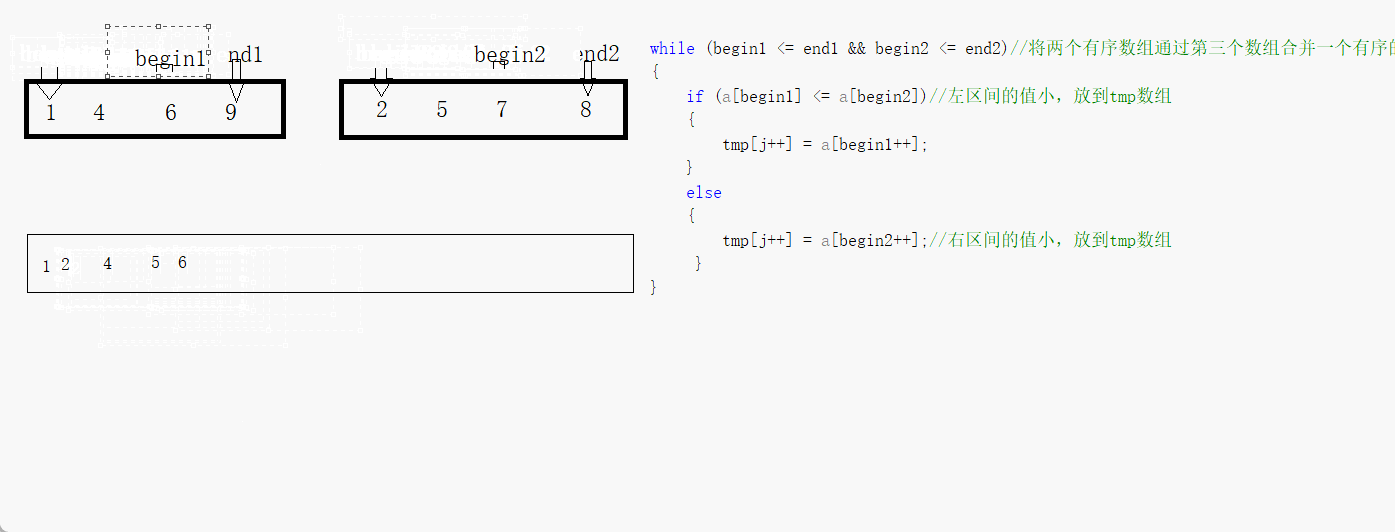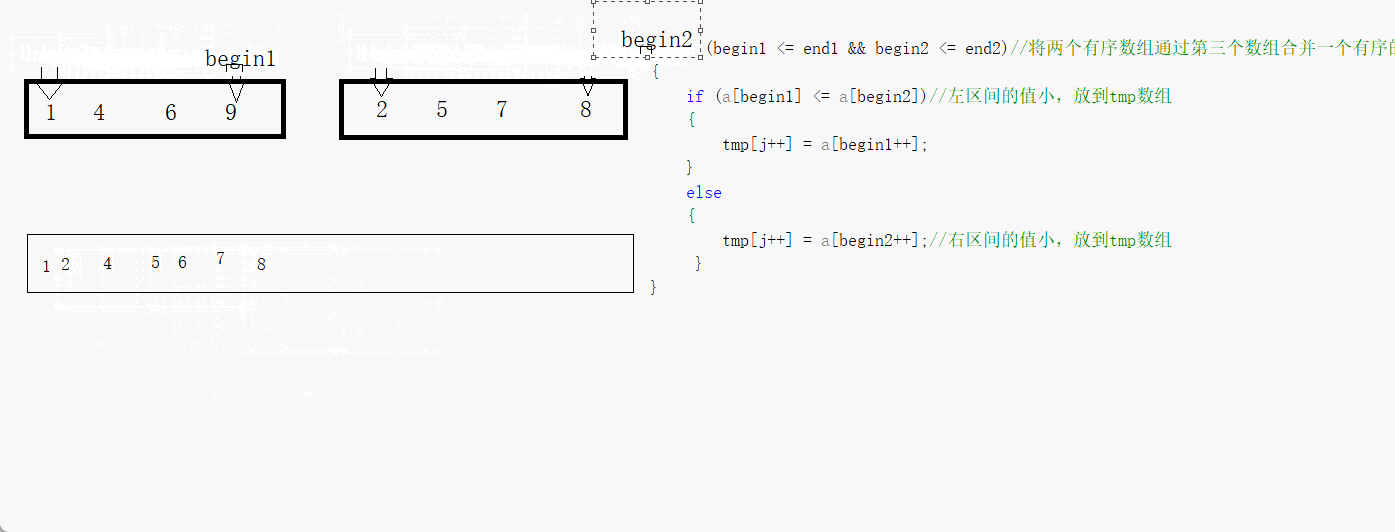
我们看到只要一个结束整体就结束,那个没有结束的再通过循环来赋值到第三个数组
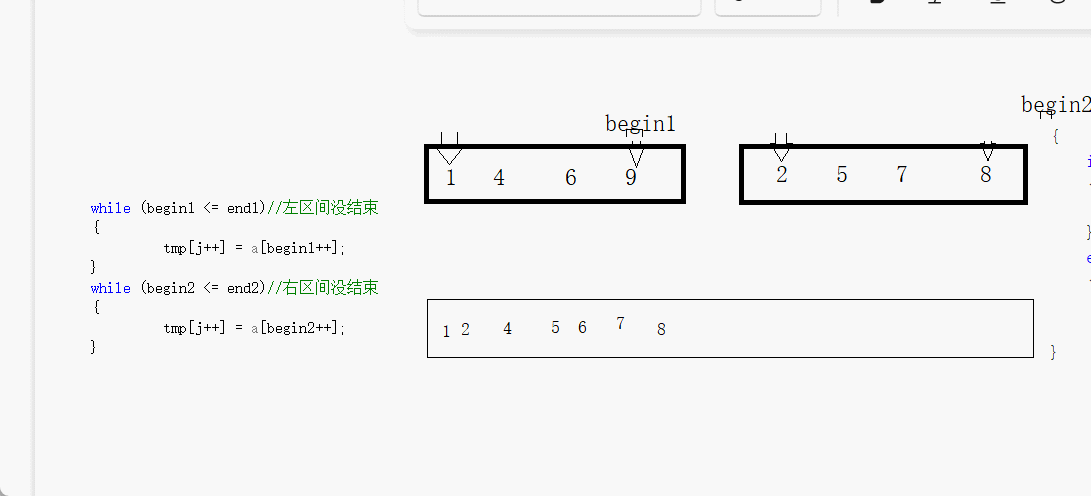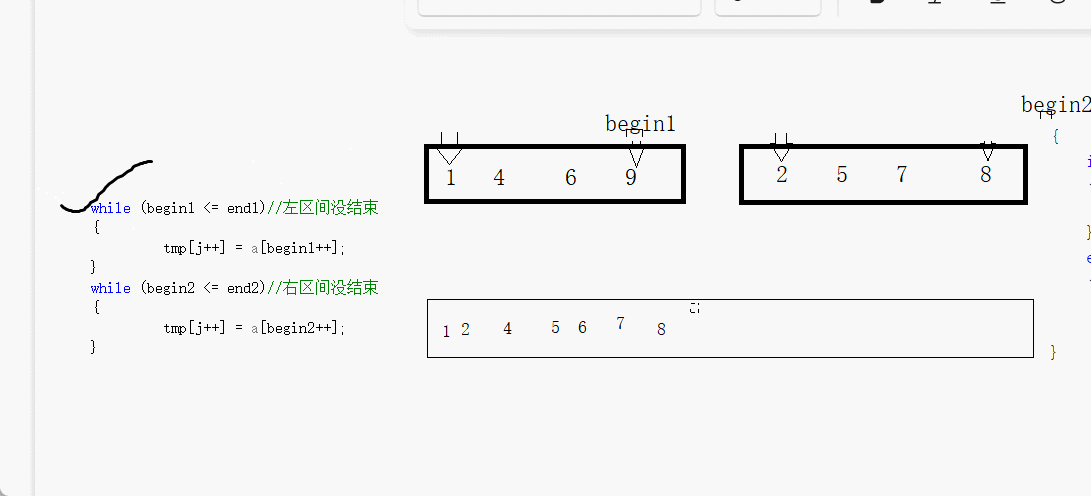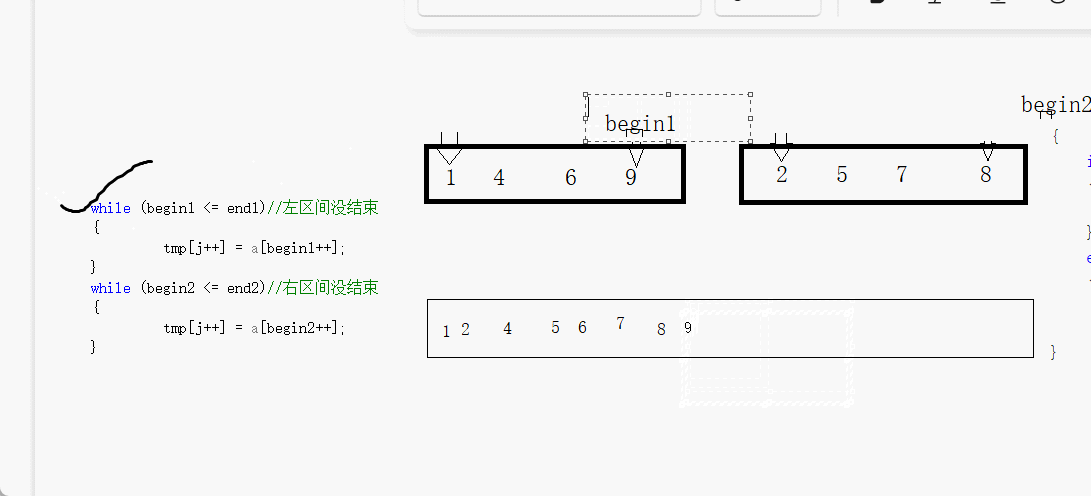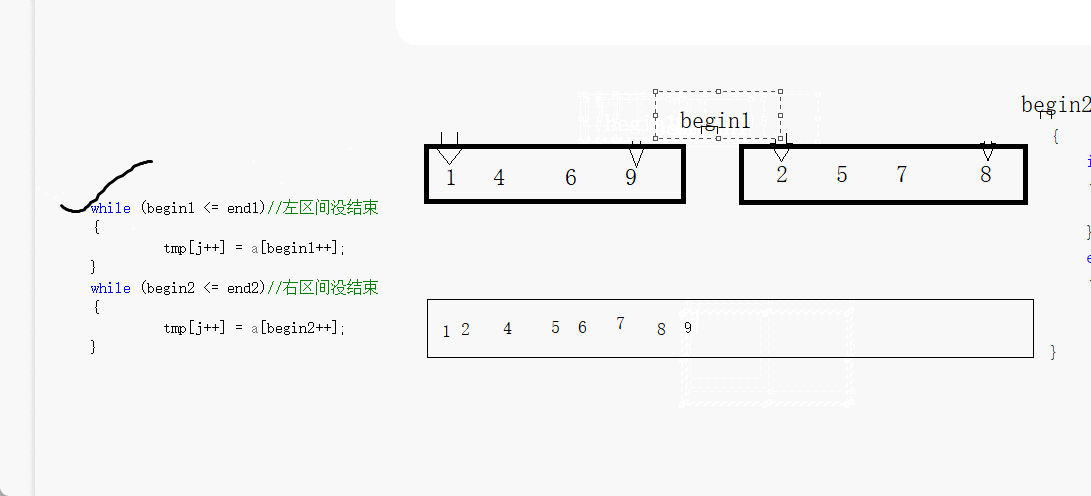
我们一会就通过第三个数组就两个有序数组归并成整体有序的数组
归并排序的思想:
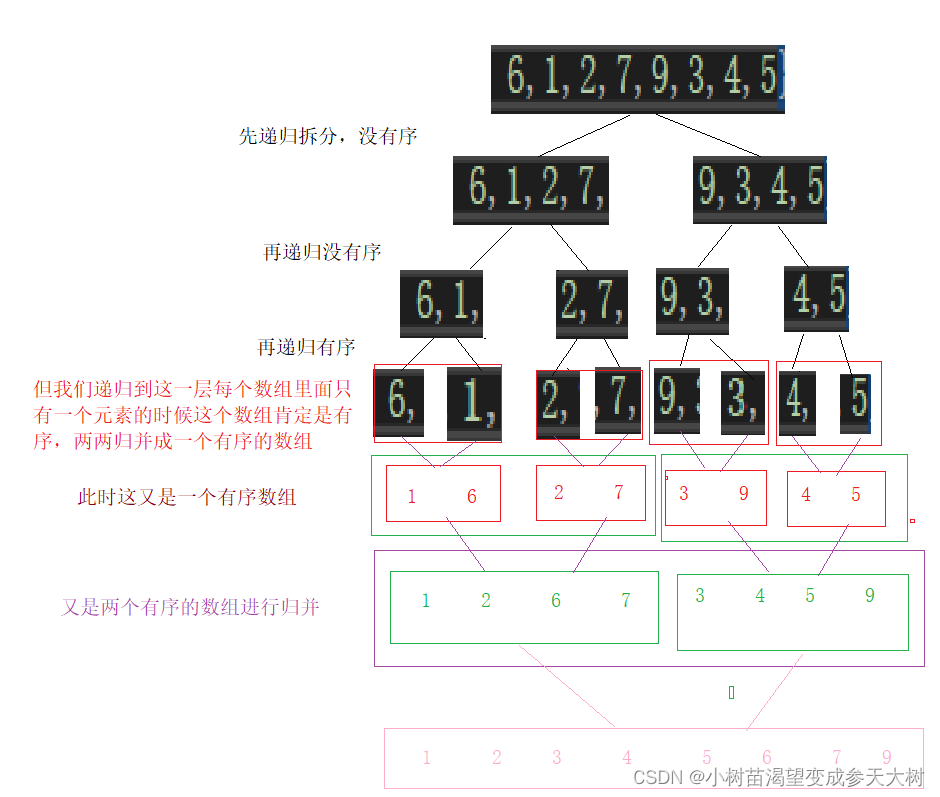
因为再递归的过程我们不知道这两个数组是否,只能保证递归到只有一个元素的时候是有序的,就不用递归,就就是递归结束的条件,并且不知道中途是否有序,我们只能把两个区间都递归到最后一层,先将左边有序,再将右边有序,最后再将根有序
但我们是在一个数组里面,怎么变成两个数组呢??不可能开辟两个数组把分开的,我们采取区间划分的方法即可,这样就是两个数组,我们通过第三个数组来变成有序,最后还是需要拷贝回原数组
那现在有一个问题,我们每次归并都要开辟数组进行排序吗??那样太麻烦了,我们通过定义一个子函数,进行归并,外面的函数开辟一次就够了,通过下表来控制,排序和拷贝回去应该什么那个位置的数据
我们来看函数整体:
void _MergeSort(int* a, int left, int right, int* tmp)
{
if (left >= right)//结束条件
return;
int mid = (left + right) / 2;//划分区间,为两个数组
_MergeSort(a, left, mid, tmp);
_MergeSort(a, mid+1, right, tmp);//类似为二叉树的后序遍历,因为要先递归到两个数组只有一个元素的时候,因为数组只有一个元素的时候肯定是有序的
int begin1 = left; int end1 = mid;//左区间左右下标
int begin2 = mid + 1; int end2 = right;//右区间左右下标
int index = left;
while (begin1 <= end1 && begin2 <= end2)//将两个有序数组通过第三个数组合并一个有序的
{
if (a[begin1] <= a[begin2])//左区间的值小,放到tmp数组
{
tmp[index++] = a[begin1++];
}
else
{
tmp[index++] = a[begin2++];//右区间的值小,放到tmp数组
}
}
while (begin1 <= end1)//左区间没结束
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2)//右区间没结束
{
tmp[index++] = a[begin2++];
}
for (int i = 0; i <index; i++)//拷贝回原数组
{
a[i] = tmp[i];
}
}
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);//开辟一个和原数组一样的空间
if(tmp == NULL)
{
perror("malloc fail");
}
_MergeSort(a,0,n-1,tmp);
free(tmp);
}
我们仔细看看子函数里面的内容,有没有特别像二叉树里面的后序遍历,可能之前不懂,但是你看过代码之后肯定就会理解了,有的小伙伴当心,tmp拷贝回去不会有下标冲突的问题吗??这个完全不用担心,因为·我们再递归·的时候都把下标严格区分开,不会有第一个数组和第二个数组有交叉的下标,也不会有下标没有递归进去
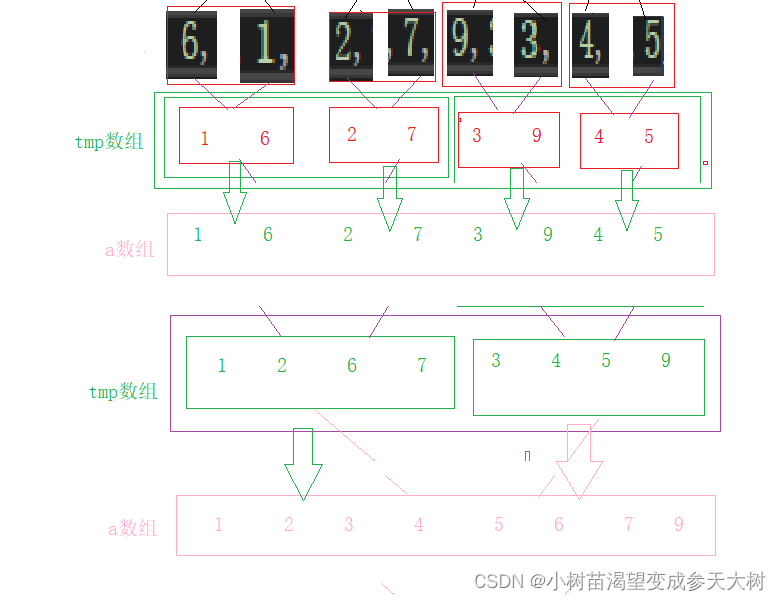
希望大家可以好好理解,因为接下来将的非递归才是最难理解的
二、非递归版本
我们再递归的基础上,来想想,我们是通过直接递归到左右区间只有一个元素的时候,那我们不用递归,直接通过原数组来把区间先画分成只有一个元素不久好了,然后再划分成两个,四个,我们来看看图解:
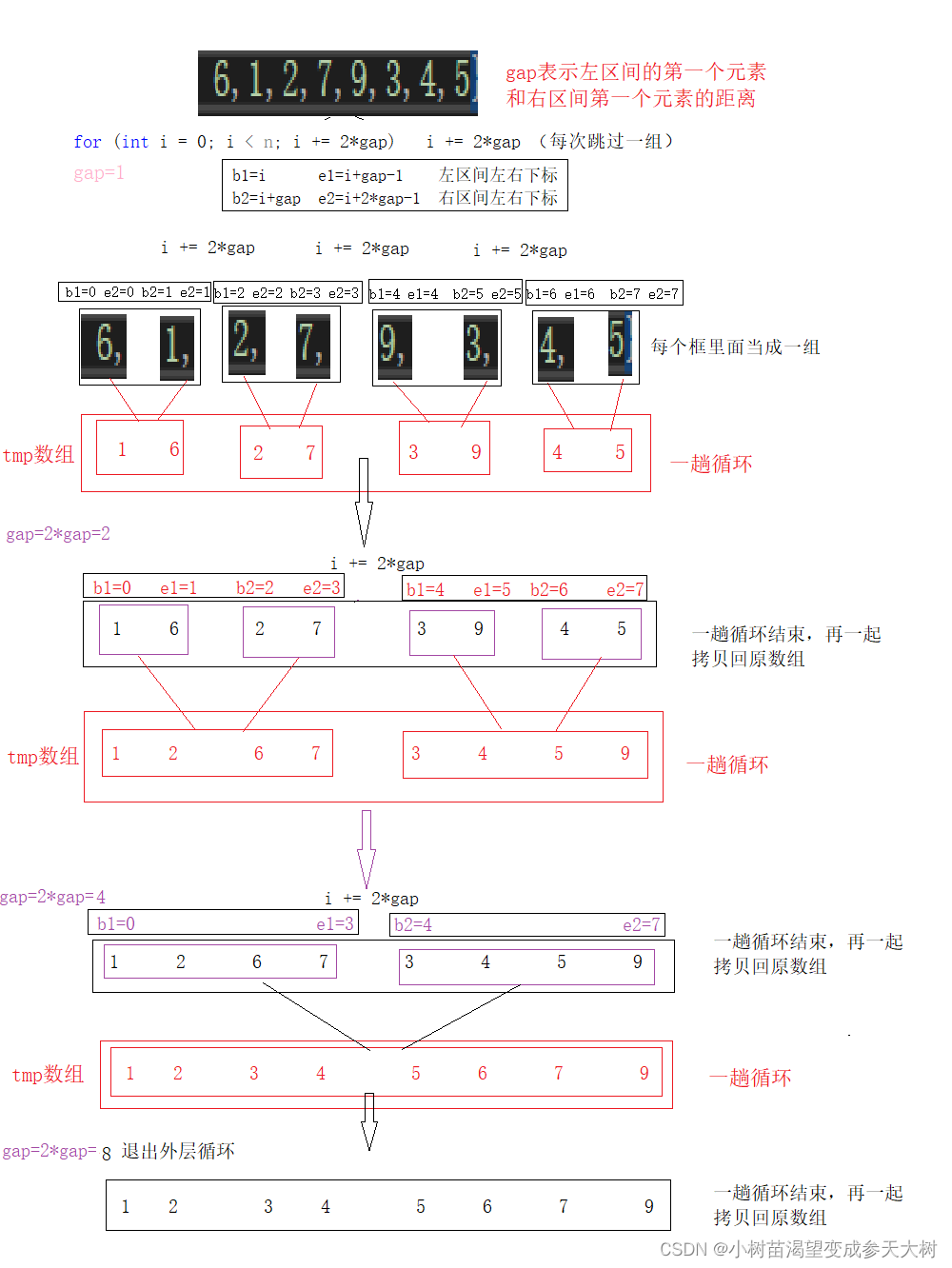
我们根据这个图来些一下一趟的排序代码:
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
}
int gap = 1; int j = 0;
for (int i = 0; i < n; i += 2*gap)
{
//下标是靠自己找关系找出来的
int begin1 = i; int end1 = i + gap-1;
int begin2 = i + gap; int end2 = i +2*gap -1;
while (begin1 <= end1 && begin2 <= end2)//将两个有序数组通过第三个数组合并一个有序的
{
if (a[begin1] <= a[begin2])//左区间的值小,放到tmp数组
{
tmp[j++] = a[begin1++];
}
else
{
tmp[j++] = a[begin2++];//右区间的值小,放到tmp数组
}
}
while (begin1 <= end1)//左区间没结束
{
tmp[j++] = a[begin1++];
}
while (begin2 <= end2)//右区间没结束
{
tmp[j++] = a[begin2++];
}
}
for (int i = 0; i < n; i++)//拷贝回原数组
{
a[i] = tmp[i];
}
free(tmp);
我们来看一趟的运行结果
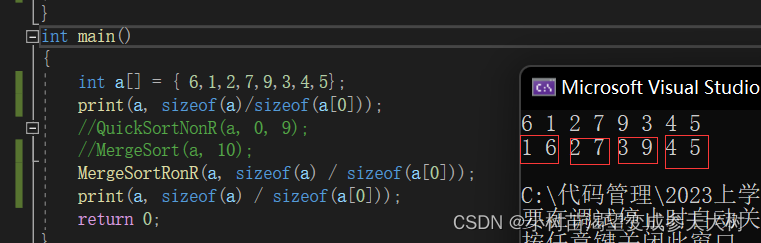
我们还要更新gap的值,所以我们外卖呢再套一个循环让gap走起来,来看一下完整代码:
void MergeSortRonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
}
int gap = 1;
while (gap < n)
{
int j = 0;
for (int i = 0; i < n; i += 2 * gap)
{
int begin1 = i; int end1 = i + gap - 1;
int begin2 = i + gap; int end2 = i + 2 * gap - 1;
while (begin1 <= end1 && begin2 <= end2)//将两个有序数组通过第三个数组合并一个有序的
{
if (a[begin1] <= a[begin2])//左区间的值小,放到tmp数组
{
tmp[j++] = a[begin1++];
}
else
{
tmp[j++] = a[begin2++];//右区间的值小,放到tmp数组
}
}
while (begin1 <= end1)//左区间没结束
{
tmp[j++] = a[begin1++];
}
while (begin2 <= end2)//右区间没结束
{
tmp[j++] = a[begin2++];
}
}
for (int i = 0; i < n; i++)//拷贝回原数组
{
a[i] = tmp[i];
}
gap *= 2;//迭代
}
free(tmp);
}
注意: 相信大家看到这里就觉得结束了吗??非递归也不过如此嘛,真的是这样吗??我们再来测试一组数据:
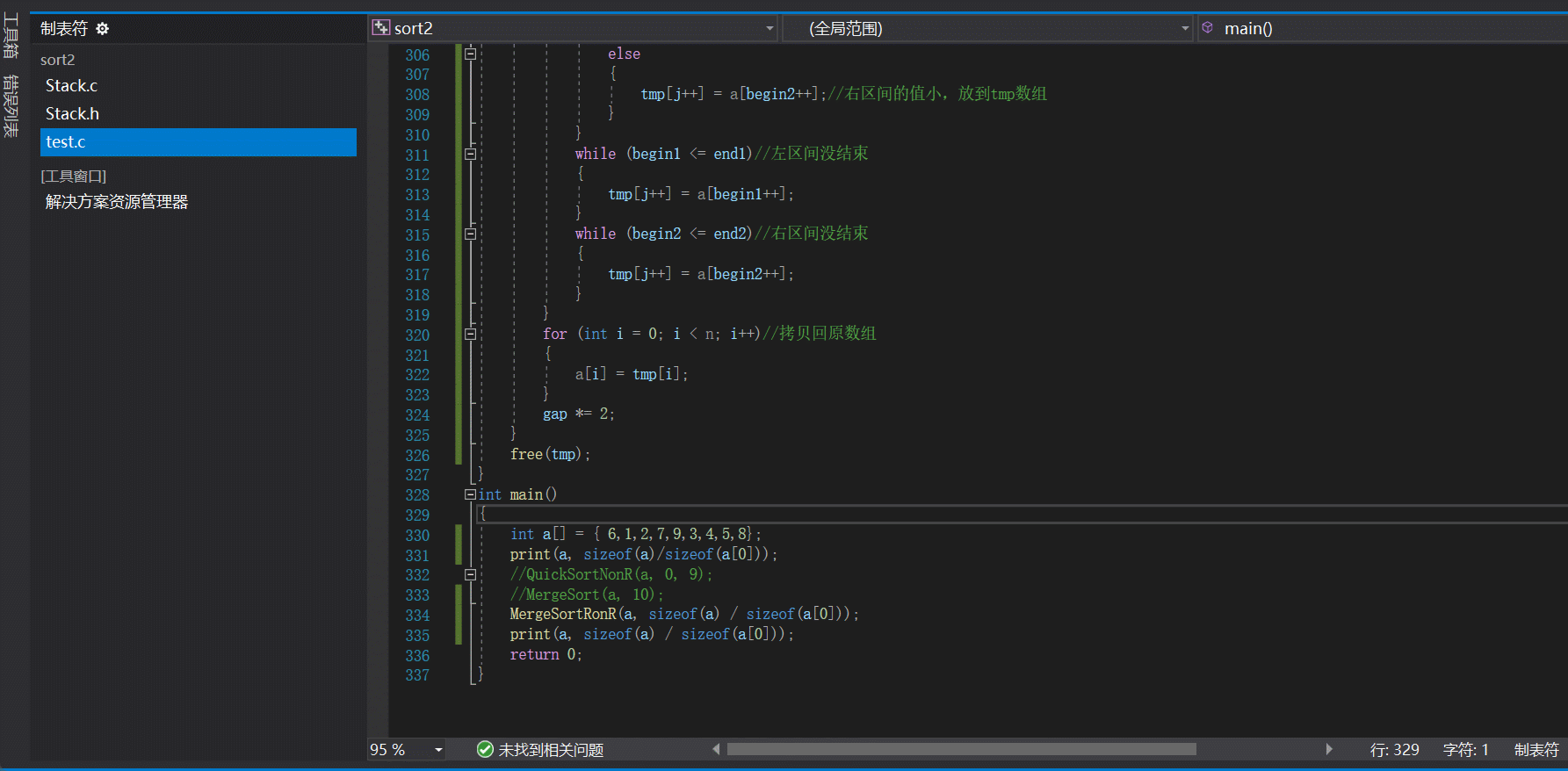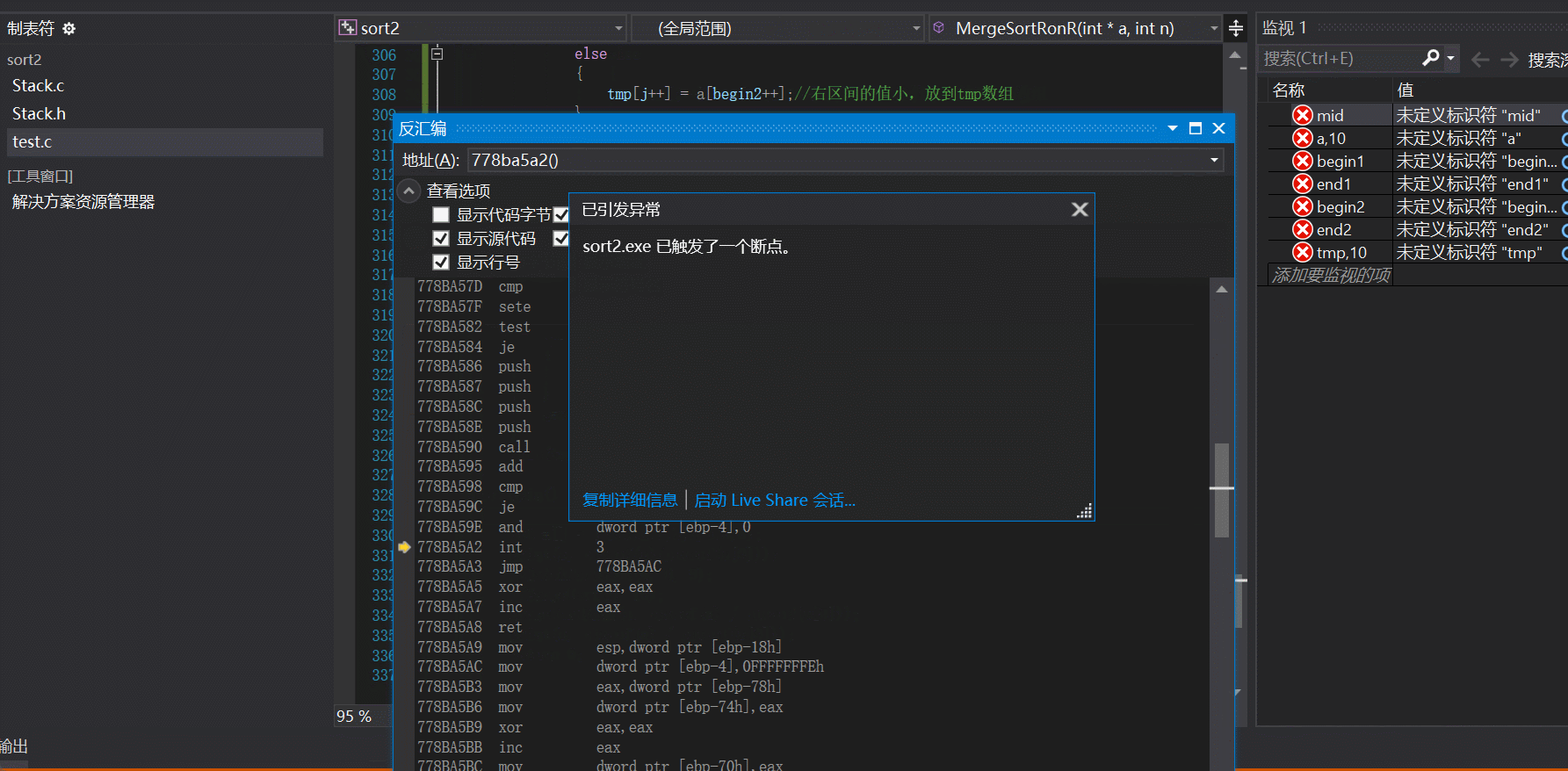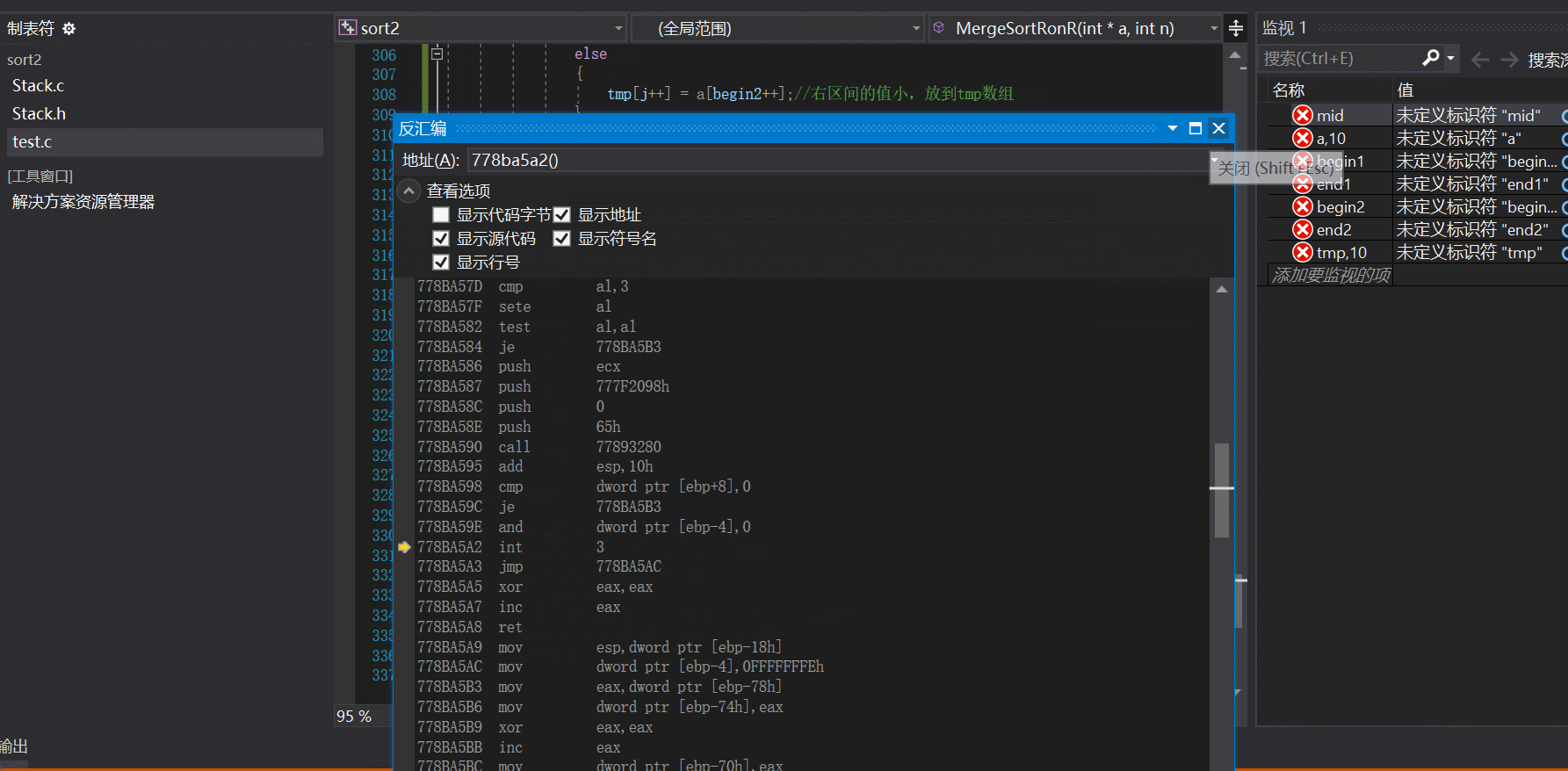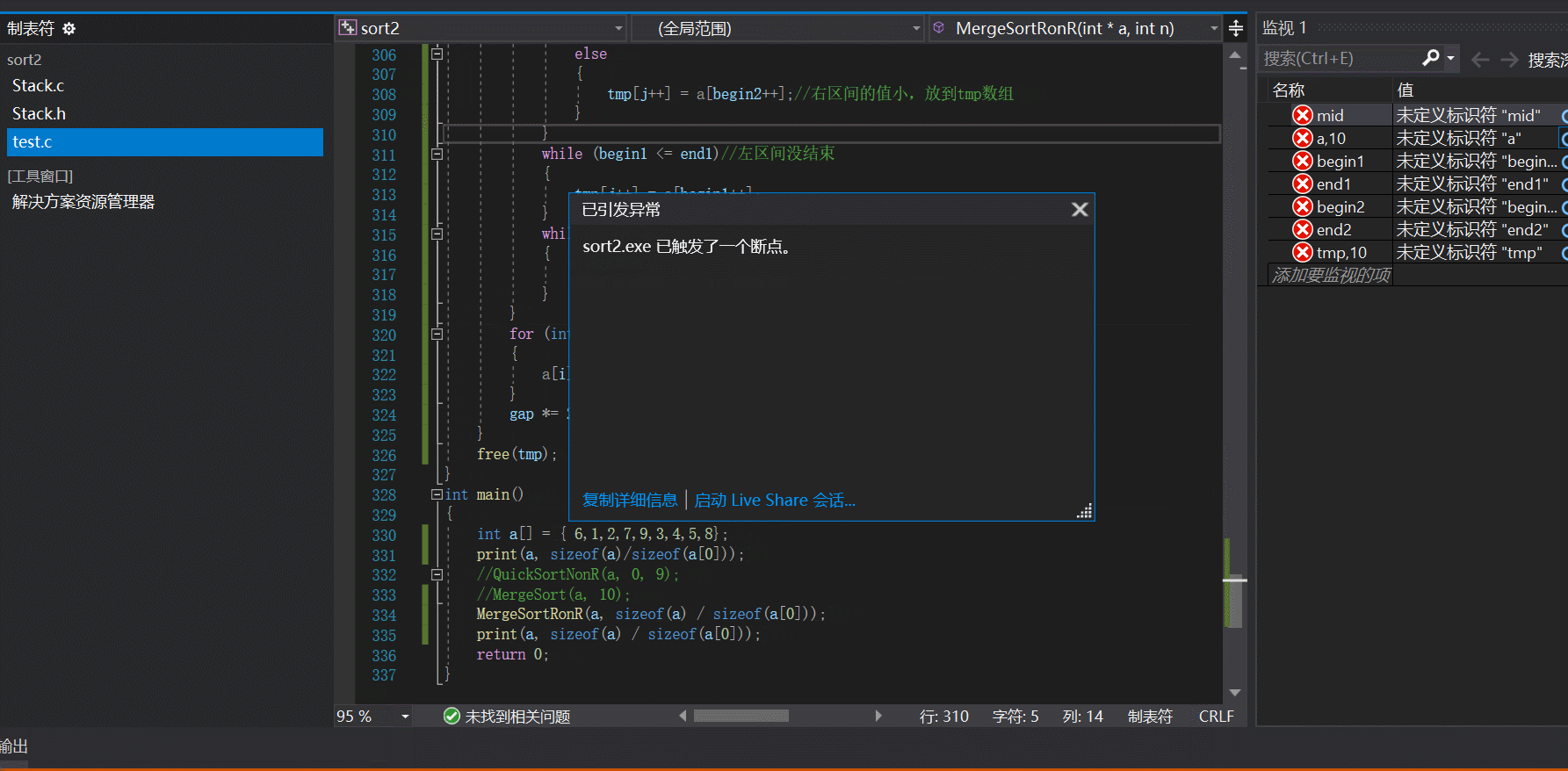
我们发现出现断点错误,一般这种都是说明数组可能越界了,既然这样我们把每一组的下边打印出来看看


我们看到有的数据越界了,那这样我们就找到了问题所在,因为我们是最后整体把数据拷贝回去,所以我们比较把越界的下标修正,导到tmp数组里面,再一起导回原数组,如果归并一次就拷回去就不用担心这个问题,直接返回就好了我们来分析一下越界情况,来看图解:

我们再来看看修正后的前后对比:

最终非递归代码:
void MergeSortRonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
}
int gap = 1;
while (gap < n)
{
int j = 0;
for (int i = 0; i < n; i += 2*gap)
{
int begin1 = i; int end1 = i + gap-1;
int begin2 = i + gap; int end2 = i +2*gap -1;
if (end1 >= n)//进行修正
{
end1 = n - 1;
begin2 = n-1;
end2 = n - 2;
}
else if (begin2 >= n)
{
begin2 = n-1;
end2 = n - 2;
}
else if(end2>=n)
{
end2 = n - 1;
}
while (begin1 <= end1 && begin2 <= end2)//将两个有序数组通过第三个数组合并一个有序的
{
if (a[begin1] <= a[begin2])//左区间的值小,放到tmp数组
{
tmp[j++] = a[begin1++];
}
else
{
tmp[j++] = a[begin2++];//右区间的值小,放到tmp数组
}
}
while (begin1 <= end1)//左区间没结束
{
tmp[j++] = a[begin1++];
}
while (begin2 <= end2)//右区间没结束
{
tmp[j++] = a[begin2++];
}
}
for (int i = 0; i < n; i++)//拷贝回原数组
{
a[i] = tmp[i];
}
gap *= 2;
}
free(tmp);
}
简化的非递归版本:
刚才那种思想是,一趟归并之后,我们一起拷贝回原数组,我们也可以一边归并一边拷贝,把拷贝放到循环里面,那就要改一下拷贝的下标为[0,end2],我们来看代码:
void MergeSortRonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
}
int gap = 1;
while (gap < n)
{
int j = 0;
for (int i = 0; i < n; i += 2 * gap)
{
int begin1 = i; int end1 = i + gap - 1;
int begin2 = i + gap; int end2 = i + 2 * gap - 1;
if (end1 >= n || begin2 >= n)//不需要拷贝
{
break;
}
if (end2 >= n)
{
end2 = n - 1;
}
while (begin1 <= end1 && begin2 <= end2)//将两个有序数组通过第三个数组合并一个有序的
{
if (a[begin1] <= a[begin2])//左区间的值小,放到tmp数组
{
tmp[j++] = a[begin1++];
}
else
{
tmp[j++] = a[begin2++];//右区间的值小,放到tmp数组
}
}
while (begin1 <= end1)//左区间没结束
{
tmp[j++] = a[begin1++];
}
while (begin2 <= end2)//右区间没结束
{
tmp[j++] = a[begin2++];
}
for (int j =0 ; j <=end2; j++)//拷贝回原数组
{
a[j] = tmp[j];
}
}
gap *= 2;
}
free(tmp);
}
相信大家看到这里对归并排序应该了解了,尤其是非递归版本,我们一定要画图,不然下标的控制很容易出错,希望大家可以下来自己去画画图
三、总结
今天关于归并排序的知识点我应该讲清楚了,再这里主流的一些排序我也几乎讲完了,接下来我还会将一个排序,也有实际应用,计数排序,是通过不比较数来进行排序的,方法也非常巧妙,欢迎大家来支持我,如果对于我这篇博客有什么不正确的或者建议都可以再评论区指正出来哦,今天的知识就先分享到这里了,我们下篇再见




![[Linux] 基础IO](https://img-blog.csdnimg.cn/352b158f207c45168261a87475d54310.png)