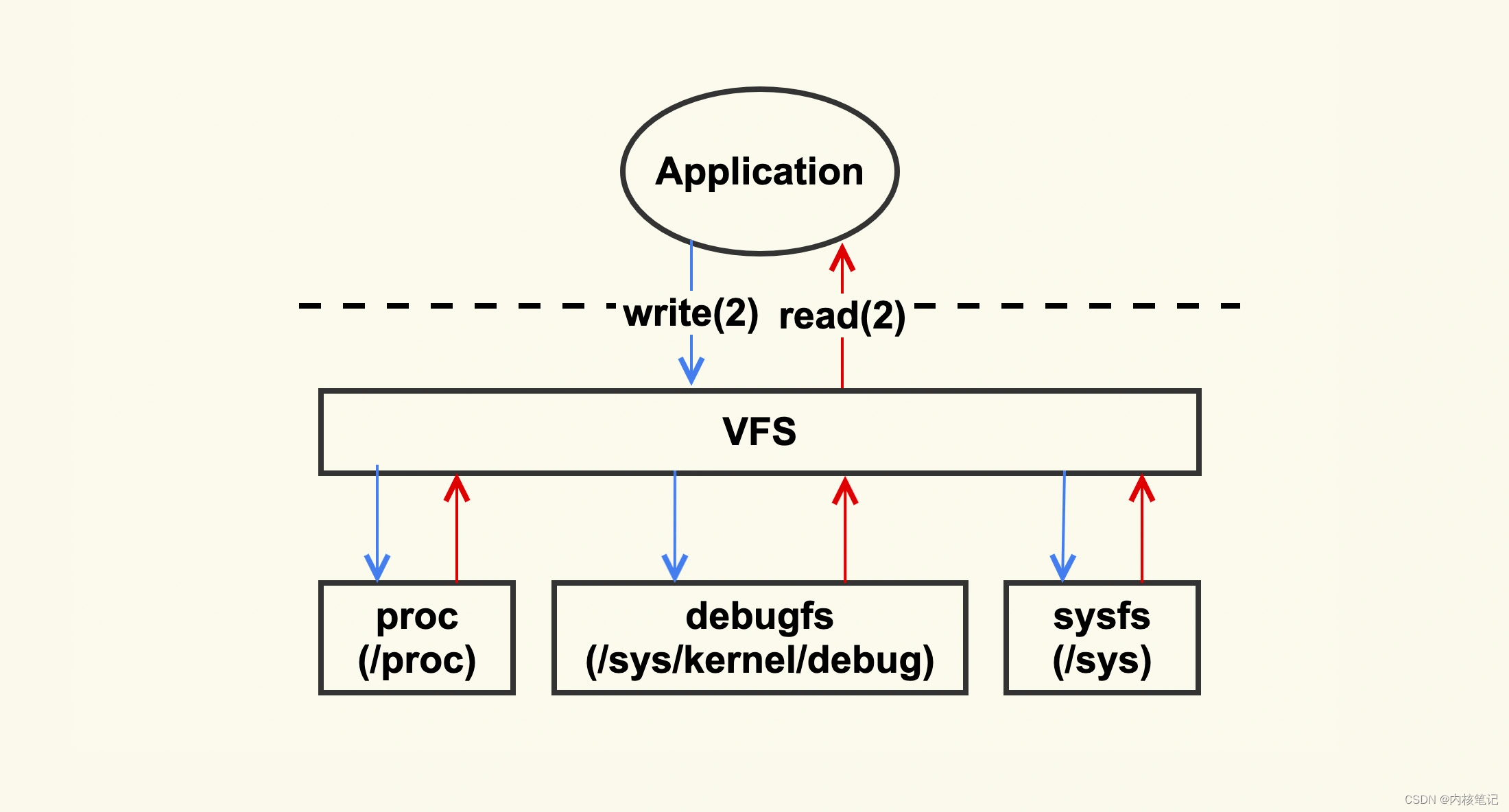
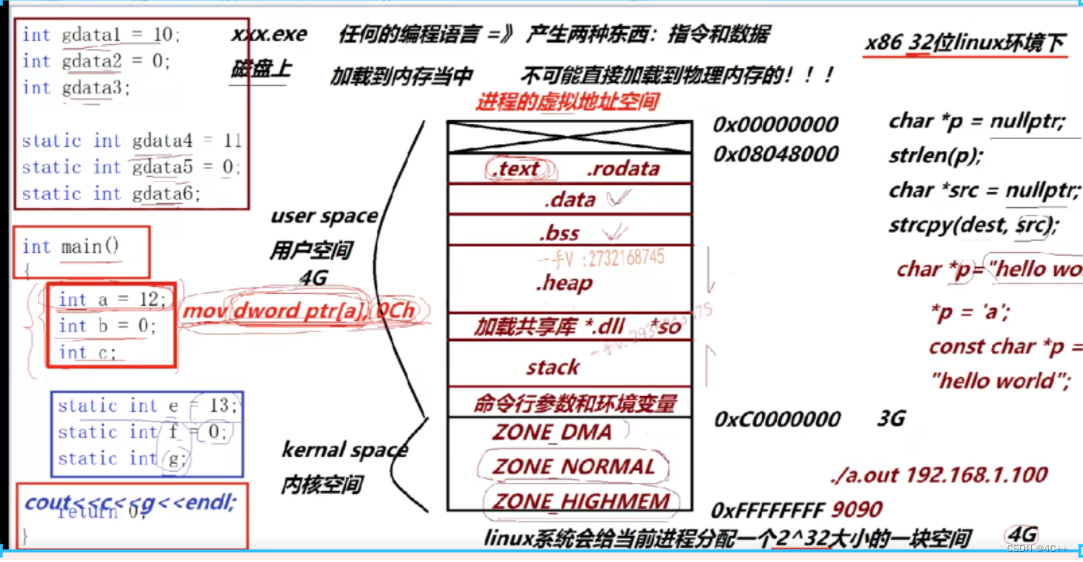
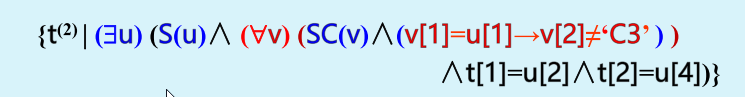以下内容来源于MOOC学习—原课程请见：数据库原理与应用
考研复习

概述

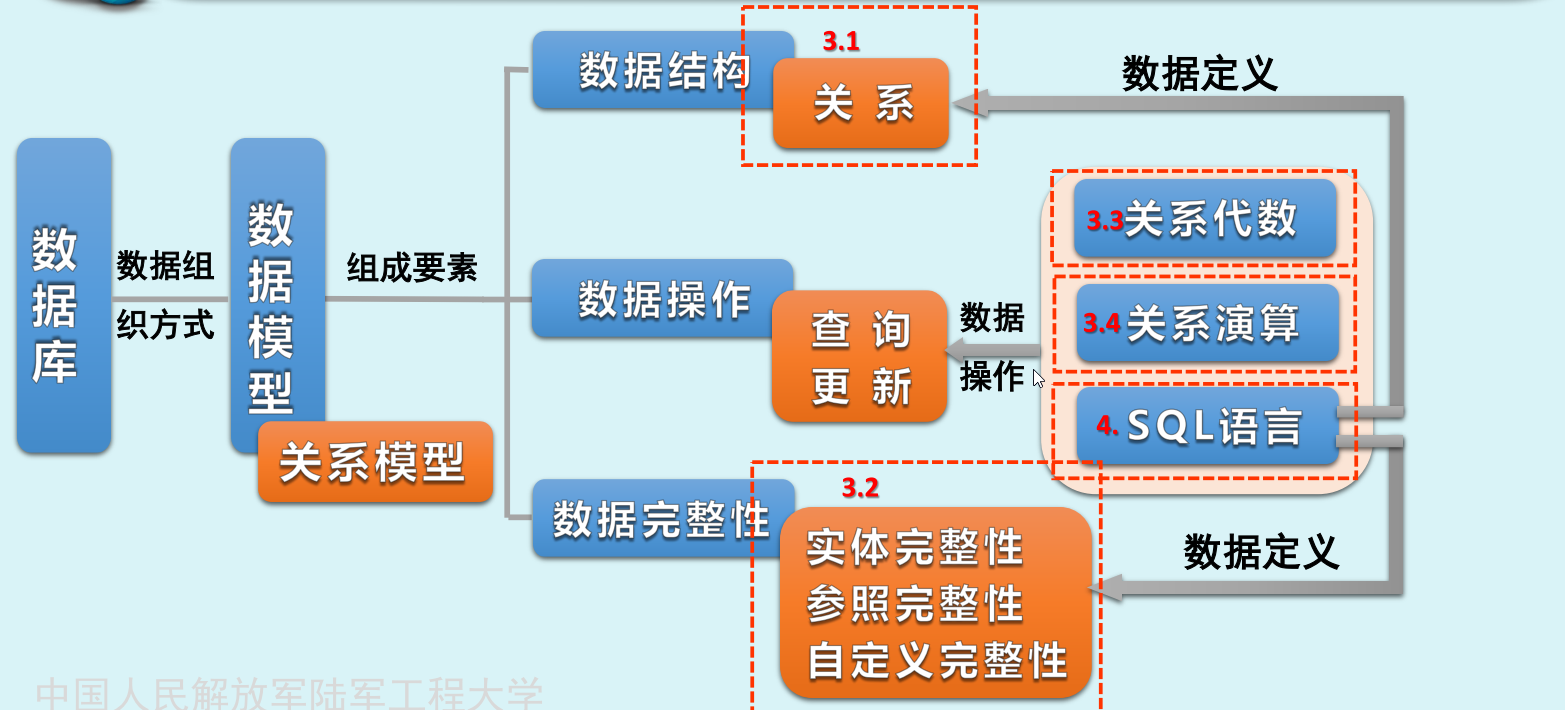
关系及关系模式

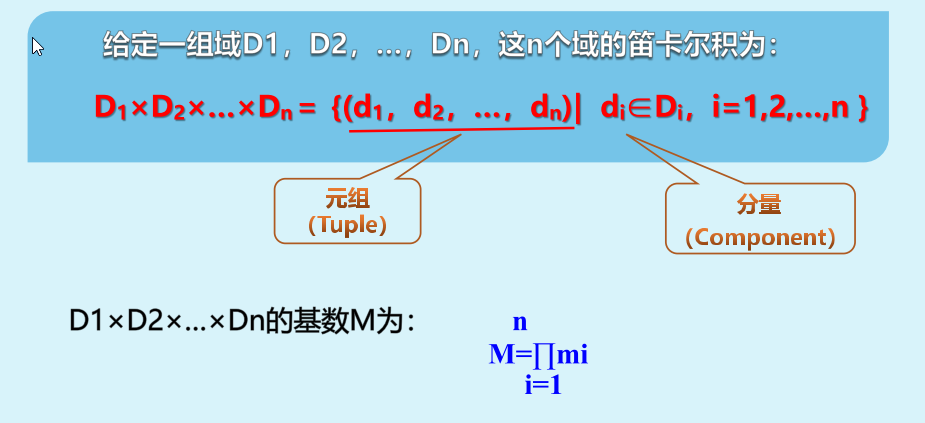
笛卡尔积

定义在一组域上的有序对的集合，

域是一组具有相同类型的集合，比如自然数，长度小于n的字符串结合等【比如int age】

从n个域的每个域里任取一个值，构成元素集合中的一个，【name取zhao，age取15，构成 zhao,15】

每一个元素称为一个n元祖 简称元祖，元祖中每个值称为分量【name:zhao,age:15即元组】

注意基数的计算

关系

日常生活：事物之间关系的描述，比如人的关系，电压电流

数学中：集合论里—关系本身也是一个集合，是具有某种联系的对象（序组）组合

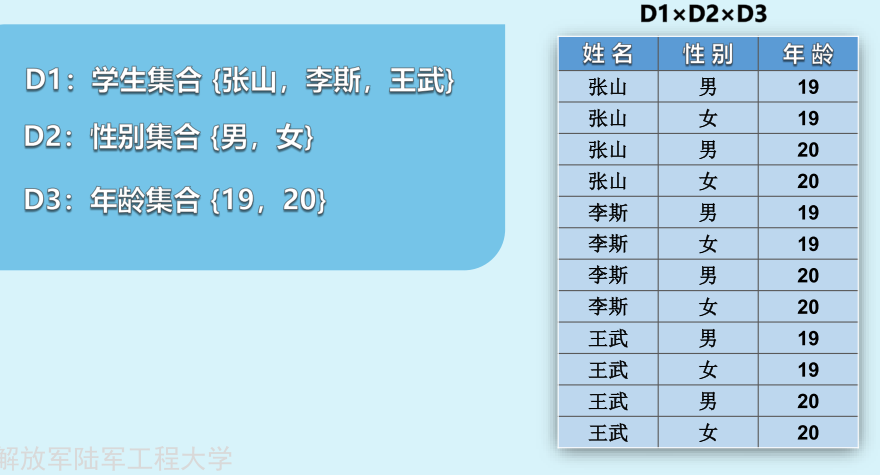
​ D1 D2 D3上的笛卡尔积共有12个元组（3x2x2），但是由于一个人只有一个姓名，许多元组[一个元祖表示一个学生的姓名，性别，年龄]并没有意义，因此其中有意义的即关系

​ 从笛卡尔积中取出一定语义的元祖，构成这N个域上的一个关系，或者说关系是笛卡尔积上的某个有意义的自子集R(D1,D2,…Dn)

同时要满足：

1. 域要求满足第一范式-------域都是原子数据的集合

• 属性值不能再细化分成多个

• 属性也不能是多值属性，

2. DOM

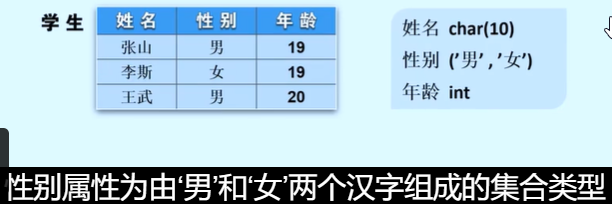
3. 属性间的依赖关系

比如张山的性别？是男----反应姓名和性别的依赖；数据内在的性质

关系模式简化

关系名和属性名的集合 R(A1,A2,…An)； 比如指导（指导老师，专业，学生姓名）

关系实例

给定关系下 某一时刻的元祖的集合（二维表），时刻变化的数据；理解为具体数据库中表值

关系模式

是关系的型的描述，静态，稳定的；比如指导（指导老师，专业，学生姓名）

关系数据库

略，参考第二章补充

概念分析

集合中的关系：关系可以是一个无限集合 • 关系中每个元组是“序组”

关系模型的关系：关系必须是有限集合 • 为关系的每个属性附加一个属性名(age)取消分量的有序性

如果不附加属性名，那么关系模式语义相同，可以表达同一个关系，如下

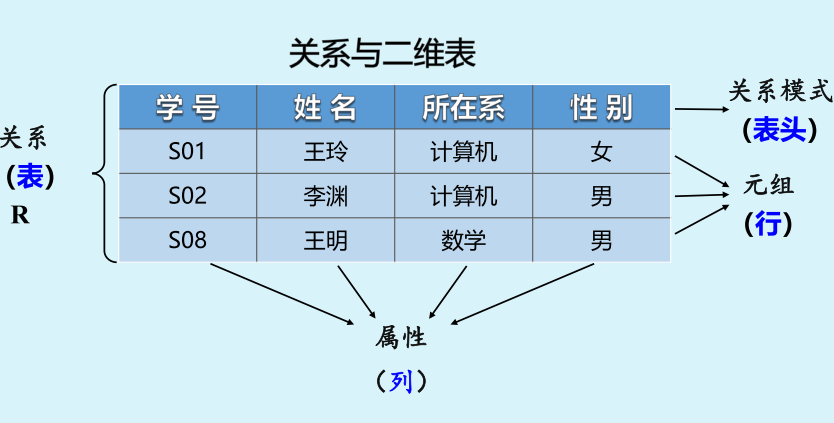
参考第二章

	关系	表
	关系是n个域上的一个n元组的集合	表是关系的“二维”呈现
	关系中属性的次序和元组的次序都是任意的	在表中各列从左到右是有序的，各行从上到下也是有序的
	关系中不能有相同的元组（行）[但是可以属性值可以相同，比如指导老师和学生都叫李亮]	在表中，可能包含重复的行

候选键，主键和外键

候选键：能唯一 标识一个元祖的 最小属性集

如果有多个候选键，可以选择一个作为主键

如果仅一个候选键，且候选键就是关系所有的属性，称为全键

包含候选键的属性集称为超键；

构成候选键的每个属性（候选键的每个属性）都是主属性，其他都是非主属性

外键：关系R的一个属性（集）F与关系S的主键KS对应，对应即取值相对应，称该属性（集）F是关系R的外键

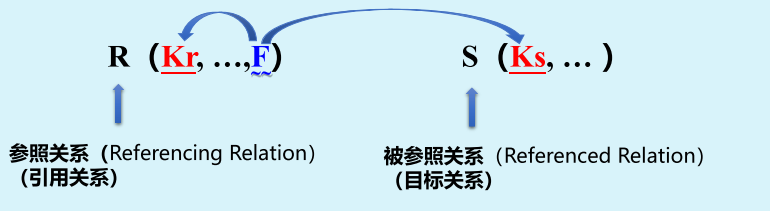
1. 外键不一定要与相应主键同名；如果属于不同的关系（表），往往取相同的名字
2. 外键与相应主键必须有相同的域，即属性值的数据类型要完全一致

例：在关系模式EMP（职工号，姓名，年龄，技能）中，假设职工号唯一，每个职工只能申报一项技能，则EMP表的主键是（ ）。

​ A.职工号 B.姓名，技能 C.技能 D.职工号，技能

正确答案：A你错选为D

完整性约束

实体完整性[主属性不能为空]

如果属性A是关系R（表R）的主属性，则A不能为空值（null）

参照完整性[外键完整]

该属性（集）F是关系R的外键

该属性（集）F取值只有两种：

• 取空值
• 等于某个KS 的值

用户自定义的完整性

• 属性类型约束：年龄取整数

• 属性值的范围：成绩

• 同一关系的不同元祖进行约束：不允许出现姓名相同的人

• 同一关系的各种属性：工资=绩效+· 等等

关系代数

代数：操作运算符（±*/）+原子操作数

关系代数：基于一组以关系为惭怍对象的运算符+原子操作数（理解为一行数据）

传统集合运算【二目运算】：并、交、差，笛卡尔积

专门关系运算：投影、选择、连接、除

五种基本操作（可扩展得到其他）并、交、笛卡尔积、投影、选择

并∪、交∩、差－

相容关系：定义在一组相同域上的不同关系：

• 关系名可以不同，属性名也可以不同，但是**必须具有相同个数的属性**

• 两个关系（表）具有相同的目（列），且相应属性取值属于同一个域

并、交、差都属于相容关系

并：用关系代数的基本运算表示为R∪S={t|t∈R∨t∈S} 重复元组舍弃

差：以用关系代数的基本运算表示为R-S={t|t∈R∨t∉S} R-S表示在R中但是不在S中

交：用关系代数的基本运算表示为R∩S={t|t∈R^t∈S}=R-(R-S)

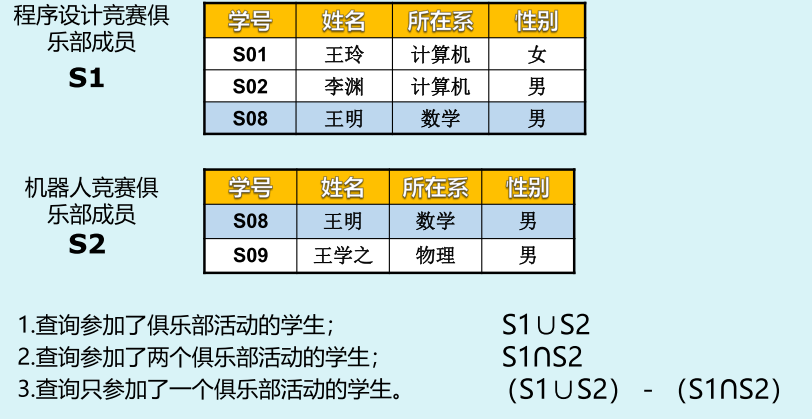
例：将王玲的所在系改为数学系：

（S1-{(‘S01’ ‘王玲’ ‘’ ‘女’)})∪{(‘S01’ ‘王玲’ ‘数学’ ‘女’)}

投影π、选择σ

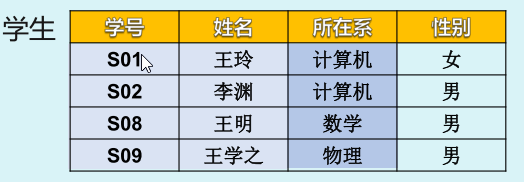
投影：一元的，对属性[列]进行操作的运算；从关系中选取若干属性列重新组合新的关系

1. 查询所有学生的学号、姓名：π学号,姓名(学生)

选择：一元的，对元祖[行]进行操作的运算；从关系中选取满足给定条件的元祖

1. 选择所在系属性值为‘计算机’的元组：σ所在系=“计算机”(学生)

2. 查询计算系学生的姓名：π姓名(σ所在系=“计算机”(学生))

3. 查询2000-01-01以后出生的学生姓名:π姓名(σ出生时间>“2020-01-01”(学生))

4. 查询没选修课程编号为“C02”的学生学号:π学号(选课)-π学号(σ课程编号=“c02”(选课))

σF®的R：由基本逻辑表达式组成：其中运算符包括< > = 小于等于 大于等于 不等于 与或非

注释：一元：对一个关系进行操作

广义笛卡尔积R x S

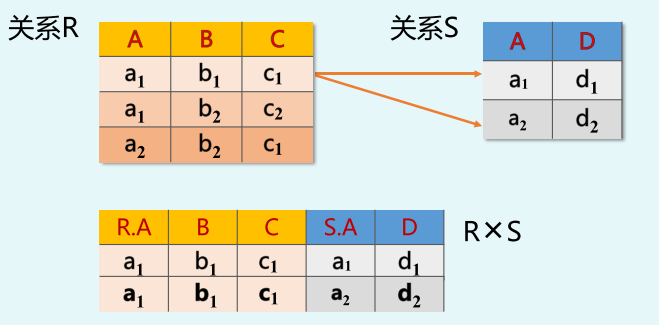
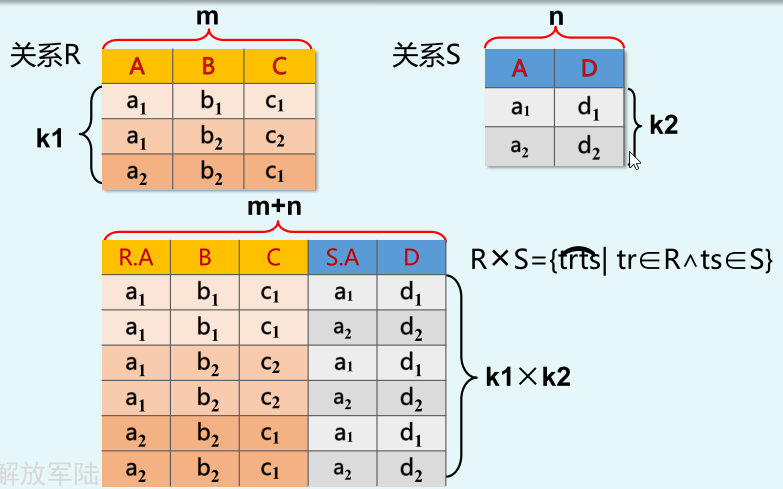
R是m目，S是n目，RxS得到的m+n目，共有k1*k2个元祖

如果有重名属性，则进行更名

连接∞

​ R ⋈AθB S=σF(R×S) R⋈A𝛉B S = σR.A𝛉S.B (RXS) 【R.A𝛉S.B即条件】

​ A和B分别是R和S上列数相等且可以比较的属性组（列），θ是运算符，如＞＜，连接运算时从R和S的笛卡尔积上选取R关系在A属性组的值 与 S关系中B 的属性值 满足运算关系的元祖

​ 可以理解为在笛卡尔积运算的基础上，进行选择运算就是连接

连接和自然连接

等值连接：比较的关系必须是A=B，即选取A和B的值相等的元祖

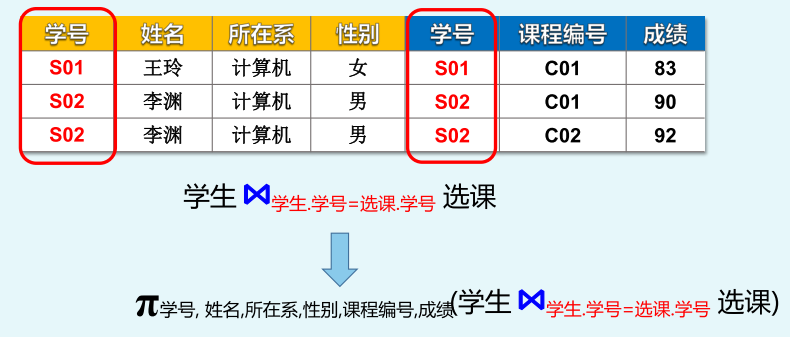
自然连接：必须是同名的属性组，在结果中去除重复的列

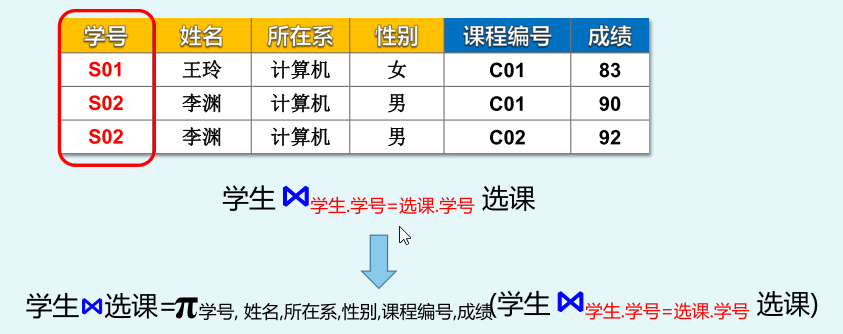
在自然连接时【例如S08没有对应的】，不能和另一个关系的任何元组进行连接，称为悬浮元组

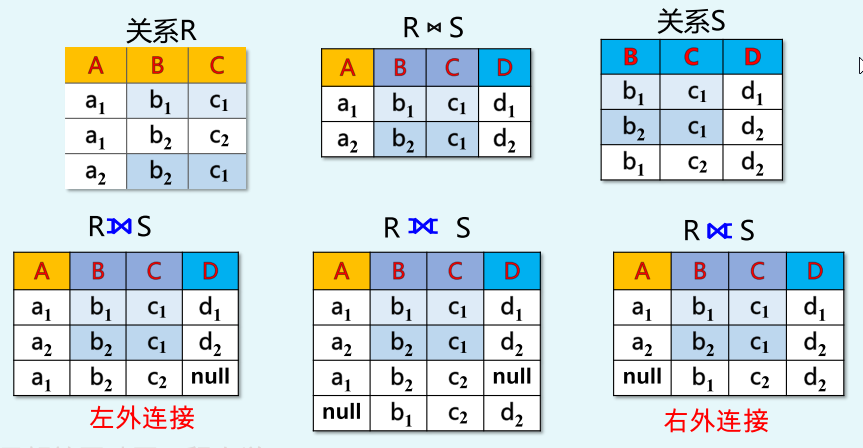
外连接

自然连接后：

1.如果把左右连接的悬浮元组都保存下来就是完全外连接

2.如果把左连接的悬浮元组保存下来就是左外连接

3.如果把右连接的悬浮元组保存下来就是右外连接

左（右）外连接：得到R和S的连接表后，查看左（右）表的剩余元素，补充上，无属性值赋予NULL

举例：学校数据库中有学生和宿舍两个关系：

​ 学生（学号，姓名） 宿舍（楼名，房间号，床位号，学号）

假设有的学生不住宿，床位也可能空闲。如果要列出所有学生住宿和宿舍分配的情况，包括没有住宿的学生和空闲的床位，则应执行–全外连接

重命名ρ

关系（表）的自身连接 或者具有相同属性时的笛卡尔积计算 时，

有相同的字段需要区分，则对表进行重命名 ρs® s就是表的名字

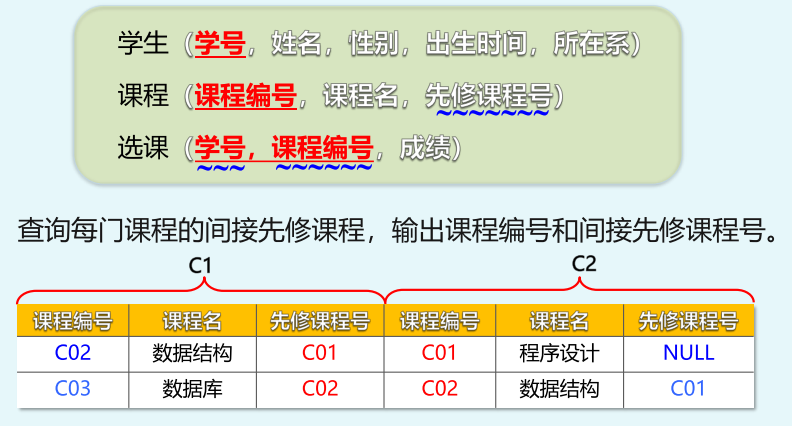
除÷

前提：

• 前提：R中的属性包含S中的所有属性
• R÷S的属性由R中那些不出现在S中的属性组X所组成
• R÷S的结果T元祖 + S 的元祖 都在R中

---

上例子：查询选修全部课程的学生

​ R选课(学号，姓名，课程名) S课程(课程名)

​ π姓名® X S 得到的是假设每名学生选择了所有课程

①π姓名® X S - R 得到没有选修全部课程的 姓名+课程

②π姓名®-π姓名(π姓名® X S - R)得到结果

R÷S=π姓名®-π姓名(π姓名® X S - R)

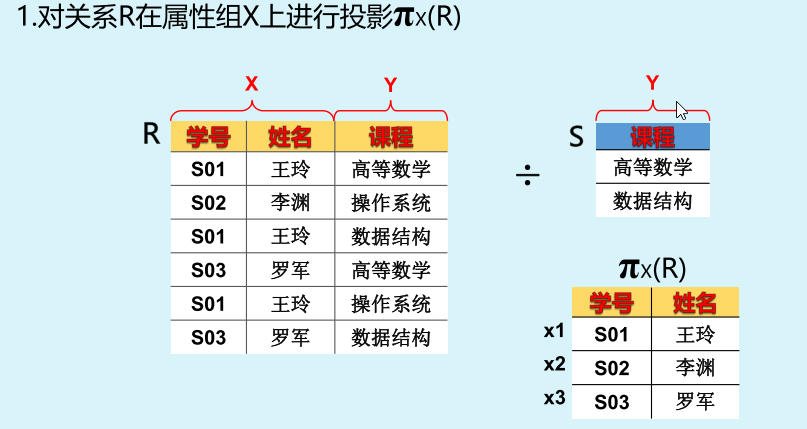
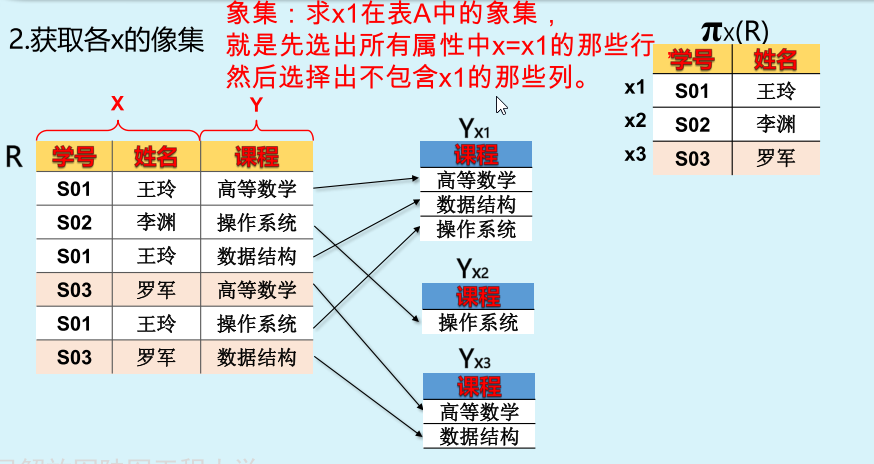
像集：本质上是一次选择行的运算和一次选择列的运算。

求x1在表A中的象集，就是先选出所有x属性中x=x1的那些行，然后选择出不包含x1的那些列。

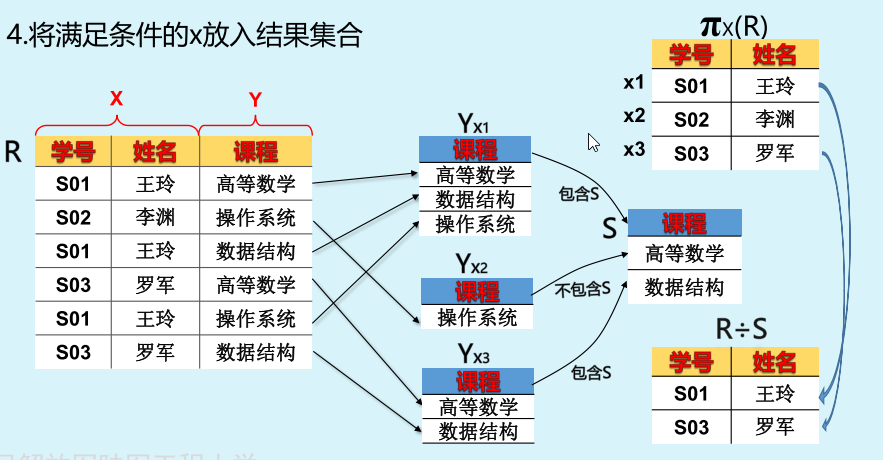
检查各个X在Y上的像集Yxi是否包含S

举例：

查询选修了全部课程的学生学号

​ 第一种方法： 选课÷ 课程编号(课程) ×[错误，不符合除运算的前提]

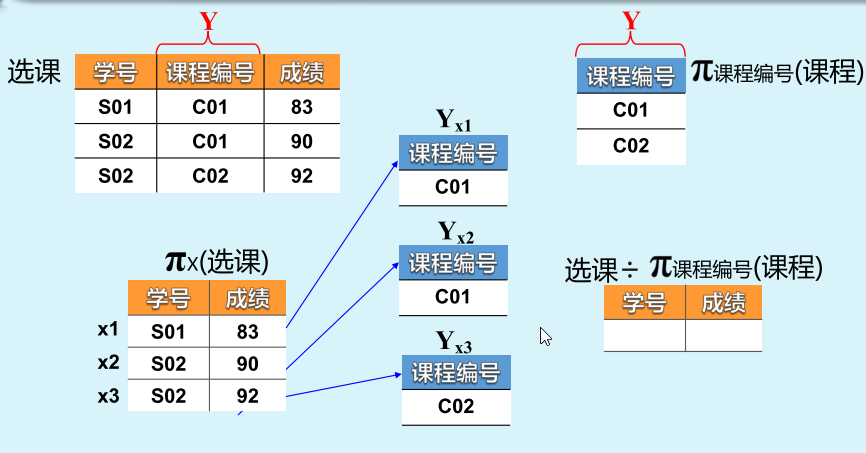
​ 第二种方法： π学号，课程编号(选课)÷ 课程编号(课程)√

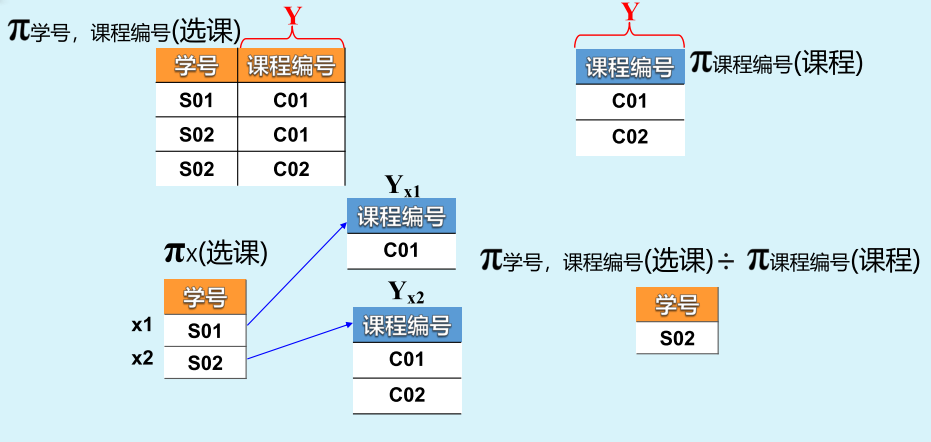
举例：

基于教学视频中的学生选课数据库，能正确查询出“数学系学生都学的课程的课程编号”的关系代数表达式是（ π学号,课程号(选课) ÷π学号(σ所在系=‘数学’(学生)) ）

基于教学视频中的学生选课数据库，能够正确查询“所有学生都选修的课程的课程编号”的关系代数表达式是（ π学号,课程号(选课) ÷π学号(学生) ）。

关系演算

1.将数理逻辑中的谓词演算推广到关系运算中，用谓词演算表达操作

2.关系是一个集合，因此可以用集合描述法建立谓词与关系之间的描述

3.用谓词表示关系，可用关系的谓词演算来表达关系的操作，把对关系的谓词演算的集合描述形式称为关系演算表达式

---

注：阅读以下内容：元组可以理解为关系（表）中一个数据，元组所有变量构成一个数组t[i]表示元组（数据）的第i个属性-------

在元组关系演算系统中，称 {t|Φ(t)} 为元组演算表达式。

其中 t 是元组变量， Φ(t) 为元组关系演算公式，简称公式。
它由原子公式和运算符组成。

原子公式有三类：

(1) R(t) R 是关系名， t 是元组变量。 R(t) 表示 t 是 R 中的元组。关系 R 可表示为： {t|R(t)}

(2) t[i] θ u[j]

​ θ 是算术比较运算符。 t[i] θ u[j] 表示断言 “ 元组 t 的第 i 个分量（属性）与元组 u 的第 j 个分量满足比较关系 θ ” 。例如， t[2] < u[3] 表示元组 t 的第 2 个分量小于元组 u 的第 3 个分量。

(3) t[i] θ c 或 c θ t[i]
这里 c 是常量，该公式表示 “t 的第 i 个分量与常量 C 满足比较关系 θ” 。例如： t[4]=3 表示元组 t 的第 4 个分量等于 3 。

​ 在关系演算中定义了 “ 自由元组变量 ” 和 “ 约束元组变量 ” 的概念。这些概念和谓词演算中的概念完全一样。若公式中的一个元组变量前有 “ 全称量词 ” 或 “ 存在量词 ” ，则称该变量为约束元组变量，否则称自由元组变量。

公式可以递归定义如下：

(l) 每个原子公式是公式。

(2) 如果 Φ 1 和 Φ 2 是公式，则 Φ 1 ∧ Φ 2 、 Φ 1 ∨ Φ 2 、 ﹁ Φ1 也是公式。分别表示：

① 如果 Φ 1 和 Φ 2 同时为真。则 Φ 1 ∧ Φ 2 才为真，否则为假；

② 如果 Φ 1 和 Φ 2 中至少一个为真，则 Φ 1 ∨ Φ 2 为真， Φ 1 和 Φ 2 同时为假 才为假；

③ 如果 Φ 1 真，则 ﹁ Φ 1 为假。

(3) 若 Φ 是公式，则 ∃ t(Φ) 也是公式。其中符号 ∃ 是存在量词符号， ∃ t(Φ) 表示：
若有一个 t 使 Φ 为真，则 ∃ t(Φ) 为真，否则 ∃ t(Φ) 为假。

(4) 若 Φ 是公式，则 ∀ t( Φ ) 也是公式。其中符号 ∀ 是全称量词符号， ∀ t( Φ ) 表示：
如果对所有 t ，都使 Φ 为真，则 ∀ t( Φ ) 必为真，否则 ∀ t( Φ ) 为假。

(5) 在元组演算公式中，各种运算符的优先次序为：
① 算术比较运算符最高；
② 量词次之，且 ∃ 的优先级高于 ∀ 的优先级；
③ 逻辑运算符最低，且 ﹁ 的优先级高于 ∧ 的优先级， ∧ 的优先级高于 ∨ 的优先级；
④ 加括号时，括号中运算符优先，同一括号内的运算符之优先级遵循 ①②③ 各项。
(6) 有限次地使用上述五条规则得到的公式是元组关系演算公式，其他公式不是元组关系演算公式。

---

关系演算和关系代数在表达能力上是等价的 ，体现在五种基本操作

一个元组演算表达式 {t|Φ(t)} 表示了使 Φ(t) 为真的元组集合。
关系代数的运算均可以用关系演算表达式来表示 ( 反之亦然 ) 。下面用关系演算表达式来表示五种基本运算：

(1) 并 R ∪ S={t|R(t) ∨ S(t)}

(2) 差 R － S={t|R(t) ∧ ﹁ S(t)}

(3) 笛卡尔积 R×S={t (n+m) |( ∃ u (n) )( ∃ v (m) )(R(u) ∧ S(v) ∧ t[1]=u[1] ∧ … ∧ t[n]=u[n] ∧ t[n+1]=v[1] ∧ … ∧ t[n+m]=v[m])}

​ 注： t (n+m) 表示 t 有目数 (n+m)

(4) 投影 π t1,t2,…,tk ®={t (k) |( ∃ u )(R(u) ∧ t[1]=u[i1] ∧ …t[k]=u[ik] )}

(5) 选择 σ F ®={t|R(t ∧ F}

​ 注： F 是公式。 F 用 t[i] 代替 运 算 对 象 i 得到的等价公式。

1.

4.

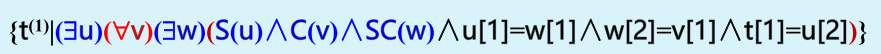
5.