目录

初始化

插入

查询

合并集合 

连通块中点的数量 

堆排序 

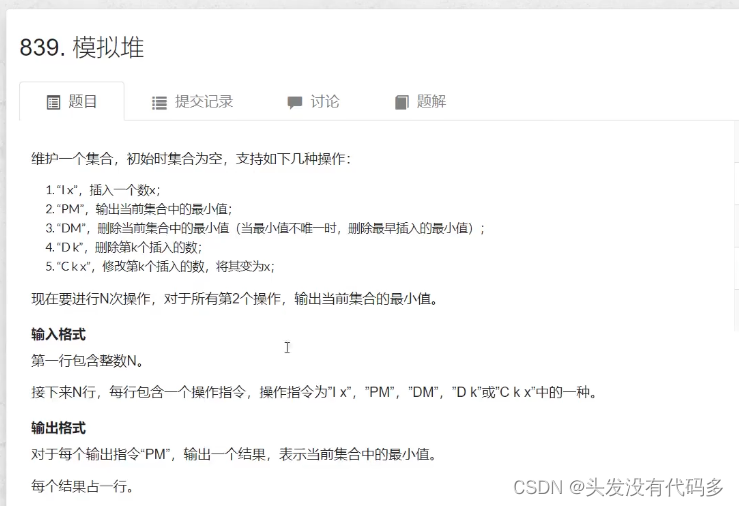
 模拟堆

---

 

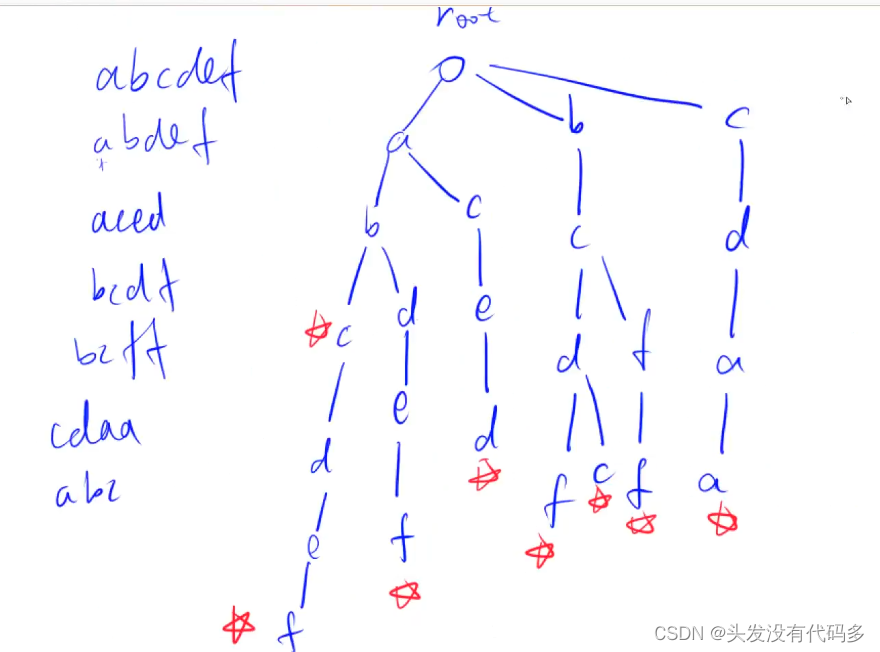
Trie树是用来快速存储和查找字符串集合的数据结构

 

#include<iostream>
using namespace std;
const int N = 100010;
int son[N][26];//本题为小写因为字母，每个节点最多有26个子节点,所以是N,26
int cnt[N];//以当前节点结尾的字符有多少个
int idx;//当前所用到的下标，下标是0的点，即使根节点，又是空节点
char str[N];
void insert(char str[])
{
	int p = 0;
	for (int i = 0; str[i]; i++)//str结尾是\0，我们这里用str[i]判断是否走到了结尾
	{
		int u = str[i] - 'a';//当前字母对应的子节点编号，把a-z，映射成0-25
		if (!son[p][u]) son[p][u] = ++idx;//如果当前p节点不存在u当前所代表的字母，我们就把它创建出来
		p = son[p][u];//走到下一个点
	}
	cnt[p]++;// 结束的时候 p 指向的点 对应 插入字符串的最后一个字符，表示以该点结尾的单词数量多了一个
}
int query(char str[])//查询操作
{
	int p = 0;
	for (int i = 0; str[i]; ++i)
	{
		int u = str[i] - 'a';
		if (!son[p][u])//如果不存在该节点
			return 0;
		p = son[p][u];///否则的话就走到下一个点
	}
	return cnt[p];
}
int main()
{
	int n;
	scanf("%d", &n);
	while (n--)
	{
		char op[2];//存储操作类型
		scanf("%s%s", op, str);
		if (op[0] == 'I')
		{
			insert(str);
		}
		else
			printf("%d\n",query(str));
	}
	return 0;
}

Trie(字典树）是一种用于实现字符串快速检索的多叉树结构。Trie 的每个节点都拥有若干个字符指针，若在插入或检索字符串时扫描到一个字符 c，就沿着当前节点的 c 字符指针，走向该指针指向的节点。

Trie树可以 高效 支持 两个操作：

• 存储字符串集合
• 查询字符串集合

有一个 经验：凡是用到Trie树的题目，一般来说给出的字符串要么全是小写字母，要么全是大写字母，要么都是数字，要么全是0或1，总之字母类型不是很多。

下面来看看它是如何高效存储字符串的：

初始化

一棵空Trie树 仅包含一个根节点，该点的字符指针 均指向空。

插入

（1）过程分析

当需要 插入一个字符串S 时，我们令一个指针Р起初指向根节点。然后，依次扫描S中的每个字符c:

• 1.若P的c字符指针 指向一个已经存在的节点Q，则 令P= Q。
• 2.若P的c字符指针 指向空，则 新建一个节点Q，令P的c字符指针 指向Q，然后 令P=Q。

当s中的字符 扫描完毕时，在当前节点P上 标记它是一个字符串的末尾。

下图展示了 向Trie树中插入字符串过程，每插入一个字符串 都会标记一次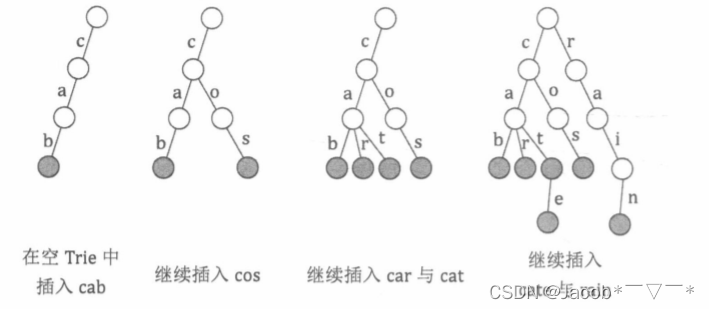

在上图所示的例子中，需要插入和检索的字符串都由小写字母构成，所以Trie 的每个节点具有26个字符指针，分别为a到 z。

上图展示了在一棵空Trie中依次插入“cab"、“cos"、"car"、“cat”、" cate” 和 “rain” 后的 Trie 的形态，灰色 标记了 单词的末尾节点。

可以看出在Trie 中，字符数据都体现在树的边（指针）上，树的节点仅保存一些额外信息，例如 单词结尾标记等。

（2）空间复杂度

O(NC)，其中 N是节点个数（即我们想要存储的字符串的最大长度），C是字符集的大小（如：26个字母则 C = 26，Trie树中 每个节点最多向外生26条边）。

（3）时间复杂度

与树的高度成正相关

（4）代码片段

const int N = 1e7+10;
inr son[N][26]; //存储Trie树中每个点所有儿子
int cnt[N]; //存储以当前这个节点结尾的单词有多少个
int idx; //当前用到了哪个下标，下标是0的节点既是根节点，又是空节点

void insert(string s)
{
    int p = 0; //从根节点开始
    for(int i=0; i<s.size(); ++i) //从前往后遍历所插字符串的每个字符
    {
        int u = s[i] - 'a'; //每次将遍历到的当前字符对应的子节点编号求出（将小写字母 a~z 映射成 0~25）
        if(!son[p][u]) son[p][u] = ++idx; //如果当前节点 p 不存在 u 这个儿子，就创建出来
        p = son[p][u]; //走到下一个点
    }
    cnt[p]++; //结束的时候 p 指向的点 对应 插入字符串的最后一个字符，表示以该点结尾的单词数量多了一个
}

查询

（1）过程分析

当需要 查询一个字符串S在Trie中是否存在 时，我们令一个指针Р起初指向根节点，然后依次扫描S中的每个字符c:

• 1.若P的c字符指针 指向空，则说明S没有被插入过Trie，结束查询。
• 2.若P的c字符指针 指向一个已经存在的节点Q，则 令P =Q。

当S中的字符 扫描完毕时，若当前节点Р 被标记为一个字符串的末尾，则说明S在Trie中 存在，否则 说明 s没有被插入过Trie。

（2）时间复杂度

与树的高度成正相关

（3）代码片段

int query(string s) //返回的值是字符串出现的次数
{
    int p=0; //从根节点开始
    for(int i=0; i<s.size(); ++i)
    {
        int u = s[i]-'a'; //每次将遍历到的当前字符对应的子节点编号求出（将小写字母 a~z 映射成 0~25）
        if(!son[p][u]) return 0; //如果当前节点 p 不存在 u 这个儿子，说明当前集合不存在这个单词，直接返回 0 即可
        p = son[p][u]; //否则的话就走到下一个点
    }
    return cnt[p]; //返回以 p 结尾的单词数量
}

合并集合 

 

 

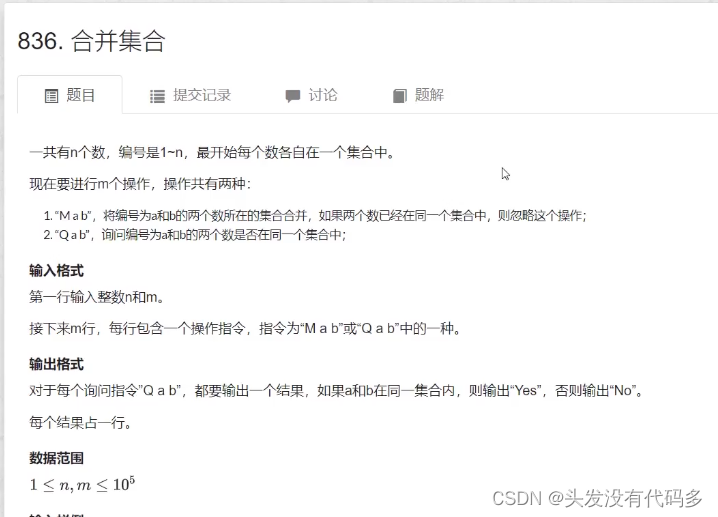
并查集可以在近乎O(1)的时间复杂度内支持这俩个操作 

  

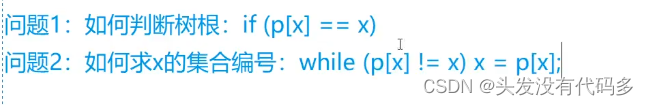
 合并：让一个树成为另一棵树的子树

#include<iostream>
using namespace std;
const int N = 100010;
int p[N];//存储每个元素的父节点,当p[i]=i时，i就是树根
int n,m;
int find(int x)//返回x所在集合的编号(返回x的祖宗节点)+路径压缩
{
	if (p[x] != x) p[x] = find(p[x]); 
	return p[x];
}
int main()
{
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= n; ++i)
	{
		p[i] = i;//先把所有p节点的值赋成自己
	}
	while (m--)
	{
		char op[2];
		int a, b;
		scanf("%s%d%d", op,&a,&b);
		if (op[0] == 'M')
		{
			p[find(a)] = find(b);//合并操作,让A的祖宗节点成为B祖宗节点的子节点

		}
		else//判断俩节点是不是在同一集合里
		{
			if (find(a) == find(b))
			{
				puts("Yes");
			}
			else
				puts("No");
		}
	}
	return 0;
}

 如何知道当前集合个数？

连通块中点的数量 

 

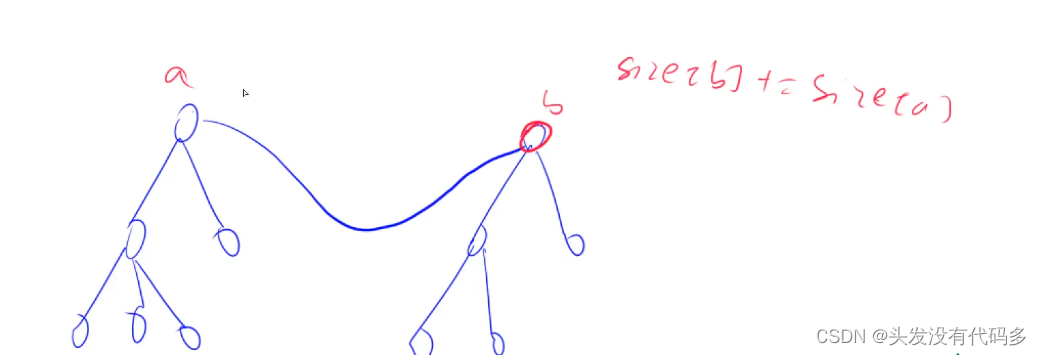
把a插到b里面，之后更新size[b]即可 

#include<iostream>
using namespace std;
const int N = 100010;
int p[N],SIZE[N];//存储每个元素的父节点,当p[i]=i时，i就是树根,size[N]表示每个集合里面点的数量，只有根节点的size有意义 
int n,m;
int find(int x)//返回x所在集合的编号(返回x的祖宗节点)+路径压缩
{
	if (p[x] != x) 
p[x] = find(p[x]); //起到路径压缩的作用
	return p[x];
}
int main()
{
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= n; ++i)
	{
		p[i] = i;//先把所有p节点的值赋成自己
		SIZE[i] = 1;//最开始每个集合里面只有一个点
	}
	while (m--)
	{
		char op[5];
		int a, b;
		scanf("%s", op);
		if (op[0] == 'C')
		{
			scanf("%d%d", &a, &b);
			if (find(a) == find(b))
				continue;
			SIZE[find(b)] += SIZE[find(a)];
			p[find(a)] = find(b);//合并操作,让b的祖宗节点成为a祖宗节点的子节点

		}
		else if (op[1] == '1')//询问是否在俩个集合当中Q1
		{
			scanf("%d%d", &a, &b);
			if (find(a) == find(b))
				puts("Yes");
			else
				puts("No");
		}
		else//某集合点中的数量
		{
			scanf("%d", &a);
			printf("%d\n", SIZE[find(a)]);
		}
	}
	return 0;
}

堆排序 

  

 

 

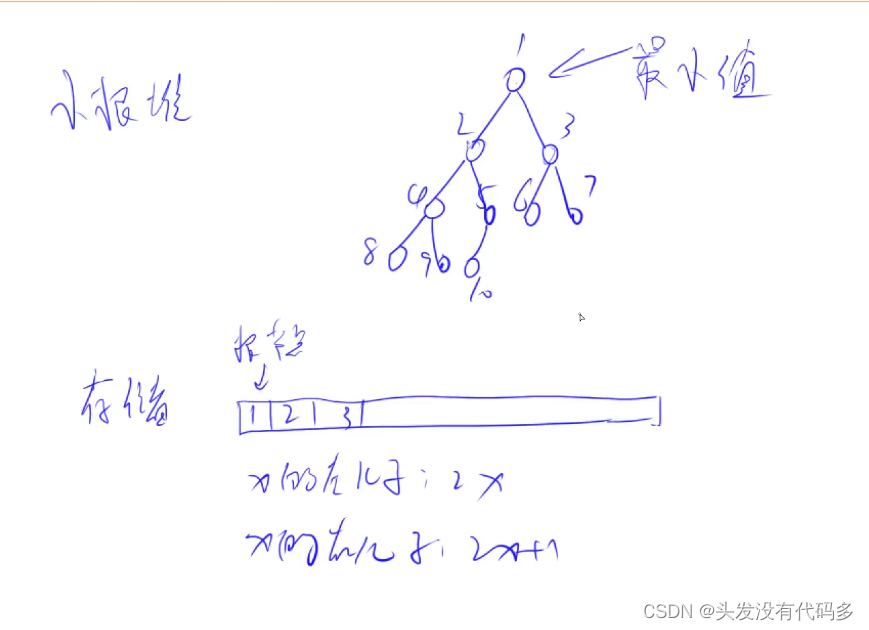
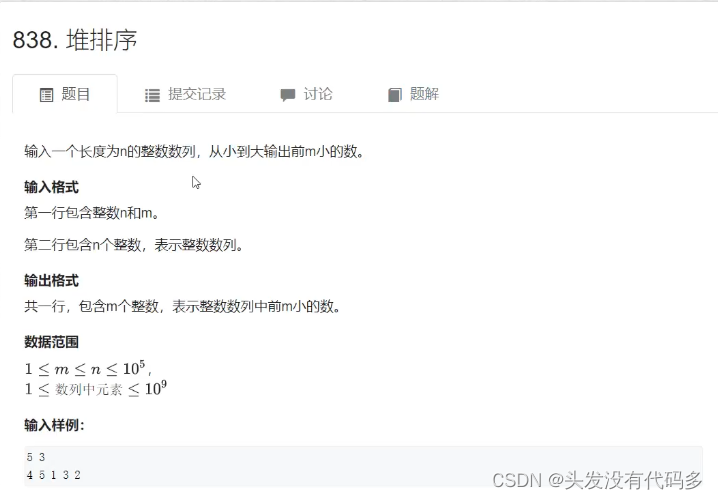
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 100010;
int n, m;
int h[N], SIZE;//size表示堆中当前有多少个元素
void down(int u)
{
	int t = u;//t表示左右儿子和父节点中的最小值
	if (u * 2 <= SIZE&& h[u * 2] < h[t]) t = u * 2;//如果数据在范围内，而且左儿子小于最小值，则t就是左儿子
	if (u * 2 + 1 <= SIZE && h[t] > h[u * 2 - 1]) t = u * 2 - 1;//右儿子
	if (u != t)//如果U不等于t，说明根节点就不是最小值，我们把最小值和根节点换一下即可
	{
		swap(h[u], h[t]);
		down(t);
	}

}
int main()
{
	scanf("%d%d", &n,&m);
	for (int i = 1; i <= n; ++i) scanf("%d", &h[i]);
	SIZE = n;
	for (int i = n / 2; i; i--)
	{
		down(i);
	}//从n/2开始建堆，会优化时间复杂度到O（N）
	while (m--)
	{
		printf("%d", h[1]);//打印堆顶元素
		//删除堆顶元素
		h[1] = h[SIZE];
		SIZE--;
		down(1);
	}
	return 0;
}

up操作 

void up(int u)
{
	while (u / 2 && h[u / 2] > h[u])//只要有父节点，而且当前节点大于父节点，就换上去
	{
		swap(h[u / 2], h[u]);
		u /= 2;
	}
}

 模拟堆