🐱作者：一只大喵咪1201
🐱专栏：《C++学习》
🔥格言：你只管努力，剩下的交给时间！

🍉map和set中的红黑树

我们在学习红黑树的时候，实现的是KV模型，节点中存放的是键值对pair。

• 而set中的节点只存放一个key值，map中的节点存放的是键值对。
• 但是map和set却使用的是同一颗红黑树。

这到底是怎么实现的呢？怎么做到一会儿是键值，一会又是键值对的呢？

我们来看一下STL库中是如何实现的：

• map和set中都既有key值，又有数据类型，map中的数据类型是键值对pair<const Key, T>，而set中的数据类型也是key值。
• STL模板中，红黑树中的数据类型只有一个。

无论是map还是set，底层封装的都是红黑树，区别在于给红黑树实例化的是什么类型的模板参数。

• map给红黑树传的模板参数是键值对pair<const Key, T>。
• set给红黑树传的模板参数是键值Key。

对于红黑树而言，它是不知道接收到的第二个模板参数value是什么类型的，它只能推演。

所以set对应的红黑树中的数据类型就是一个key值，而map对应的红黑树中的数据类型就是一个键值对。

接下来就是对我们实现的红黑树进行改造：

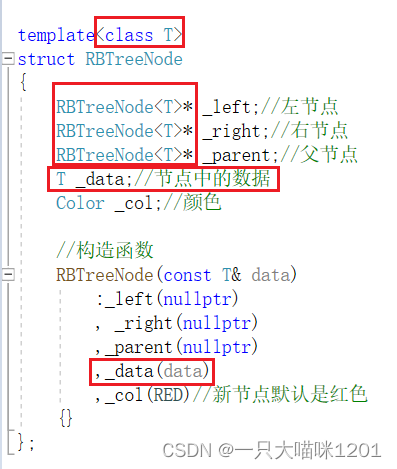
首先就是对节点进行改造，将原本的KV键值对数据类型改成T，像STL中一样，只有一个，让编译器自己去推演这个数据类型是key值还是键值对。

红黑树中也不再用键值对去构建新节点，而是使用那一个数据类型T。

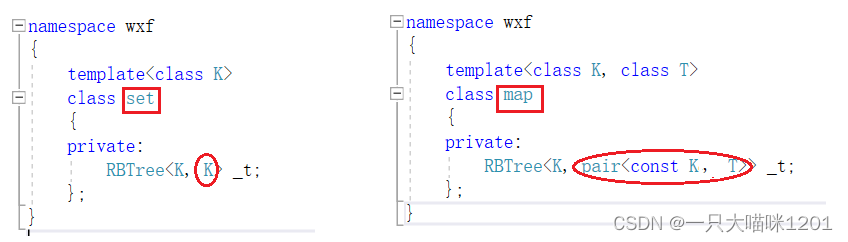
• set中，向红黑树传的模板参数是<K,K>，第二个K传给节点，作为节点是数据类型。
• map中，向红黑树传的模板参数是<K,pair<const K,T>>键值对，第二个参数键值对pair<const K, T>传给节点，作为节点的数据类型。

现在有一个问题，给红黑树传模板参数时，第一个参数K类型的作用是什么？节点中存放的数据第二个参数。

• 对于insert来说，set和map中都可以不要第一个参数K，因为第二个参数中就有K，可以用来比较。
• 但是对于find接口来说，它需要的只是K。
• set中第二个参数也是K，所以第一个K也可以省略。
• map中第二个参数是一个键值对，如果省略了第一K后，红黑树中只有一个键值对类型，在使用find的时候，无法确定拿到first的数据类型，此时就需要第一个模板参数K来确定find的类型了。

虽然set中可以不需要第一个模板参数K，但是map不可以，因它两使用的一个红黑树，所以为了统一，第一个模板参数K不能省略。

🍌set中的键值和map中的键值

站在红黑树的角度，并不知道它接收到的模板参数value是来自set中的键值还是map中的键值对。

在插入节点进行比较时：

• set：cur->data 与 data进行比较，插入节点中的key值直接和树中的key值比较大小，决定插入左还是右即可。
• map：cur->data.first 与 data.first进行比较，插入节点中的键值对的first和树种键值对的first比较，决定插入左还是右。

既然使用的是模板，是泛型编程，那么在比较处到底该写成map和set中的哪种比较方式呢？要知道set中的data不是键值对，是没有first的，而map中的data直接比较又不符合我们的要求。

pair提供的比较方式，first和second是都要看的：

• 当first不相等时first的比较结果就是最终结果。
• 当first相等时，要再看second的比较结果。

而红黑书中新节点和书中节点比较只要看key值，也就是键值对中的first，而不看second。

此时我们也不能自己重新定义键值对的比较方式，因为人家库中已经有了，我们无法再重载一个函数名，返回值，参数都相同的比较方式。

为了能够在红黑树中使用统一的比较方式，这里采用仿函数的方式：

在set和map中各定义一个仿函数，专门用来获取key值的，并且将这个仿函数当作模板参数传给红黑树。

• set中存放的数据本身就是key，所以获取key时有点多此一举，但是为了和红黑树的结构以及map的结构统一，也需要写一个。
• map中存放的数据是键值对，所以仿函数返回的是键值对中的first，依次来获取到key值。

• 在插入函数inset中，创建仿函数对象koft。
• 在需要进行键值key比较的位置，使用仿函数koft获取键值进行比较，然后决定插入左边函数右边。

使用仿函数的方法，压根就不用关心比较的是键值还是键值对，因为set和map都会给红黑树传它自己获取键值的仿函数，最终比较的都是键值。

• set和map中的插入直接复用红黑树中的插入即可。
• 但是set中插入的是一个键值，而map中插入的是一个键值对。

使用仿函数去取键值这一思路非常值得借鉴。

🍉红黑树的迭代器实现

map和set的迭代器可以参考list的迭代器，红黑树也是通过指针来链接的。

template <class T>
struct _RBTreeIterator
{
	typedef RBTreeNode<T> Node;
	typedef _RBTreeIterator<T> Self;
	Node* _node;
	//构造函数
	_RBTreeIterator(Node* node)
		:_node(node)
	{}
};

最基本的迭代如上面所示代码，迭代器中只有一个成员变量，那就是节点node。

下面就是逐渐完善迭代器支持的功能了，比如解引用，++，–等操作。

解引用和箭头：

这里和链表是一样的，就不再详细讲解了。

• 解引用返回的是节点中的数据data，箭头返回的是节点中数据的data的地址。

🍌迭代器++

set和map迭代器的++按照中序遍历的顺序进行加加的。所以要时刻铭记中序遍历的顺序：左子树 根 右子树

右子树存在：

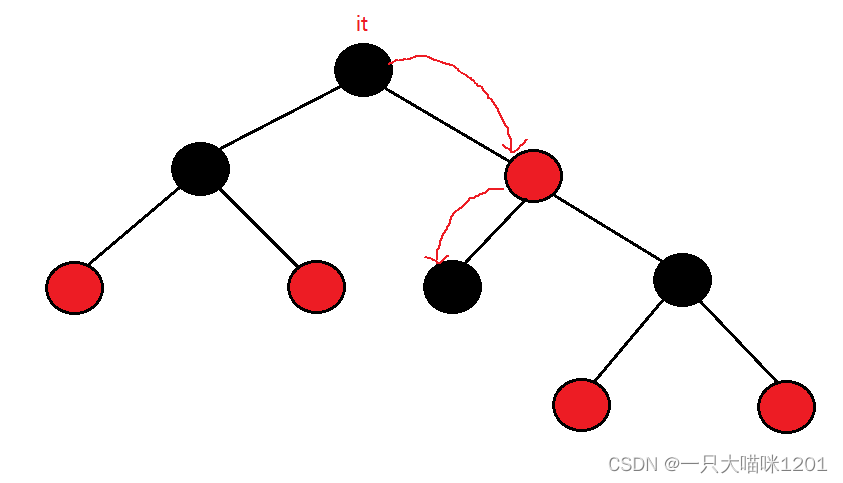
假设现在it在根节点，如上图所示。

• 当++it以后，it指向的是右子树中的最左节点，如上图所示。

//++it
	Self& operator++()
	{
		//右子树存在
		if (_node->_right)
		{
			//寻找右子树中的最左节点
			Node* MinLeft = _node->_right;
			while (MinLeft->_left)
			{
				MinLeft = MinLeft->_left;
			}
			_node = MinLeft;//找到最左边的最小节点
		}
		return *this;
	}

• 将当前it指向节点的有子节点开始，一直寻找最左节点。
• 找到后，让it指向最左节点。

右子树不存在：

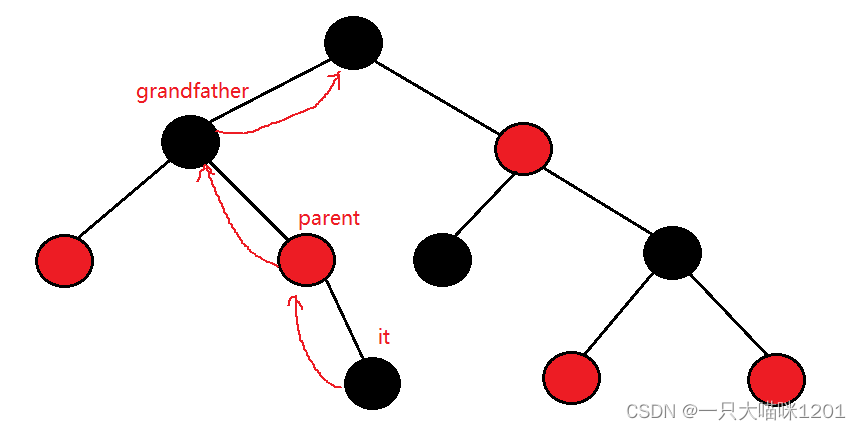
it处于上图所示位置，位于子树的最右边，当++it后，it会指向哪呢？it的右子树为空，肯定不能像上面那样找右子树最左边的节点。

• it是parent的右子树，说明父节点parent已经被访问过了，所以还需要继续向上走。
• parent又是grandfather的右子树，说明祖父节点grandfather也被访问过了，所以还需要继续向上走。
• grandfather是它父节点的左子树，按照中序遍历的顺序，grandfather的父节点还没有被访问，所以it应该指向这里，也就是grandfather->parent节点。

当it右子树不存在时，++it后，it指向的是it所在子树是左子树的最近祖宗节点。

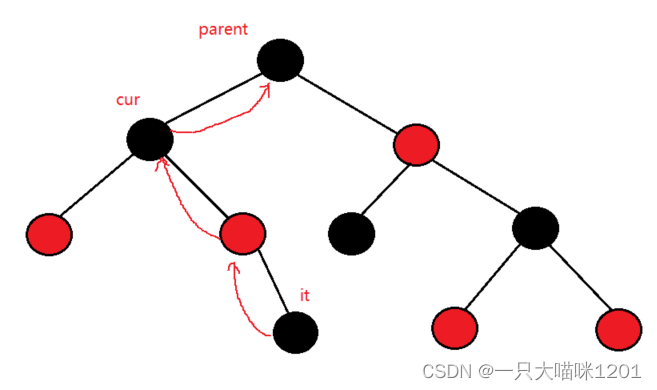
• cur是从it开始向上跟新的，cur更新的同时，它的parent也在更新。
• 当cur是parent是左子树时，让it指向parent即可。

那如果it是最后一个节点呢？

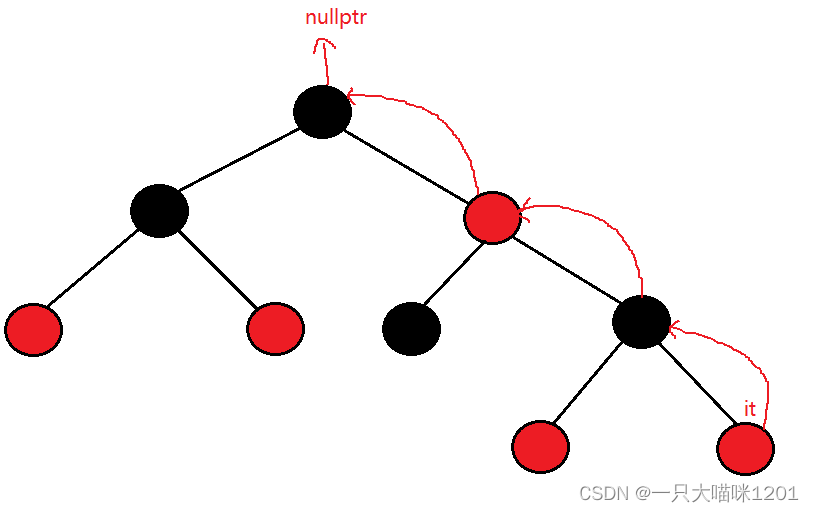
• 当it指向的是红黑树最右边的节点时，再++it后，it应该指向最后一个节点的下一个节点。
• 但是红黑树最后一个节点的下一个节点并没有，所以我们让it指向nullptr。

//右子树不存在
		else
		{
			Node* cur = _node;
			Node* parent = cur->_parent;
			//寻找it是左子树的最近祖宗节点
			while (parent && cur == parent->_right)
			{
				//cur和parent同时更新
				cur = cur->_parent;
				parent = parent->_parent;
			}
			_node = parent;
		}

• 在代码中，无论是找到了++it后的位置，还是it是最后一个节点，都会跳出循环，将it指向跳出循环的parent即可。

再来实现一下后置++：

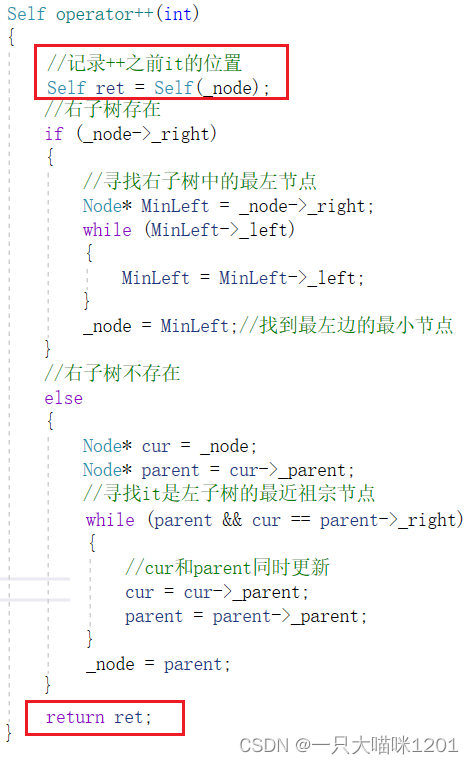
后置++和前置++的唯一不同就是返回的是++之前的位置，其他操作都一样，所以在改变it指向的位置之前，需要提前记录下要返回的it。

• 后置++返回类型不能用引用，因为记录位置的临时变量会销毁。

🍌迭代器–

迭代器减减的逻辑和加加是相反的，所以它的顺序应该是：右子树 根 左子树

左子树存在：

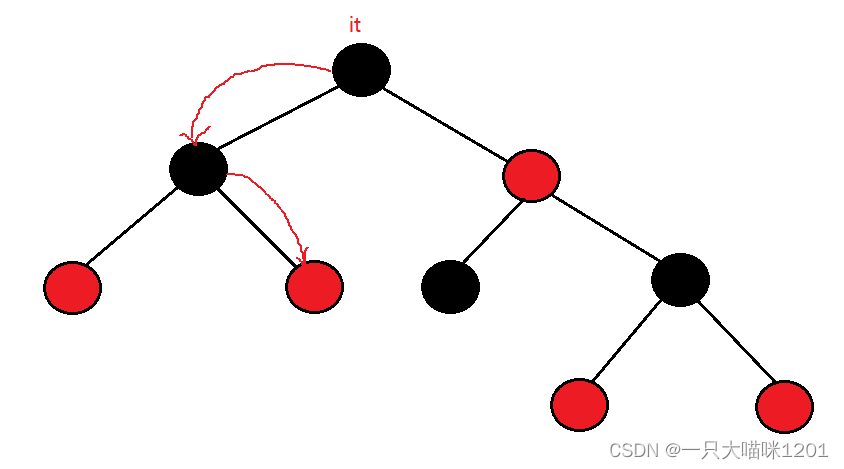
当左子树存在时，it减减后，应该指向的是左子树最右边的节点，如上图所示。

//--it
	Self& operator--()
	{
		//左子树存在
		if (_node->_left)
		{
			//寻找左子树最右边节点
			Node* MaxRight = _node->_left;
			while (MaxRight->_right)
			{
				MaxRight = MaxRight->_right;
			}
			_node = MaxRight;//it指向左子树最右节点
		}
		return *this;
	}

只是逻辑和++相反，本喵就不详细解释了。

左子树不存在：

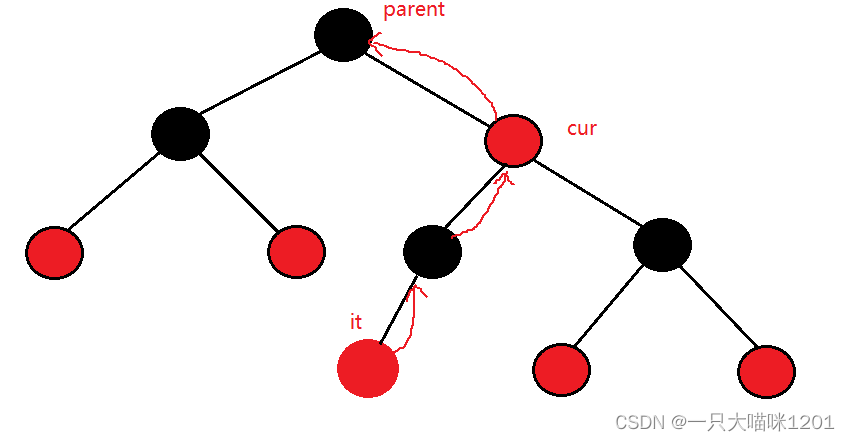
• it是左子树，说明它的根节点就已经被访问过来，所以需要继续向上。
• 当找到it所在子树是右子树的最近祖宗时，将it指向这个祖宗节点。

因为是–，逻辑相反，所以此时减减it后，it指向it所在子树是右子树的最近祖宗节点，同样，当it指向是第一个节点时，减减it会指向空节点。

//左子树不存在
		else
		{
			Node* cur = _node;
			Node* parent = cur->_parent;
			while (parent && cur == parent->_left)
			{
				cur = cur->_parent;
				parent = parent->_parent;
			}
			_node = parent;
		}

再实现一下后置–：

//it--
	Self operator--(int)
	{
		//记录返回节点
		Self ret = Self(_node);
		//左子树存在
		if (_node->_left)
		{
			//寻找左子树最右边节点
			Node* MaxRight = _node->_left;
			while (MaxRight->_right)
			{
				MaxRight = MaxRight->_right;
			}
			_node = MaxRight;//it指向左子树最右节点
		}
		//左子树不存在
		else
		{
			Node* cur = _node;
			Node* parent = cur->_parent;
			while (parent && cur == parent->_left)
			{
				cur = cur->_parent;
				parent = parent->_parent;
			}
			_node = parent;
		}
		return ret;
	}

同样，需要返回的是减减之前的节点，所以需要先记录下来。

🍌迭代器条件判断(==和!=)

    //operator==
	bool operator==(const Self& it) const
	{
		return _node == it._node;
	}
	//operator!=
	bool operator!=(const Self& it) const
	{
		return _node != it._node;
	}

无论是普通对象还是const对象，都可以调用const版本，并且仅仅是进行比较，所以只有const版本的就够用了。

• 比较的内容是两个迭代器指向节点是否相同，而不是节点中的值。

迭代器写好之后，还要在红黑书中封装它，因为我们都是通过红黑树来使用的。

红黑树提供两种版本的迭代器共map和set使用。

• 为了达到迭代器区间是左闭右开[begin，end)，迭代器的起始位置一定是红黑树最左边的节点，也就是第一个，结束位置这里设为空节点。
• 当是一颗空树时，起始位置也是空。

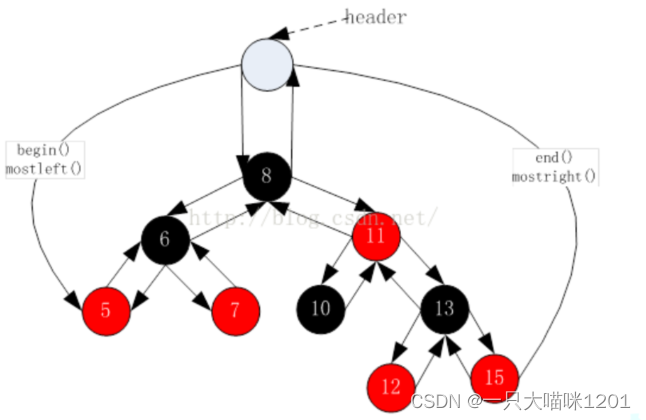
为了实现左闭右开，在STL库中采用上图所示方式，在根节点之前再加一个哨兵位头节点。

• end指向的是哨兵位头节点，红黑树最左边的节点直接和这个头节点相连。
• 红黑树的根也可以通过哨兵位头节点找到，从而进入树中。

有兴趣的小伙伴可以自行去尝试一下这种方式，本喵就不在这里介绍了。

🍉map和set对迭代器的封装

底层的迭代器做好了，下一步就需要把它封装到set和map中：

• 我们知道，红黑树以及AVL树等二叉搜索树是不支持修改节点中的key值的，因为会破坏树的结构。

• set中节点中存放的是key值，所以必然不能被修改，所以它的iterator和const_iterator的底层都是迭代器的const版本，保证set中的数据不能被修改。
• map中节点存放的是键值对，键值对中的key值不可以被修改，但是另一个值可以被修改。键值对的first的类型是const K类型，已经保证了key值不会被修改。所以map提供了普通和const两种迭代器，而且它们的底层也是不一样的，供不同清来使用。

在使用typedef的时候，还需要注意一个点：

typedef typename RBTree<K, K, SetKeyOfT>::iterator iterator;

必须得加关键字typename。

• 当模板类没有进行实例化时，它就是一张图纸，在编译的时候并不参与编译。
• 因为域作用限定符::的存在，编译器在处理这条语句的时候，可能会将::后的iterator当作静态变量处理，参与编译。
• 所以就需要加关键字typename来告诉编译器这是一个模板类型，暂时不参与编译。

像这种已经实例化后的模板类就不用再加typename去表面自己是一个类型了。

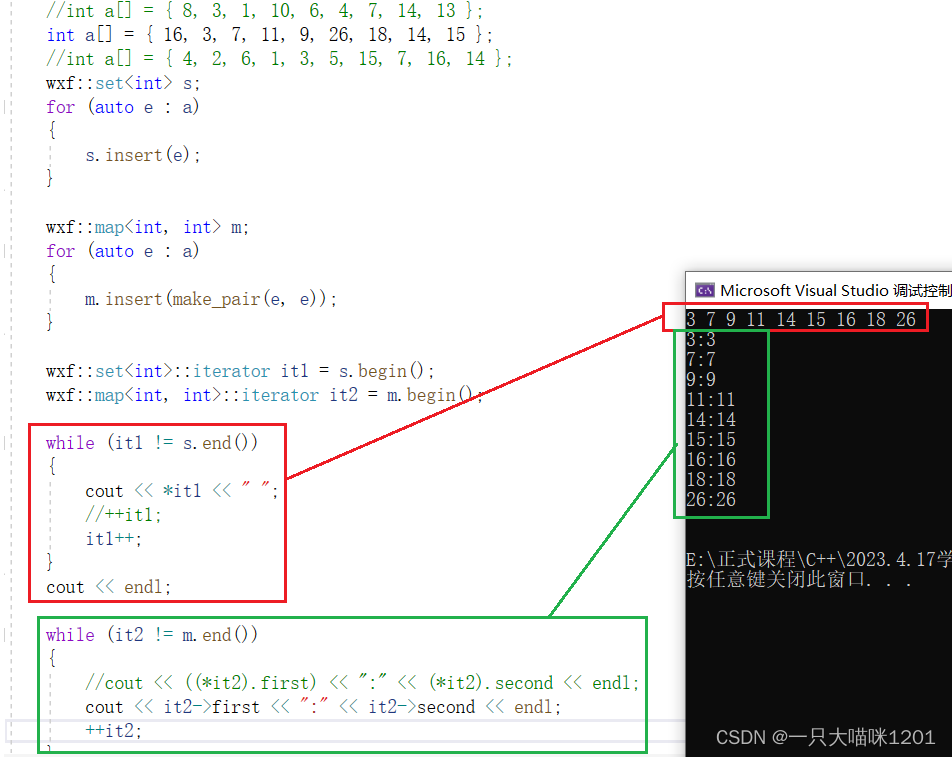
此时我们就可以使用实现的迭代器进行打印了，如上图所示，无论是set和map，都符合我们的预期。

🍉map的operator[]

map有一个特有的[]，可以实现查找，插入，修改三个功能，下面来实现一下。

//operator[]
		T& operator[](const K& key)
		{
			//返回键值对,一个是插入数据所在位置的迭代器
			//一个是bool值,原本存在返回false,不存在则插入并返回true
			pair<iterator, bool> ret = _t.insert(make_pair(key,T()));
			return ret.first->second;
		}

代码看起来很简单,但是存在问题

继续用之前的代码来统计水果个数.

运行时出现的第一个错误就是上图所示的错误.

• 我们在operator中,使用insert返回的是一个键值对<iterator,bool>,而红黑树底层中的insert返回的是一个bool值.

所以需要对红黑树底层中的inset做修改:

• 键值对<iterator, bool>:迭代器是新插入节点的迭代器,bool值表示插入是否成功.
• 如果新节点原本就存在,则返回原本存在节点的迭代器,并且插入失败,返回false.
• 如果新节点不存在,则插入,返回新插入节点在树中的迭代器,并且返回true.

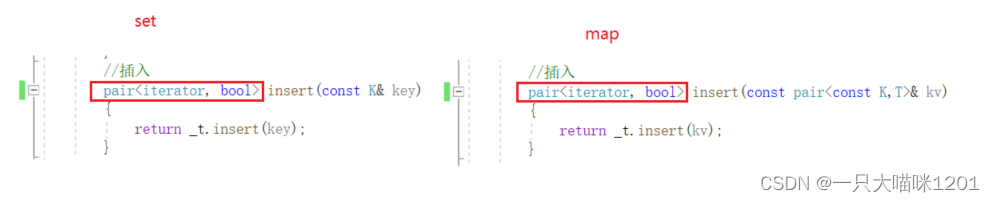
红黑树底层的inset已经被修改了,set和map中的insert也需要被修改,如上图所示.

🍌普通迭代器和const迭代器的转换

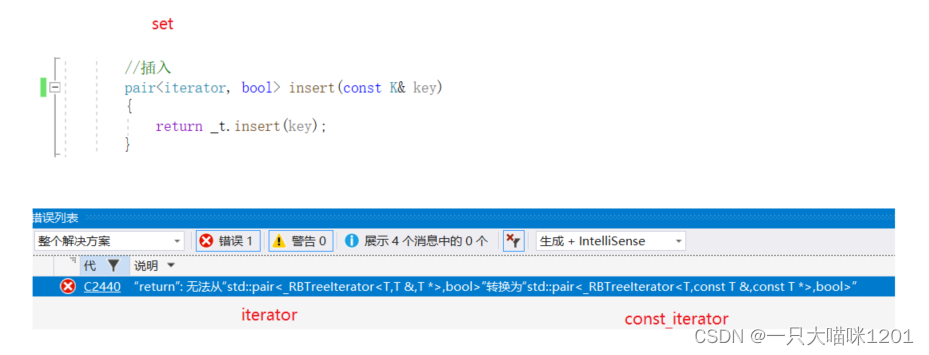
但是此时又出现了一个问题,出现在set里面,如上图所示.

• 红黑树的insert返回的是<iterator, bool>,迭代器是普通迭代器.
• 但是set中的迭代器为了防止key值被修改,iterator和const_iterator都封装的是红黑树的const_iterator.

所以会报无法从普通迭代器转换到const迭代器的错误.

补充知识:

• 类型之间的转换不是任意类型都可以进行转换的,只有强相关的类型才能相互转换.
• 比如不同类型的指针变量,它们就可以相互转换,因为不管怎么转换还是指针.
• 再比如整形家族的不同类型,再怎么转换也还是整数.

普通迭代器和const迭代器是完全不同的两个类型,不能相互转换.

那这个问题怎么处理呢?

在迭代器类模板中作上图所示处理就可以解决了,这一点非常的秒.

• 在set中,红黑树底层的insert返回键值对中的迭代器是普通迭代器.
• 而set中insert返回键值对中的迭代器是const迭代器.

• set中调用insert相当于用红黑树底层的普通迭代器构造set中的const迭代器.

• 迭代器中的拷贝构造函数就是名副其实的构造函数,它的形参是用const修饰的普通迭代器(因为上面typedef了iterator),此时接收来自红黑树底层的普通迭代器是在权限缩小,是被允许的.
• 再用接收到的普通迭代器的值去构造const迭代器,虽然不能直接转换,但是普通迭代器的值const迭代器还是可以使用的.

解释:

• const iteraror的本质是:const _RBTreeIterator<T, T&, T*>
• const_iterator的本质是:_RBTreeIterator<T, const T&, const T*>

const所在位置是完全不一样的,所以它们是完全不同的两个类型.

• 如果是在map中,它的insert返回的迭代器就是普通迭代器,此时迭代器中的拷贝构造函数就是拷贝构造,拷贝从红黑树底层insert返回来的迭代器到map的迭代器.

typedef __RBTreeIterator<T, T&, T*> iterator;

如果没有这个重命名,拷贝构造函数的形参类型就只能用Self,而

typedef __RBTreeIterator<T, Ref, Ptr> iterator;

当set使用insert的时候,Ref和Ptr就已经被推演成了const T& 和 const T*,是一个const迭代器,所以在接收红黑树底层的普通迭代器时也会发生类型无法转换的错误.

• 而使用了重命名后的iterator,无论是set还是map调用它们自己的insert,拷贝构造的形参都是普通迭代器,都可以正常接收红黑底层的普通迭代器.

拷贝构造函数在将普通迭代器转换成const迭代器的时候,充电的是构造函数的角色.

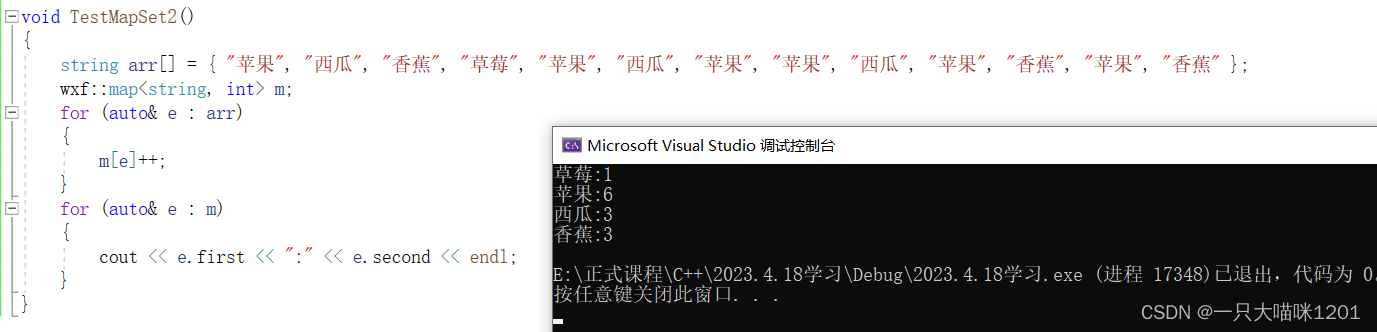
此时便可以成功统计出水果的个数了.

🍉multimap和multiset

multimap和multiset和与map和set的唯一区别就是运行出现重复的节点,这一点在学习使用的时候就详细讲解过.

在源码中,红黑树底层的插入方式有两种,如上图所示.map和set就使用的insert_unique,而multimap和multiset使用的就是insert_equal.

那么允许重复插入时,相等的key应该插入左边还是右边呢?其实都一样:

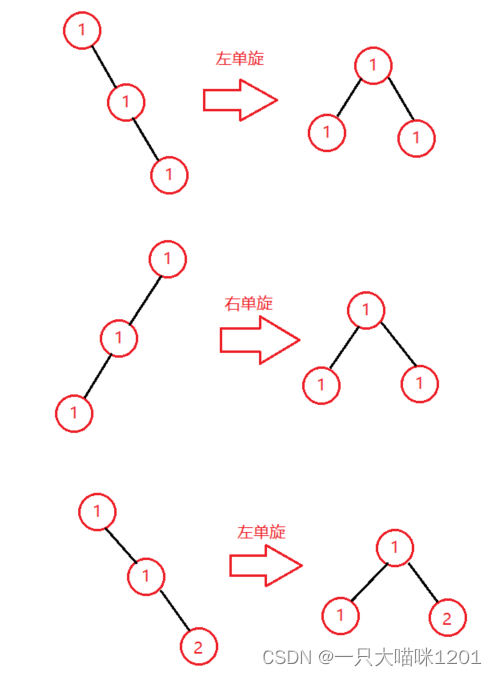
• 无论是插入左边还是右边,都会发生旋转,旋转之后就都一样了.

至于具体的代码实现本喵就不再写了,有兴趣的小伙伴可以自己去尝试.

🍉总结

再说一次,模拟实现容器并不是为了造更好的轮子,而是为了更好的了解这个容器已经一些好的方法.
比如这篇文章中,使用仿函数获取key值进行比较,中序遍历顺序指针的移动,已经使用构造函数将普通迭代器转换成const迭代器的方法,都值得我们学习借鉴.