单链表（邻接表）

双链表

数组模拟栈、队列

单调栈

单调队列（滑动窗口）

KMP

一、KMP算法基本概念与核心思想

二、next数组的含义

三、匹配的思路

四、求next数组

单链表（邻接表）

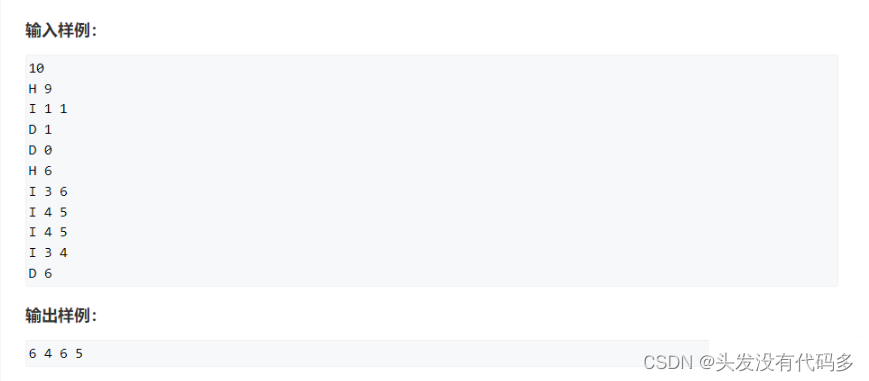
#include <iostream>

using namespace std;

const int N = 100010;

int n;
int h[N], e[N], ne[N], head, idx;

//对链表进行初始化
void init(){
    head = -1;//最开始的时候，链表的头节点要指向-1，
    //为的就是在后面进行不断操作后仍然可以知道链表是在什么时候结束
    /*
    插句题外话，我个人认为head其实就是一个指针，是一个特殊的指针罢了。
    刚开始的时候它负责指向空结点，在链表里有元素的时候，它变成了一个指向第一个元素的指针

    当它在初始化的时候指向-1，来表示链表离没有内容。
    */
    idx = 0;//idx在我看来扮演两个角色，第一个是在一开始的时候，作为链表的下标，让我们好找
    //第二在链表进行各种插入，删除等操作的时候，作为一个临时的辅助性的所要操作的元素的下
    //标来帮助操作。并且是在每一次插入操作的时候，给插入元素一个下标，给他一个窝，感动！
    /*
    再次插句话，虽然我们在进行各种操作的时候，元素所在的下标看上去很乱，但是当我们访问的
    时候，是靠着指针，也就是靠ne[]来访问的，这样下标乱，也就我们要做的事不相关了。
    另外，我们遍历链表的时候也是这样，靠的是ne[]
    */
}
//将x插入到头节点上
void int_to_head(int x){//和链表中间插入的区别就在于它有head头节点
    e[idx] = x;//第一步，先将值放进去
    ne[idx] = head;//head作为一个指针指向空节点，现在ne[idx] = head;做这把交椅的人换了
    //先在只是做到了第一步，将元素x的指针指向了head原本指向的
    head = idx;//head现在表示指向第一个元素了，它不在是空指针了。（不指向空气了）
    idx ++;//指针向下移一位，为下一次插入元素做准备。
}

//将x插入到下标为k的点的后面
void add(int k, int x){
    e[idx] = x;//先将元素插进去
    ne[idx] = ne[k];//让元素x配套的指针，指向它要占位的元素的下一个位置
    ne[k] = idx;//让原来元素的指针指向自己
    idx ++;//将idx向后挪
    /*
    为了将这个过程更好的理解，现在
    将指针转变的这个过程用比喻描述一下，牛顿老师为了省事，想插个队，队里有两个熟人
    张三和李四，所以，他想插到两个人中间，但是三个人平时关系太好了，只要在一起，就
    要让后面的人的手插到前面的人的屁兜里。如果前面的人屁兜里没有基佬的手，将浑身不
    适。所以，必须保证前面的人屁兜里有一只手。（张三在前，李四在后）
    这个时候，牛顿大步向前，将自己的手轻轻的放入张三的屁兜里，（这是第一步）
    然后，将李四放在张三屁兜里的手抽出来放到自己屁兜里。（这是第二步）
    经过这一顿骚操作，三个人都同时感觉到了来自灵魂的战栗，打了个哆嗦。
    */
}

//将下标是k的点后面的点个删掉
void remove(int k){
    ne[k] = ne[ne[k]];//让k的指针指向，k下一个人的下一个人，那中间的那位就被挤掉了。
}
int main(){
    cin >> n;
    init();//初始化
    for (int i = 0; i < n; i ++ ) {
        char s;
        cin >> s;
        if (s == 'H') {
            int x;
            cin >> x;
            int_to_head(x);
        }
        if (s == 'D'){
            int k;
            cin >> k;
            if (k == 0) head = ne[head];//删除头节点
            else remove(k - 1);//注意删除第k个输入后面的数，那函数里放的是下标，k要减去1
        }
        if (s == 'I'){
            int k, x;
            cin >> k >> x;
            add(k - 1, x);//同样的，第k个数，和下标不同，所以要减1
        }
    }

    for (int i = head; i != -1; i = ne[i]) cout << e[i] << ' ' ;
    cout << endl;

    return 0;
}

双链表

int e[N], l[N], r[N], idx;
//e[N]存放数据
//l[N]前一个节点
//r[N]后一个节点
//idx存储当前已经用到了哪个点

如何理解l[N]和r[N]：l[0]代表第一个节点的左端点，1[1]代表第二个节点的左端点，r[0]代表第一个节点的右端点，r[1]代表第二个节点的右端点。

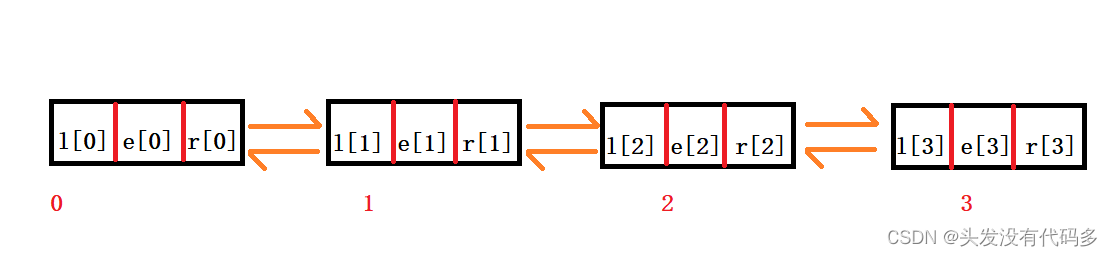
初始化

初始化相当于让最左边俩个连接起来

void Init()
{
	//0表示左端点，1表示右端点
	r[0] = 1;
	l[1] = 0;
	idx = 2;
}

#include<iostream>
using namespace std;
const int N = 100010;
int m;
int e[N], l[N], r[N], idx;
//e[N]存放数据
//l[N]前一个节点
//r[N]后一个节点
//idx存储当前已经用到了哪个点 
//初始化
void Init()
{
	//0表示左端点，1表示右端点
	r[0] = 1;
	l[1] = 0;
	idx = 2;
}
void add_right(int k,int x)//在第k点后面插入x
{
	e[idx] = x;//先建立一个新的节点
	r[idx] = r[k];//让新节点的右边等于k的右边
	l[idx] = k;//让左边指向k
	l[r[k]] = idx;//把k的下一个节点的左边指向idx
	r[k] = idx;//让k的右边指向idx
	idx++;
}
void add_left(int k, int x)//在第k节点前面插入x
{
	add_right(l[k], x);
}
void remove(int k)//删除第k个点
{
	r[l[k]] = r[k];//让k的前面的节点指向k后面节点
	l[r[k]] = l[k];//让k后面节点指向k前面节点
	//不需要对k的左右节点进行处理
}

数组模拟栈、队列

栈

#include<iostream>
using namespace std;
const int N = 100010;
int stk[N], tt;//tt表示栈顶下标

队列

hh是队头，tt队尾

单调栈

如有一组数字3 4 2 7 5，我们返回每个元素左边离它最近且比它小的数，若左边没有比它小的数返回-1

注意这组数据里的4和2，当我们要找比7小的数字时，左边3，4，2都比7小，但我们找的是离7最近的2，此时返回2即可，但3和4此时没用，在找比5小的数字时，3，4也没用，3和4便可以删除。因为3和4大于2。

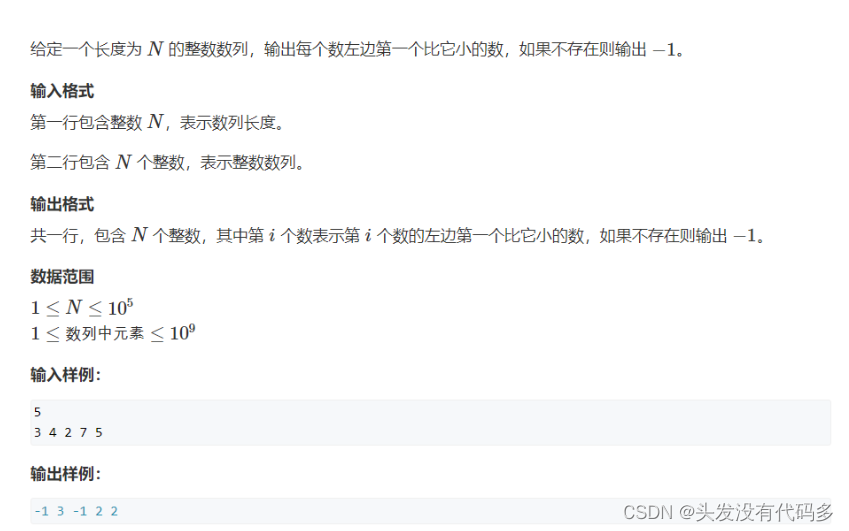
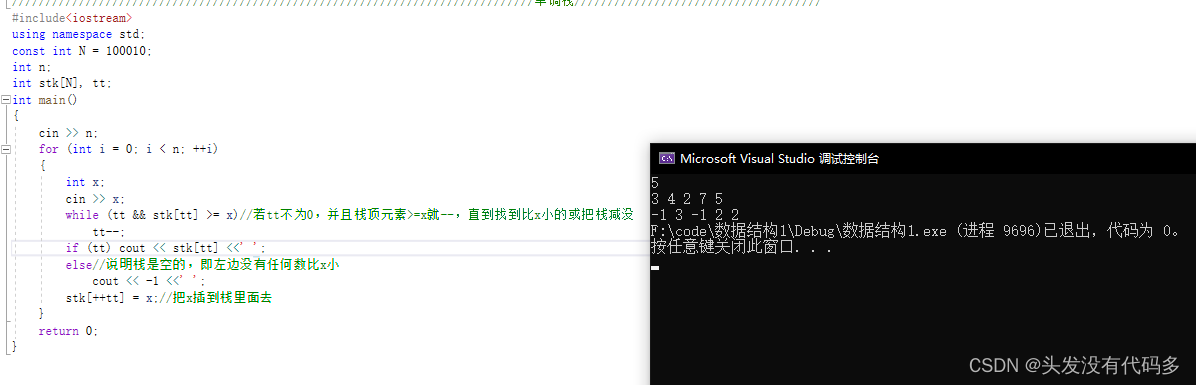
#include<iostream>
using namespace std;
const int N = 100010;
int n;
int stk[N], tt;
int main()
{
	cin >> n;
	for (int i = 0; i < n; ++i)
	{
		int x;
		cin >> x;
		while (tt && stk[tt] >= x)//若tt不为0，并且栈顶元素>=x就--，直到找到比x小的或把栈减没
			tt--;
		if (tt) cout << stk[tt] <<' ';
		else//说明栈是空的，即左边没有任何数比x小
			cout << -1 <<' ';
		stk[++tt] = x;//把x插到栈里面去
	}
	return 0;
}

单调队列（滑动窗口）

把所有长度为3的窗口里面的最大值和最小值输出，这个窗口会移动

以找窗口中的最小值为例：3和-1都比-3大，而且这俩个数字在窗口滑动的时候都会比-3提前被窗口弹出，所以我们可以删掉这俩个元素，即：在找最小的数只要队列里面前面的数比后面的数大，则前面的数一定没有用，这样我们就可以把大的数删掉，当整个数组都这样操作时，队列就会变成一个单调递增的队列

队列的最小值就在左下方，即我们找到队头就可以找到最小的数

q中存的是a中元素对应的下标

#include<iostream>
using namespace std;
const int N = 1000010;
int n,k;
int a[N], q[N];//q单调队列
int main()
{
	scanf("%d%d", &n,&k);//k是窗口长度
              	int hh = 0, tt = -1;
	for (int i = 0; i < n; ++i)
	{
		scanf("%d", &a[i]);
	}
	//找窗口中最小元素
	for (int i = 0; i < n; ++i)
	{
		//判断队头是否已经划出窗口
		if (hh <= tt && i - k + 1 > q[hh])//i-k+1是窗口的起始位置，如果起始位置>对头位置，说明q[hh]已经出窗口了
			hh++;//因为q是单调队列，q[hh]是最小值，要让q[hh]一直位于窗口中
		while (hh <= tt && a[q[tt]] >= a[i])//如果队尾的数大于当前插入的数，则队尾--即删除该数字
			tt--;
		q[++tt] = i;
		if (i >= k - 1)
			printf("%d ", a[q[hh]]);
	
	}
	puts("");
	//找窗口中最大值
	hh = 0, tt = -1;
	for (int i = 0; i < n; ++i)
	{
		//判断队头是否已经划出窗口
		if (hh <= tt && i - k + 1 > q[hh])//i-k+1是窗口的起始位置，如果起始位置>对头位置，说明q[hh]已经出窗口了
			hh++;//因为q是单调队列，q[hh]是最小值，要让q[hh]一直位于窗口中
		while (hh <= tt && a[q[tt]] <= a[i])//如果队尾的数大于当前插入的数，则队尾--即删除该数字
			tt--;
		q[++tt] = i;
		if (i >= k - 1)
			printf("%d ", a[q[hh]]);

	}
	return 0;
}

KMP

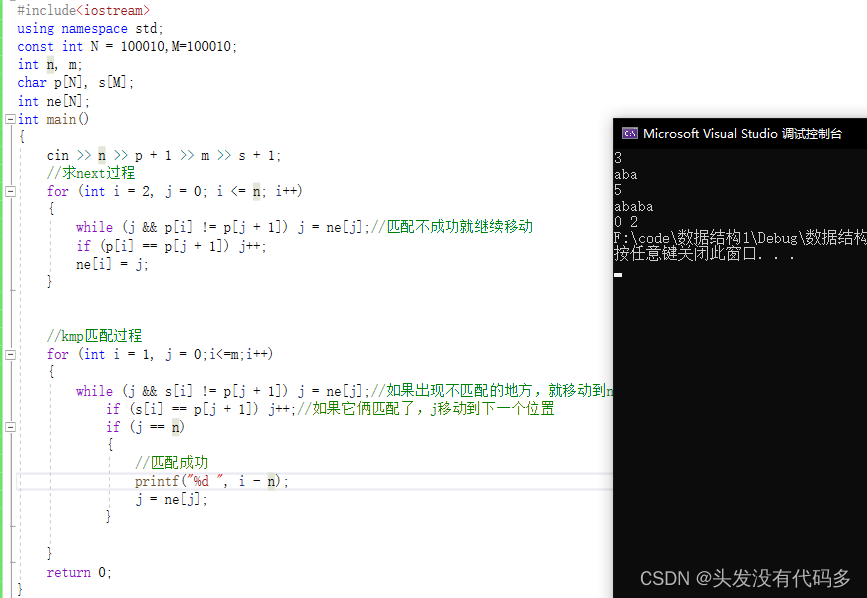
#include<iostream>
using namespace std;
const int N = 10010,M=100010;
char s[M], p[N],ne[N];
int main()
{
	int n,m;
cin >> n >> p+1>>m>>s+1;
//NE数组
//ne数组求法：是通过模板串自己与自己匹配出来的
for (int i = 2, j = 0; i <= n; ++i)
{
	while (j && p[i] != p[i + 1]) j = ne[j];
	if (p[i] == p[j + 1]) j++;
	ne[i] = j;
}
{

}
//匹配部分
for (int i = 1, j = 0; i <=m; ++i)
{
	while (j && s[i] != p[j + 1]) j = ne[j];//如果模板串与父串下一处不匹配，就将模板串移动到下一个匹配的地方
	 if(s[i] == p[j + 1]) j++;//如果下一个地方能匹配上，则把j++
	 if (j == n)//整个模板串都匹配上了,更新一下位置，进行下一次匹配
	 {
		 printf("%d ", i - n);//打印出匹配到的首字符下标，由于i从1开始，所以这里不需要+1
		 j = ne[j];
	 }
}
	return 0;
}

一、KMP算法基本概念与核心思想

基本概念：

① s[ ]是模式串：较长字符串，
② p[ ]是模板串，较短字符串。
③ “非平凡前缀”：指 除了最后一个字符以外，一个字符串的 全部头部组合（前面连续的部分）
④ “非平凡后缀”：指 除了第一个字符以外，一个字符串的 全部尾部组合。（后面均简称为前/后缀）
⑤ “部分匹配值”：前缀和后缀 的 最长共有元素 的长度。
⑥ next[ ]是“部分匹配值表”，即next数组，它存储的是每一个下标对应的“部分匹配值”，是KMP算法的核心。

核心思想：

在每次失配时，不是把p串往后移一位，而是把p串往后移动至下一次可以和前面部分匹配的位置，

这样就可以 跳过大多数的失配步骤。

每次p串移动的步数通过查找next[ ]数组确定的。

二、next数组的含义

含义：next[ j ] 表示p[ 1, j ]串中前缀和后缀相同的最大长度（部分匹配值），

即：p[ 1, next[ j ] ] = p[ j - next[ j ] + 1, j ]（前后缀相同，两者都达到最大）

举个例子，例如：

为了对next数组有更清晰的认知，我们手动模拟一下next数组

假设模板串 p = “abcab”，

则对于next[1]：前缀集合为空，后缀集合为空，next[1] = 0;

next[2]：前缀集合 { “a” }，后缀集合 { “b” }，两集合中无匹配字符串，next[2] = 0;

next[3]：前缀集合 { “a”, “ab” }，后缀集合 { “c”, “bc” }，两集合中无匹配字符串，next[3] = 0;

next[4]：前缀集合 { “a”, “ab”, “abc” }，后缀集合 { “a”, “ca”, “bca” }，两集合中最长匹配字符串为 “a”，next[4] = 1;

next[5]：前缀集合 { “a”, “ab”, “abc”, “abca” }，后缀集合 { “b”, “ab”, “cab”, “bcab” }，两集合中最长匹配字符串为 “ab”，next[5] = 2;

（注意以上说的前后缀都指的是“非平凡”）

得到以下表格：

三、匹配的思路

KMP算法主要分两步：求next数组、匹配字符串。

对于匹配字符串，其思路是这样子的：

模式s串和模板p串都人为规定为从1开始。

i 从1开始，j 从0开始，每次将s[ i ] 和p[ j + 1 ]比较。

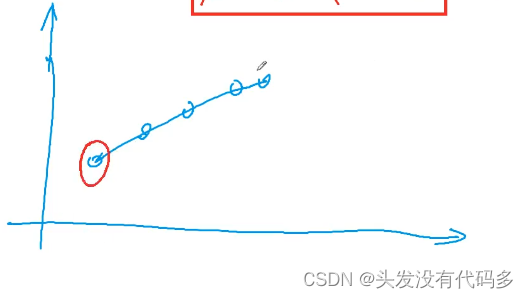
下方的图中，红色的字符串代表模式s串，蓝色和紫色的串代表匹配过程中后移的模板p串，

当匹配过程到上图所示时，

s[ a , b ] = p[ 1, j ] && s[ i ] != p[ j + 1 ] 此时要移动p串（不只移动1格，而是直接移动到下次能匹配的位置）

其中上图中的 ①串为[ 1, next[ j ] ]，③串为[ j - next[ j ] + 1 , j ]。由匹配可知 ①串等于 ③串，③串等于 ②串。所以 直接移动p串，使 ① 到 ③ 的位置 即可。这个操作可由 j = next[ j ] 直接完成。 如此往复下去，当 j == m时匹配成功（此时就能够完全匹配上了：p串最后一个元素p[m]与s相配了）。

匹配过程的代码片段：

for(int i=1, j=0; i<=n; ++i)
{
        while(j && s[i]!=p[j+1]) j = ne[j];
        //如果j有对应p串的元素， 且s[i] != p[j+1], 则失配， 移动p串
    	//用while是由于移动后可能仍然失配，所以要继续移动直到匹配或整个p串移到后面（j = 0)

        if(s[i]==p[j+1]) ++j;
        //当前元素匹配，j移向p串下一位
        if(j==m)//满足匹配条件
        {
                //匹配成功，进行相关操作
                        
                j = ne[j];//继续匹配下一个子串
        }
}

四、求next数组

next数组的求法是通过 模板串 自己与自己 进行匹配操作得出来的（代码和匹配操作几乎一样）。

始终记住一点： next[ ]是“部分匹配值表”，即next数组，它存储的是字符串中（一般是模板串p中）每一个下标对应的“部分匹配值”，是KMP算法的核心。

代码和匹配操作的代码几乎一样，关键在于：每次移动 i 前，将 i 前面已经匹配的长度记录到next数组中。

代码片段如下：

void get_next()//核心是求模式串p的next数组(记住next数组是相对于模式串而言的)
{
        for(int i=2, j=0; i<=m; ++i)//i从2开始,因为ne[1]=0,无需计算
        {
                while(j && p[i]!=p[j+1]) j = ne[j];
                if(p[i]==p[j+1]) ++j;//此时匹配到了前后缀相等
                ne[i] = j;//赶紧记录下来
        }
}

二、求next[ ]数组的代码
next[ ]数组的求法，是通过模式串T自己与自己进行匹配得出来的（代码和下文“匹配字符串”的操作几乎一样）。

for(int i=1, j=0; i<=n; ++i)
{
        while(j && s[i]!=p[j+1]) j = ne[j];
        //如果j有对应p串的元素， 且s[i] != p[j+1], 则失配， 移动p串
    	//用while是由于移动后可能仍然失配，所以要继续移动直到匹配或整个p串移到后面（j = 0)

        if(s[i]==p[j+1]) ++j;
        //当前元素匹配，j移向p串下一位
        if(j==m)//满足匹配条件
        {
                //匹配成功，进行相关操作
                        
                j = ne[j];//继续匹配下一个子串
        }
}

下图是T[a,b]=T[1,j]时，模式串T的状态。

若执行语句 if(t[i]==t[j+1]) j++; 后，将产生下图的状态，再结合next[ ]数组的定义，分析可得 next[i]=j;若注意到下图中，绿色虚线框内的元素是相同的，再结合next[ ]数组的定义就更好理解所得结论了。

三、匹配字符串的代码
next[ ]数组在某字符处对应的值的大小，即图中黄色花括号表示的大小。

for(int i=1, j=0; i<=n; i++) { //匹配操作。i从1开始，j从0开始
	while(j && s[i]!=t[j+1]) j=ne[j];
	if(s[i]==t[j+1]) j++;
	if(j==m) {
		cout<<i-m<<" ";
		j=ne[j]; //再次继续匹配
	}
}