K-近邻算法(KNN)

K Nearest Neighbor算法又叫KNN算法，它的原理是如果一个样本在特征空间中的k个最相似（即特征空间中最邻近）的样本中的大多数属于某一个类别，则该样本也属于这个类别。

两个样本间距离可通过欧式距离计算，如a(a1,a2,a3)，b(b1,b2,b3)，则：

$d=\sqrt{(a1-b1)^{2}+(a2-b2)^{2}+(a3-b3)^{2}}$

k值取的太小容易受到异常点的影响，而取的过大容易受到样本不均衡的影响。

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import StandardScaler


def knn_demo():
    # 1）读取数据
    iris = load_iris()

    # 2）划分数据集
    x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=6)  # 前两个参数传的是特征值和目标值

    # 3）特征工程：标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)  # fit_transform其实是fit计算均值、标准差和transform按照计算的均值、标准差将数据转换两个步骤，它们都是转换器
    x_test = transfer.transform(x_test)  # 这里测试集需要用训练集的均值和标准差来进行转换，所以transform就好

    # 4）KNN算法预估器
    estimator = KNeighborsClassifier(n_neighbors=3)  # estimator是预估器，n_neighbors=3即k值为3的意思，不填默认为5
    estimator.fit(x_train, y_train) # 这里的fit做的工作是训练模型（也是计算的一种）

    # 5）模型评估
    # 方法一：直接比对真实值和预测值
    y_predict = estimator.predict(x_test)
    print("y_predict：\n", y_predict)
    print("直接比对真实值和预测值：\n", y_test == y_predict)  # 每个数据都比对，相等的返回True
    # 方法二：计算准确率
    score = estimator.score(x_test, y_test)  # 相当于在方法一比对的基础上算出了预测的准确率
    print("准确率为：\n", score)

    return None


if __name__ == "__main__":
    knn_demo()

模型的选择与调优

交叉验证
超参数搜索

交叉验证(cross validation)

目的是为了让训练得到的模型结果更加准确。做法：将拿到的训练数据，分为训练集和验证集。以下图为例：将数据分成4份，其中一份作为验证集，然后经过4次(组)的测试，每次都更换不同的验证集，即得到4组模型的结果，取平均值作为最终结果，称为4折交叉验证。

训练集：训练集+验证集
测试集：测试集

超参数搜索-网格搜索(Gird Search)

通常情况下，有很多参数是需要手动指定的（如k-近邻算法中的k值），这种叫超参数。但是手动调参繁杂，所以需要对模型预设几种超参数组合。每种超参数都采用交叉验证来进行评估，最后选出最优参数组合建立模型。

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import StandardScaler


def knn_gscv_demo():
    # 1）读取数据
    iris = load_iris()

    # 2）划分数据集
    x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=6)

    # 3）特征工程：标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)

    # 4）KNN算法预估器
    estimator = KNeighborsClassifier()
    # 加入网络搜索与交叉验证
    param_dict = {"n_neighbors": [1, 2, 3, 4, 5, 6, 7, 8]}  # 参数列表：相当于后面for循环一遍这些参数看看哪个好
    estimator = GridSearchCV(estimator, param_grid=param_dict, cv=10)  # 数据量不大时cv可以大一些，即交叉验证分割的多一些，否则数据量大时cv又大会太耗时间

    estimator.fit(x_train, y_train)

    # 5）模型评估
    # 方法一：直接比对真实值和预测值
    y_predict = estimator.predict(x_test)
    print("y_predict：\n", y_predict)
    print("直接比对真实值和预测值：\n", y_test == y_predict)
    # 方法二：计算准确率
    score = estimator.score(x_test, y_test)
    print("准确率为：\n", score)  # 这里的准确率是训练集+测试集这个结构中测试集的预测准确率

    print("最佳参数：\n", estimator.best_params_)
    print("最佳结果：\n", estimator.best_score_)  # 这里的最佳结构是测试集=测试集+验证集中验证集的结果
    print("最佳估计器：\n", estimator.best_estimator_)
    print("交叉验证结果：\n", estimator.cv_results_)

    return None


if __name__ == "__main__":
    knn_gscv_demo()

朴素贝叶斯算法

朴素是因为加了个假设：特征与特征之间是相互独立的。故朴素贝叶斯算法=朴素+贝叶斯公式。

贝叶斯公式：

$p(c|w)=\frac{p(w|c)p(c)}{p(w)}$

注：w为给定文档的特征值，c为文档类别。

一般还需要引入拉普拉斯平滑系数进行计算，目的是为了防止计算出的分类概率为0（数据少时易出现）。

$P(F1|C)=\frac{Ni+\alpha }{N+\alpha m}$

$\alpha$ 为指定系数一般为1，m为训练文档中统计出的特征词个数。

from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import MultinomialNB


def nb_demo():
    """
    用朴素贝叶斯算法对新闻进行分类
    :return:
    """
    # 1）读取数据
    news = fetch_20newsgroups(subset="all")  # 数据集较大用fetch，subset默认是获取训练集，都要就all

    # 2）划分数据集
    x_train, x_test, y_train, y_test = train_test_split(news.data, news.target)

    # 3）特征工程：文本特征抽取-tfidf
    transfer = TfidfVectorizer()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)

    # 4）朴素贝叶斯算法预估器流程
    estimator = MultinomialNB()
    estimator.fit(x_train, y_train)

    # 5）模型评估
    # 方法一：直接比对真实值和预测值
    y_predict = estimator.predict(x_test)
    print("y_predict：\n", y_predict)
    print("直接比对真实值和预测值：\n", y_test == y_predict)
    # 方法二：计算准确率
    score = estimator.score(x_test, y_test)
    print("准确率为：\n", score)

    return None


if __name__ == "__main__":
    nb_demo()

缺点：由于加了样本属性独立性的假设，所以如果特征属性有关联时效果不好。

决策树

类似于if-else嵌套构建起的一颗树。

信息熵

简单来说信息是消除随机不定性的东西，比如当我不知道小明的年龄时，小明说他今年18岁，那么小明的话就是一条信息，这时小华接着说小明明年19岁，小华的话就不是信息了。而要衡量消除的不确定性有多少，就引入了信息熵。

$H(x)=-\sum_{i=1}^{n}P(x_{i})log_{b}P(x_{i})$

H的专业术语称之为信息熵，单位为比特，其中底数b一般为2。

决策树的划分条件之一：信息增益

特征A对训练数据集D的信息增益g(D,A)，定义为集合D的信息熵H(D)于特征A给定条件下D的信息条件熵H(D|A)之差：

$g(D,A)=H(D)-H(D|A)$

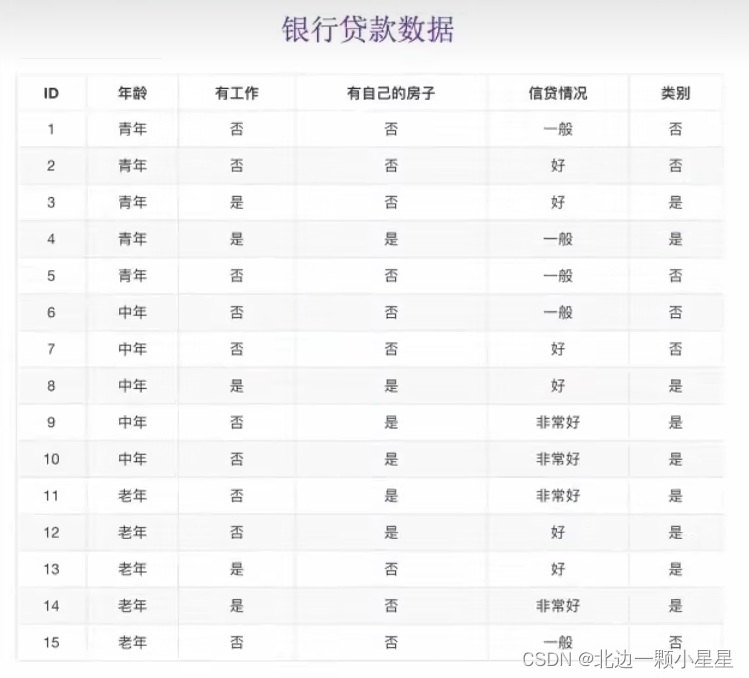
比如从下面这个例子来理解公式，应该选取什么特征开始构建一棵树，从而决策是否贷款。

from matplotlib import pyplot as plt
from sklearn import tree
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier, plot_tree


def decision_demo():
    """
    用决策树进行分类
    :return:
    """
    # 1）读取数据
    iris = load_iris()
    feature_names = iris.feature_names

    # 2）划分数据集
    x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=22)

    # 3）决策树预估器
    estimator = DecisionTreeClassifier(criterion="entropy")  # 表示用信息增益的熵分类
    estimator.fit(x_train, y_train)

    # 4）模型评估
    # 方法一：直接比对真实值和预测值
    y_predict = estimator.predict(x_test)
    print("y_predict：\n", y_predict)
    print("直接比对真实值和预测值：\n", y_test == y_predict)
    # 方法二：计算准确率
    score = estimator.score(x_test, y_test)
    print("准确率为：\n", score)

    # 5）决策树的可视化
    # 指定图幅大小
    plt.figure(figsize=(18, 12))
    # 绘制图像
    _ = tree.plot_tree(estimator, filled=True, feature_names=feature_names)  # 由于返回值不重要，因此直接用下划线接收
    plt.show()
    # 保存图像
    # plt.savefig('./tree.jpg')  # 如果要保存图片记得将plt.show()注释先

    return None


if __name__ == "__main__":
    decision_demo()

集成学习方法之随机森林

集成学习通过建立几个模型组合来解决单一预测问题。它的工作原理是生成多个分类器/模型，各自独立的学习和作出预测，这些预测最后结合成组合预测，因此优于任何一个单分类的作出预测。在机器学习中，随机森林是一个包含多个决策树的分类器，并且其输出的类别是由个别树输出的类别的众数决定。

from sklearn.datasets import load_iris
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split, GridSearchCV


def rf_demo():
    """
    用随机森林进行分类
    :return:
    """
    # 1）读取数据
    iris = load_iris()

    # 2）划分数据集
    x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=22)

    # 3）随机森林预估器
    estimator = RandomForestClassifier()
    # 加入网格搜索与交叉验证
    # n_estimators是森林里树的个数，max_depth是树的最大深度
    param_dict = {"n_estimators": [120, 200, 300, 500, 800, 1200], "max_depth": [5, 8, 15, 25, 30]}
    estimator = GridSearchCV(estimator, param_grid=param_dict, cv=3)
    estimator.fit(x_train, y_train)

    # 4）模型评估
    # 方法一：直接比对真实值和预测值
    y_predict = estimator.predict(x_test)
    print("y_predict：\n", y_predict)
    print("直接比对真实值和预测值：\n", y_test == y_predict)
    # 方法二：计算准确率
    score = estimator.score(x_test, y_test)
    print("准确率为：\n", score)

    # 最佳参数：best_params_
    print("最佳参数：\n", estimator.best_params_)
    # 最佳结果：best_score_
    print("最佳结果：\n", estimator.best_score_)
    # 最佳估计器：best_estimator_
    print("最佳估计器:\n", estimator.best_estimator_)
    # 交叉验证结果：cv_results_
    print("交叉验证结果:\n", estimator.cv_results_)

    return None


if __name__ == "__main__":
    rf_demo()