博主简介

博主是一名大二学生，主攻人工智能研究。感谢让我们在CSDN相遇，博主致力于在这里分享关于人工智能，c++，Python，爬虫等方面知识的分享。如果有需要的小伙伴可以关注博主，博主会继续更新的，如果有错误之处，大家可以指正。

专栏简介：本专栏主要研究计算机视觉，涉及算法，案例实践，网络模型等知识。包括一些常用的数据处理算法，也会介绍很多的Python第三方库。如果需要，点击这里订阅专栏。

给大家分享一个我很喜欢的一句话：“每天多努力一点，不为别的，只为日后，能够多一些选择，选择舒心的日子，选择自己喜欢的人！”

卷积神经网络基本结构

卷积层

池化层

全连层

Softmax激活函数

交叉熵损失

AlexNet详解

卷积神经网络的优点

2012年，AlexNet横空出世，卷积神经网络从此火遍大江南北。此后无数人开始研究，卷积神经网络终于在图像识别领域超过人类，那么卷积神经网络有什么神奇？下面我们来了解了解。

卷积神经网络基本结构

与最早的神经网络不同，除了全连接之外，卷积神经网络加入了卷积层和池化层。卷积层和我们在传统计算机视觉中的卷积极为相似，而池化层主要用于减少参数的数量，防止过拟合。

卷积层

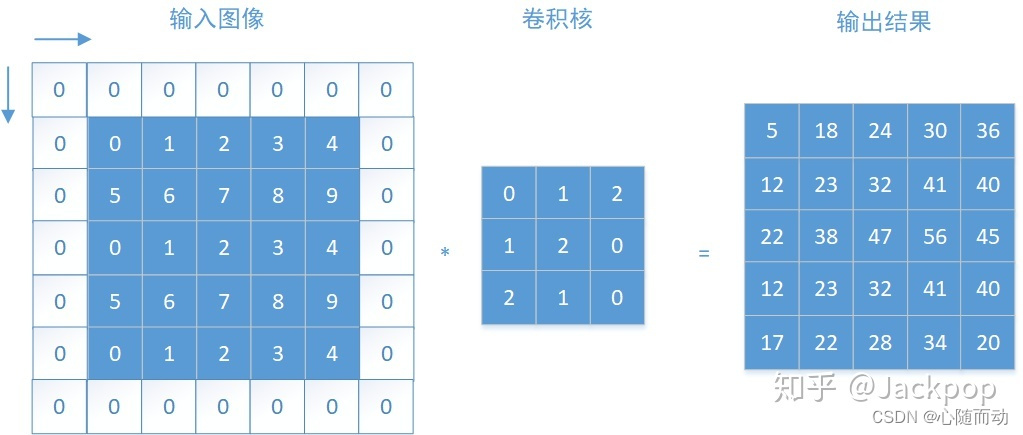
卷积层，英文名convolution layer，卷积层是卷积神经网络的核心，每个卷积层由多个卷积核组成。当输入图像经过卷积核时，每个通道的图像会与每个卷积核进行卷积操作。

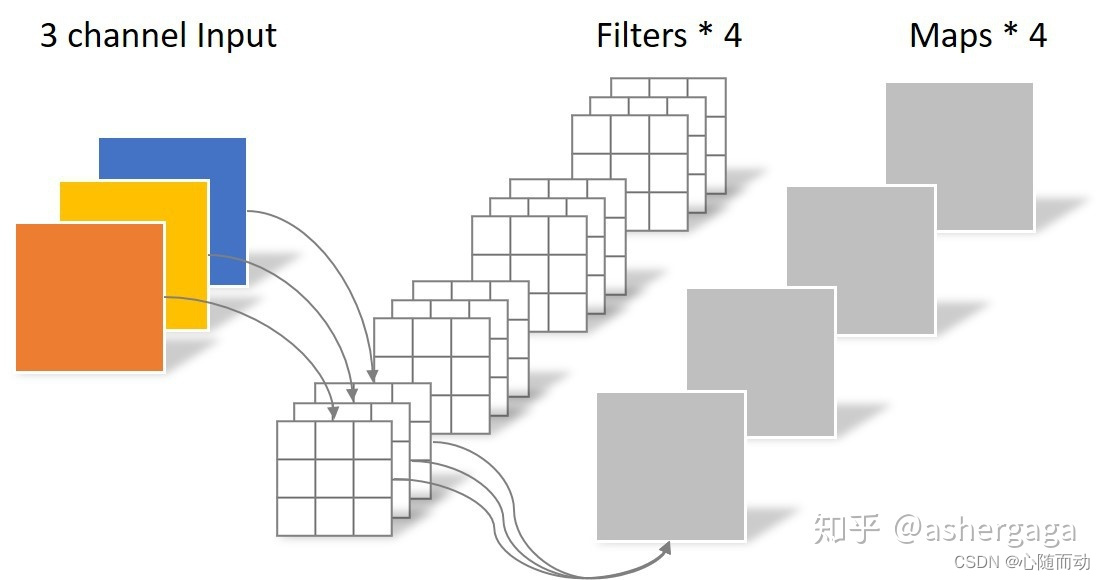$\begin{pmatrix} a_{1} &a_{2} &a_{3} \\ a_{4} &a_{5} &a_{6} \\ a_{7}&a_{8} &a_{9} \end{pmatrix}*\begin{pmatrix} b_{1}&b_{2} &b_{3} \\ b_{4}&b_{5} &b_{6} \\ b_{7}&b_{8} &b_{9} \end{pmatrix}=\sum a_{i}b_{i}$

$\begin{bmatrix} 1 & 1 & 1 & 1 &1 \\ 2& 2 & 2 & 2 & 2\\ 3 &3 & 3 & 3 &3 \\ 4 &4 & 4 &4 &4 \\ 5 & 5 &5 & 5 &5 \end{bmatrix}*\begin{pmatrix} 1 &1 &1 \\ 1 &1 &1 \\ 1 &1 &1 \end{pmatrix}=\begin{pmatrix} 18 &18 &18 \\ 27& 27 &27 \\ 36& 36 &36 \end{pmatrix}$

输入图片经过卷积层后变为多通道输出。具体操作如下图：

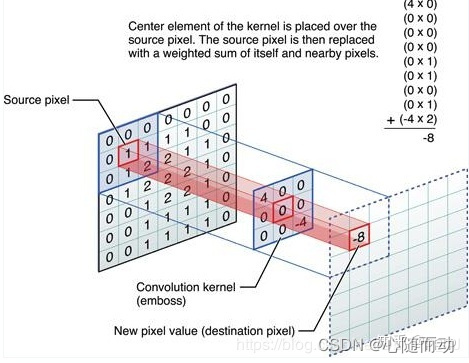
下面这张图片可能更加清楚：

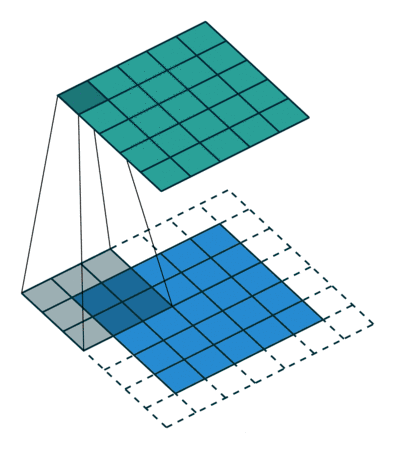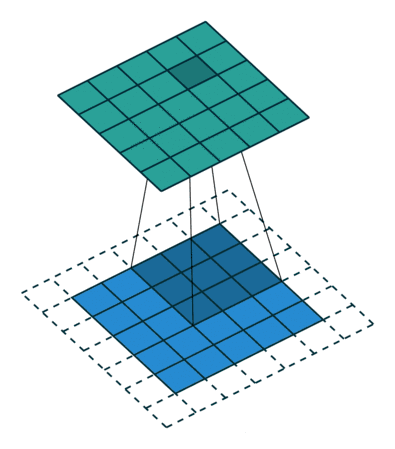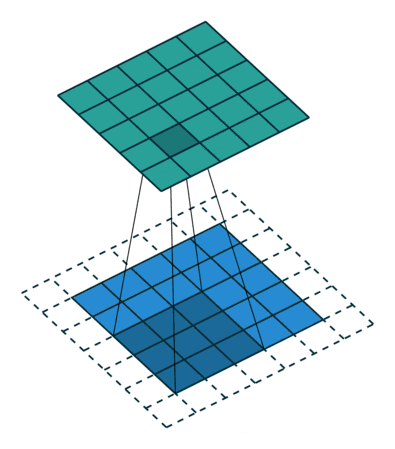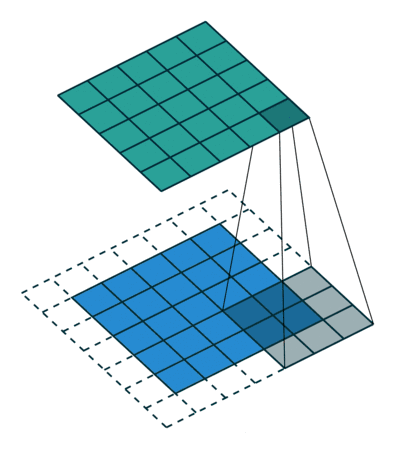
一般的情况下，如果输入图像的大小为n1*n2,卷积核的大小为m1*m2,(mi<ni).卷积后，卷积核水平滑动距离为s1，竖直滑动距离为s2，则输出图像大小为k1*k2,

$k_{1}=\frac{n_{1}-m_{1}+1}{s1},k_{2}=\frac{n_{2}-m_{2}+1}{s2}$

这里需要注意的是，当卷积核滑动到图片末尾时，当剩余的像素数量不够一次滑动时，会自动忽略剩余的像素。由于这种卷积方式会忽略边缘的像素（边缘的像素只计算一次，而中心的像素被计算多次），所以有了第二种卷积方式，我们称之为填充（padding），很简单，在边缘之外加入像素值为0的行和列。这样，新的像素值为0的行和列变为新的边缘，而旧的边缘则变为内部的像素，从而可以被计算多次。

padding操作卷积后特征大小为：

$k_{1}=Floor(\frac{n_{1}-m_{1}+2*p_{1}}{s_{1}})+1$

$k_{2}=Floor(\frac{n_{2}-m_{2}+2*p_{2}}{s_{2}})+1$

Floor表示向下取整，p1和p2表示padding补充单列0的行和列。

最后，如果卷积核的数量为n，则输出特征图片共有n个通道。如果输入图像通道数为c，则每个卷积核的通道数为c，卷积层的参数个数为：每个卷积核大小×c×n。

池化层

池化层，英文名（pooling layer），将图片分成一个一个池子，每个池子输出一个值。池化层可以扩大或者缩小图像的大小，而且还能保证图片的像素不发生变化。常用的池化层：

$\begin{bmatrix} 1 &2 \\ 3& 4 \end{bmatrix}\rightarrow2.5$ 经过平均池化;

$\begin{bmatrix} 1 &2 \\ 3& 4 \end{bmatrix}\rightarrow 4$ 经过最大池化

假设池化层的参数为m1*m2,输入图像大小为n1*n2,则输出图像大小为 $\begin{bmatrix} n1\\m1 \end{bmatrix}*\begin{bmatrix} n2\\m2 \end{bmatrix}$ ,输入图像和输出图像的通道相同。池化层也有stride和padding操作，同卷积层的操作规则一样。

全连层

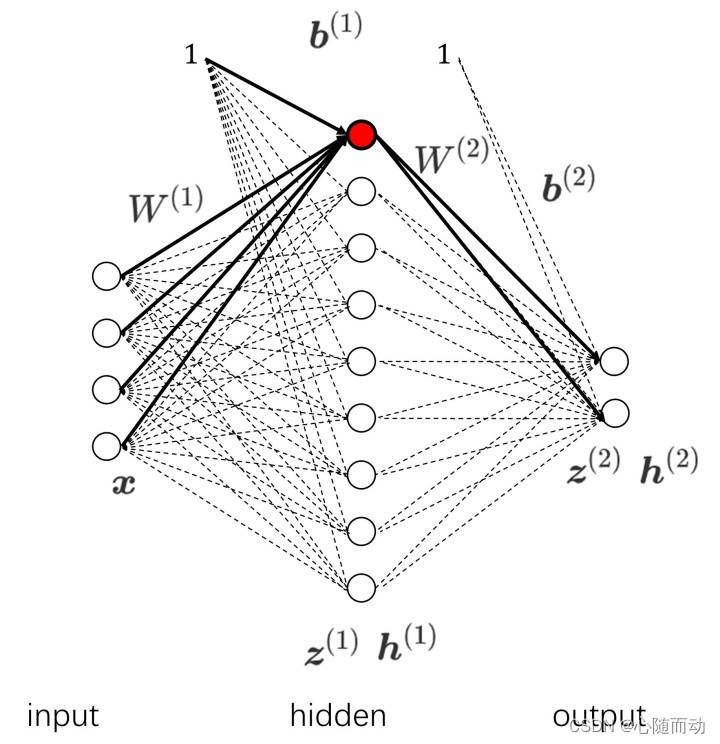
全连接层与最早的人工神经网络的线性层一样。但是，图象是二维的，我们常用的全连接层是一维的，所以我们想要将其“压扁”为一维：

$\begin{bmatrix} 1 &1 \\ 1& 1 \end{bmatrix}=\begin{bmatrix} 1 &1 &1 &1 \end{bmatrix}$

全连接层的作用相当于对输入向量左乘矩阵，假设输入向量为x，全连接层对应矩阵为W，输出为'x'：

$(x^{'})^{T}=wx^{T}$

Softmax激活函数

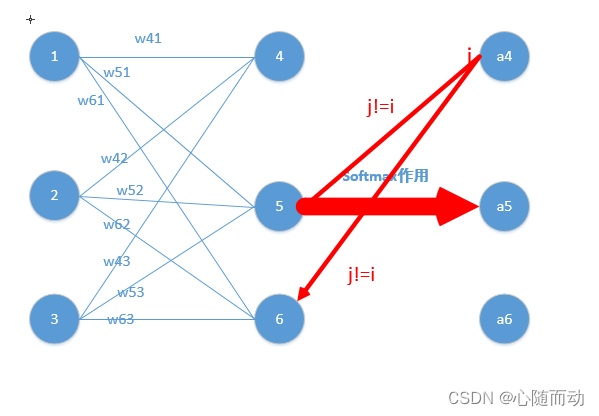
在卷积神经网络的最后一层，激活函数与之前每一层的的激活函数不同。由于最后一层要作为分类的结果，我们希望输出结果（一维向量的值）为各分类的概率，那么概率最大的那个分类就是我们得到的预测结果。例如输出为[0.2,0.3,0.4,0.1,0.1],那么我们就以第三类为预测结果。

如何使输出的结果为概率值？这里就需要用到Softmax激活函数。为了使得输出结果为概率值，首先我们需要将每一个值限制在0~1.其次是需要一个向量所有值的和为1，最后函数应该为单调递增的函数。所以我们选用归一化的指数函数作为激活函数式：

$\begin{bmatrix} x_{1} & x_{2} &... &x_{4} \end{bmatrix}softmax\rightarrow \begin{bmatrix} \frac{e^{x_{1}}}{\sum e^{x_{i}}} &\frac{e^{x_{2}}}{\sum e^{x_{i}}} & ...& \frac{e^{x_{n}}}{\sum e^{x_{i}}} \end{bmatrix}$

交叉熵损失

最后，我们使用交叉熵损失作为损失函数，主要是因为这种损失使得我们一开始的训练速度很快。交叉熵的概念从熵的概念引申而来，所以计算公式非常相似。假设我们的输出直播为X=[x1,x2,x3,x4,x5,,,,xn],标签为Y=[y1,y2,y3,,,yn]，则损失函数的值为：

$\sum -y_{i}log(x_{i}))$

AlexNet详解

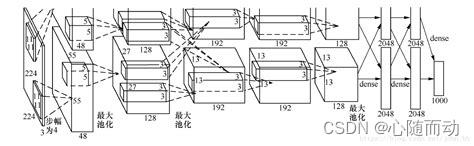
我们现在来解析一下AlexNet的结构。首先输入图像大小为227x227x3.

第一层为卷积层，卷积核大小为11x11，共96个卷积核，由两个GPU分别训练，滑动步长为4，激活函数为ReLU，所以输出图像的特征大小为55x55x96.

第二层为池化层，核大小为3x3，每次滑动步长为2，所以图片大小为27x27x96（（55-3）/2+1）

第三层为卷积层，卷积核大小为5x5，共256个卷积核，每次滑动步长为1，对图像做两个像素的填充，激活函数为ReLU，所以输出特征图为27x27x256(其中27+2x2-5+1).

第四层为池化层，核大小为3x3，每次滑动步长为2，所以输出图像大小为13x13x256（（27-3）/2+1）。

第五层为卷积层，卷积核大小为3x3，共384个卷积核，每次滑动步长为1，对图像做一个像素的填充，激活函数为ReLU，所以输出特征图为13x13x384(其中13+1x2-3+1=13).

第六层为卷积层，卷积核大小为3x3，共384个卷积核，每次滑动步长为1，对图像做一个像素的填充，激活函数为ReLU，所以输出特征图为13x13x384(其中13+1x2-3+1=13).

第七层为卷积层，卷积核大小为3x3，共256个卷积核，每次滑动步长为1，对图像做一个像素的填充，激活函数为ReLU，所以输出特征图为13x13x256(其中13+1x2-3+1=13).

第四层为池化层，核大小为3x3，每次滑动步长为2，所以输出图像大小为6x6x256（（13-3）/2+1=6）.

之后将特征图重构为至一维：9216x1.

第九层为全连接层，输出为4096x1,激活函数为ReLU。

第十层为Dropout层，神经元激活的概率为0.5.

第十一层为全连接层，输出为4096x1,激活函数为ReLU。

第十二层为Droupout层，神经元激活的概率为0.5.

第十三层，也是最后一层为全连接层，输出为1000x1，激活函数为Softmax。

最后使用交叉熵损失进行多分类训练。

前面说了，图像最好是227x227大小，这是因为经过所有的处理，他们的除都是整数，比较方便处理，所以最好设定为227x227x3大小。

总共的参数个数就为：62367776（59.5M）。

卷积神经网络的优点

卷积神经网络现在比全连接神经网络更获得原因：

第一，减少了网络参数，例如大小为28x28x3的图像，经过3x3x32的卷积层，输出为28x28x32的特征图，卷积层的参数为3x3x3x32=864，而如果使用一个全连接层，参数数量为28x28x3x28x28x32=59006976，大了几个数量级，由于减少了网络参数，大大减少了过拟合的可能，从而增加了网络的准确率。

第二，保留了局部特征，由于卷积层比起全连接层更注重局部特征，更能对较小的物体进行识别，而图像中的物体往往占整个图像的比例不高，所以物体的局部特征更重要。

第三，卷积层具有平移不变性。就是说，相同的两个图片，无论卷积层怎么移动，他们的输出值是一样的，不会变。

好了，本节内容就到此结束了，下一节我们学习Tensorflow深度学习，拜拜了你嘞！

点赞加关注不迷路