计算机图形学-算法总结

一、直线转换

1、DDA算法

$$\begin{gathered} \Delta y=y_n-y_0 \\ \Delta x=x_n-x_0 \\ \epsilon =\frac{1}{max(|\Delta x|,|\Delta y|)} \end{gathered}$$
把区间分成$Max(|\Delta x|,|\Delta y|)$个，需要循环这么多次。

每次算出的x，y都需要+0.5，进行向下取整运算。（因为在显示屏上，都是整数，没有小数）。

int x0,y0,xn,yn;
cin>>x0>>y0>>xn>>yn;

double k,x=x0,y=y0;
int dx=xn-x0;
int dy=yn-y0;
k=max(dx,dy);

for(int i=0;i<k;i++){
cout<<x<<" "<<y<<" ";
    x+=(dx/k);
    y+=(dy/k);
 //进行取整运算
    x=int(x+0.5);
    y=int(y+0.5);
}

2、中点法

假设，最大位移方向为x方向，直线方程如下图所示。

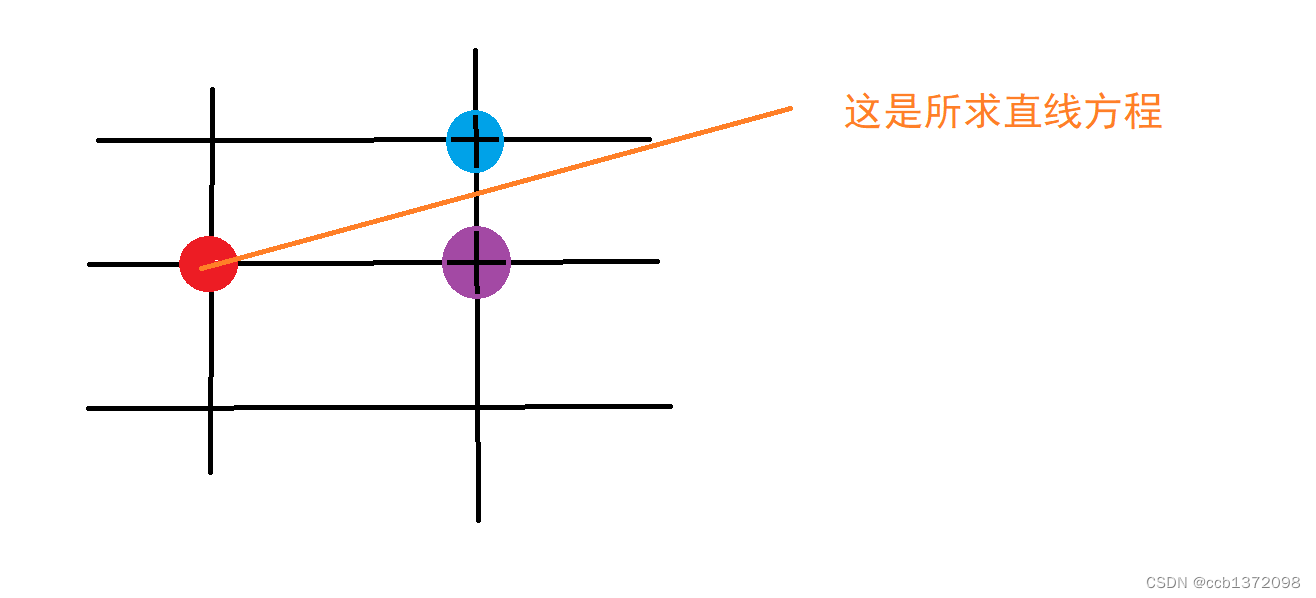
假设，红色点是我们现在位置，那么我们下一步，只能是走到蓝色点或者紫色点。紫色点$(x+1,y)$，蓝色点$(x+1,y+1)$。把紫色与蓝色中间的坐标$(x+1,y+0.5)$带入，再得解ym，判断ym的大小，ym>=0,下一个点为紫色点，否则为蓝色点。就这样算下去，直到结束。
$$\begin{gathered} ym>=0时，y{m}_{i+1}=y{m}_i+1-k \\ ym<0时，y{m}_{i+1}=y{m}_i-k \\ y{m}_0=0.5-k \\ 用2\Delta xy{m}_i替换y{m}_i \\ ym>=0,ym=ym+2\Delta x-2\Delta y \\ ym<0,ym=ym-2\Delta y \end{gathered}$$

int dx,dy,d,up,dow,x,y;
if(x0>xn){ //说明是第三象限
    //交换一下x0与xn即可，
    x=xn;
    xn=x0;
    x0=xn;
    
    y=yn;
    yn=y0;
    y0=y;  
}
dx=xn-x0;
dy=yn-y0;
x=x0;
y=y0;

d=dx-2*dy;
up=2*dx-2*dy;
dow=-2*dy;

//进行打印点
while(x<=xn){
    cout<<x<<y<<" ";
    ++x;
    if(d<0){  //说明是蓝色点
        ++y;
        d+=up;
    }else{  //说明是紫色点
        d+=dow;
    }
}

3、Bresenhan算法

这个算法是对中点法的优化。令e=$y{m}_i-0.5$,如果$e>0$说明下一个坐标是$(x+1,y+1)$否则就是$(x+1,y)$。为了除去小数(0.5)，用2e$\Delta x$来替换e。
$$\begin{gathered} e_{i+1}=\{\begin{array}{ll}{e}_i+2\Delta y-2\Delta x& e_i>0\\ e_i+2\Delta y& e_i\le 0\end{array} \\ e的初始值为-\Delta x \end{gathered}$$

int x,y,dx,dy,e;
dx=xn-x0;
dy=yn-y0;
e=-dx;
x=x0;y=y0;
while(x<=xn){
    cout<<x<<" "<<y<<" ";
    x++;
    e+=2*dy;
    if(e>0){
        y++;
        e-=2*dx;
    }
}

二、圆

1、中点Bresenham画圆算法

对于圆心不在原点的圆，可以通过平移，让它圆心变成原点。

由图可知，圆有4条对称轴，把圆分成了完全相同的8个圆，我们只需要画出1/8，就能画出完整的圆。

假设圆的方程
$$x^2+y^2=R^2$$
构造函数$F(x,y)=x^2+y^2-R^2$,

1. 对于圆上的点$F(x,y)=0$
2. 圆外的点$F(x,y)>0$
3. 圆内的点$F(x,y)<0$

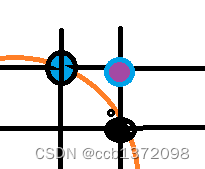
对于下一个点，在$(x+1，y),(x+1,y-1)$里面选一个，通过中点$(x+1,y+0.5)$的符合判断选择哪一个。
$$\begin{gathered} d_i=F(x+1,y+0.5)>0,选择(x+1,y-1); \\ {d}_i=F(x+1,y+0.5)\le 0,选择(x+1,y); \end{gathered}$$

$$\begin{gathered} d_{i+1}=\{\begin{array}{ll}{d}_i+2x_i+3,& d<0\\ d_i+2(x_i-y_i)+5,& d\ge 0\end{array} \\ d初始值为1-R \end{gathered}$$

int x,y,d;
x=0;
y=r;
d=1-r;
while(x<=r){
    cout<<x<<y<<" ";
    if(d<0){
        d+=2*x+3;
    }else{
        --y;
        d+=2(x-y)+5;
    }
    ++x;
}

2、椭圆的中点Bresenham算法

椭圆方程
$$F(x,y)=b^2{x}^2+a^2{y}^2-a^2{b}^2=0$$

由图可知，椭圆关于y=0,x=0对称，把椭圆分成了4个完全相等的部分。我们只需要画出1/4个即可,再利用对称性，就可画出全部。

把第一象限的椭圆分成2部分，如绿色和翠绿色，绿色最大位移方向为x方向，翠绿色最大位移方向为y方向。采用中点来判断下一个点在哪。

上部分（绿色），下一个点是$(x+1,y)或者(x+1,y-1)$.

下部分（翠绿色),下一个点是$(x,y-1)或者(x+1,y-1)$
$$构造判别式d_i=F(x+1,y+0.5)$$
上部分

$$d_{i+1}=\{\begin{array}{ll}{d}_i+b^2(2x_i+3),& d<0\\ d_i+b^2(2x_i+3)+a^2(-2y_i+2),& d\ge 0\end{array}$$
$$d初始值为b^2+a^2(-b+0.25)$$
下部分
$$d_{i+1}=\{\begin{array}{ll}{d}_i+b^2(2x_i+2)+a^2(-2y_i+3),& d<0\\ d_i+a^2(-2y_i+3),& d\ge 0\end{array}$$
$$d初始值为b^2(x+0.5{)}^2+a^2(y-1{)}^2-a^2{b}^2$$

int x,y;
double d1,d2;
x=0;
y=b;
d1=b*b+a*a*(-b+0.25);
cout<<x<<y<<" ";
cout<<-x<<-y<<" ";
cout<<-x<<y<<" ";
cout<<x<<-y<<" ";

//上半部分
while(b*b*(x+1)<a*a*(y-0.5)){
    if(d1<=0){
        d1+=b*b*(2*x+3);
        ++x;
    }else{
        d1+=b*b*(2*x+3)+a*a*(-2*y+2);
        ++x;
        --y;
    }
cout<<x<<y<<" ";
cout<<-x<<-y<<" ";
cout<<-x<<y<<" ";
cout<<x<<-y<<" ";  
}

//下半部
d2=b*b*(x+0.5)*(x+0.5)+a*a*(y-1)*(y-1)-a*a*b*b;
while(y<0){
    if(d2<=0){
        d2+=b*b*(2*x+2)+a*a*(-2*y+3);
        ++y;
        --y;
    }else{
        d2+=a*a*(-2*y+3);
        --y;
    }
cout<<x<<y<<" ";
cout<<-x<<-y<<" ";
cout<<-x<<y<<" ";
cout<<x<<-y<<" ";    
}