目录
- 数据结构
- 定义
- 数据结构的构成
- 逻辑结构
- 逻辑结构的类型
- 存储结构
- 数据运算
- 数据类型和抽象数据类型
- 算法
- 定义
- 分析基础
- 时间复杂度分析
- 事前分析估算法 -> 分析算法的执行时间
- 时间复杂度
- 时间复杂度类型
- 简化的算法时间复杂度分析
- 空间复杂度分析
数据结构
定义
-
数据:所有能够输入到计算机中,且能够被计算机处理的符号的集合。数据结构中主要讨论结构化数据,讨论的数据都是数据对象
-
结构化数据
- 数据元素:是数据(集合)中的一个“个体”,它是数据的基本单位
- 数据项:数据项是用来描述数据元素的,它是数据的最小单位
- 数据对象:具有相同性质的若干个数据元素的集合,如整数数据对象是所有整数的集合。
- 数据结构:是指带结构的数据元素的集合
数据结构 = 数据对象 + 结构
- 一个数据结构的构成
- 数据的逻辑结构:数据元素之间的逻辑关系
- 数据的存储结构/物理结构:数据元素及其关系在计算机存储器中的存储方式
- 数据运算:施加在该数据上的操作
数据结构的构成
逻辑结构
逻辑结构是面向用户的,有多种表示形式:表格、二元组、图形


逻辑结构的类型
- 集合
元素之间关系:无
特点:数据元素之间除了“属于同一个集合”的关系外,别无其他逻辑关系。是最松散的,不受任何制约的关系。

2. 线性结构
元素之间关系:一对一
特点:开始元素和终端元素都是唯一的,除此之外,其余元素都有且只有一个前驱元素和一个后继元素。

3. 树形结构
元素之间关系:一对多
特点:开始元素唯一,终端元素不唯一。除终端元素以外,每个元素有一个或多个后续元素;除开始元素外,每个元素有且仅有一个前驱元素。
4. 图形结构
元素之间关系:多对多
特点:所有元素都可能有多个前驱元素和多个后继元素。
存储结构
数据在计算机存储器中的存储方式就是存储结构,满足两个要求:存储所有元素;存储数据元素间的关系
- 结构体数组(顺序存储结构):所有元素占用一整块内存空间;逻辑上相邻的元素,物理上也相邻
- 链表(链式存储结构):一个逻辑元素用一个节点存储,每个节点单独分配,所有节点的地址不一定是连续的;用指针来表示逻辑关系
- 索引存储结构
- 哈希(散列)存储结构
数据运算
数据运算是对数据的操作。分为两个层次:运算描述和运算实现
结论:
同一逻辑结构可以对应多种存储结构
同样的运算,在不同的存储结构中,其实现过程是不同的
数据类型和抽象数据类型
- 数据类型是一个值的集合和定义在此集合上的一组操作的总称,就是已经实现了的数据结构(比如int整数类型等)
- 抽象数据类型(ADT):指的是从求解问题的数学模型中抽象出来的数据逻辑结构和运算(抽象运算),而不考虑计算机的具体实现**(抽象数据类型 = 逻辑结构 + 抽象运算)**
//定义复数抽象数据类型 Complex,一个复数的形式:e1+e2i
ADT Complex
{
D={e1,e2|e1,e2均为实数} //数据对象
R{<e1,e2>|e1是复数的实部,e2是复数的虚部} //数据关系
}
基本运算:

算法
定义
- 定义
- 数据元素之间的关系有逻辑关系和物理关系,对应的运算有基于逻辑结构的运算描述和基于存储结构的运算实现。
- 通常把基于存储结构的运算实现步骤或过程称为算法。
- 算法的五个重要的特性
| 特性 | 内容 |
|---|---|
| 有穷性 | 在有穷步之后结束,算法能够停机 |
| 确定性 | 算法中的每一条指令必须有确定的含义,无二义性 |
| 可行性 | 可通过基本运算有限次执行来实现,也就是算法中每一个动作能够被机械地执行 |
| 有输入 | 一个算法有0个或多个输入 |
| 有输出 | 一个算法有1个或多个输出 |
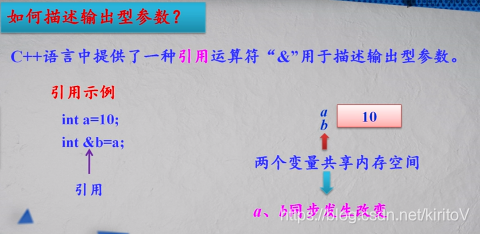
- 如何描述输出型参数
分析基础
分析算法占用的资源
- CPU时间->时间复杂度
- 内存空间->空间复杂度
时间复杂度分析
一个算法是由 控制结构(顺序、分支和循环三种) 和 原操作(指固有数据类型的操作,如+、-、*、/、++、–等) 构成。算法执行时间取决于两者的总和效果。

2. 两种衡量算法效率的方法:事后统计法和事前分析估算法。
事前分析估算法 -> 分析算法的执行时间
- 求出算法所有原操作的执行次数(也称为频度),它是问题规模n(用于表示求解问题大小的正整数,如n个记录排序)的函数,用T(n)表示
- 算法执行时间大致 = 原操作所需时间 x T(n),所以T(n)与算法的执行时间成正比。为此用T(n)表示算法的执行时间
- 比较不同算法的T(n)大小得出算法执行时间的好坏
时间复杂度
- 算法的执行时间用时间复杂度来表示。
- 算法中执行时间T(n) 是 问题规模n的某个函数f(n),记作:T(n) = O(f(n))。记号“O”读作 “大O” ,它表示问题规模n的增大算法执行时间的增长率和f(n)的 增长率相同。
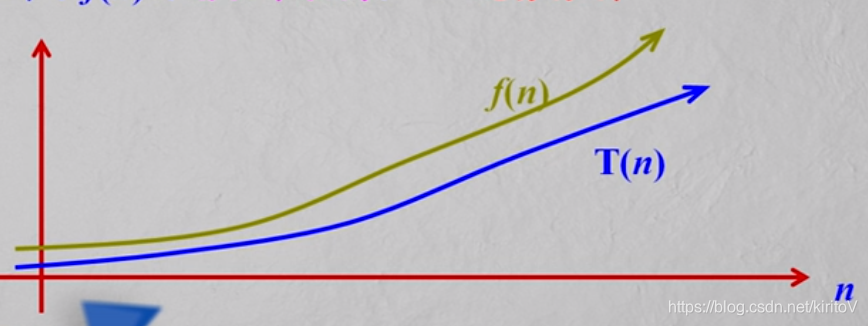
- “O”的形式定义:
T(n) = O(f(n)) 表示存在一个正的常数M,使得当n>=n0时都满足:|T(n)| <= M|f(n)|,f(n)是T(n)的上界,通常取最接近的上界,即紧凑上界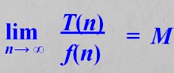
- 就是只求出T(n)的最高阶,忽略其低阶项和常系数,这样既可以简化T(n)的计算,又能够比较客观的反映出当n很大时算法的时间性能。
时间复杂度类型
- 一个没有循环的算法的执行时间与问题规模n无关,记作O(1),也称作常数阶;
- 一个只有一重循环的算法的执行时间与问题规模n的增长呈线性增长关系,记作O(n),也称作线性阶;
- 其余常用的算法时间复杂度还有平方阶O(n2)、立方阶O(n3)、对数阶O(log2n)、指数阶O(2n)等;

例子:
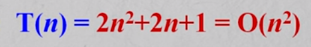
简化的算法时间复杂度分析
- 算法中的基本操作一般是最深层循环内的原操作
- 算法执行时间大致=基本操作时间所需的时间 x 其运算次数
总结:在算法分析时,计算T(n)时仅仅考虑基本操作的运算次数。
空间复杂度分析
- 空间复杂度:用于亮度一个算法在运行过程中临时占用的存储空间的大小
- 一般也作为问题规模n的函数,采用数量级形式描述,记作:S(n) = O(g(n))
- 若一个算法的空间复杂度为O(1),则称此算法为原地工作/就地工作算法