算法效率

我们在算法的设计中，会去衡量算法的好坏。那么算法效率就是衡量标准之一。除此之外，我们也会关注到算法的健壮性、正确性、可读性、效率与低存储量的要求。这里的效率和低存储量要求可以引入两个名词，时间复杂度和空间复杂度。通俗来讲，效率指的是算法执行时间。对于同一个问题如果有多个算法可以解决，执行时间短的算法效率高。存储量需求指算法执行过程中所需要的最大存储空间。效率与低存储量需求这两者都与问题的规模有关。

时间复杂度

时间复杂度的定义

一般情况下，算法中基本操作重复执行的次数是为题规模n的某个函数 f(n)
,算法的时间量度记作$$T(n)=O(f(n)）$$ 它表示随问题规模n的增大，算法执行时间的增长率和f(n)的增长率相同，称作算法的渐进时间复杂度，简称时间复杂度
我们来进行实操

// 请计算一下Func1中++count语句总共执行了多少次？
void Func1(int N)
{
int count = 0;
for (int i = 0; i < N ; ++ i)
{
 	for (int j = 0; j < N ; ++ j)
$$ 	{
 		++count;
 	}
}
 
for (int k = 0; k < 2 * N ; ++ k)
{
 	++count;
}
int M = 10;
while (M--)
{
 	++count;
}
printf("%d\n", count);

算出来的结果是：
$$F(N)=N^2+2N+M$$

实际中我们计算时间复杂度时，我们其实并不一定要计算精确的执行次数，而只需要大概执行次数，那么这 里我们使用大O的渐进表示法。

大O渐进渐进表示法

大O符号（Big O notation）：是用于描述函数渐进行为的数学符号。
推导大O阶方法：
1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中，只保留最高阶项。
3、如果最高阶项存在且不是1，则去除与这个项目相乘的常数。得到的结果就是大O阶。
使用大O的渐进表示法以后，Func1的时间复杂度为:
$$O(N^2)$$
通过上面我们会发现大O的渐进表示法去掉了那些对结果影响不大的项，简洁明了的表示出了执行次数。
另外有些算法的时间复杂度存在最好、平均和最坏情况：
最坏情况：任意输入规模的最大运行次数(上界)
平均情况：任意输入规模的期望运行次数
最好情况：任意输入规模的最小运行次数(下界)
例如：在一个长度为N数组中搜索一个数据x
最好情况：1次找到
最坏情况：N次找到
平均情况：N/2次找到
在实际中一般情况关注的是算法的最坏运行情况，所以数组中搜索数据时间复杂度为O(N)

常见的时间复杂度计算举例

void Func2(int N)
{
	int count = 0;
	for (int k = 0; k < 2 * N; ++k)
	{
		++count;
	}
	int M = 10;
	while (M--)
	{
		++count;
	}
	printf("%d\n", count);
}
// 计算Func3的时间复杂度？
void Func3(int N, int M)
{
	int count = 0;
	for (int k = 0; k < M; ++k)
	{
		++count;
	}
	for (int k = 0; k < N; ++k)
	{
		++count;
	}
	printf("%d\n", count);
}

Func2 的第一个循环会执行2N次，第二个循环会执行M次， Func2 的时间复杂度为: 2N+M, 用大O渐进表示法得：
$$O(N)$$
Func3 的第一个循环执行了M次，第二个循环执行了N次，Func3的时间复杂度为: M+N ,用大O渐进法表示法得：
$$O(M+N)$$
这里除非是题目中规定了N比M大，那么N的影响是最大的。时间复杂度为:
$$O(N)$$

const char * strchr ( const char * str, int character );

这是一个C语言的库函数，它的作用是返回一个字符在字符串中的位置。并且返回这个字符的起始位置，我们可以去这样实现:

const char* my_strchr(const char* str, int character)
{
	while (*str)
	{
		if (*str == character)
		{
			return str;
		}
		str++;
	}
}

对于这个算法的时间复杂度，取决于字符串的大小，因为字符串越长遍历次数越多。还取决于character的位置，character越在字符串的后面，遍历次数越多，语句的执行次数也就相应的增加了。
这个算法的时间复杂度为:
$$O(N)$$

// 计算BubbleSort的时间复杂度？
void BubbleSort(int* a, int n)
{
 	assert(a);
 	for (size_t end = n; end > 0; --end)
 	{
 		int exchange = 0;
 		for (size_t i = 1; i < end; ++i)
 		{
 			if (a[i-1] > a[i])
 			{
 				Swap(&a[i-1], &a[i]);
 				exchange = 1;
			}
	 	}
 		if (exchange == 0)
 			break;
 	}
}

冒泡排序在执行的过程中，第一次循环需要执行n-1次，第二次执行n-2次，第三次执行n-3次，第四次执行n-4次……一直到执行1次。把所有的执行次数加起来，这是一个等差数列。可以算出语句的频度为 n*(n-1)/2次。用大O渐进表示法表示:
$$O(N^2)$$

// 计算BinarySearch的时间复杂度？
int BinarySearch(int* a, int n, int x)
{
 	assert(a);
 	int begin = 0;
 	int end = n-1;
 	// [begin, end]：begin和end是左闭右闭区间，因此有=号
	 while (begin <= end)
 	{
 		int mid = begin + ((end-begin)>>1);
 		if (a[mid] < x)
 			begin = mid+1;
		else if (a[mid] > x)
 			end = mid-1;
 		else
 			return mid;
 	}
 	return -1;
}

这个算法为二分查找算法，比如有N个数据，要查找数据的最差的情况是在这串数据的最前边和最后边，那么我们必须把mid移到那一个想要查找的数据上面，所以,假如循环执行了x次。那么，N = 2^x，也就是x个2相乘=N ，语句的执行频度为 x = log以2为底N的对数。用大O渐进表示法可表示为；
$$O(logN)$$

// 计算阶乘递归Fac的时间复杂度？
long long Fac(size_t N)
{
 	if(0 == N)
 		return 1;
 
 	return Fac(N-1)*N;
}

我们可以知道以上的程序是求N的阶乘的递归算法，那么我们就要算出他递归了几次，就可以算出它的时间复杂度。分析: 当N = 3 的时候，我们可以拆解为，$$3\ast Fac(2\ast Fac(1\ast Fac(0)))$$
我们可以看到，这个算法递归了N次，所以用大O渐进表示法可以表示为$$O(N)$$

// 计算斐波那契递归Fib的时间复杂度？
long long Fib(size_t N)
{
 if(N < 3)
 return 1;
 
 return Fib(N-1) + Fib(N-2);
}

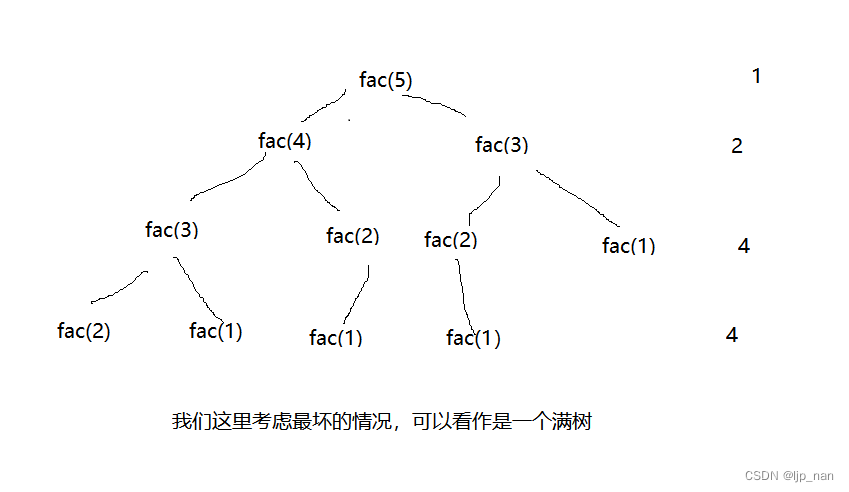
我们可以使用二叉树的性质来做这道题，考虑最坏的情况，这个二叉树的是一个满二叉树，那么它的最大节点个数为:
$$2^k-1$$ 个，其中k表示深度。那么它的递归次数就是 $$2^k-1$$次。然后用大O渐进表示法可以表示为$$O(2^k)$$
具体可以看这个图，我们假如N 为5。
3>

空间复杂度

空间复杂度也是一个数学表达式，是对一个算法在运行过程中临时占用存储空间大小的量度 。
空间复杂度不是程序占用了多少bytes的空间，因为这个也没太大意义，所以空间复杂度算的是变量的个数。
空间复杂度计算规则基本跟实践复杂度类似，也使用大O渐进表示法。
注意：函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了，因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。
比如: 冒泡排序的空间复杂度： 它在执行的时候只开辟了一块临时的辅助空间。使用了常数个辅助空间，空间复杂度为: $$O(1)$$

// 计算Fibonacci的空间复杂度？
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n)
{
 	if(n==0)
		return NULL;
 
 	long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));
 	fibArray[0] = 0;
 	fibArray[1] = 1;
 	for (int i = 2; i <= n ; ++i)
 	{
		fibArray[i] = fibArray[i - 1] + fibArray [i - 2];
 	}
 	return fibArray;
}

实例2动态开辟了N个空间，空间复杂度为 O(N)

// 计算阶乘递归Fac的空间复杂度？
long long Fac(size_t N)
{
 	if(N == 0)
		 return 1;
 
 	return Fac(N-1)*N;
}

实例3递归调用了N次，开辟了N个栈帧，每个栈帧使用了常数个空间。空间复杂度为O(N)