如有错误,感谢不吝赐教、交流
文章目录
- 背景描述
- 实现方法
- 一、寻找两组合的最优
- 二、基于两组合的最优结果寻找四组合最优
- 三、基于四组合的最优结果寻找八组合最优
- 四、基于八组合的最优结果寻找十六组合最优
- 总结
- 适用场景
背景描述
假如list = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127, 128, 129, 130, 131, 132, 133, 134, 135, 136, 137, 138, 139, 140, 141, 142, 143, 144, 145, 146, 147, 148, 149, 150, 151, 152, 153, 154, 155, 156, 157, 158, 159] 是一个160个索引的集合,每个索引对应一条具体数据,如图片或其他,现在我们需要将这个160长度的数据寻找按照每16个组合在一起的最优结果,即将list按照16为一组分成10组,要求最后分类最佳(如图片,即要求每组内图片最相似)
最优组合计算:
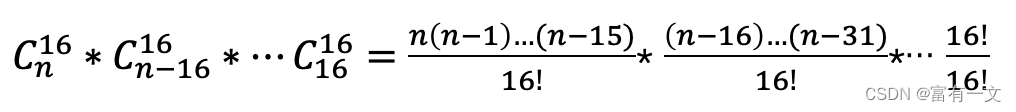
需要从如此多的组合中去寻找一个最优解组合,显然不现实
通过每次取最优组合再组合,逼近最优解组合,探索数组组合能提升的一个“可能上限”(不是绝对上限,无法求最优解组合)
实现方法
一、寻找两组合的最优
首先,同上文找16组合最优解不可求,2组合最优解同样不可求
2组合最优解计算:
解决策略:
1、每次取当下最优2组合
2、总的数据list中去掉该2组合
3、重复操作1、操作2,直到总的数据list长度为0
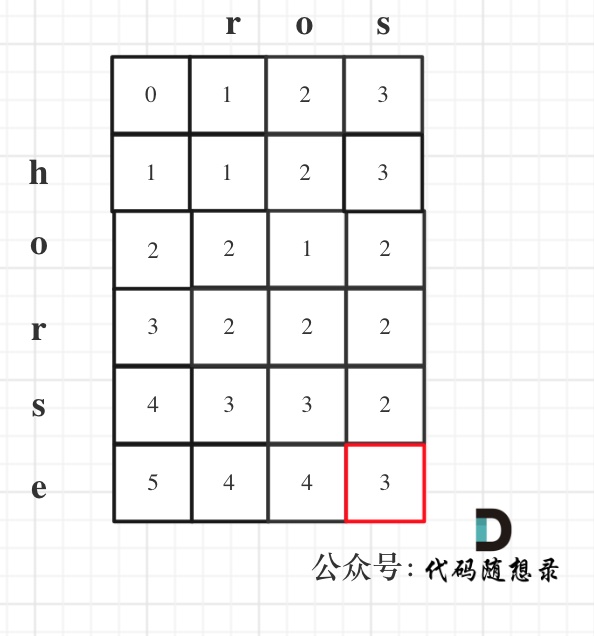
如下所示:
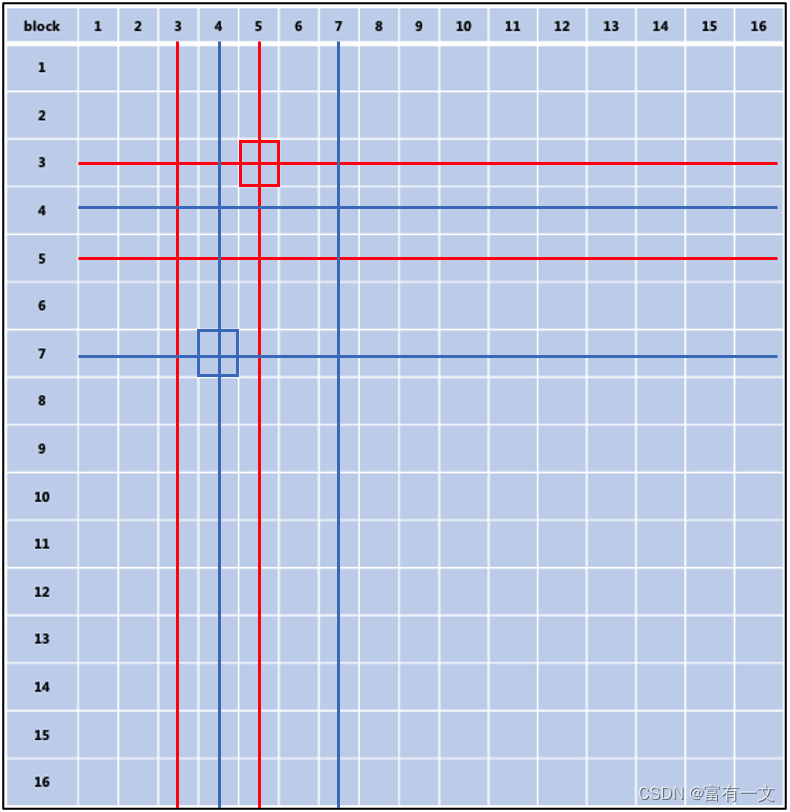
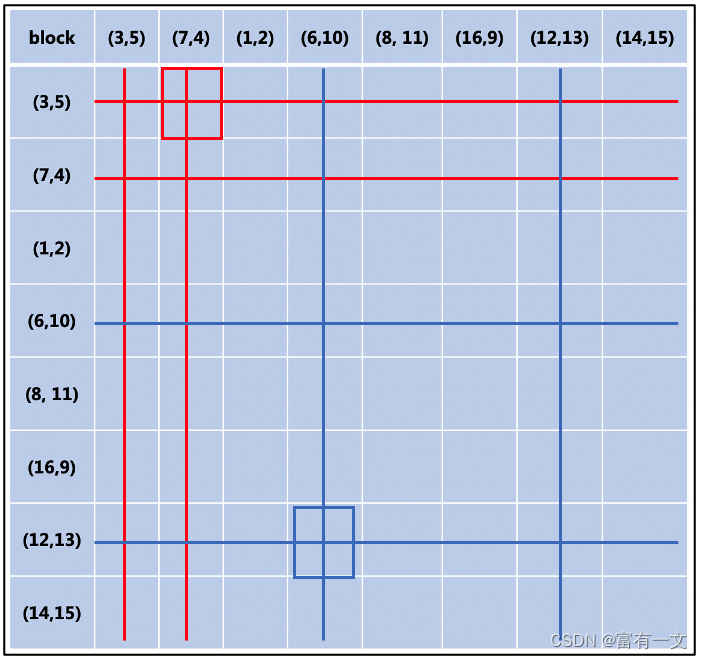
1.若(3, 5)组合最大,如红线所示去掉相关元素
2.剩下元素中搜索,若(7, 4)组合最大,同操作1一样去除,如图中蓝线所示
3.重复执行,直到去除组合矩阵中所有元素
不同应用代码不同,以下所示为我需要计算数据块A和数据块B,求组合压缩最大的结果的贪心搜索代码:
# 获取二组合结果
def get_two_result(data_path, use_data, cctx, length_2=8192 * 2):
count = 1
length = len(use_data)
flag = [0] * length
total_length_2 = 0
result_2 = []
csv_path = "./result/{}_greed_2_{}.csv".format(data_path.split('/')[-1].split('.')[0], length) # 存储结果路径
compress_result_2 = [] # 存储所有的组合2个数据块 组合
s_time = time.time()
## 核心:生成组合矩阵
for i in range(length):
print("第{}次计算压缩比矩阵".format(i + 1))
for j in range(length):
if i != j:
compress_length = len(cctx.compress(use_data[i] + use_data[j]))
compress_rito = 8192 * 2 / compress_length
compress_result_2.append([i, j, compress_rito, compress_length])
print("组合计算完毕,总用时:{}s,开始贪心搜索".format(time.time() - s_time))
## 核心:每次取当下最优
while len(compress_result_2) != 0:
print("第{}计算开始".format(count))
start_time = time.time()
compress_result_2.sort(key=lambda x: x[2], reverse=True) # 根据压缩比排序
flag[compress_result_2[0][0]] = 1
flag[compress_result_2[0][1]] = 1
total_length_2 += compress_result_2[0][3] # 两个合并压缩的长度
result_2.append(
[compress_result_2[0][0], compress_result_2[0][1], compress_result_2[0][2], compress_result_2[0][3]])
compress_result_2 = array_diff2(compress_result_2, flag)
print("第{}计算结束,用时{}".format(count, time.time() - start_time))
count += 1
# 计算base_2压缩比
base_2_data = load_data_length(data_path, length_2)
base_2_use_data = base_2_data[:(length // 2)]
base_2_total = 0
for i in base_2_use_data:
base_2_total += len(cctx.compress(i))
base_2_com_rito = 8192 * length / base_2_total
# 结果入表
print("结果入表开始")
with open(csv_path, mode='w') as csvfile:
writer = csv.writer(csvfile)
writer.writerow(['index_1', 'index_2', "Com_Rito", "Com_len"])
for i in result_2:
writer.writerow([i[0], i[1], i[2], i[3]])
writer.writerow(['贪心总压缩长度', total_length_2])
greed_2 = round(8192 * len(use_data) / total_length_2, 4)
writer.writerow(['greed_2', greed_2])
base_2 = round(base_2_com_rito, 4)
writer.writerow(['base_2', base_2])
gain = round((greed_2 - base_2) / base_2, 4)
writer.writerow(['gain', gain])
print("结果入表完成")
return result_2, total_length_2, gain, csv_path
核心:
生成组合矩阵
每次取当下最优
去除在b集合中标记为1对应的a集合中的数据
a集合为对应的list的组合矩阵结果,b集合为标记集合,使用了的索引对应位置标记为1,以此去掉a集合中使用后的索引,后面提到的都是这个意思
def array_diff2(a, b):
return [x for x in a if b[x[0]] != 1 and b[x[1]] != 1]
以下原理类推
二、基于两组合的最优结果寻找四组合最优
同理四组合最优也是不可解的
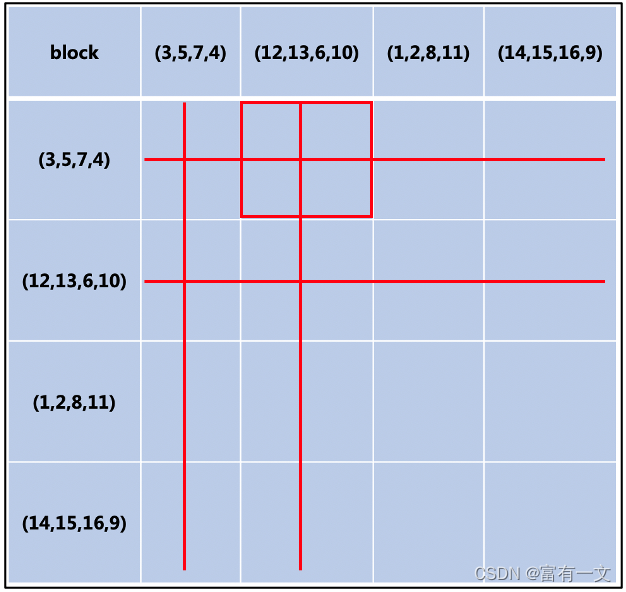
1.若(3,5, 7,4)组合最大,如红线所示去掉相关元素
2.剩下元素中搜索,若(12,13,6, 10)组合最大,同操作1一样去除,如图中蓝线所示
3.重复执行,直到去除组合矩阵中所有元素
def array_diff4(a, b):
return [x for x in a if b[x[0]] != 1 and b[x[1]] != 1 and b[x[2]] != 1 and b[x[3]] != 1]
# # 获取四组合结果
def get_four_result(data_path, use_data, cctx, result_2_path, length_4=8192 * 4):
count = 1
length = len(use_data)
flag = [0] * length
total_length_4 = 0
result_4 = [] # 存储四个组合的返回结果
csv_path = "./result/{}_greed_4_{}.csv".format(data_path.split('/')[-1].split('.')[0], length) # 存储结果路径
s_time = time.time()
compress_result_2 = []
with open(result_2_path, "r") as f:
lines = f.readlines()[1: (length // 2) + 1]
for line in lines:
x = line.split(",")
compress_result_2.append([int(x[0]), int(x[1])])
compress_result_4 = [] # 存储所有的四组合数据块的压缩矩阵
for i in range(length // 2):
print("第{}次计算压缩比矩阵".format(i + 1))
for j in range(length // 2):
if i != j:
compress_length = len(cctx.compress(use_data[compress_result_2[i][0]]
+ use_data[compress_result_2[i][1]]
+ use_data[compress_result_2[j][0]]
+ use_data[compress_result_2[j][1]]
))
compress_rito = 8192 * 4 / compress_length
compress_result_4.append([compress_result_2[i][0],
compress_result_2[i][1],
compress_result_2[j][0],
compress_result_2[j][1],
compress_rito,
compress_length]
)
print("组合计算完毕,总用时:{}s,开始贪心搜索".format(time.time() - s_time))
while len(compress_result_4) != 0:
print("第{}计算开始".format(count))
start_time = time.time()
compress_result_4.sort(key=lambda x: x[4], reverse=True) # 根据压缩比排序
flag[compress_result_4[0][0]] = 1
flag[compress_result_4[0][1]] = 1
flag[compress_result_4[0][2]] = 1
flag[compress_result_4[0][3]] = 1
total_length_4 += compress_result_4[0][5] # 四个合并压缩的长度
result_4.append(
[compress_result_4[0][0],
compress_result_4[0][1],
compress_result_4[0][2],
compress_result_4[0][3],
compress_result_4[0][4],
compress_result_4[0][5]])
compress_result_4 = array_diff4(compress_result_4, flag)
print("第{}计算结束,用时{}".format(count, time.time() - start_time))
count += 1
# 计算base_2压缩比
base_4_data = load_data_length(data_path, length_4)
base_4_use_data = base_4_data[:(length // 4)]
base_4_total = 0
for i in base_4_use_data:
base_4_total += len(cctx.compress(i))
base_4_com_rito = 8192 * length / base_4_total
# 结果入表
print("结果入表开始")
with open(csv_path, mode='w') as csvfile:
writer = csv.writer(csvfile)
writer.writerow(['index_1', 'index_2', 'index_3', 'index_4', "Com_Rito", "Com_len"])
for i in result_4:
writer.writerow([i[0], i[1], i[2], i[3], i[4], i[5]])
writer.writerow(['贪心总压缩长度', total_length_4])
greed_4 = round(8192 * length / total_length_4, 4)
writer.writerow(['greed_4', greed_4])
base_4 = round(base_4_com_rito, 4)
writer.writerow(['base_4', base_4])
gain = round((greed_4 - base_4) / base_4, 4)
writer.writerow(['gain', gain])
print("结果入表完成")
return result_4, total_length_4, gain, csv_path
三、基于四组合的最优结果寻找八组合最优
同理八组合最优也是不可解的
解决策略
1.若(3,5, 7,4, 12,13,6, 10)压缩比最大,如红线所示去掉相关元素
2.重复执行,直到去除压缩比组合矩阵中所有元素
def array_diff8(a, b):
return [x for x in a
if b[x[0]] != 1
and b[x[1]] != 1
and b[x[2]] != 1
and b[x[3]] != 1
and b[x[4]] != 1
and b[x[5]] != 1
and b[x[6]] != 1
and b[x[7]] != 1
]
# # 获取八组合结果
def get_eight_result(data_path, use_data, cctx, result_4_path, length_8=8192 * 8):
count = 1
length = len(use_data)
flag = [0] * length
total_length_8 = 0
result_8 = [] # 存储八个组合的返回结果
csv_path = "./result/{}_greed_8_{}.csv".format(data_path.split('/')[-1].split('.')[0], length) # 存储结果路径
s_time = time.time()
compress_result_4 = []
with open(result_4_path, "r") as f:
lines = f.readlines()[1: (length // 4) + 1]
for line in lines:
x = line.split(",")
compress_result_4.append([int(x[0]), int(x[1]), int(x[2]), int(x[3])])
compress_result_8 = [] # 存储所有的八组合数据块的压缩矩阵
for i in range(length // 4):
print("第{}次计算压缩比矩阵".format(i + 1))
for j in range(length // 4):
if i != j:
compress_length = len(cctx.compress(use_data[compress_result_4[i][0]]
+ use_data[compress_result_4[i][1]]
+ use_data[compress_result_4[i][2]]
+ use_data[compress_result_4[i][3]]
+ use_data[compress_result_4[j][0]]
+ use_data[compress_result_4[j][1]]
+ use_data[compress_result_4[j][2]]
+ use_data[compress_result_4[j][3]]
))
compress_rito = 8192 * 8 / compress_length
compress_result_8.append([compress_result_4[i][0],
compress_result_4[i][1],
compress_result_4[i][2],
compress_result_4[i][3],
compress_result_4[j][0],
compress_result_4[j][1],
compress_result_4[j][2],
compress_result_4[j][3],
compress_rito,
compress_length]
)
print("组合计算完毕,总用时:{}s,开始贪心搜索".format(time.time() - s_time))
while len(compress_result_8) != 0:
print("第{}计算开始".format(count))
start_time = time.time()
compress_result_8.sort(key=lambda x: x[8], reverse=True) # 根据压缩比排序
flag[compress_result_8[0][0]] = 1
flag[compress_result_8[0][1]] = 1
flag[compress_result_8[0][2]] = 1
flag[compress_result_8[0][3]] = 1
flag[compress_result_8[0][4]] = 1
flag[compress_result_8[0][5]] = 1
flag[compress_result_8[0][6]] = 1
flag[compress_result_8[0][7]] = 1
total_length_8 += compress_result_8[0][9] # 八个合并压缩的长度
result_8.append(
[compress_result_8[0][0],
compress_result_8[0][1],
compress_result_8[0][2],
compress_result_8[0][3],
compress_result_8[0][4],
compress_result_8[0][5],
compress_result_8[0][6],
compress_result_8[0][7],
compress_result_8[0][8],
compress_result_8[0][9]])
compress_result_8 = array_diff8(compress_result_8, flag)
print("第{}计算结束,用时{}".format(count, time.time() - start_time))
count += 1
# 计算base_8压缩比
base_8_data = load_data_length(data_path, length_8)
base_8_use_data = base_8_data[:(length // 8)]
base_8_total = 0
for i in base_8_use_data:
base_8_total += len(cctx.compress(i))
base_8_com_rito = 8192 * length / base_8_total
# 结果入表
print("结果入表开始")
with open(csv_path, mode='w') as csvfile:
writer = csv.writer(csvfile)
writer.writerow(
['index_1', 'index_2', 'index_3', 'index_4', 'index_5', 'index_6', 'index_7', 'index_8', "Com_Rito",
"Com_len"])
for i in result_8:
writer.writerow([i[0], i[1], i[2], i[3], i[4], i[5], i[6], i[7], i[8], i[9]])
writer.writerow(['贪心总压缩长度', total_length_8])
greed_8 = round(8192 * length / total_length_8, 4)
writer.writerow(['greed_8', greed_8])
base_8 = round(base_8_com_rito, 4)
writer.writerow(['base_8', base_8])
gain = round((greed_8 - base_8) / base_8, 4)
writer.writerow(['gain', gain])
print("结果入表完成")
return result_8, total_length_8, gain, csv_path
四、基于八组合的最优结果寻找十六组合最优
def array_diff16(a, b):
return [x for x in a
if b[x[0]] != 1
and b[x[1]] != 1
and b[x[2]] != 1
and b[x[3]] != 1
and b[x[4]] != 1
and b[x[5]] != 1
and b[x[6]] != 1
and b[x[7]] != 1
and b[x[8]] != 1
and b[x[9]] != 1
and b[x[10]] != 1
and b[x[11]] != 1
and b[x[12]] != 1
and b[x[13]] != 1
and b[x[14]] != 1
and b[x[15]] != 1
]
# # 获取16组合结果
def get_sixteen_result(data_path, use_data, cctx, result_8_path, length_16=8192 * 16):
count = 1
length = len(use_data)
flag = [0] * length
total_length_16 = 0
result_16 = [] # 存储16个组合的返回结果
csv_path = "./result/{}_greed_16_{}.csv".format(data_path.split('/')[-1].split('.')[0], length) # 存储结果路径
s_time = time.time()
compress_result_8 = []
with open(result_8_path, "r") as f:
lines = f.readlines()[1: (length // 8) + 1]
for line in lines:
x = line.split(",")
compress_result_8.append(
[int(x[0]), int(x[1]), int(x[2]), int(x[3]), int(x[4]), int(x[5]), int(x[6]), int(x[7])])
compress_result_16 = [] # 存储所有的16组合数据块的压缩矩阵
for i in range(length // 8):
print("第{}次计算压缩比矩阵".format(i + 1))
for j in range(length // 8):
if i != j:
compress_length = len(cctx.compress(use_data[compress_result_8[i][0]]
+ use_data[compress_result_8[i][1]]
+ use_data[compress_result_8[i][2]]
+ use_data[compress_result_8[i][3]]
+ use_data[compress_result_8[i][4]]
+ use_data[compress_result_8[i][5]]
+ use_data[compress_result_8[i][6]]
+ use_data[compress_result_8[i][7]]
+ use_data[compress_result_8[j][0]]
+ use_data[compress_result_8[j][1]]
+ use_data[compress_result_8[j][2]]
+ use_data[compress_result_8[j][3]]
+ use_data[compress_result_8[j][4]]
+ use_data[compress_result_8[j][5]]
+ use_data[compress_result_8[j][6]]
+ use_data[compress_result_8[j][7]]
))
compress_rito = 8192 * 16 / compress_length
compress_result_16.append([compress_result_8[i][0],
compress_result_8[i][1],
compress_result_8[i][2],
compress_result_8[i][3],
compress_result_8[i][4],
compress_result_8[i][5],
compress_result_8[i][6],
compress_result_8[i][7],
compress_result_8[j][0],
compress_result_8[j][1],
compress_result_8[j][2],
compress_result_8[j][3],
compress_result_8[j][4],
compress_result_8[j][5],
compress_result_8[j][6],
compress_result_8[j][7],
compress_rito,
compress_length]
)
print("组合计算完毕,总用时:{}s,开始贪心搜索".format(time.time() - s_time))
while len(compress_result_16) != 0:
print("第{}计算开始".format(count))
start_time = time.time()
compress_result_16.sort(key=lambda x: x[16], reverse=True) # 根据压缩比排序
flag[compress_result_16[0][0]] = 1
flag[compress_result_16[0][1]] = 1
flag[compress_result_16[0][2]] = 1
flag[compress_result_16[0][3]] = 1
flag[compress_result_16[0][4]] = 1
flag[compress_result_16[0][5]] = 1
flag[compress_result_16[0][6]] = 1
flag[compress_result_16[0][7]] = 1
flag[compress_result_16[0][8]] = 1
flag[compress_result_16[0][9]] = 1
flag[compress_result_16[0][10]] = 1
flag[compress_result_16[0][11]] = 1
flag[compress_result_16[0][12]] = 1
flag[compress_result_16[0][13]] = 1
flag[compress_result_16[0][14]] = 1
flag[compress_result_16[0][15]] = 1
total_length_16 += compress_result_16[0][17] # 17个合并压缩的长度
result_16.append(
[compress_result_16[0][0],
compress_result_16[0][1],
compress_result_16[0][2],
compress_result_16[0][3],
compress_result_16[0][4],
compress_result_16[0][5],
compress_result_16[0][6],
compress_result_16[0][7],
compress_result_16[0][8],
compress_result_16[0][9],
compress_result_16[0][10],
compress_result_16[0][11],
compress_result_16[0][12],
compress_result_16[0][13],
compress_result_16[0][14],
compress_result_16[0][15],
compress_result_16[0][16],
compress_result_16[0][17]])
compress_result_16 = array_diff16(compress_result_16, flag)
print("第{}计算结束,用时{}".format(count, time.time() - start_time))
count += 1
# 计算base_16压缩比
base_16_data = load_data_length(data_path, length_16)
base_16_use_data = base_16_data[:(length // 16)]
base_16_total = 0
for i in base_16_use_data:
base_16_total += len(cctx.compress(i))
base_16_com_rito = 8192 * length / base_16_total
# 结果入表
print("结果入表开始")
with open(csv_path, mode='w') as csvfile:
writer = csv.writer(csvfile)
writer.writerow(
['index_1',
'index_2',
'index_3',
'index_4',
'index_5',
'index_6',
'index_7',
'index_8',
'index_9',
'index_10',
'index_11',
'index_12',
'index_13',
'index_14',
'index_15',
'index_16',
"Com_Rito",
"Com_len"])
for i in result_16:
writer.writerow([i[0], i[1], i[2], i[3], i[4], i[5], i[6], i[7], i[8], i[9],
i[10], i[11], i[12], i[13], i[14], i[15], i[16], i[17]])
writer.writerow(['贪心总压缩长度', total_length_16])
greed_16 = round(8192 * length / total_length_16, 4)
writer.writerow(['greed_16', greed_16])
base_16 = round(base_16_com_rito, 4)
writer.writerow(['base_16', base_16])
gain = round((greed_16 - base_16) / base_16, 4)
writer.writerow(['gain', gain])
print("结果入表完成")
return result_16, total_length_16, gain
总结
通过不断地获得2组合最优,4组合最优,8组合最优,16组合最优,贪心的逼近16组合的最优解,当然这个过程中获得的结果一定不是16组合最优解,但是能在一定程度上体现16组合最优解的接近上限,以此判断当前任务,寻找16相似组合有没有实施的必要。
适用场景
已知n个图片,当把相似图片放在一起,压缩结果会更好,最大只能16张图片组合。求方法以使得能寻找到相似的图片放到一起压缩。
此场景下,需要判断将最相似的最优解放在一起压缩的上限是多少,但是无法获得最优解,即可通过上述办法,逼近最优解的组合结果。
ps:计划每日更新一篇博客,今日2023-04-17,日更第一天。