一、题目

🔸题目描述

Levenshtein 距离，又称编辑距离，指的是两个字符串之间，由一个转换成另一个所需的最少编辑操作次数。许可的编辑操作包括将一个字符替换成另一个字符，插入一个字符，删除一个字符。编辑距离的算法是首先由俄国科学家 Levenshtein 提出的，故又叫 Levenshtein Distance 。
例如：
字符串A: abcdefg
字符串B: abcdef
通过增加或是删掉字符 ”g” 的方式达到目的。这两种方案都需要一次操作。把这个操作所需要的次数定义为两个字符串的距离。
要求：
给定任意两个字符串，写出一个算法计算它们的编辑距离。

🔸输入输出

输入
每组用例一共2行，为输入的两个字符串

输出
每组用例输出一行，代表字符串的距离

🔸样例1

输入
abcdefg
abcdef



输出
1

二、思路解析

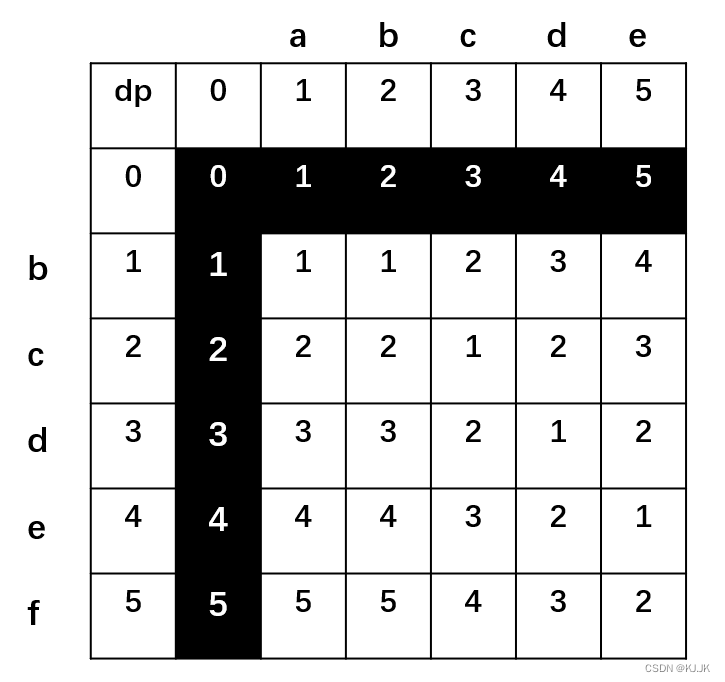
编辑距离是一类非常经典的动态规划的题目。我们使用dp[i][j]表示字符串A的前i个字符与字符串B的前j个字符相同所需要的编辑距离。首先需要进行状态的初始化，当一个字符串为空时，编辑距离等于另一个字符串的长度对于状态转移方程，需要分两种情况讨论：第一种情况，a[i]==b[j]，这种情况下，我们不需要进行编辑，dp[i][j]=dp[i-1][j-1] 第二种情况，a[i]!=b[j]，如果两个字符不相等，我们有三种处理方式：替换字符串b，编辑距离为dp[i-1][j-1]+1；插入一个字符与其相等，则编辑距离为dp[i-1][j]+1；删除该字符，编辑距离为dp[i][j-1]+1，三者取其小即可。具体以下图为例

三、代码参考


import java.util.Scanner;

public class Main {
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        while(sc.hasNext()){
            String a = sc.nextLine();
            String b = sc.nextLine();
            int[][] dp = new int[a.length()+1][b.length()+1];  //定义动规数组

            for(int i=1; i<=a.length(); i++){  // 初始化
                dp[i][0] = i;
            }
            for(int i=1; i<=b.length(); i++){  // 初始化
                dp[0][i] = i;
            }
            for(int i=1; i<=a.length(); i++){
                for(int j=1; j<=b.length(); j++){
                    if(a.charAt(i-1)==b.charAt(j-1)){  //第一种情况
                        dp[i][j] = dp[i-1][j-1];
                    }else{  //第二种情况
                        dp[i][j] = Math.min(dp[i-1][j]+1, Math.min(dp[i-1][j-1]+1, dp[i][j-1]+1));  //状态转移方程
                    }
                }
            }
            System.out.println(dp[a.length()][b.length()]);
        }
    }
}


--------------------------------------------------------


"""
dp[i][j]
i-1 为 str2 第 i 个字符
j-1 为 str1 第 j 个字符

例如：
str1 = abc
str2 = abcde
假设始终对str1进行操作
输出为dp[5][3]

添加：
str1 = abc+e
str2 = abcde
即dp[5][3] = dp[4][3] + 1
即dp[i][j] = dp[i-1][j] + 1

删除：
str1 = abc-c
str2 = abcde
即dp[5][3] = dp[5][4] + 1
即dp[i][j] = dp[i][j-1] + 1

替换：
str1 = abc → abe
str2 = abcde
同时去掉e，转换为
str1 = ab
str2 = abcd
即dp[5][3] = dp[4][2] + 1
即dp[i][j] = dp[i-1][j-1] + 1
"""
while True:
    try:
        str1 = input()
        str2 = input()
        m = len(str1)
        n = len(str2)
        dp = [[1] * (m + 1) for i in range(n + 1)]
        for i in range(m + 1):
            dp[0][i] = i
        for j in range(n + 1):
            dp[j][0] = j
        for i in range(1, n + 1):  # i-1为str2第i个字符
            for j in range(1, m + 1):  # j-1为str1第j个字符
                if str1[j - 1] == str2[i - 1]:
                    dp[i][j] = dp[i - 1][j - 1]
                else:
                    a_d_d = dp[i - 1][j] + 1
                    d_e_l = dp[i][j - 1] + 1
                    re_pl_ace = dp[i - 1][j - 1] + 1
                    dp[i][j] = min(a_d_d, d_e_l, re_pl_ace)
        print(dp[n][m])
    except:
        break





--------------------------------------------------------------


#include <stdio.h>
#include <string.h>

int mix(int a,int b,int c){
    a=(a<b)?a:b;
    a=(a<c)?a:c;
    return a;
}

void d_p(char *str0,char *str1){
    int i,j,len0,len1;
    len0=strlen(str0);
    len1=strlen(str1);
    int dp[len0+1][len1+1];
    dp[0][0]=0;
    for(i=1;i<len0+1;i++) dp[i][0]=i;
    for(i=1;i<len1+1;i++) dp[0][i]=i;
    for(i=1;i<len0+1;i++){
        for(j=1;j<len1+1;j++){
            if(str0[i-1]==str1[j-1]) dp[i][j]=dp[i-1][j-1];
            else dp[i][j]=mix(dp[i-1][j-1]+1,dp[i][j-1]+1,dp[i-1][j]+1);
        }
    }

    printf("%d \n",dp[len0][len1]);
}

int main(void) { 
	char str0[1000],str1[1000];

	while(scanf("%s",str0)!=-1){
	    scanf("%s",str1);
	    d_p(str0,str1);
	}
	return 0;
}