最大子串和

题目描述

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。
子数组 是数组中的一个连续部分。

样例

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

提示

• $1<=nums.length<=105$
• $-104<=nums[i]<=104$
• https://leetcode-cn.com/problems/maximum-subarray

分析

• 原问题：找出一个具有最大和的连续子数组

• 子问题：求前 i 项的最大连续子数组的最大和

• DP 定义：表示前 i 项的最大连续子数组的最大和（第 i 项必选）

• DP 方程：$dp[i]=max(dp[i-1]+nums[i],nums[i])$

  若 $dp[i-1]>0$，则 $dp[i]=dp[i-1]+nums[i]$ ，否则 $dp[i]=nums[i]$

• DP 初始化：无

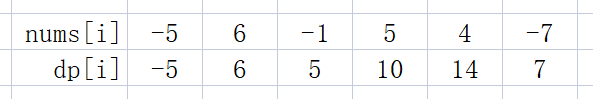
代码

class Solution {
    public int maxSubArray(int[] nums) {
        int[] dp = new int[nums.length];
        int max = nums[0];
        dp[0] = nums[0];
        for(int i = 1; i < nums.length; i++) {
            dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);
            max = Math.max(max, dp[i]);
        }
        return max;
    }
}