引言

笔者一直觉得在计算机这一学科的学习中，离散数学是极为重要的知识基础。离散化的思想体现在计算机学科的方方面面。举例来说，“像素”这一概念是我们日常生活中耳熟能详的，将一个图片拆分成一个个极微小的像素，就是利用了离散化的思想。为了帮助大家打好离散数学的思维基础，笔者新开一个专栏，对《离散数学导学》这本书做一个精炼，使其更易理解。这篇文章是这个专栏的第四部分，主要介绍第8章。
1-3章传送门
4-5章传送门
6-7章传送门

正文

首先明确一点，关系是特殊的集合，函数是特殊的关系。

第八章关系

定义

关系是笛卡尔积的一个子集，也就是序偶的集合。

“(a，b)满足关系R”可以写成(a，b)∈R，R(a，b)，a→b。当写成最后一种形式时，将（a，b）看作关系中的一种映射。

我们这里举个书上的例子：
在这里插入图片描述
A↔B是P(A×B)，也就是A×B的幂集。在这里A和B分别是两个集合。

定义域，值域

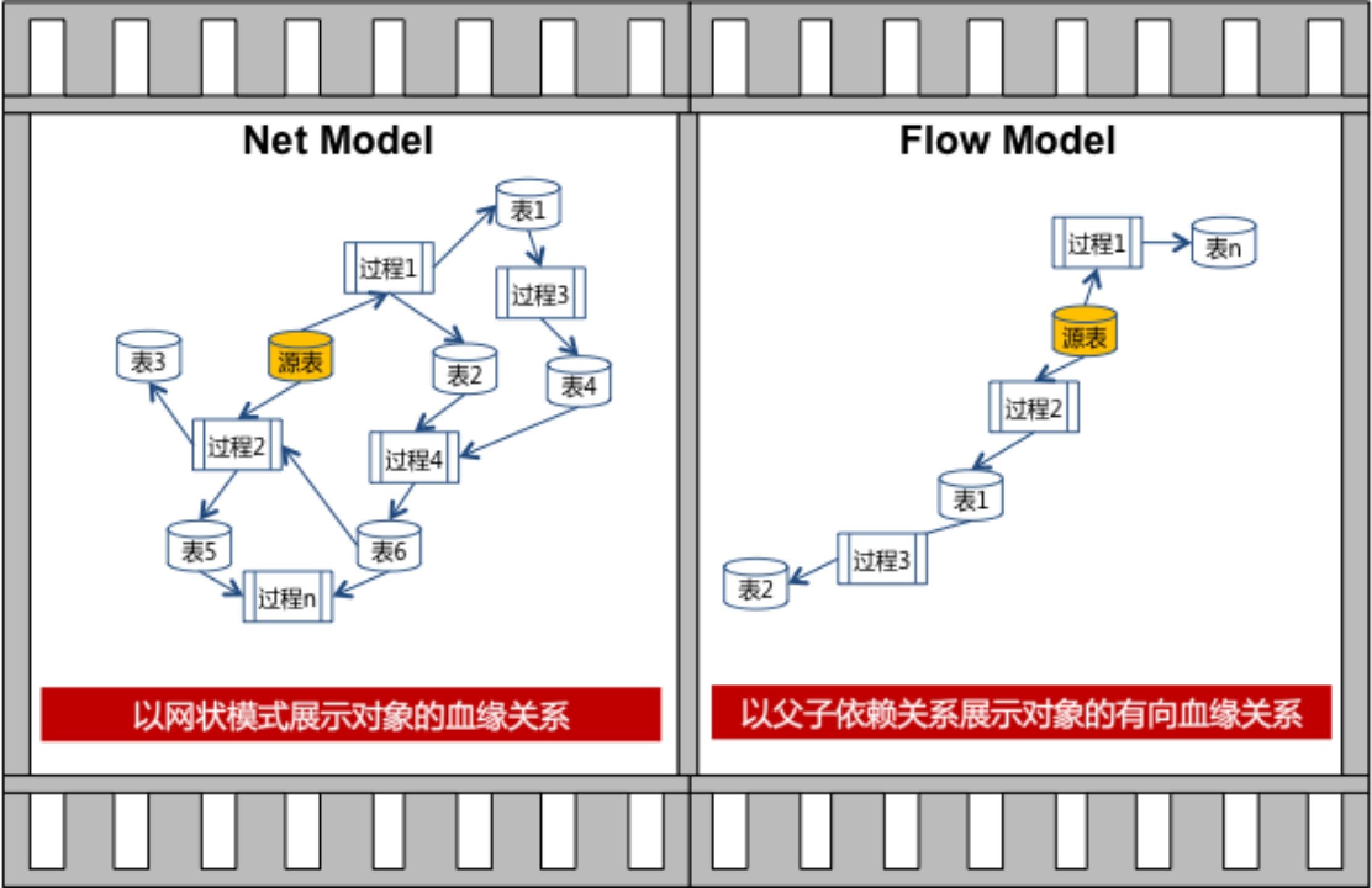
我们知道，关系是笛卡尔积的子集，如果这个笛卡尔积是A×B，那么我们定义A是关系的源头，B是关系的目标。定义域指A中出现在关系中的所有元素的集合，值域指B中出现在关系中的所有元素的集合。我们举个例子：
在这里插入图片描述
注意下面的土豆图，这个图可以很形象的表示一个关系。从图中我们可以看出， House_mate集合是这个关系的源头及目标，但它的定义域是{凯琳，马特}，值域是{凯莉，马特}。关系R的定义域符号是dom R，值域符号是ran R。

关系的逆

一个关系的逆就是把关系的源头和目标反过来，比如上述的关系的逆就是{(马特→凯琳)，(凯莉→马特)}。关系R的逆称作R^~或R^-1。

关系上的运算（重点）

定义域限制符◅，它产生一个新的关系，这个关系的定义域是原关系的定义域与定义域限制符左边的集合的交集。举例：

原关系为{a→1，b→2，c→3}，则{a}◅{a→1，b→2，c→3}={a→1}。

注意，定义域限制符左右都是集合。

定义域伴随限制符
定义域伴随限制符可以看作是定义域限制符的补，它返回的关系的定义域是原关系的定义域减定义域限制符左边的集合的差运算。定义域限制符的符号是定义域限制符中间画一条横线（原谅笔者实在没找到这个符号）。
值域限制符▻：和定义域限制符相似。
值域伴随限制符⌲：和定义域伴随限制符相似。定义域伴随限制符的符号就是它的反向。
关系的像：给定关系R，它的像运算符是R(|A|)，其中A是个集合。这个运算返回一个值域的子集。举例：

R是{a→1，b→2，c→3}，则R(|{a，b}|)={1，2}。

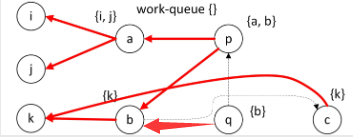
关系的合成

给定两个关系A和B，我们称A○B是这两个关系的合成关系。我们用土豆图来说明这个：

这是关系A的土豆图：
这是关系B的土豆图：
合成运算就是将B接到A的后面，形成这样一个土豆图：
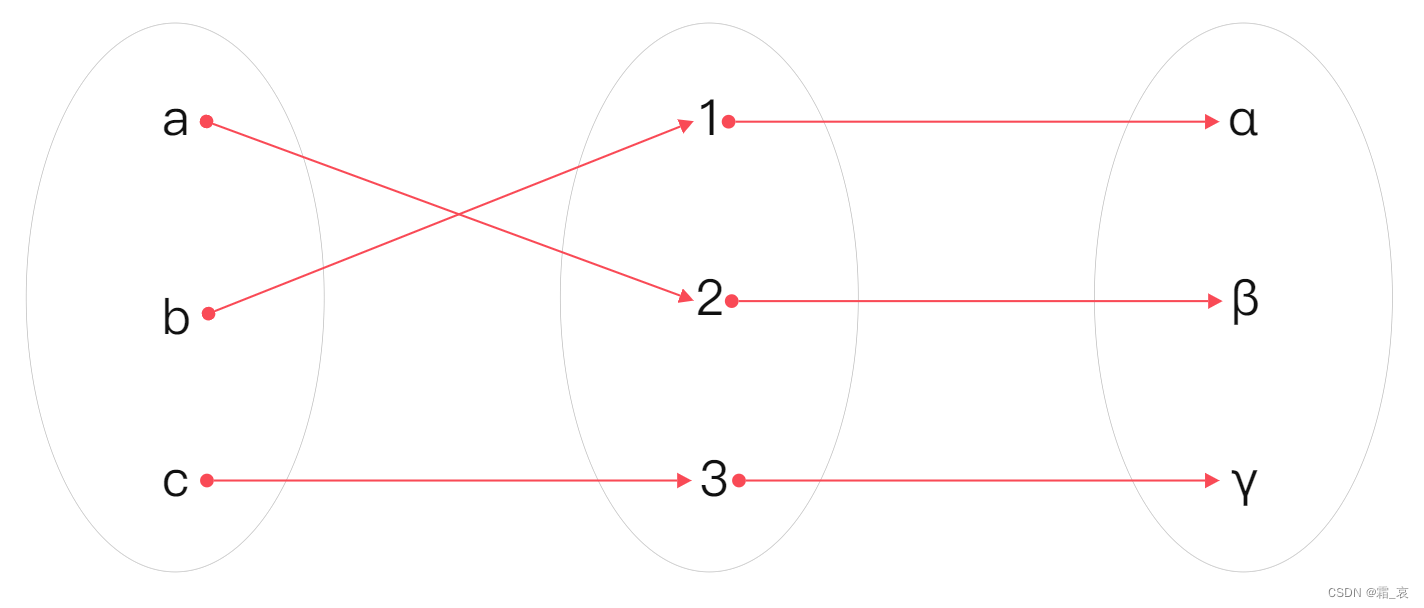
观察这个图，a映射到2，2映射到β，因此a可以直接映射到β，其他元素也同理。因此就得出了合成后的关系：

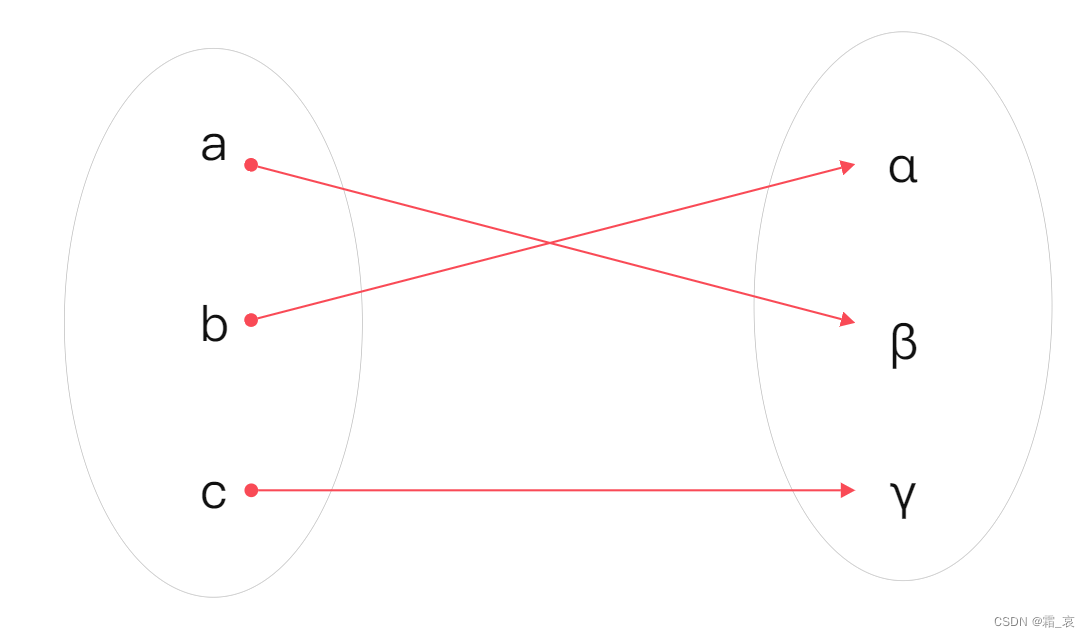
这就是关系的合成。注意：从合成过程中我们可以看出，关系合成必须要求B的源头集合和A的目标集合是一个类型的，否则合成计算是未定义的。

同类关系和异类关系

一个关系的源头和目标集合如果是同一类型的，就称之为同类关系；反之则称为异类关系。同类关系可以自己与自己进行合成运算，但异类关系不能。

关系的性质（重难点）

关系的性质是个比较难记住的点，没看懂的可以来回看一下。

自反性：在同类关系R中，对于R的源头集合（也可以说是目标集合）X来讲，每一个X中的元素x都满足（x，x）∈R，则R是自反性的
传递性：随意拿出R中的两个序偶（x，y）和（y，z），如果（x，z）也是R中的序偶，那么R是传递性的。如果R是传递性的，那么R○R是R的子集。
对称性：随意拿出R中的一个序偶（x，y），如果（y，x）也是R中的序偶，则R是对称性的
非对称性：随意拿出R中的一个序偶（x，y），要求（y，x）不能是R中的序偶，则R是对称性的
反对称性：反对称性和非对称性其实是完全不同的两个性质。随意拿出R中的一个序偶（x，y），如果存在（y，x），那么y=x。满足这个性质的R是反对称性的。因此，如果R满足非对称性，那么它一定不是反对称性的，因为无法找到两个序偶是（x，y），（y，x）。你可能会觉得反对称性和自反性之间有联系，但经过笔者思考，这两个性质之间其实没有逻辑关系，感兴趣的读者可以自己思考一下。
完全性：在同类关系R中，R的目标集合X中任意挑出任意两个元素，都满足R的映射关系，那么称R是完全的。

顺序与等价（简介）

只有同类关系中定义了以下性质，设这个关系为R，R的源头（目标）是X。

R满足自反、传递、反对称三个性质，则称R是偏序的。此时X中的元素形成某种顺序，某些元素高于其他元素。
R满足反对称、传递、完全三个性质，则称R是全序的。此时X中的所有元素都有某种顺序，因此称为全序。
R满足对称、传递、自反三个性质，则称R是等价的。此时取（x，y）∈R，则x“等价于”y。

闭包

一个同类关系S，加入一些序偶让S满足自反、对称、传递关系，加入后的关系分别被称为S的自反闭包，对称闭包，传递闭包。既满足自反性，又满足传递性的闭包称为自反传递闭包。
构造闭包的方法就是进行并运算，将缺少的序偶以集合的方式加进去。
注意：对于传递闭包来说，传递闭包的定义和传递性不太相同，传递性只需要传递一次，但传递闭包需要传递n次，即它不仅要补上S○S（可以写成S²)，也要补上S○S○S(S³)，一直到n次合成后合成的关系是空集为止。