注:本文主要介绍六大排序中的快排
文章目录
- 前言
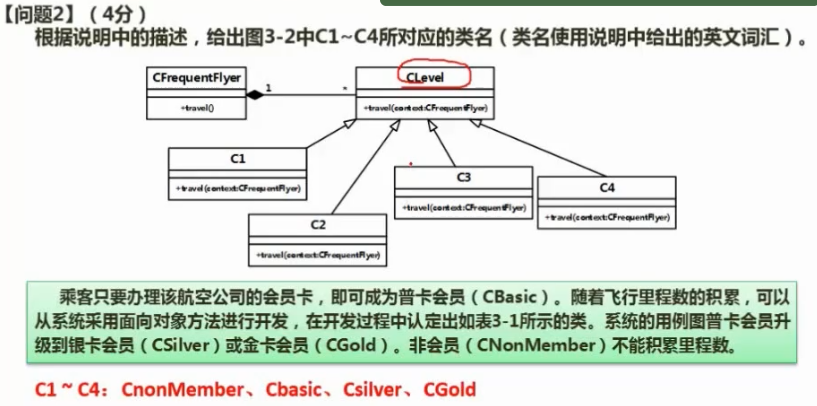
- 一、三大法则
- 1.1 Hoare法
- 1.2 挖坑法
- 1.3 双指针法(更加便捷)
- 1.4 三种方法时间复杂度计算
- 二、快排栈问题优化方式
- 2.1 三数取中
- 2.2 小区间优化
- 三、非递归快排
前言
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
一、三大法则
1.1 Hoare法
什么是Hoare法则呢?
Hoare法是指在对数组进行排序时,定义两个变量,与一个在单子循环中不变的key值,右值先动找比key小的数字,找到后左值动,找比key大的数字,后进行交换以完成对数组的排序。
初始状态
right先进行寻找,找到5<key3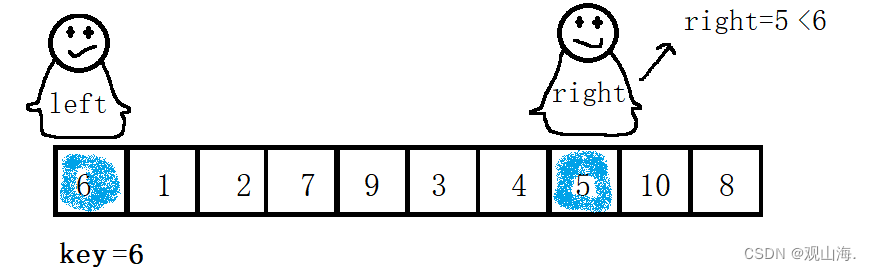
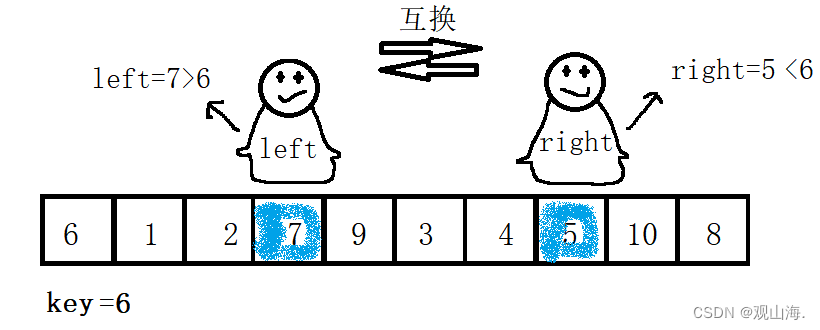
left进行寻找找到7>key,进行交换
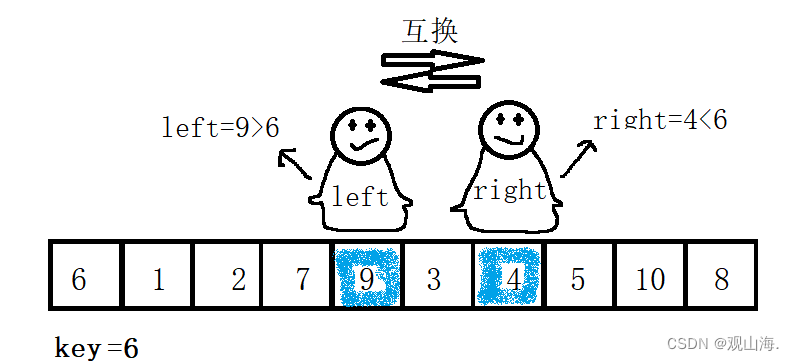
继续进行刚才的工作交换9/4
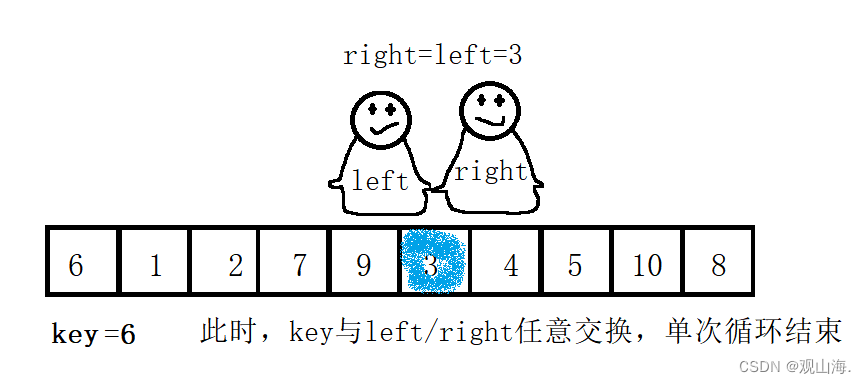
当左值与右值相等时,一次循环结束,left与right所在位置与初始的key位置进行Swap交换,进入递归循环。
1.Hoare法代码
void PartSort1(vector<int>& v, int begin, int end)
{
//出递归判断
if (begin >= end)
{
return;
}
int key = begin;
int left = begin, right = end;
while (left < right)
{
//寻找小于key的左值
while (right > left && v[right] >= v[key])
{
right--;
}
//寻找大于key的右值
while (right > left && v[left] <= v[key])
{
left++;
}
Swap(v[left], v[right]);
}
Swap(v[key], v[left]);
//key左边都是小于key的数,key右边都是大于key的数字
key = left;
//进入递归,先递归左半部分小于key的区间,后递归右半部分大于key的区间
QuickSort(v, begin, key - 1);
QuickSort(v, key + 1, end);
}
int main()
{
vector<int> v = { 8,12,5,3,6,4,7,91,5,16,35,21,52,2,1 };
QuickSort(v, 0, v.size() - 1);
PrintArray(v, v.size());
return 0;
}
排序结果

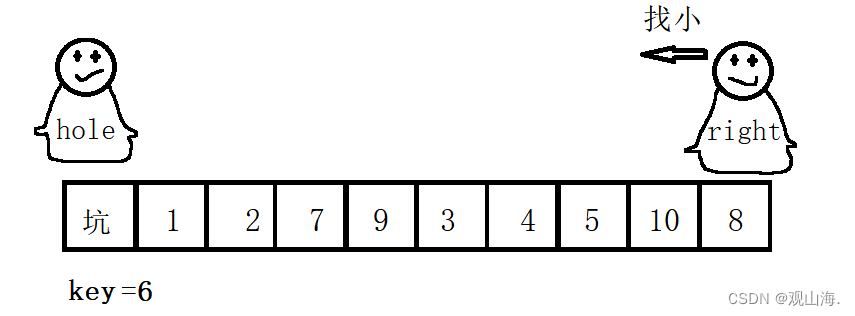
1.2 挖坑法
挖坑法原理与Hoare法一致,不过相较于Hoare法更易理解它遵循着两个原则
1.先将第一个数据存放在临时变量key中。
2.左边是坑的话,右边先走找小,找到后与左坑值交换,右位变成坑位。
3.左边再找大值,交换循环。
初始状态

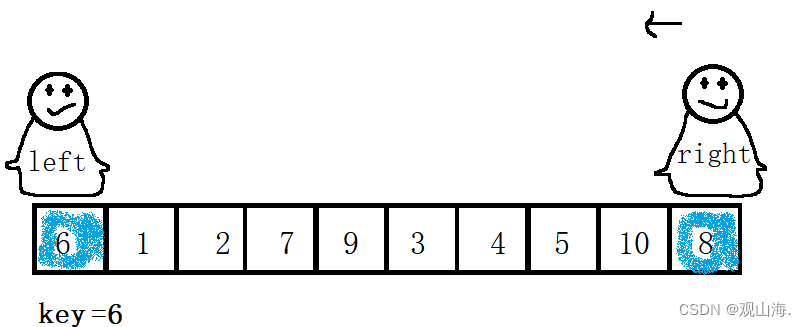
right找到第一个小于key的值5,然后将5给与坑所在位置,将right位置为坑
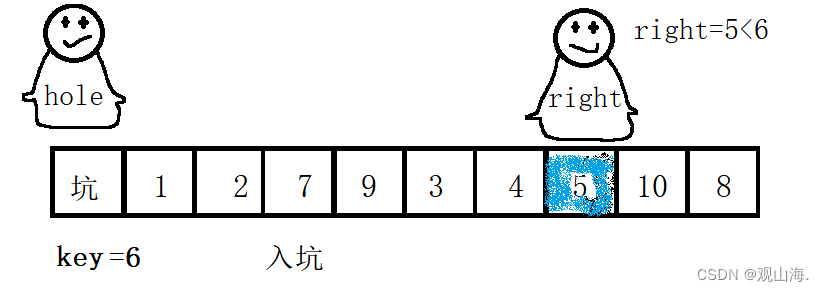
left开始找大
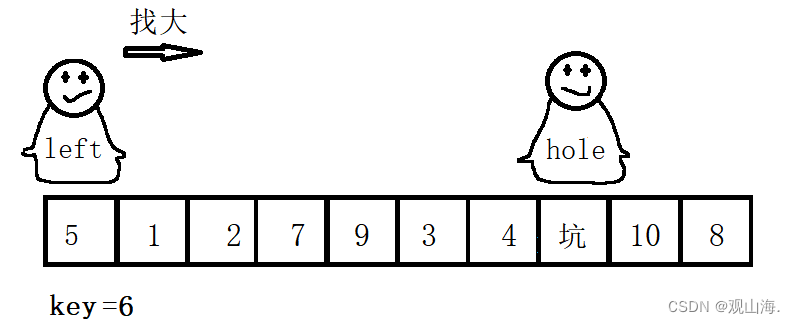
left找到第一个大于key的数7,与坑置换,并将left位置设为坑
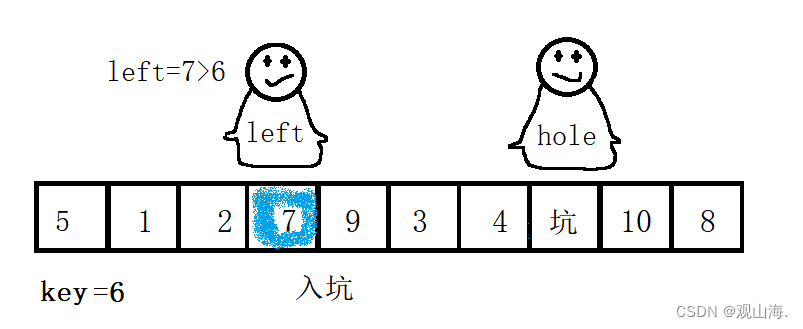
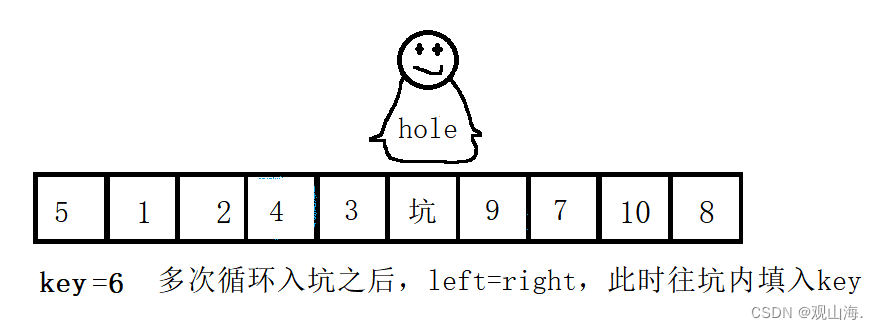
多次置换后left==right时,坑的左边都是小于key的数,坑的右边都是大于key1的数,将key赋值于坑所在位置,单词排序成功,进入递归
2.挖坑法代码
void QuickSort(vector<int>& v, int begin, int end)
{
if (begin >= end)
{
return;
}
int left = begin, right = end;
int key = v[left], hole = left;
while (left < right)
{
//找右值
while (left < right && v[right] >= key)
{
--right;
}
//入坑,与坑的替换
v[hole] = v[right];
hole=right;
while (left < right && v[left] <= key)
{
++left;
}
v[hole] = key;
hole = left;
}
v[hole] = key;
//进入递归,先递归左半部分小于key的区间,后递归右半部分大于key的区间
QuickSort(v, begin, hole - 1);
QuickSort(v, hole + 1, end);
}
int main()
{
vector<int> v = { 8,12,5,3,6,4,7,91,5,16,35,21,52,2,1 };
QuickSort(v, 0, v.size() - 1);
PrintArray(v, v.size());
return 0;
}
排序结果与Hoare相同
1.3 双指针法(更加便捷)
1.cur找比key小的,找到后停下。
2.prev++,prev与cur所在交换。
初始状态,这边我定义cur从第二个位置开始,当然它也可以从第一个位置开始,具体可以在程序中改进
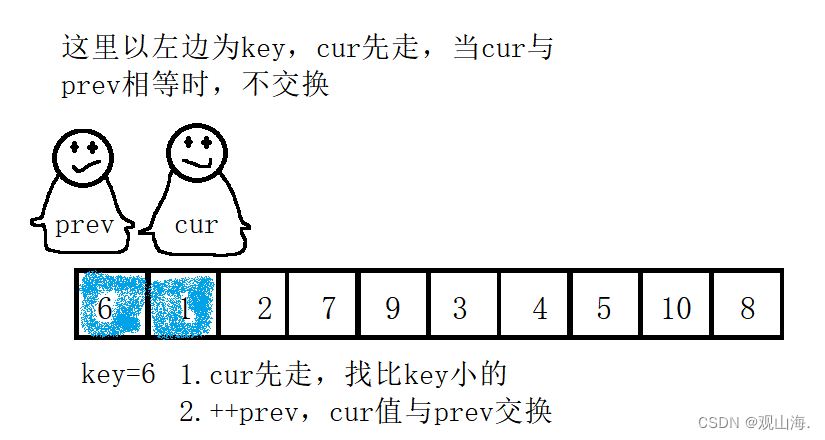
当prev与cur相同时不进行交换,继续便利寻找可交换的数字找到第一组7/3,进行交换
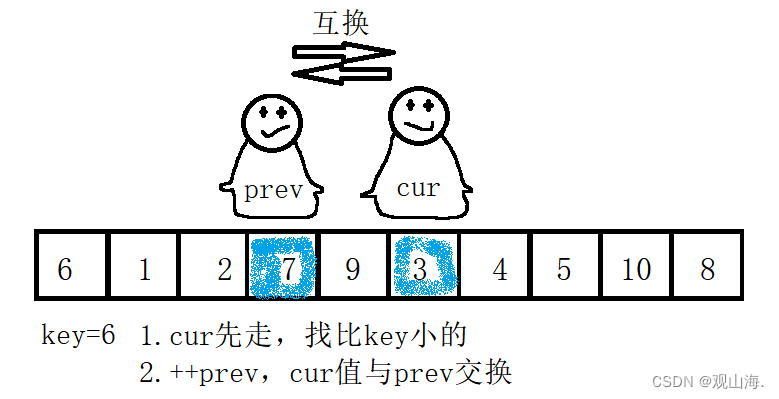
找到第二组交换数据9/4,进行交换
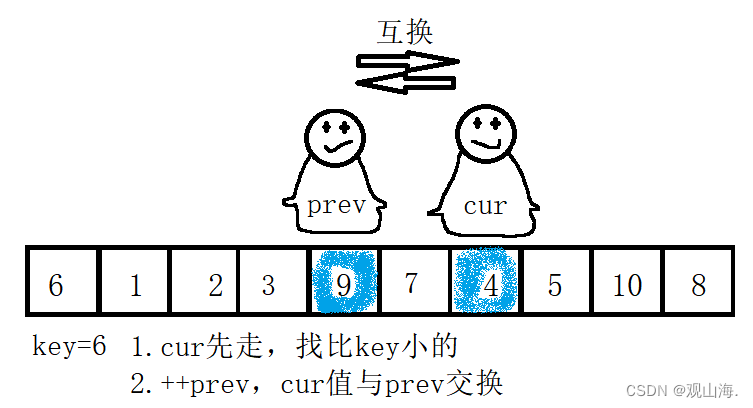
多次交换后我们可以发现cur走到了最后的位置,此时,一次循环结束,当然不要忘记将初始设置的key与最后prev位置的数字进行交换。我们就可以得到以prev为分界线的左边小,右边大的两个数据区间,进行递归排序
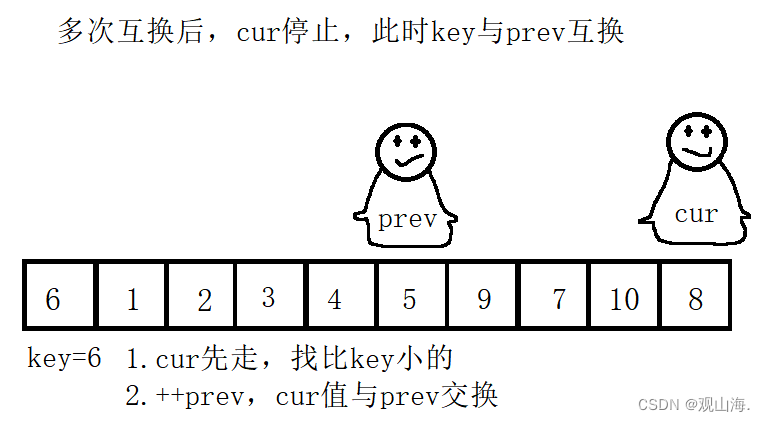
结果
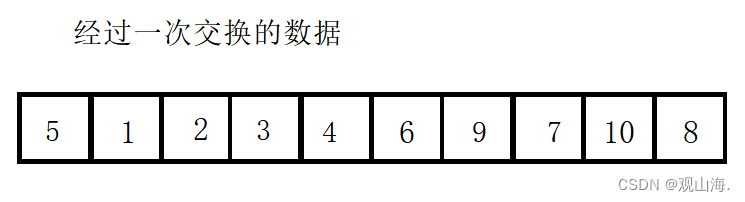
3.双指针法代码
void QuickSort(vector<int>& v, int begin, int end)
{
if (begin > end)
{
return;
}
int prev = begin, cur = begin+1;
int key = begin;
while (cur <= end)
{
//当prev与cur相等时交换的写法
/*if (v[cur] < v[key])
{
prev++;
Swap(v[prev], v[cur]);
}*/
//当prev与cur相等时直接跳过不交换的写法
if (v[cur] < v[key] && ++prev != cur)
{
Swap(v[prev], v[cur]);
}
cur++;
}
Swap(v[prev], v[key]);
key = prev;
QuickSort(v, begin, key - 1);
QuickSort(v, key + 1, end);
}
int main()
{
vector<int> v = { 8,12,5,3,6,4,7,91,5,16,35,21,52,2,1 };
QuickSort(v, 0, v.size() - 1);
PrintArray(v, v.size());
return 0;
}
1.4 三种方法时间复杂度计算
这里较难描述,我直接给出答案以及答案出现的情乱
快排的时间复杂度最理想下可达到O(n*logn)。
当一组数据趋近于有序(逆序、正序)时,时间复杂度可达O(n * n)。
这是为什么呢?
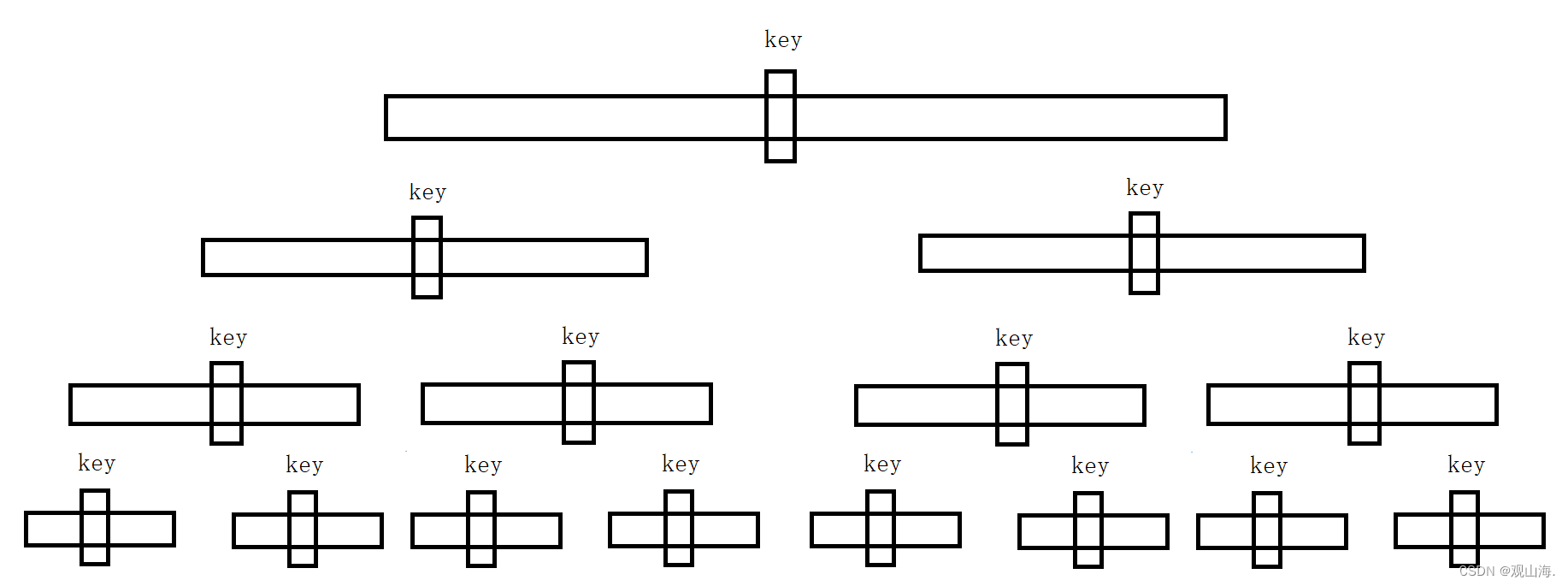
话不多说直接上图
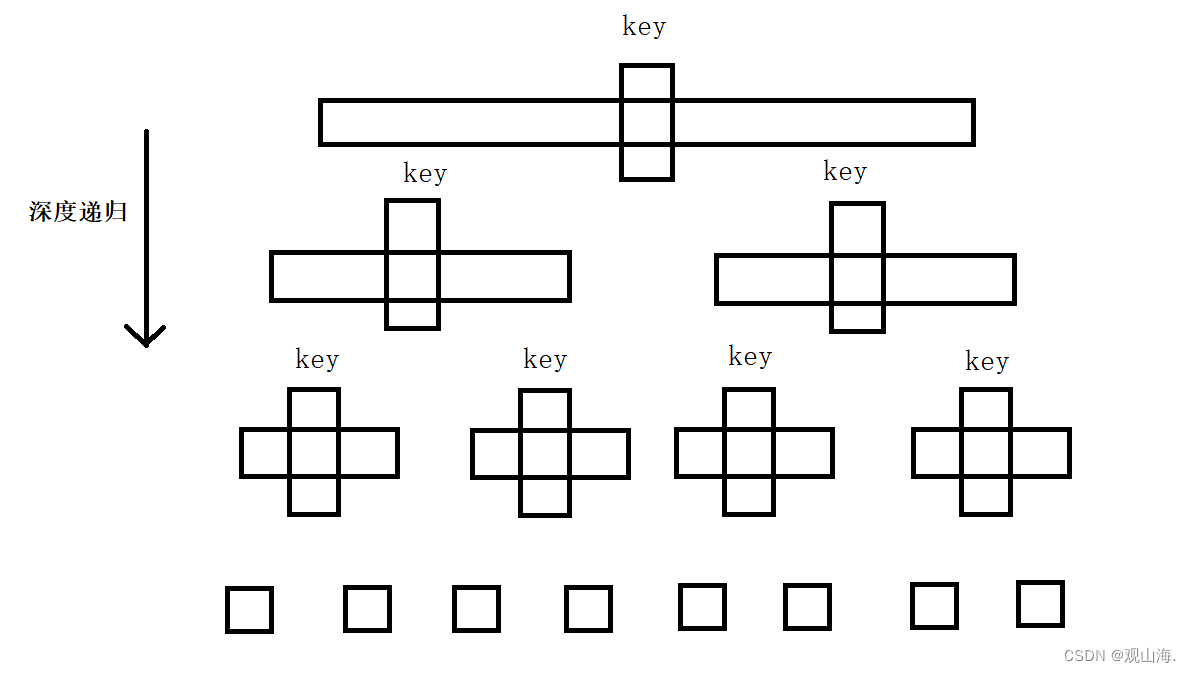
这张图是不是和二叉树很像,当每次key都能选到,中间值时,它的时间复杂度就是n*logn。
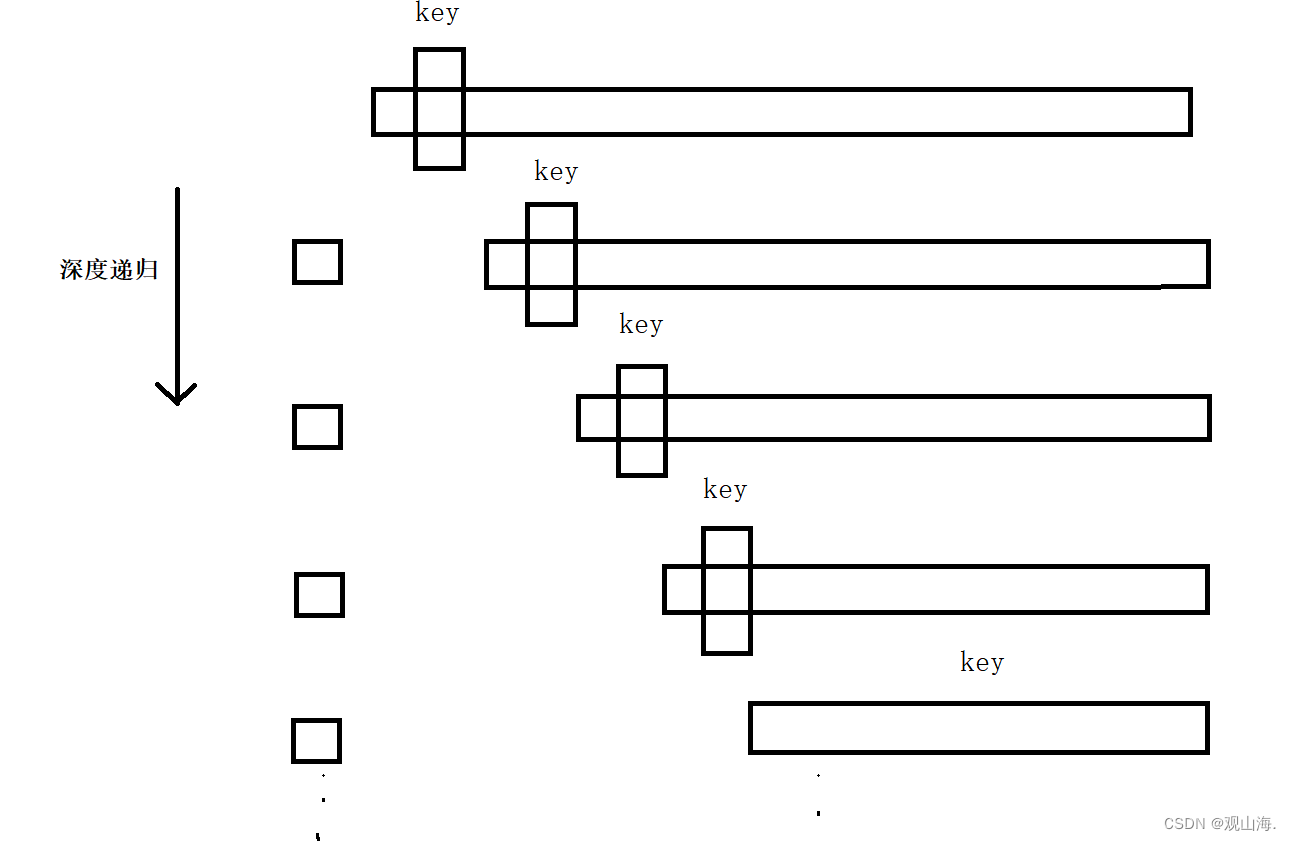
而当所排数组趋近于有序数组时,就会出现如上图所示的情况,而我们又知道,进行递归时,CPU需要不停的进行栈帧的开辟,如果遇到趋近于有序的数组时,时间复杂度为O(n * n),我们得不到想要的有序数组,还会使编译器崩溃,那它怎么能叫快排的,徒有其表吗。
接下来要讲两种规避这种情况的优化方式。
1.三数取中
2.小区间优化
二、快排栈问题优化方式
2.1 三数取中
三数取中法选key,可以解决上述最坏情况有序(顺序、逆序)的问题。
有效避免因为深度遍历而开过多栈,引起的栈溢出问题。
思维图:
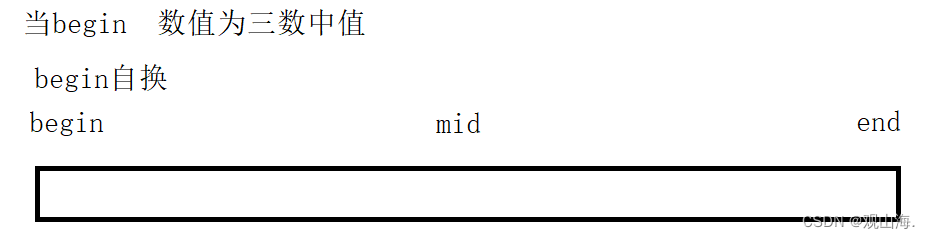
初始状态
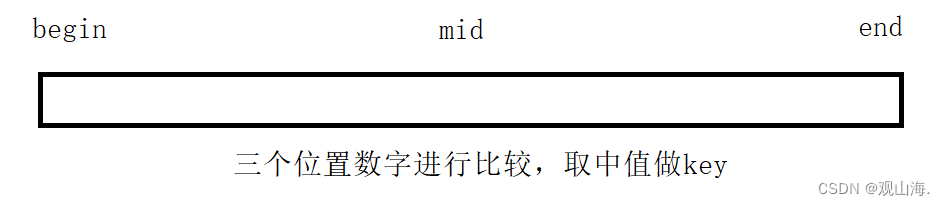
mid为中值

end为中值
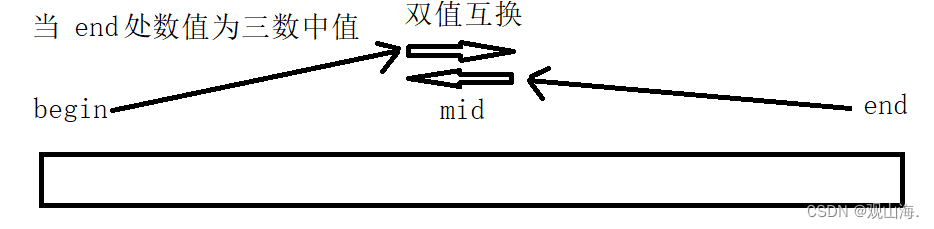
begin为中值
//中值判断函数
int GetMidIndex(vector<int>& v, int begin, int end)
{
int mid = (begin + end) / 2;
if (v[begin] < v[mid])
{
if (v[mid] < v[end])
{
return mid;
}
else if (v[begin] > v[end])
{
return begin;
}
else
{
return end;
}
}
else // v[begin] > v[mid]
{
if (v[mid] > v[end])
{
return mid;
}
else if (v[begin] < v[end])
{
return begin;
}
else
{
return end;
}
}
}
//加入中止判断的快排
void QuickSort(vector<int>& v, int begin, int end)
{
if (begin > end)
{
return;
}
//加入中值判断
int mid = GetMidIndex(v, begin, end);
Swap(v[begin], v[mid]);
int prev = begin, cur = begin+1;
int key = begin;
while (cur <= end)
{
/*if (v[cur] < v[key])
{
prev++;
Swap(v[prev], v[cur]);
}*/
if (v[cur] < v[key] && ++prev != cur)
{
Swap(v[prev], v[cur]);
}
cur++;
}
Swap(v[prev], v[key]);
key = prev;
QuickSort(v, begin, key - 1);
QuickSort(v, key + 1, end);
}
2.2 小区间优化
小区间优化,字如其名,在进行递归排序时,会无限制的进行栈帧开辟,但是我们所用的内存空间的栈区往往最大就只有8M大小的空间,有概率会爆栈。
经过多次排序后的数据在每个小区间会十分集中。
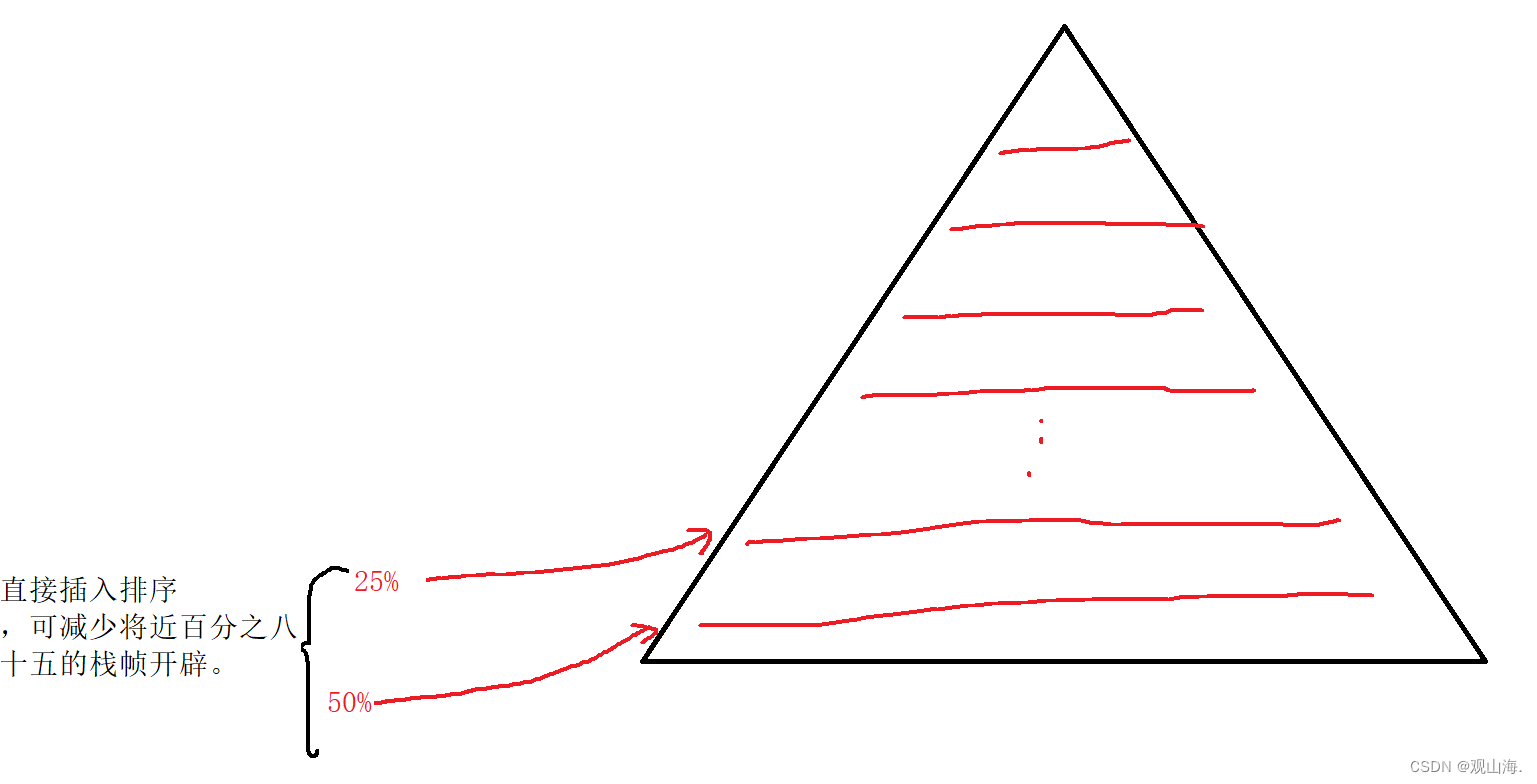
此时进行小区间的优化可以避免少开70%~90%的栈帧。
方法: 当小区间元素小于10/15时,使用直接插入排序进行排序。
思维图:
在所排数组非常大的情况下,如下图,会无线的开辟栈帧
适当的裁剪,换取更高的效率,减少百分之八十五左右的栈帧开辟
//直接插入排序
void InsertSort(vector<int>& v, int n)
{
for (int i = 0; i < n - 1; ++i)
{
int end = i;
int tmp = v[end + 1];
while (end >= 0)
{
if (tmp < v[end])
{
v[end + 1] = v[end];
--end;
}
else
{
break;
}
}
v[end + 1] = tmp;
}
}
//加入三数取中与小区间优化的快排
void QuickSort(vector<int>& v, int begin, int end)
{
if (begin >= end)
{
return;
}
//小区间优化,防止递归深度过大,进行的剪枝行为,后使用直接插入排序进行小范围排序
if (end - begin + 1 < 10)
{
InsertSort(v, end);
}
else
{
//三数取中
int mid = GetMidIndex(v, begin, end);
Swap(v[begin], v[mid]);
int prev = begin, cur = begin + 1;
int key = begin;
while (cur <= end)
{
/*if (v[cur] < v[key])
{
prev++;
Swap(v[prev], v[cur]);
}*/
if (v[cur] < v[key] && ++prev != cur)
{
Swap(v[prev], v[cur]);
}
cur++;
}
Swap(v[prev], v[key]);
key = prev;
QuickSort(v, begin, key - 1);
QuickSort(v, key + 1, end);
}
}
递归类快排,整体代码
#include <iostream>
#include <stack>
#include <vector>
using namespace std;
//交换
void Swap(int& a, int& b)
{
int tmp = a;
a = b;
b = tmp;
}
//打印
void PrintArray(vector<int> v,int n)
{
for (int i = 0; i < n; ++i)
{
cout << v[i] << " ";
}
printf("\n");
}
//三数取中
int GetMidIndex(vector<int>& v, int begin, int end)
{
int mid = (begin + end) / 2;
if (v[begin] < v[mid])
{
if (v[mid] < v[end])
{
return mid;
}
else if (v[begin] > v[end])
{
return begin;
}
else
{
return end;
}
}
else // v[begin] > v[mid]
{
if (v[mid] > v[end])
{
return mid;
}
else if (v[begin] < v[end])
{
return begin;
}
else
{
return end;
}
}
}
//直接插入排序 O(n*n)
void InsertSort(vector<int>& v, int n)
{
for (int i = 0; i < n - 1; ++i)
{
int end = i;
int tmp = v[end + 1];
while (end >= 0)
{
if (tmp < v[end])
{
v[end + 1] = v[end];
--end;
}
else
{
break;
}
}
v[end + 1] = tmp;
}
}
//一、Hoare法
void QuickSort(vector<int>& v, int begin, int end)
{
if (begin >= end)
{
return;
}
int key = begin;
int left = begin, right = end;
while (left < right)
{
while (right > left && v[right] >= v[key])
{
right--;
}
while (right > left && v[left] <= v[key])
{
left++;
}
Swap(v[left], v[right]);
}
Swap(v[key], v[left]);
key = left;
QuickSort(v, begin, key - 1);
QuickSort(v, key + 1, end);
}
//二、挖坑法
//先将第一个数据存放在临时变量key中
//左边是坑的话,右边先走找小,找到后与左坑值交换,右位变成坑位
//左边再找大值,交换循环
void QuickSort(vector<int>& v, int begin, int end)
{
if (begin >= end)
{
return;
}
int mid = GetMidIndex(v, begin, end);
Swap(v[begin], v[mid]);
int left = begin, right = end;
int key = v[left];
int hole = left;
while (left < right)
{
while (left < right && v[right] >= key)
{
--right;
}
v[hole] = v[right];
hole=right;
while (left < right && v[left] <= key)
{
++left;
}
v[hole] = v[left];
hole = left;
}
v[hole] = key;
QuickSort(v, begin, hole - 1);
QuickSort(v, hole + 1, end);
}
//三、前后指针法
//1.cur找比key小的,找到后停下
//2.prev++,prev与cur所在交换
void QuickSort(vector<int>& v, int begin, int end)
{
if (begin > end)
{
return;
}
int prev = begin, cur = begin+1;
int key = begin;
while (cur <= end)
{
/*if (v[cur] < v[key])
{
prev++;
Swap(v[prev], v[cur]);
}*/
if (v[cur] < v[key] && ++prev != cur)
{
Swap(v[prev], v[cur]);
}
cur++;
}
Swap(v[prev], v[key]);
key = prev;
QuickSort(v, begin, key - 1);
QuickSort(v, key + 1, end);
}
//三数取中+小区间优化快排
void QuickSort(vector<int>& v, int begin, int end)
{
if (begin >= end)
{
return;
}
//小区间优化,防止递归深度过大,进行的剪枝行为,后使用直接插入排序进行小范围排序
if (end - begin + 1 < 10)
{
InsertSort(v, end);
}
else
{
//三数取中
int mid = GetMidIndex(v, begin, end);
Swap(v[begin], v[mid]);
int prev = begin, cur = begin + 1;
int key = begin;
while (cur <= end)
{
/*if (v[cur] < v[key])
{
prev++;
Swap(v[prev], v[cur]);
}*/
if (v[cur] < v[key] && ++prev != cur)
{
Swap(v[prev], v[cur]);
}
cur++;
}
Swap(v[prev], v[key]);
key = prev;
QuickSort(v, begin, key - 1);
QuickSort(v, key + 1, end);
}
}
int main()
{
vector<int> v = { 8,12,5,3,6,4,7,91,5,16,35,21,52,2,1 };
QuickSort(v, 0, v.size() - 1);
PrintArray(v, v.size());
return 0;
}
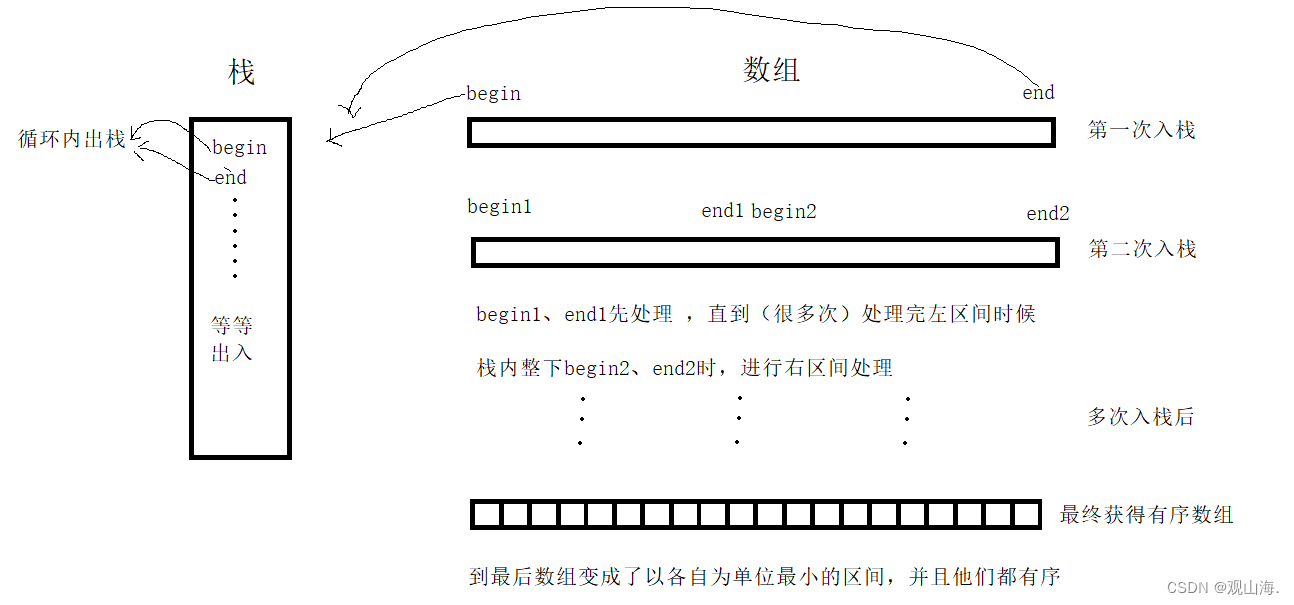
三、非递归快排
非递归快排借助栈进行操作,是一种分治思维的延申。
因为栈的出入规则是先进后出。
我们要对排序区间进行划分,每次的出栈、入栈操作就是递归中处理数据、子区间划分操作。
原理图:
程序:
//非递归快排
void QuickSortNonr(vector<int>& v, int begin, int end)
{
//自定义栈为ST,定义栈st,并初始化栈,将头尾位置压入栈
//成功压入后我们得到需要的排序空间的头和尾
//依次进行出栈入栈,重新定义排序区间,模拟递归排序
ST st;
StackInit(&st);
StackPush(&st, begin);
StackPush(&st, end);
while (!StackEmpty(&st))
{
int right = StackTop(&st);
StackPop(&st);
int left = StackTop(&st);
StackPop(&st);
//调用单次快排,单次排序
int key = QuickSort(a, left, right);
// [left, keyi-1] keyi [keyi+1, right]
if (key + 1 < right)
{
//进行右区间入栈操作,进入模拟递归进入操作
StackPush(&st, key + 1);
StackPush(&st, right);
}
if (left < key - 1)
{
//进行左区间入栈操作,进入模拟递归进入操作
StackPush(&st, left);
StackPush(&st, key - 1);
}
}
//排序完毕销毁
StackDestroy(&st);
}