一、表达式求值

二、隐式类型转换

1.基本概念

2.整型提升的意义

3.详解截断与整型提升的过程

4.char类型范围有关的一些事情

5.有关整形提升的一些案例

三、算术转换

四、操作符的属性

1.优先级表格

2.运算规则

3.一些问题表达式

（1）a*b+c*d+e*f

（1）c+ --c

（3）i=i-- - --i*（i=-3）*i++ + ++i

（4）调用函数时

（5）总结

总结

一、表达式求值

在我们前面介绍了那么多的操作符，我们肯定肯定是需要使用他们的，在使用他们的时候，就会出现各种各样很奇怪的状况。这是因为我们还没有了解一些优先级相关的知识和一些隐式类型转换的问题。所以，我们这部分就来仔细描述一下有关类型转换的那些事。

表达式求值的顺序一部分是由操作符的优先级和结合性来决定的

同样，有些表达式的操作数在求值的过程中可能需要转换为其他类型

二、隐式类型转换

1.基本概念

所谓隐式类型转化，就是偷偷的发生转换，你没有察觉到的一些转换。这种转换，如果不了解，往往会出现一些难以发现的错误。

c的整型算术运算总是以缺省整型类型的精度来进行的（缺省的意思是默认）

为了获得这个精度，表达式中的字符和短整型操作数在使用之前被转换为普通整型，这种转换称为整型提升

我们直接举一个例子

#include<stdio.h>
int main()
{
	char a = 3;
	char b = 127;
	char c = a + b;
	printf("%d", c);
	return 0;
}

由于我们总是以缺省整型类型的精度来进行计算的，所以我们这个char类型的数据在运算的时候会先转化为int类型。然后在进行计算，这就是整型提升

2.整型提升的意义

表达式的整型运算要在CPU的相应运算器件内执行，CPU内整型运算器(ALU)的操作数的字节长度一般就是int的字节长度，同时也是CPU的通用寄存器的长度。

因此，即使两个char类型的相加，在CPU执行时实际上也要先转换为CPU内整型操作数的标准长度。

通用CPU（general-purpose CPU）是难以直接实现两个8比特字节直接相加运算（虽然机器指令中可能有这种字节相加指令）。所以，表达式中各种长度可能小于int长度的整型值，都必须先转换为int或unsigned int，然后才能送入CPU去执行运算

3.详解截断与整型提升的过程

整形提升是按照变量的数据类型的符号位来提升

无符号的整型提升直接补0

我们还是看这段代码

#include<stdio.h>
int main()
{
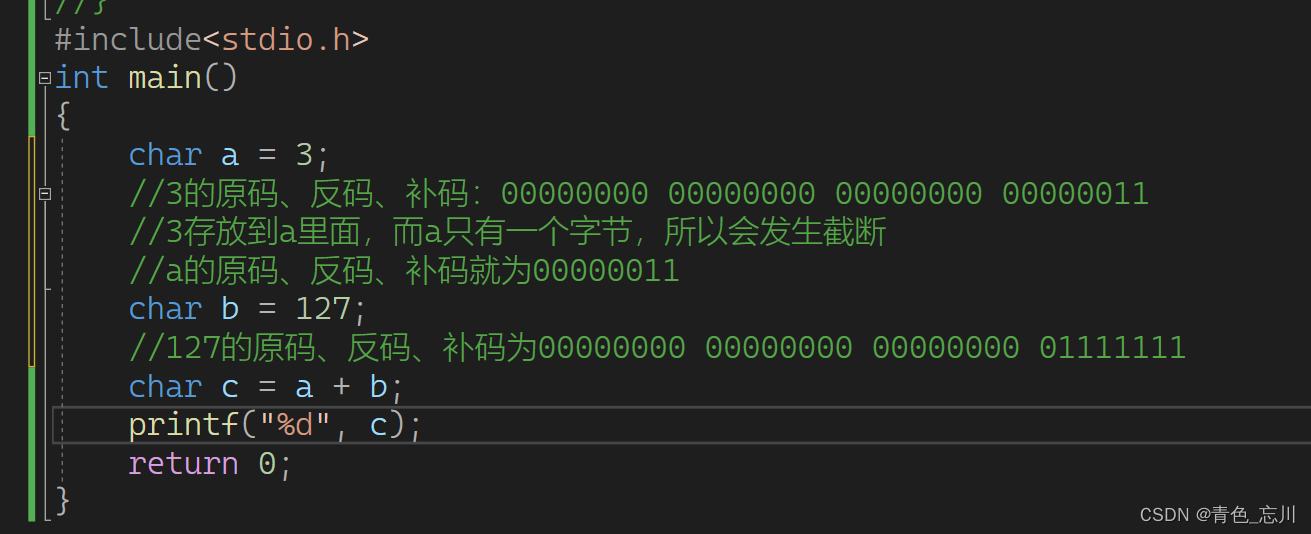
	char a = 3;
	char b = 127;
	char c = a + b;
	printf("%d", c);
	return 0;
}

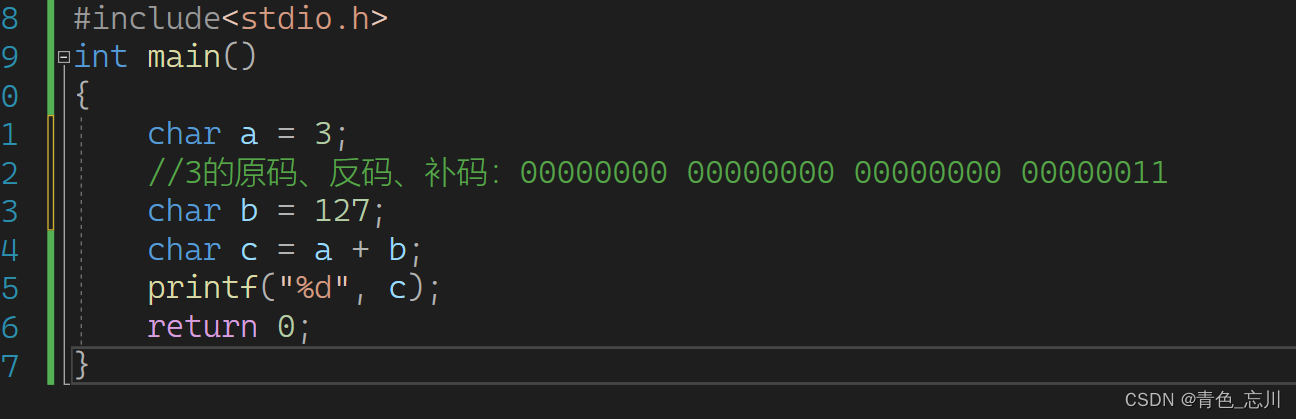
这段代码他一开始是将3赋给a，这里要注意，这个3是一个整数，而整数是四个字节，也就是32个比特位，我们将鼠标放在编译器中的这个3上

我们从这里也能看出来，3是一个整型的。所以我们得先将3的二进制序列写出来

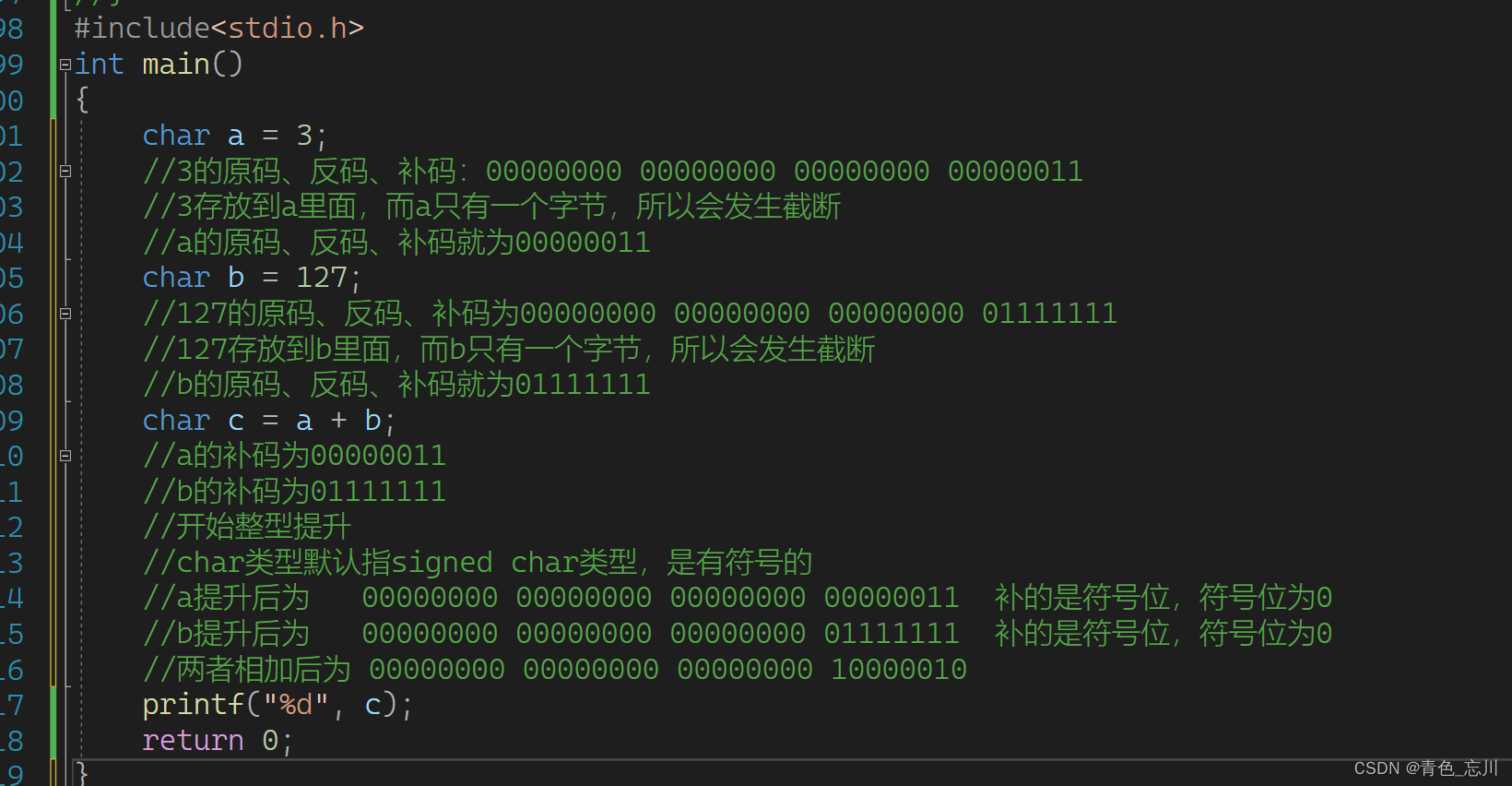
他的原码、反码、补码均为：00000000 00000000 00000000 00000011

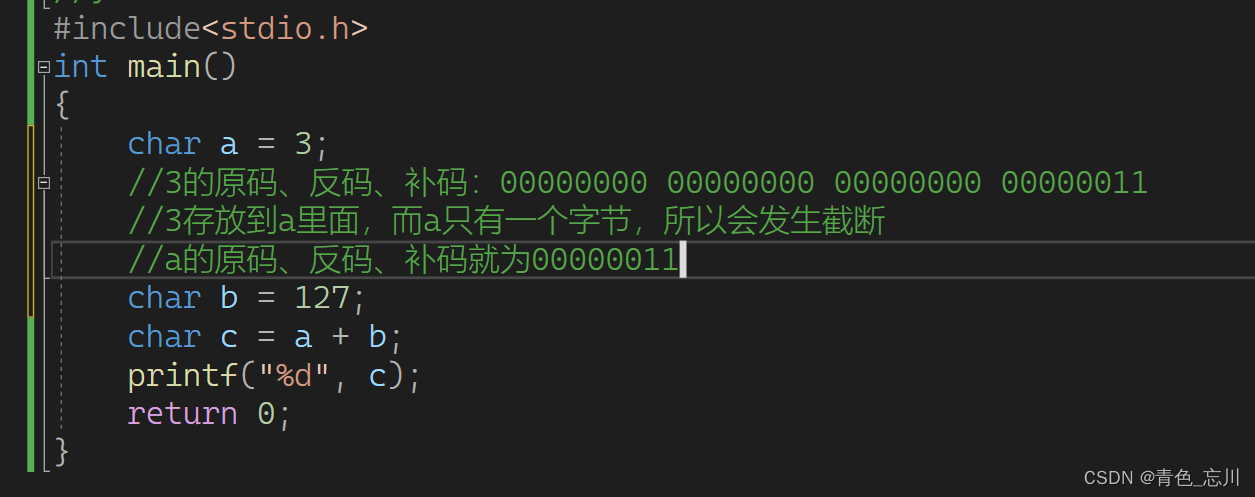
而我们这个3是要存放到a里面去的，a是一个char类型，他只有一个字节，所以会发生截断现象，从右往左数，拿走他需要的比特位，其余的统统砍掉不要了

所以3放到a里面的二进制序列就变为了00000011

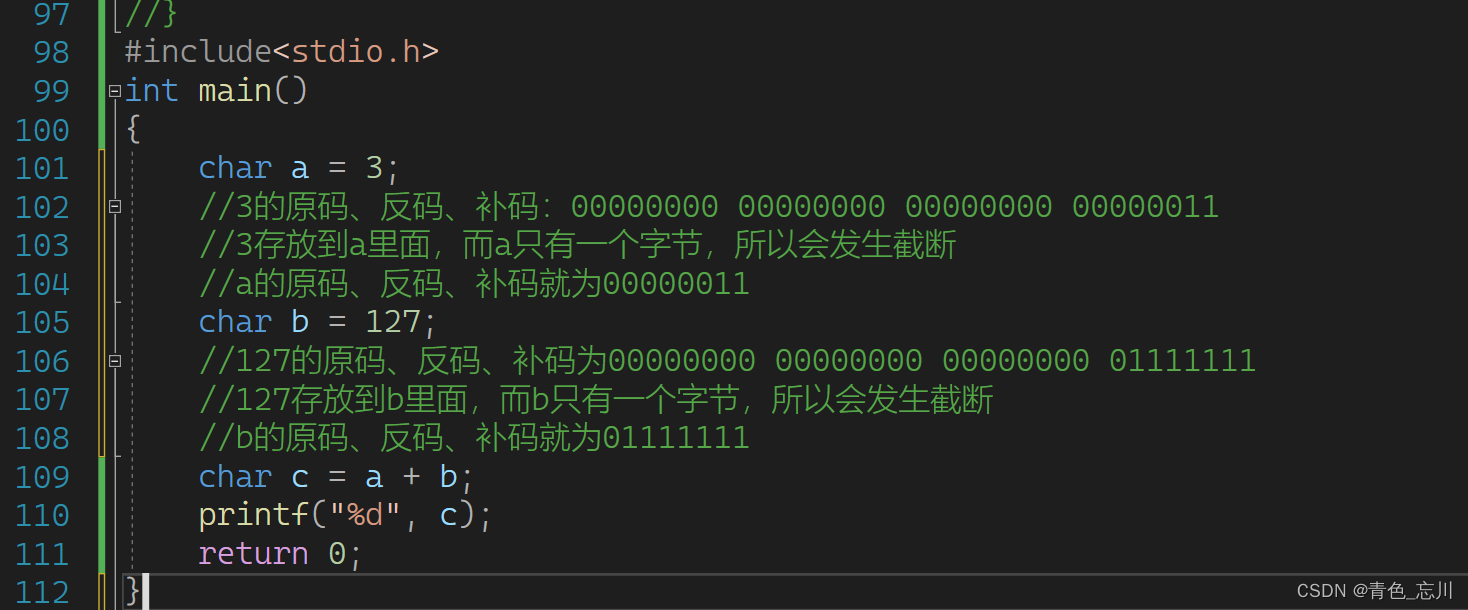
同理b也一样

127的二进制序列为00000000 00000000 00000000 01111111

127放到b里面去，自然要发生截断现象

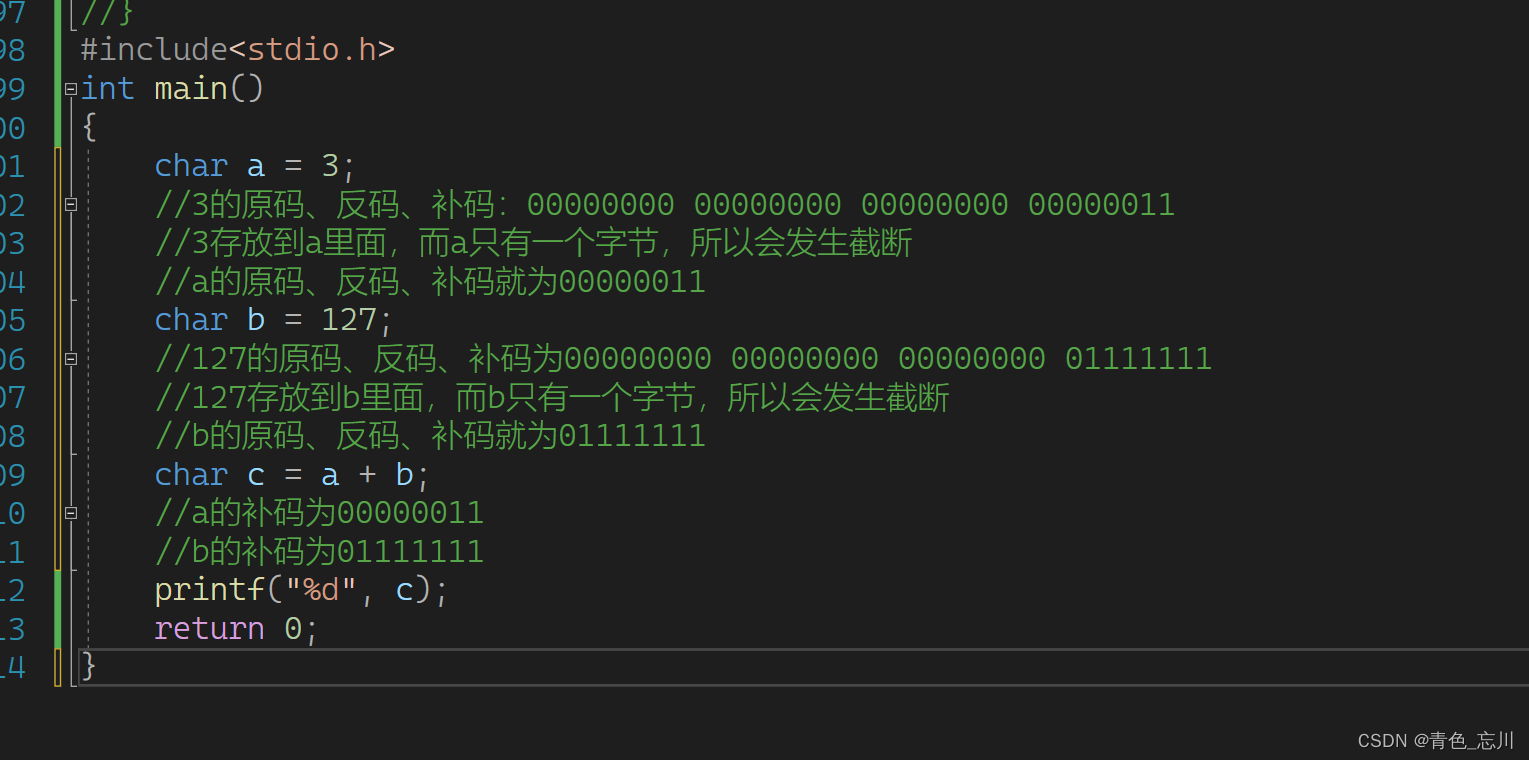
所以此时a与b要进行相加

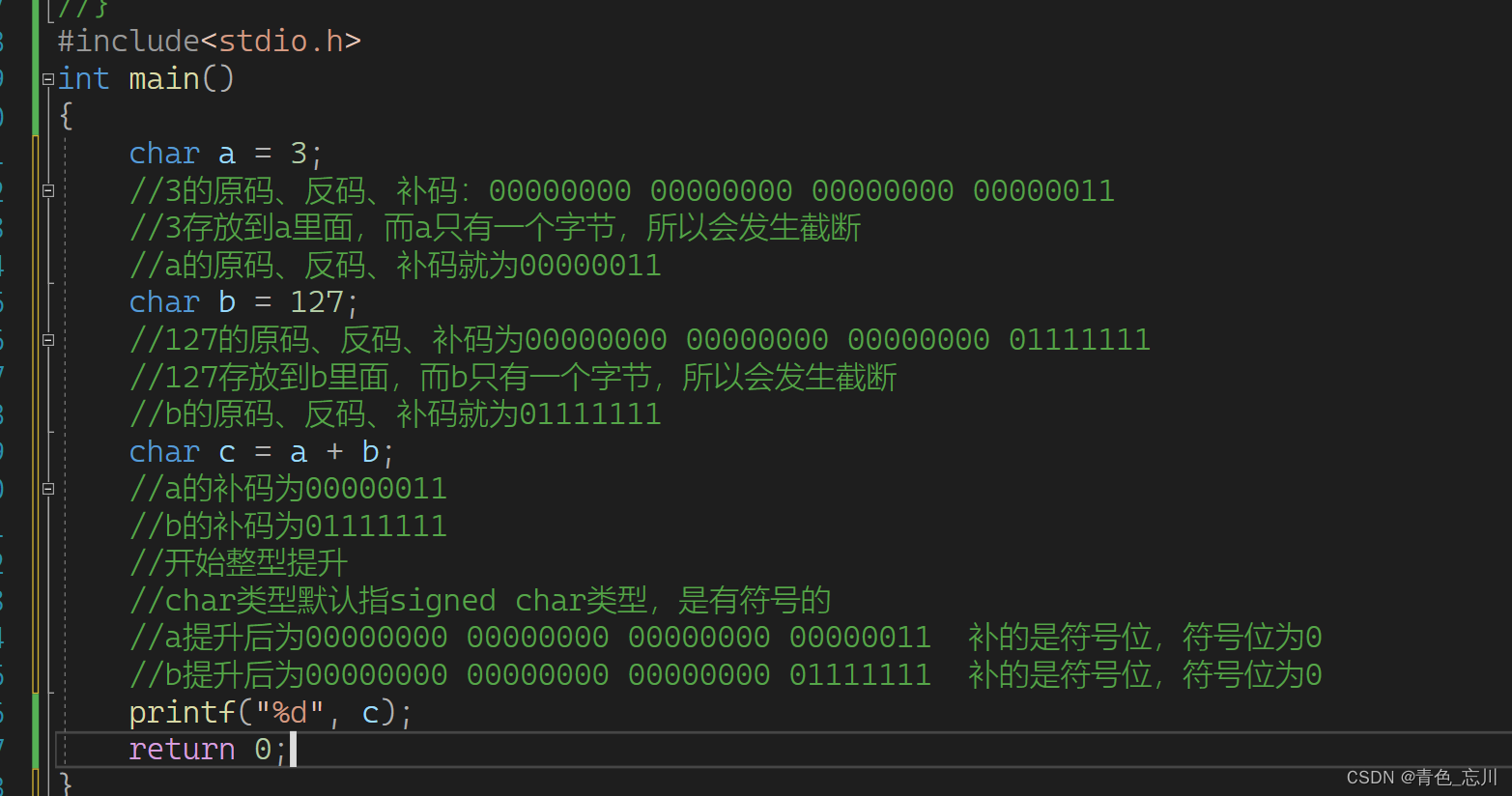
而此时由于整型提升补的是数据的符号位，我们这个char类型其实本质上应该是signed char，是有符号类型的，所以最高位就是符号位，所以补符号位，补成int类型的字节

a提升后为00000000 00000000 00000000 00000011 补的是符号位，符号位为0

b提升后为00000000 00000000 00000000 01111111 补的是符号位，符号位为0

a与b提升后相加为00000000 00000000 00000000 10000010

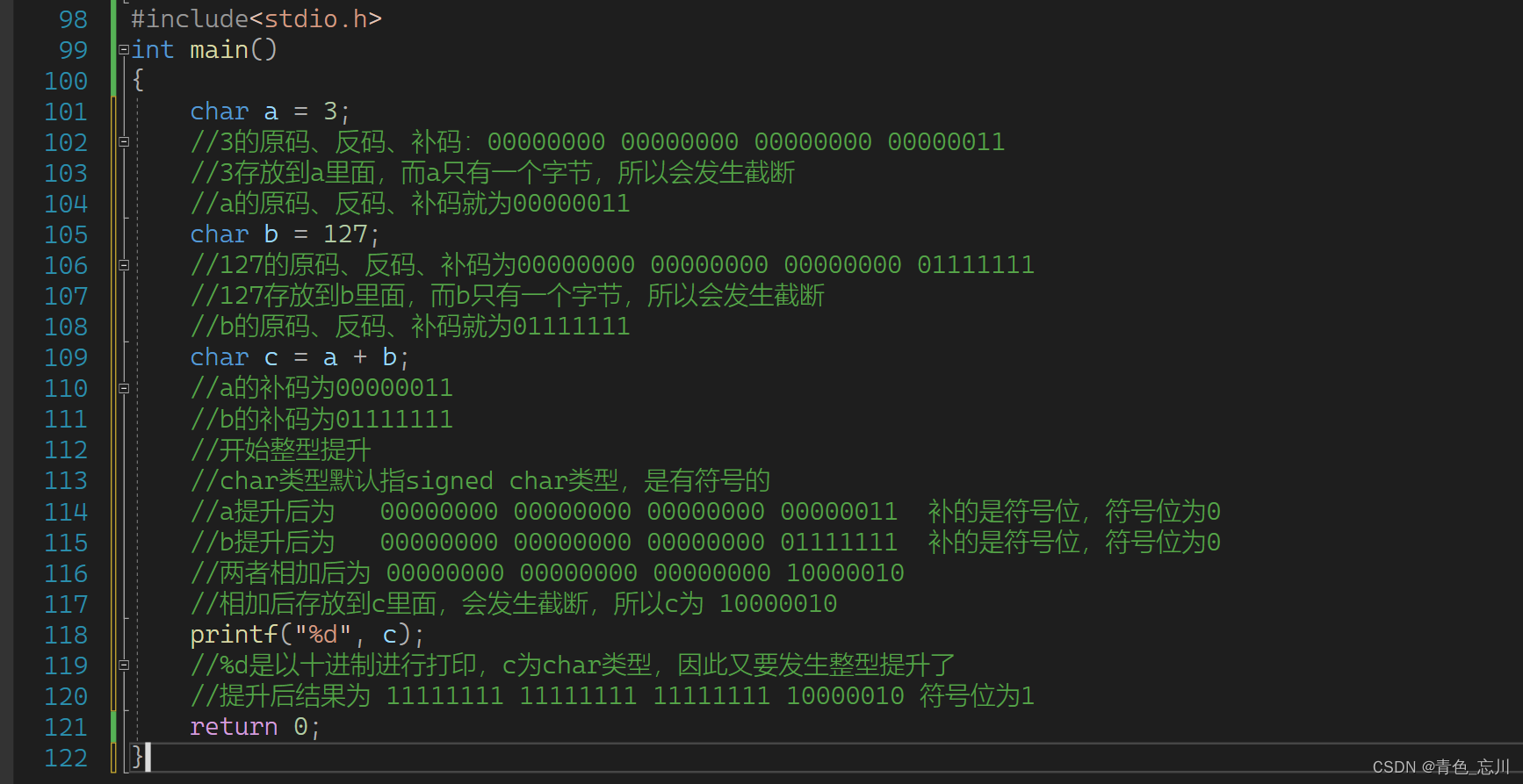
而我们相加后的结果又要放到c里面去。这里就又发生截断了

此时c为10000010

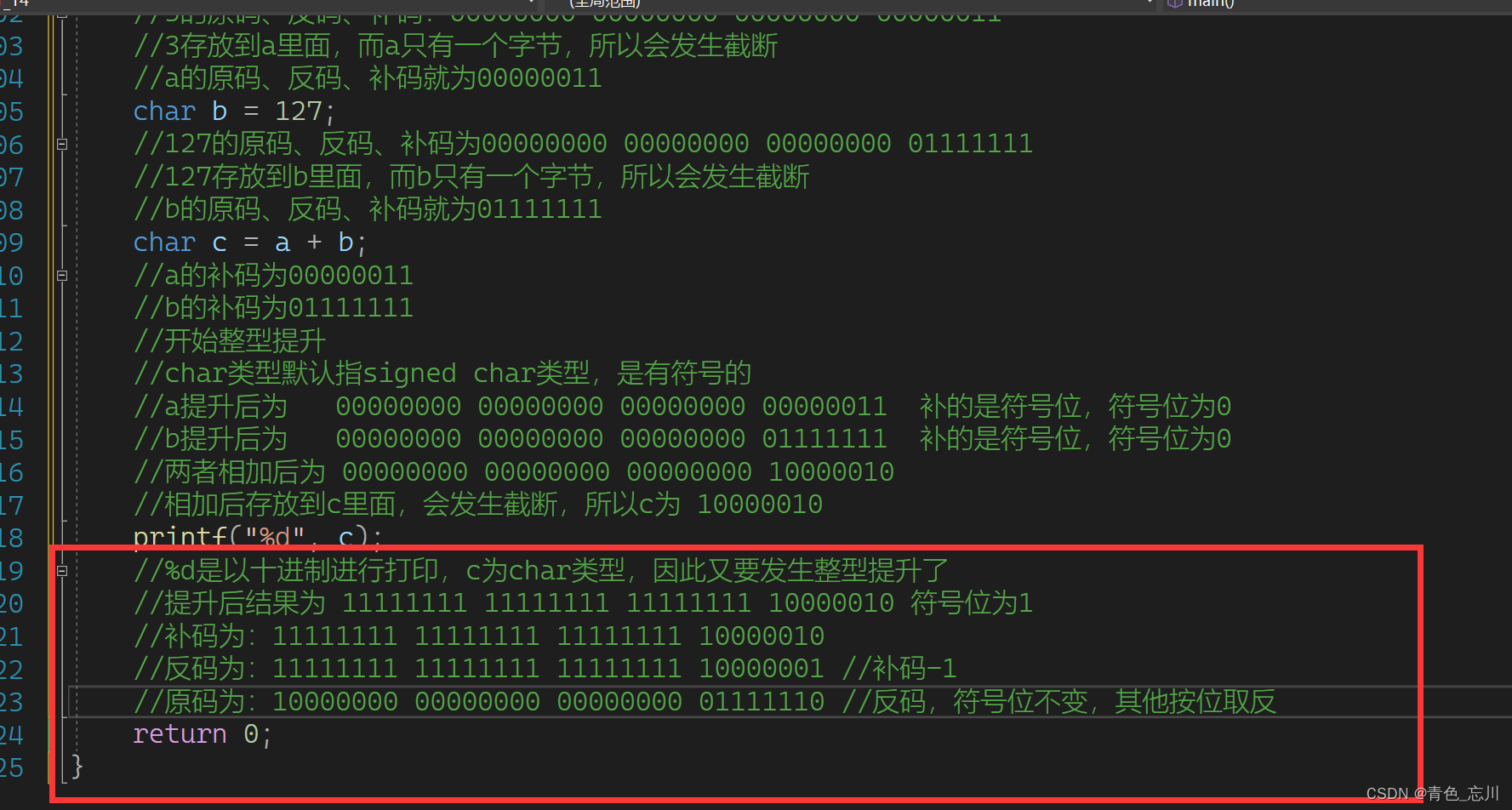
此时，接下来就要进行打印了。%d是以十进制进行打印，c为char类型，因此又要发生整型提升了，c为11111111 11111111 11111111 10000010，按符号位进行提升

要注意的是，我们的数据在内存中都是补码的形式，进行计算的，我们上述的操作都是补码，所以此时提升后的也是一个补码。既然是补码就要转换为原码了

原码为10000000 00000000 00000000 01111110

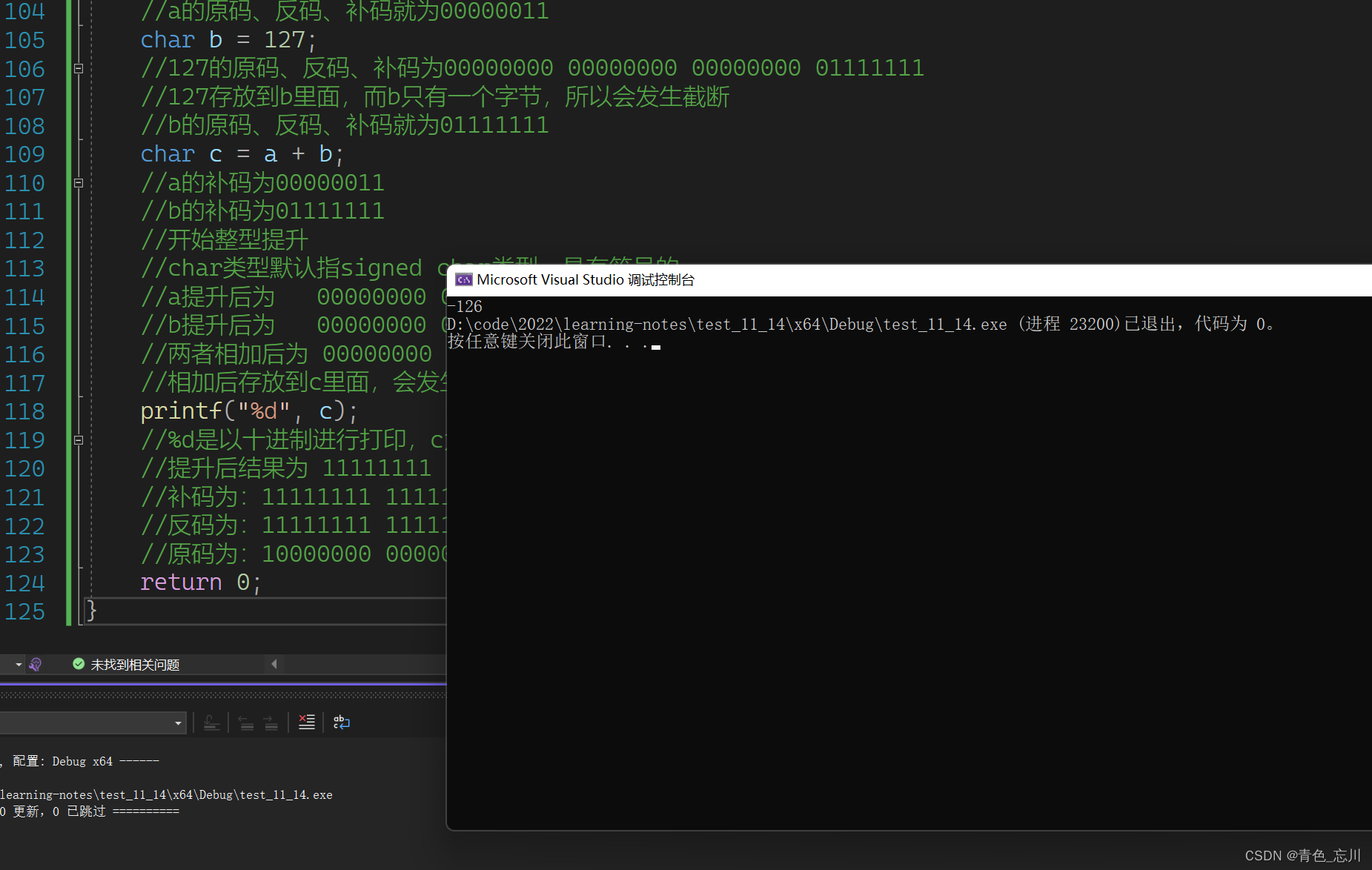
转换成十进制数就是-126

所以最终打印出来的结果就是-126

4.char类型范围有关的一些事情

char------有符号类型的char取值范围是:-128~127

无符号的char取值范围是： 0~255

那么这些范围是如何得到的呢？实际上是计算出来的，而不是规定出来的

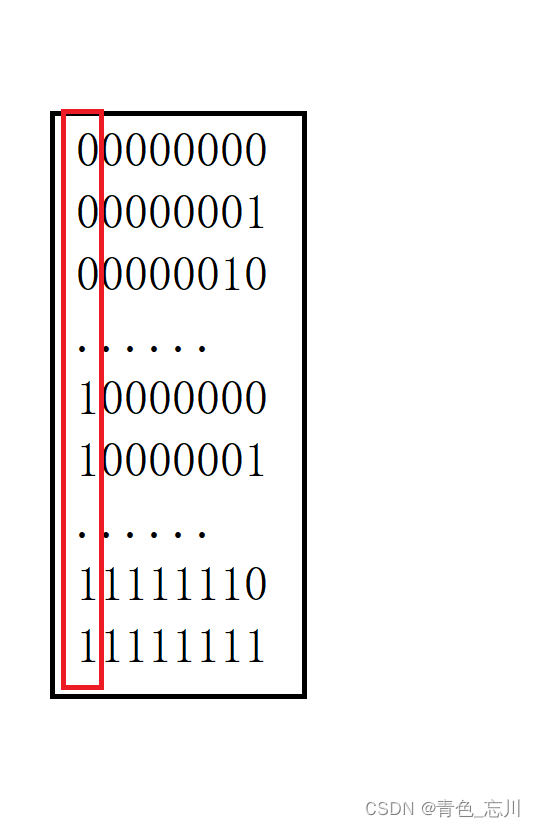
因为一个char类型是一个字节，也就是八个比特位，因此他的二进制序列的可能性就下面图中所示的这些，而这些总共有256种可能性

假设我们现在讨论的是有符号的数，在下面图中所示的二进制中，第一位代表的是符号位，0为正数，1为负数

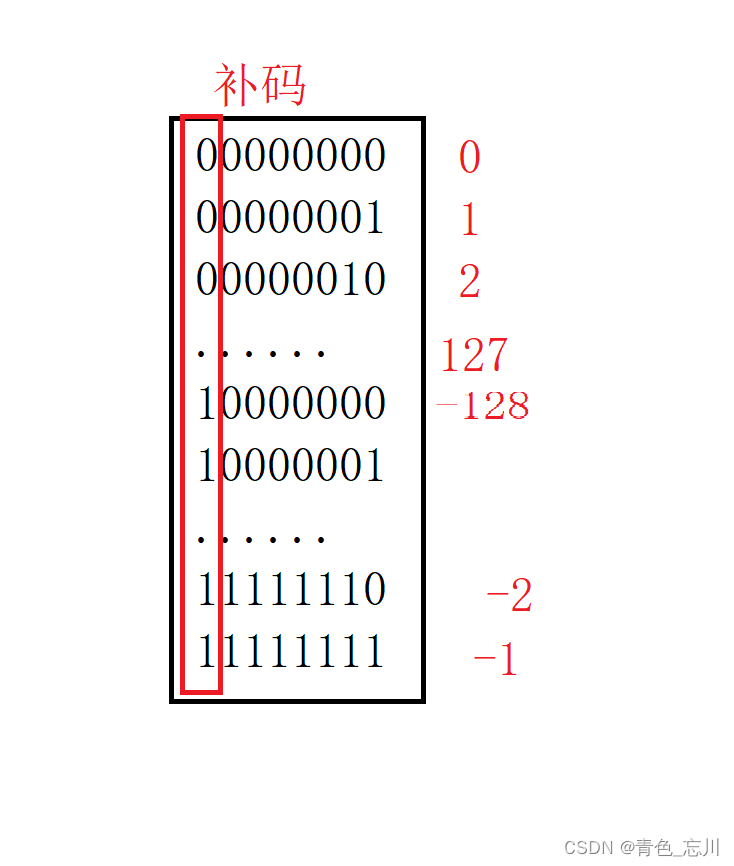
我们把这些东西存到内存中就叫做补码。然后将他们分别计算出来就是这些数

所以有符号类型的char范围就是-128~127

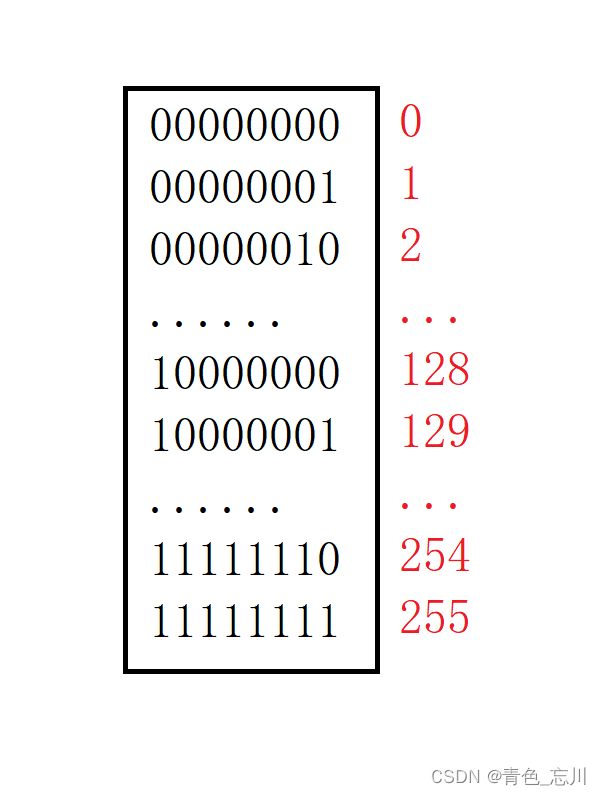
而无符号类型的就很简单了，因为他们没有负数。所以直接就是他们计算成的十进制数，如下图所示，所以他的范围就是0~255

5.有关整形提升的一些案例

我们看这段代码，并思考运行结果

#include<stdio.h>
int main()
{
	char a = 0xb6;
	short b = 0xb600;
	int c = 0xb6000000;
	if (a == 0xb6)
		printf("a");
	if (b == 0xb600)
		printf("b");
	if (c == 0xb6000000)
		printf("c");
	return 0;
}

运行结果为

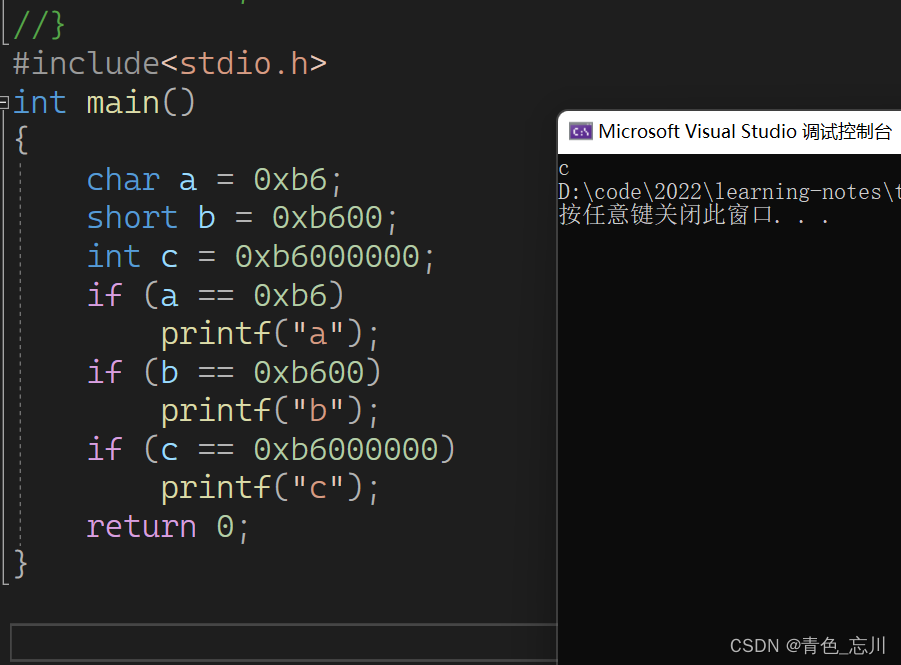
这是因为a和b他都是小于int类型的，所以都会发生整型提升。而他们的符号位都是1，所以补的都是1，肯定不一样。所以为c。（上面这些数都是16进制数。两个十六进制数代表一个字节）

还有这一段代码

#include<stdio.h>
int main()
{
	char c = 1;
	printf("%u\n", sizeof(c));
	printf("%u\n", sizeof(+c));
	printf("%u\n", sizeof(-c));
	return 0;
}

这个运行结果为

这是因为c进行了运算，所以被提升了。因为+，-也是一个操作符。

三、算术转换

小于int会发生整型提升，那么大于int呢？其实会发生算术转换

如果某个操作符的各个操作数属于不同的类型，那么除非其中一个操作数的转换为另一个操作数的类型，否则操作就无法进行。下面的层次体系称为寻常算术转换。从上到下层级依次降低

long double

double

float

unsigned long int

long int

unsigned int

int

如果某个操作数的类型在上面这个列表中排名较低，那么首先要转换为另外一个操作数的类型后执行运算。

比如

a=3；

b=3.14；

c=a+b；

那么a首先会转换成b的类型进行计算

但是进行算术转换要合理，否则会出现问题

float a=3.14

int b=a；隐式转换，会出现精度缺失，但是编译器只会报警告，不会报错

四、操作符的属性

复杂表达式的求值有三个影响的因素。

1. 操作符的优先级

2. 操作符的结合性

3. 是否控制求值顺序。

相邻操作符才考虑优先级，两个相邻的操作符优先执行哪一个？取决于他们的优先级。如果两者的优先级相同，才取决于他们的结合性

1.优先级表格

操作符	描述	用法用例	结果类型	结合性	是否控制求值顺序
（）	聚组	（表达式）	与表达式同	N/A	否
（）	函数调用	rexp（rexp，....，rexp）	rexp	L-R	否
[ ]	下标引用	rexp[rexp]	lexp	L-R	否
.	访问结构成员	lexp.member_name	lexp	L-R	否
->	访问结构指针成员	rexp->member_name	lexp	L-R	否
++	后缀自增	lexp++	rexp	L-R	否
--	后缀自减	lexp--	rexp	L-R	否
！	逻辑反	！rexp	rexp	R-L	否
~	按位取反	~rexp	rexp	R-L	否
+	单目，表示正值	+rexp	rexp	R-L	否
-	单目，表示负值	-rexp	rexp	R-L	否
++	前缀自增	++lexp	rexp	R-L	否
--	前缀自减	--lexp	rexp	R-L	否
*	间接访问	*rexp	lexp	R-L	否
&	取地址	&lexp	rexp	R-L	否
sizeof	取其长度，以字节表示	sizeof rexp sizeof（类型）	rexp	R-L	否
（类型）	类型转换	（类型）rexp	rexp	R-L	否
*	乘法	rexp*rexp	rexp	L-R	否
/	除法	rexp/rexp	rexp	L-R	否
%	整数取余	rexp%rexp	rexp	L-R	否
+	加法	rexp+rexp	rexp	L-R	否
-	减法	rexp-rexp	rexp	L-R	否
<<	左移位	rexp<<rexp	rexp	L-R	否
>>	右移位	rexp>>rexp	rexp	L-R	否
>	大于	rexp>rexp	rexp	L-R	否
>=	大于等于	rexp>=rexp	rexp	L-R	否
<	小于	rexp<rexp	rexp	L-R	否
<=	小于等于	rexp<=rexp	rexp	L-R	否
==	等于	rexp==rexp	rexp	L-R	否
!=	不等于	rexp!=rexp	rexp	L-R	否
&	位与	rexp&rexp	rexp	L-R	否
^	位异或	rexp^rexp	rexp	L-R	否
\|	位或	rexp\|rexp	rexp	L-R	否
&&	逻辑与	rexp&&rexp	rexp	L-R	是
\|\|	逻辑或	rexp\|\|rexp	rexp	L-R	是
？：	条件操作符	rexp？rexp：rexp	rexp	N/A	是
=	赋值	lexp=rexp	rexp	R-L	否
+=	以...加	lexp+=rexp	rexp	R-L	否
-=	以...减	lexp-=rexp	rexp	R-L	否
*=	以...乘	lexp*=rexp	rexp	R-L	否
/=	以...除	lexp/=rexp	rexp	R-L	否
%=	以...取模	lexp%=rexp	rexp	R-L	否
<<=	以...左移	lexp<<rexp	rexp	R-L	否
>>=	以...右移	lexp>>rexp	rexp	R-L	否
&=	以...与	lexp&=rexp	rexp	R-L	否
^=	以...异或	lexp^=rexp	rexp	R-L	否
\|=	以...或	lexp\|=rexp	rexp	R-L	否
，	逗号	rexp，rexp	rexp	L-R	是

2.运算规则

首先确定优先级，相邻操作符按照优先级高低计算

优先级相同的情况下，结合性才起作用

我们看这样一段代码

#include<stdio.h>
int main()
{
	int a = 1;
	int b = 2;
	int c = 4;

	int d = a * 4 + b / 3 + c;
	return 0;
}

这个表达式先算a*4，然后计算b/3，然后计算第一个加法，然后计算第二个加法。

3.一些问题表达式

（1）ab+cd+e*f

a*b+c*d+e*f

这个表达式种，我们按照从左到右给他分别记作 1 2 3 4 5

那么他的计算顺序可以是1 3 2 5 4

也可以是1 4 2 5 3

这就出现两种运算方式。虽然结果是一样的，但是出现了两种计算方式，这就是很危险的行为了。比如将a看作一个表达式，如果他出现了副作用，那么势必会影响结果。

（1）c+ --c

这个也存在问题，我们知道先算--，然后计算加法

但是我们计算的是2 +2 呢还是3+2

也就是说虽然运算顺序知道了，但出现了副作用的表达式。第一个c会不会改变是取决于编译器的。看他是什么时候拿出他的值的。因此这个也存在潜在的危险

（3）i=i-- - --i（i=-3）i++ + ++i

这个代码，将他放在不同的编译器上，甚至每个编译器的结果各不相同。这是极其危险的代码

（4）调用函数时

#include<stdio.h>
int fun()
{
	static int count = 1;
	return ++count;
}
int main()
{
	int anwer;
	anwer = fun() - fun() * fun();
	printf("%d", anwer);//输出多少？
	return 0;
}