1表面弛豫

2表面能的计算

3对称和非对称板块模型

4 表面重构

5表面上的吸附质

6表面覆盖效应

1表面弛豫

在上述例子中,为了建立五层原子的板块模型,将原子放置在了板块模型中。原子的位置是理想的,是 $FCC$ 材料中的体相原子位置。在体相的 $FCC$ 金属中,任何两个相邻原子的间距是定值的。但是对于靠近材料表面的原子层而言,则没有理由保持相同的原子层间距。因为与体相中的原子相比,表面处原子的配位数减少了,可以想到:靠近表面处的原子层间距应该与体相中有所不同。这一现象称为表面驰豫( $Surface Relaxation$ )而后续表面计算中的一个目标就是对该弛豫进行表征。

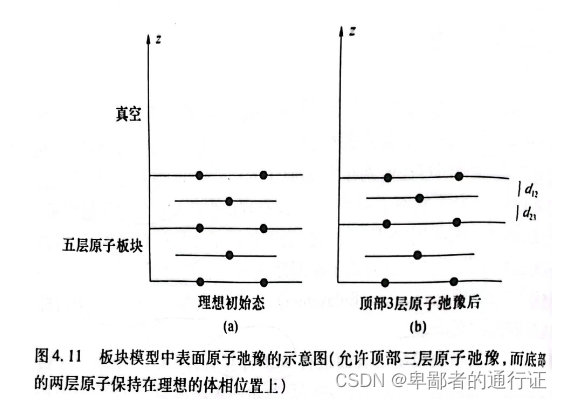
在对五层板块模型的表面进行 $DFT$ 计算时,图4.11中给出了该模型在弛豫前后的原子位置。左侧是原始的板块模型，其中的原子按体相位置排列;而右侧是顶部三层原子发生弛豫后的板块模型。表面驰豫意味着弛豫后的表面要比初始表面(理想表面)的能量更低。在对能量进行最小化后(能量与超晶胞中原子位置具有函数关系)就能够得到弛豫后的表面几何构型。可以把板块下部的原子看作是材料的体相部分,并对这些底部原子层中的原子进行约束,使其固定于理想的体相位置上。这样一来,该计算就是与原子位置呈函数关系的超晶胞总能的最小化,其中仅允许顶部几层原子移动,这就产生了如图 4.11(b)所示的结构。实际上,表面中原子移动的量级仅为 0.1A。在该图中,夸大表示了顶部原子层的弛豫量级。

在垂直于表面方向上,表面的突然终止会引发表面上原子配位关系的剧烈变化。这常常会导致第一层和第二层的原子层间距减小。最外层和次外层的距离可以表示为 $d_{12}$ ,而其豫改变量表示为 $\delta d_{12}$ 。驰豫改变量通常表示为体相材料层间距离的百分比,负值表示两层原子间距缩短,而正值表示两层原子间距扩展。在其他几个原子层之间的改变量表示为 $\delta d_{23}$ 、 $\delta d_{34}$ ,依次类推。表4.1列出了 $Cu\left ( 100 \right )$ 和 $\left ( 111 \right )$ 表面的层间距离弛豫,其中采用不同的原子层数建立板块模型。在每个情形下,都将最下方的两层原子固定在体相位置,而允许其他所有原子层弛豫。

$Cu\left ( 100 \right )$ 表面层间距的弛豫改变量更为显著，而在密排的 $Cu\left ( 111 \right )$ 表面则稍弱。对于这两个表面，计算得到的层间距弛豫改变量，均随着模型中所包含的原子层数增加而更接近于物理实验结果。使用8层的板块模型，对于 $Cu\left ( 100 \right )$ 计算的得到的弛豫改变量 $\delta d_{12}$ 是 $-2.14%$ ，或者约为 $0.036A$ 。和实验值很接近。

类似地,对于 $Cu\left ( 111 \right )$ 表面, $DFT$ 估算的 $\delta d_{12}$ 是 $-0.59%$ 或约为 $0.012A$ ;这一数值与实验值非常接近。考虑到这些位置改变量已经如此之小,因此 $DFT$ 能够很好地再现这些实验测试。

在表面弛豫的讨论中,仅仅考虑了垂直于表面方向上的弛豫。这对上述计算的描述是正确的,因为板块模型在表面的晶面内是完全对称的。因此,在该表面的晶面内作用于每个原子上力的分量恰巧为零从而在弛豫过程中,原子并不会在这个晶面内移动位置。对于真实表面而言,这点也是适用的。如果将超晶胞中该晶面内的部分,看作是这些类似于体相的原子层的复制,那么就可以明确一点:必须采用体相晶格间距来定义超晶胞,正如等式(4.1)所定义的那样。这一讨论强调了表面计算的另个尚未提及的特点,即:必须对所用晶格常数的数值进行选择。最好的方法是;使用与表面计算相同的交换关联泛函,先对体相材料进行精确收敛的 $DFT$ 计算并采用该计算所得到的晶格常数。使用任何其他的晶格常数(例如,实验测得的品格常数)会导致材料模型中出现人为应力( $Artificial Stress$ ),并会导致表面原子在物理上产生虚假驰豫( $Spurious Relaxation$ )。

2表面能的计算

如前文所述，可以通过沿某个晶面劈裂体相材料来建立表面。表面能 $\sigma$ 就是劈裂体相晶体所需要的能量。表面能计算方法的思想和依据就是：可以把这个切断过程所需的能量等效为新形成两个表面所需要的能量（假设该过程是可逆过程）。这就意味着可以根据 $DFT$ 板块设计来确定表面能，即：

$\sigma =\frac{1}{A}\left [ E_{slab-nE_{bulk}} \right ]$ (1)

式中： $E_{slab}$ 为表面板块模型的总能； $E_{bulk}$ 为体相材料单个原子或分子的能量； $n$ 为板块模型的原子或者分子个数； $A$ 为表面板块模型中的总面积（包括顶面和底面）。

在宏观角度上，表面能通常表示为 $J/m^{2}$ 这一单位。在 $DFT$ 计算中，表面能定义为电子伏特/平方埃（ $eV/A^{2}$ 更为合适，两着换算关系 $1J/m^{2}=16.02eV/A^{2}$ 。

式（1）所定义的表面能是两个量之间的差值，但是这两个值的计算方式稍有不同。对于表面部分，通常使用较大的超晶胞，包含有一个真空区，并且使用较少的k点。对于体相来说，则恰好相反。那么，怎么做才不会使两着的理论计算影响表面能结果？目前这个问题还处于研究阶段；但是经过一系列努力（相对于板块模型的原子层数、k点、截断能、超晶胞尺寸等因素进行测试、确保这两个能量都具有良好的收敛性），可以把上述问题最小化。

例如， $DFT$ 计算铜表面能如下表所示，其中所使用的板块模型和表4.1相同。 $Cu\left ( 111 \right )$ 的表面能比 $Cu\left ( 100 \right )$ 要低，意味着 $Cu\left ( 111 \right )$ 要比 $Cu\left ( 100 \right )$ 要稳定。这一结论与现实相符：简单材料最稳定表面通常是原子密度最大的表面。通过该表面能计算结果与一个实验观测值相比较，可以清楚的看到上述 $DFT$ 计算能够给出该表面较为精确的数值。

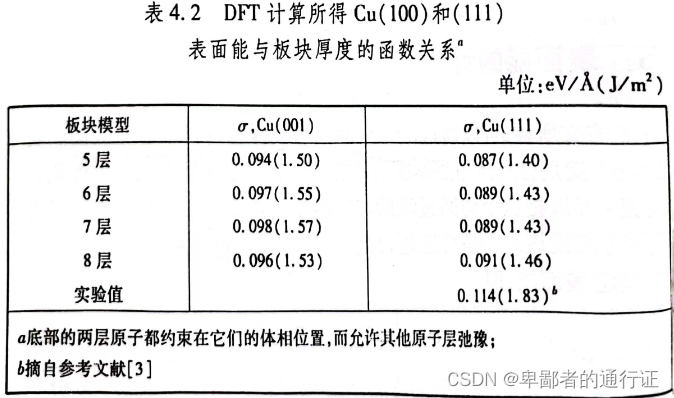
在表4.1和表4.2结果中，显著区别在于：前者所需要更多的层数来收敛逼近真实结果。这揭示一个思想：“收敛性”并不是一个可以同等的对应于所有物理特性。意思就是：经过一系列计算，可能对于某个物理量的结果已经趋近于收敛，但是这个体系其他物理量并没有达到收敛的程度。在原子层弛豫计算中，仅为 $0.02A$ 的层间距改变量，就会导致 $\delta d_{12}$ 为 $1%$ 。这意味着：对于确定表面模型中原子的精确几何构型而言，这是一个非常敏感的物理指标。也可以看出，表面能对于对于构型变化没那么敏感。

3对称和非对称板块模型

回顾一下图4.1所示 $FCC$ 材料的 $5$ 层板块模型，其中在对该模型进行弛豫时，仅选择顶部的三层原子可以弛豫，保持下部的两层原子固定在体相上。这种方法所定义的是一个非对称性板块模型，一侧原子可以弛豫，一侧的原子可以弛豫，模拟表面；另一层原子层保持固定，模拟体相区域。非对称性板块模型的另一个重要特点就是：该表面在随后的研究过程中会产生一个偶极子（ $Dipole$ ）。如果想要研究原子或者分子在表面上的吸附，这一点就很重要。当将周期性边界条件应用于包含有这个非零偶极子的超晶胞时，这个偶极子与其上下方原子产生静电作用，从而会对总能产生一部分贡献。在周期性体系中，产生这个静电作用是合理的，但是如果描述的是一个隔离态表面，这个静电作用是虚拟的。许多 $DFT$ 计算程序都已经采用了相关方案，消除了对非零偶极子模型应用周期性边界条件所引发的人为虚拟静电场。通常做法是，能够计算得到偶极子，然后应用一个相等且相反的偶极子，从而矫正真空区局域电势。

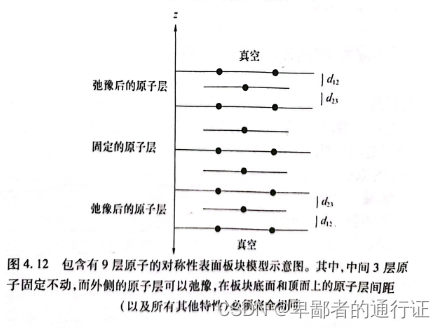
另一个方法就是采用对称性模型来描述表面。在对称性模型中，板块中心存在一个镜面。中心处的原子层的原子通常是固定在体相结构，允许上方和下方原子层弛豫。对称性模型一个优点是：表面上所产生的任何偶极子都会自动抵消掉。这样做也需要一定成本，因为相比于非对称性板块，在对称性板块中通常需要包含更多的原子层数。图4.12显示了一个具有9层原子的对称性板块。在下图中，板块每一端都允许三层原子弛豫。前面的5层原子板块模型的一侧允许三层原子弛豫。因此为了在计算中允许三层原子弛豫，就需要在对称模型中包含9层原子，非对称模型只需要5层原子。

4 表面重构

前面提到由于存在表面弛豫，导致形成表面的原子间距与体相并不相同。需要说明的是：如果仅仅允许表面进行弛豫，也许并不能由 $DFT$ 计算得到足够精确的信息。例如在许多表面所经历的重构 $\left ( Reconstruction \right )$ 中，表面原子形成了新键。

表面重构一个非常明显的例子就是 $Si\left ( 100 \right )$ 表面。硅、碳和某些其他第四主族材料的元素的体相是金刚石结构。在这种结构中，每个原子都与他最近的4个近邻原子以四面体排布成键。如果沿着 $\left ( 001 \right )Miller$ 晶面劈裂，则在表面上硅原子具有两个最紧邻原子，而非4个，如下图所示。图示的材料表面已经完成了严格定义，可以像之前对 $Cu$ 表面所用的方法那样，对其表面原子进行 $DFT$ 弛豫。图 $4.13$ 中的图像就是这样得到的。

从化学的角度来看， $Si\left ( 001 \right )$ 的体相封端并不合理，因为每个硅原子都有对应于一个未配对电子的两个悬空键。可以想到，表面原子应该倾向于向某个位置移动，从而使未配对电子与其他未配对电子相互配对形成新键，尽管这样做会使表面上现有的原子键产生新的应变。表面原子通过配对进入到能量更为稳定的状态。下图显示了重构后 $Si\left ( 100 \right )$ 表面的俯视和侧视图，其中相邻表面原子相互作用变得更加紧密，并形成新键。图4.13和图4.14均为完全弛豫后的 $DFT$ 结构，两者之间能量差值约为 $0.7eV$ ,这个能量差值相当大。在表面上形成的长排配对原子称为二聚体排列（ $Dimer Rows$ ）。

理解了表面重构在自然界中确实存在，则由该论断所引出的关键点就是：如果在计算使用 $Si$ 的体相封端作为初始构型，则图4.14所示的 $Si\left ( 001 \right )$ 重构不会自发出现。用优化程序的计算语句描述的话，表面的重构所定义的是全局性的表面能量最低点，而体相封端表面会产生一个不同的局域性能量最小值；无法用一组 $DFT$ 计算证实所研究的表面没有重构。

接下来,作为一个警诫性的例子,再来介绍另一个 $Si$ 表面, $\left ( 111 \right )$ 表面。使用与上文相同的化学推演方法,不难确信这个表面也会以某种方式发生重构。如果着眼于“预测”该重构的细节信息可以将表面上的悬空键以各种可能的组合方式连接在一起,进行一系列的计算。在经过许多繁复的这类计算之后,哪一种结构中每个表面原子所具有的平均能量最低,这种结构就是所得到的“预测”结果。可以先对 $Si\left ( 111 \right )$ 的单个单胞( $Single Unit Cell$ )进行计算,如果想要做得更多更好,可以尝试使用更多的单胞进行计算。在 $7\times 7$ 个单胞中, $Si\left ( 111 \right )$ 的稳态重构包含着错综复杂的原子排列。这是在收集到大量实验数据的基础上,并且需要用实验数据来指导计算。

5表面上的吸附质

上面都是对表面化学成分与体相化学成分相同的情况。但是现实中存在很多表面出现其他化学物质的情况。本节值只讨论原子或者分子化学吸附于表面。

可以运行一些计算来理解 $H$ 原子是怎样结合在 $Cu\left ( 100 \right )$ 表面上的。许多有关金属的化学反应，都可以形成单个 $H$ 原子。因此，为了对这类反应进行描述，就必须了解这些原子在表面上的特点。那么在表面上的 $H$ 原子到底倾向于处于何处？如果对 $Cu\left ( 100 \right )$ 表面来探讨这个问题，则存在几个具有特殊对称性的位置，直观上看，这些位置很有可能成为 $H$ 的潜在结合位置(如下图所示）。

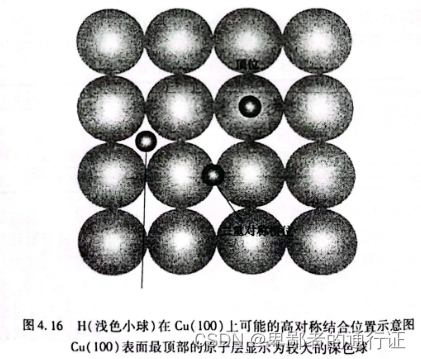
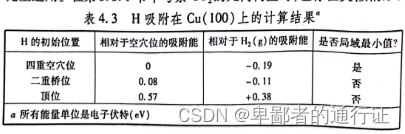
关于如何用计算来描述 $H$ 在图4.16 中的每位置。先定义一个超晶胞包含有 $Cu\left ( 100 \right )$ 的板块模型,将一个 $H$ 原子放置在相对接近于表面顶层的某个图示位置处,然后最小化体系的能量并允许几个原子层和 $H$ 原子的位置发生弛豫。对类似于这样的一组计算,可以地比较其总能来确定最有可能的位置,因为它们总能的差值也就相当于在表面不同位置移动 $H$ 原子消耗(或得到)的能量。表4.3 给出了这组计算的结果。这些计算预测了 $H$ 在四重空穴位更加稳定,但是,二重桥位的能量仅高了 $0.08ev$ 。因为在室温下热能的典型单位是 $k_{b}T\sim 0.03eV$ ,这些结果表明;至少在某些情形下 $H$ 可能在这两种位置上都存在。

此外，对于这些结果，有必要验证一下根据该体系实际上的局域能量最低值所得到的原子构型。为了说明这一点，以上图中顶位（ $On-Top Site$ ）上的力矩为例。对于正好处在表面 $Cu$ 原子上方的 $H$ 原子，根据对称性，在平行于金属表面的平面内，作用在这个 $H$ 原子上的力必定为0。这意味着，在优化计算过程中， $H$ 原子将会始终位于 $Cu$ 原子的正上方，虽然将其移走可能会降低其能量。但其实，上面的三种位置都处于高对称性位置，上面的论断对于三种位置都适用。

可以通过偏移一点位置来打破这种对称。一个简单的办法就是：先将 $H$ 原子沿任意方向移动一个微小距离（如 $0.2A$ ），且移动方向不再与表面上的对称方向一致，然后重复上述计算。最后发现，采用这种计算方法，如果 $H$ 原子在上述任意一个高对称性位置偏移 $0.2A$ ,则在弛豫后原子都会位于四重孔穴位置，即便是初始位置更烤金鱼顶位或者桥位。这表明顶位或者桥位并不是该体系能量最低点。

到此为止，可以由计算得到在 $Cu\left ( 100 \right )$ 表面上 $H$ 原子所倾向处于的位置。但另一个问题是，在这个表面上，相比于其他一些位置，这些原子处于优先位置上的倾向到底有多强烈？通常可以通过计算物质在表面上的吸附能来回答这个问题。对于吸附能，可以对其定义为：

$E^{atomic}_{ads}=E_{H/surf}-E_{H\left ( g \right )}-E_{surf}$ (2)

这里，右侧三项分别是表面吸附了 $H$ 之后的总能、在气相中单个 $H$ 原子自身的总能以及洁净表面的总能。简而言之，这个物理量是将 $H$ 原子从表面上拉脱下来，并使其进入气相这一过程所需要的能量。这个定义简单易用，但在化学上不符合规律，因为 $H$ 原子不可能长时间存在。一个更具物理含义的量就是：将 $H$ 原子从表面上拉脱开来并形成一个气相 $H_{2}$ 分子的能量这一过程所增加或者减少的能量，即：

$E_{ads}=E_{H/surf}-\frac{1}{2}E_{H_{2\left ( g \right )}}-E_{surf}$ (3)

这个吸附能与（2）式定义的数值完全不同，因为在 $H_{2}$ 分子中存在相当大的键能。 $H$ 在 $Cu\left ( 100 \right )$ 表面上上的吸附能，以及根据式（4.4）定义的吸附能分别位于表4.3的左侧和右侧。负值表明：相比于洁净表面和和一半。可以观察到，四重对称位置在热力学上更加优先。尽管表面上的另外两种位置并不是 $H$ 原子的局域最小值，但是仍然可以使用式（4.4）描述他的能量。所计算的最终能量高低也决定了最终这个体系处于平衡态各个位置出现 $H$ 原子的概率。

由上述可以自然联想到，可以用这个方法预测分子在表面上的吸附。如果想要描述氢氧根在 $Cu\left ( 100 \right )$ 表面的吸附，则需要对该位置在表面上的一系列可能位置分别计算吸附能。与上述原子态氢计算不同，对氢氧根计算不仅需要考虑物质在表面的结合位置，也需要考虑 $O-H$ 键相对于表面位相的关系。与原子吸附相类似，对于简单物质的计算，常见额失误之处就在于只考虑高对称性构型位置，例如 $O-H$ 键垂直于表面的构型。随着吸附于表面的尺寸分子增大，表面吸附分子所形成的构型方式也会增加。在许多情形下，分子都含有较多的原子，很难完全确定最优吸附构型。

6表面覆盖效应

在表4.3中，列出了计算得到 $H$ 在 $Cu\left ( 100 \right )$ 表面的吸附能（相对于气相 $H_{2}$ 分子）。在之前给出的计算结果中，忽略了一个重要因素，就是表面覆盖效应。因为使用了周期性边界条件，将一个吸附质放置在超晶胞中，自然也就意味着：每个吸附质都能在与他相邻的每个超晶胞内“观察到”一个他的复制品。这一现象可以归结为：在建立一个带有吸附质的表面超晶胞时，实际上必须描述为一个周期性的、规则性重复法的表面覆盖层。

这里存在两个问题。首先，在超晶胞计算中的吸附质一定具有长程规则排布样式，该样式与超晶胞一样不断重复。在周期性边界条件下，不可能建立吸附质的任何一种真实的无序排列模型。幸运的是，在自然界中，晶体表面上的吸附质大多是长程有序的，特别是在较低的温度下，因此能够用 $DFT$ 计算模拟很多的真实体系。

第二个问题是，超晶胞的尺寸决定了吸附质之间的距离。如果超晶胞较小，则定义了一个具有高密度（或覆盖率）吸附质的表面。如果超晶胞较大，则定义了一个具有较低密度吸附质的表面。当每个表面原子都存在一个吸附质时，则称该吸附层的覆盖率为1单分子（原子）层。如果平均两个表面存在一个吸附质，则覆盖率为 $0.5ML$ ，以此类推。

由于覆盖层的对称性，已经形成一套命名体系。下面给出一些具有代表性范例。

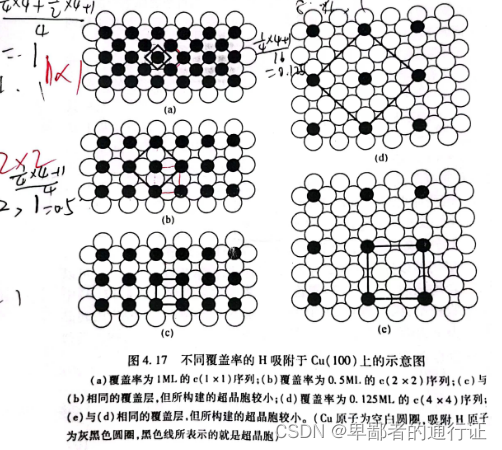
在图4.17 中,给出了几个 $H$ 吸附在 $Cu(100)$ 上的例子。先从其中的三个示例开始介绍:从图4.17 $\left ( a \right )$ 到 $\left ( b \right )$ 再到 $\left ( d \right )$ 覆盖率从 $1ML$ 降低到 $0.5\sim 0.125ML$ ,这三个覆盖层的命名分别是 $\left ( 1\times 1 \right )$ 、 $c\left ( 2\times 2 \right )$ 和 $c\left ( 4\times 4 \right )$ 。观察一下图中这些超晶胞的边长,并比较一下沿着每个边长方向吸附质的数量,可见以这种方式命名这些晶胞是河狸的。这些命名名称中的字母“ $c$ ”表示“中心（ $center$ ）”,意思是在这个超晶胞中心处,以及边角处各有一个吸附质原子。在本例中 $H$ 原子位于孔穴位,但它们也可以全部放在顶位或桥位,或其他位置而覆盖层仍然以完全相同的方式来命名。比较图 $\left ( b \right )$ 和 $\left ( c \right )$ 可以看到二者均描述了 $c\left ( 2\times 2 \right )$ 覆盖层,二者间的区别就是图 $\left ( c \right )$ 中的超晶胞较小,因而所需要的计算成本较小;给出图 $\left ( b \right )$ 中的超晶胞就是为了表明:为什么对这种覆盖层使用 $c\left ( 2\times 2 \right )$ 这个名称。类似的关系也存在于图 $\left ( d \right )$ 和 $\left ( e \right )$ 之间。

现在回顾一下这个问题：不同覆盖率是否会使计算得到的吸附能有所不同。分别针对几个不同的覆盖率，使用 $DFT$ 计算得到 $H$ 原子在 $Cu\left ( 100 \right )$ 上孔穴位的吸附能。如下表所示：

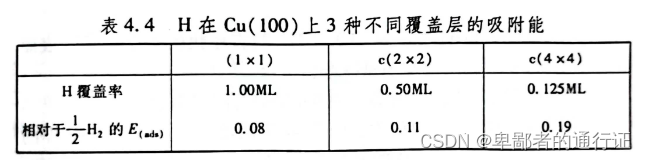
可见，在吸附 $H$ 原子的空间越大，则吸附能有所降低。对于 $c\left ( 4\times 4 \right )$ 覆盖层，是图示模型覆盖率最低的，他的吸附能也最低，因此是最优先出现的情况。 $\left ( 1\times 1 \right )$ 覆盖层中 $H$ 原子占据着 $\left ( 100 \right )$ 表面上每个孔穴位，相对于气相 $H_{2}$ ,在热力学上是不优先的。对于大多数计算，不能忽略相邻吸附质的影响。这个例子表明：描述一个原子或者分子在表面上的吸附能，重要的是先确定覆盖率和吸附质的对称性，从而最终完全定义所需考虑的体系。