计组2.2
- 定点数和浮点数
- 定点数
- 无符号数
- 有符号数的定点表示——定点整数和定点小数
- 移位运算
- 1.算术移位
- 1.原码算数移位
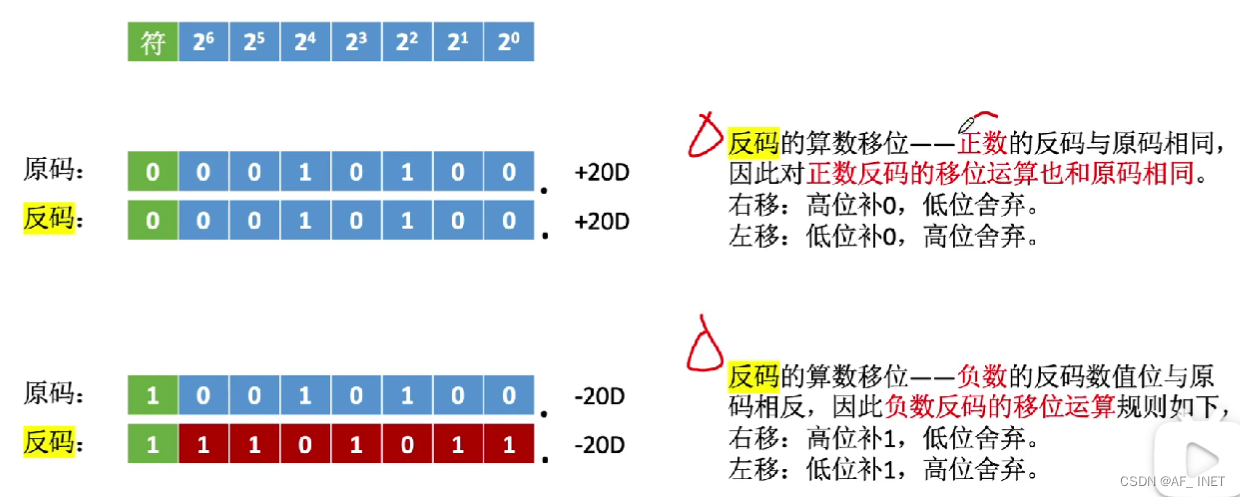
- 2.反码算数移位
- 3.补码算术移位
- 4.计算机硬件的乘法是基于算数移位和加法完成的
- 2.逻辑移位
- 3.循环移位
- 加减运算溢出判断
- 硬件判断溢出
- 法一:单一符号位
- 法二:双高位判别法
- 法三:双符号位
- 防止溢出:符号扩展
- 乘法运算
- 原码一位乘法:
- 补码的乘法:
- 除法运算
- 原码除法:恢复余数法
- 原码除法:加减交替法
- 强制类型转换
- 数据的存储和排列:
- 1.大小端模式
- 2.边界对齐
定点数和浮点数

定点数
无符号数

有符号数的定点表示——定点整数和定点小数
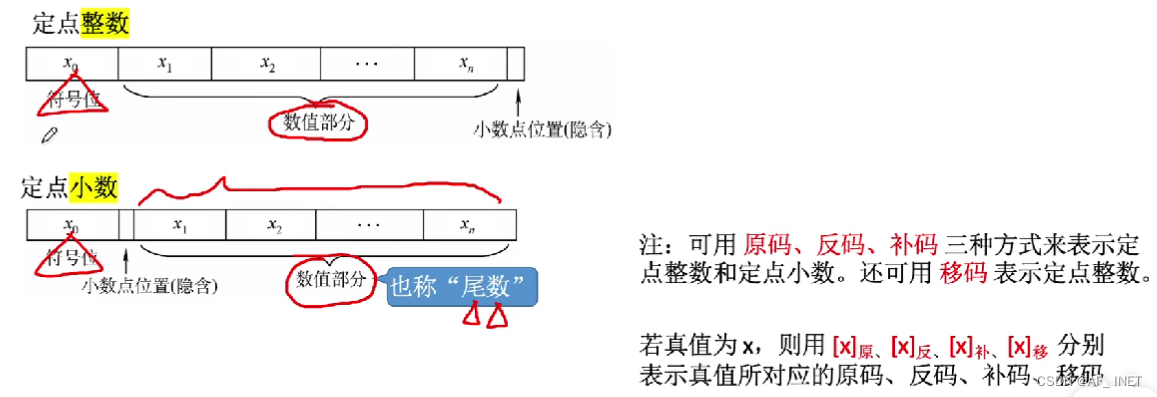
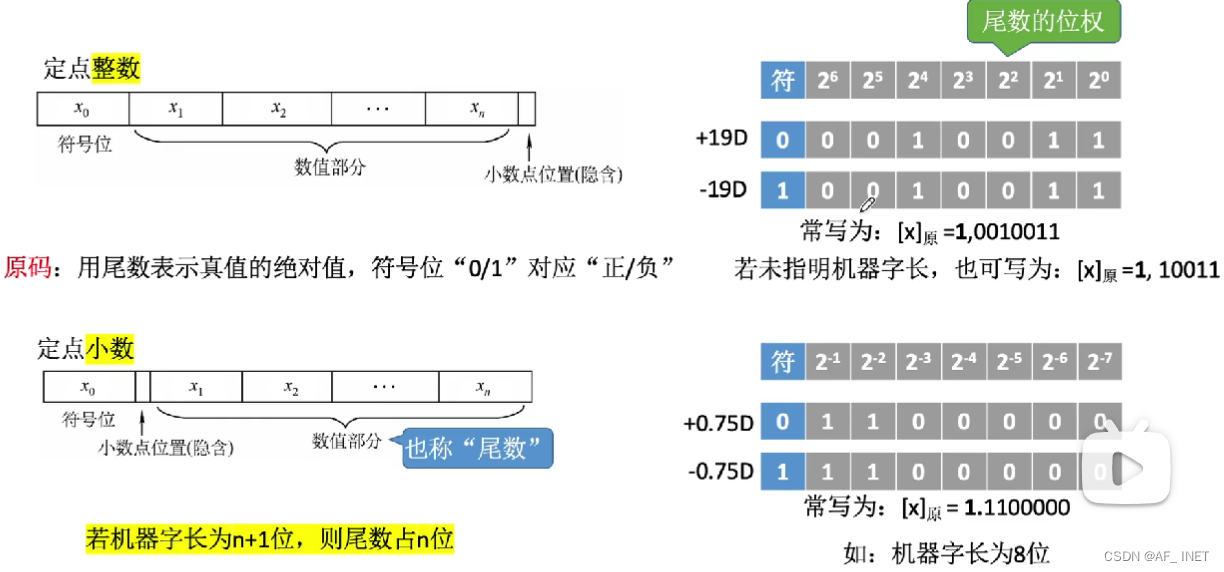
n(数值部分)+1(符号位)


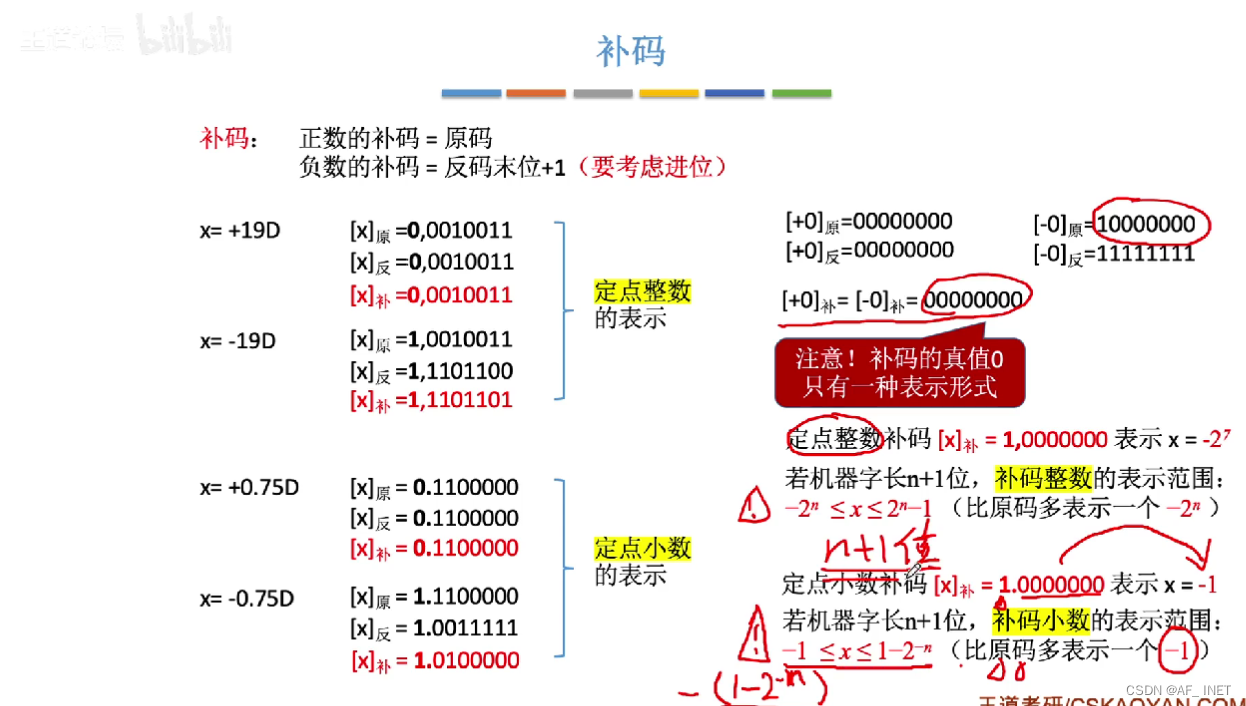
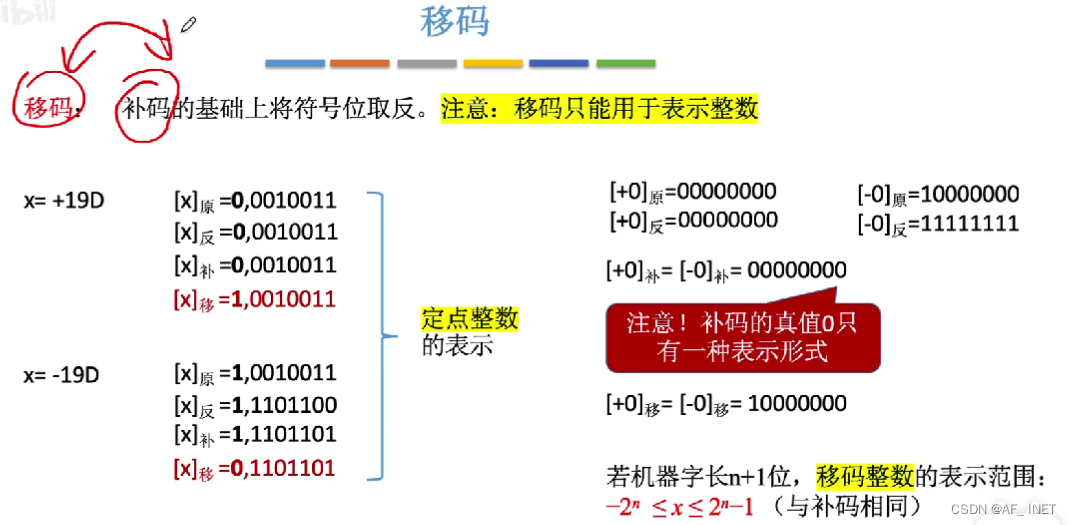
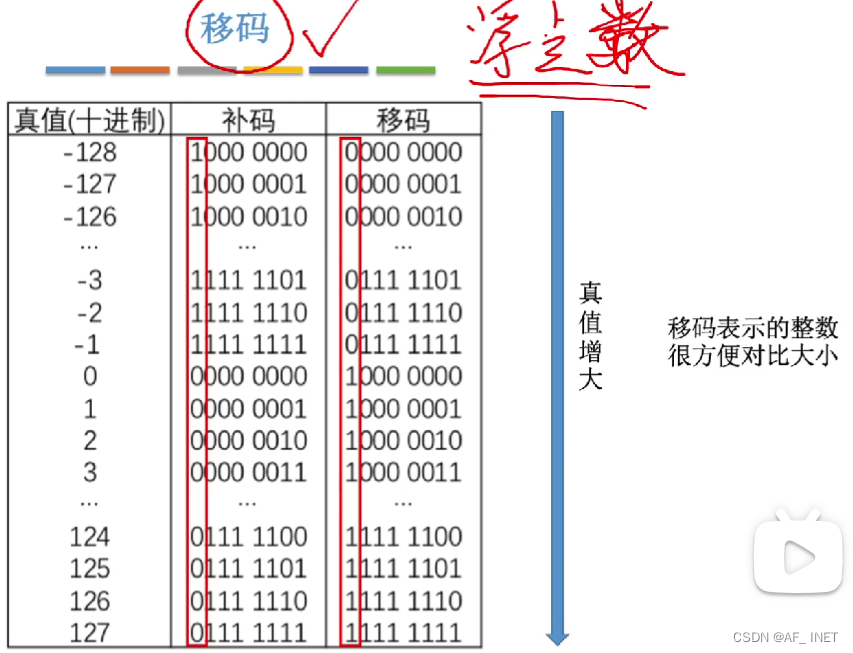
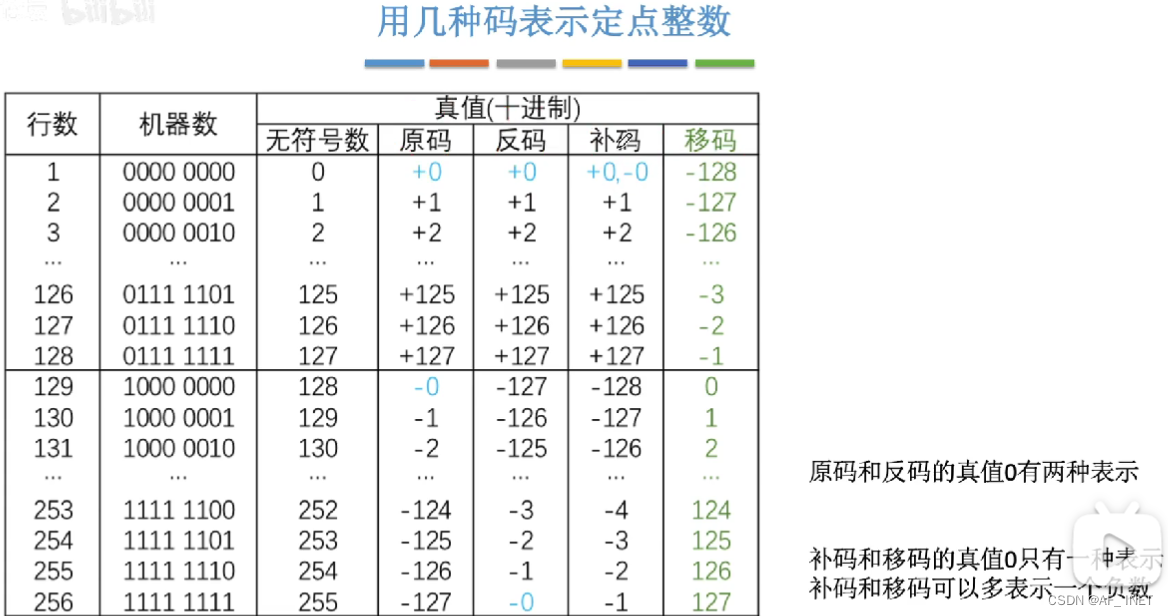


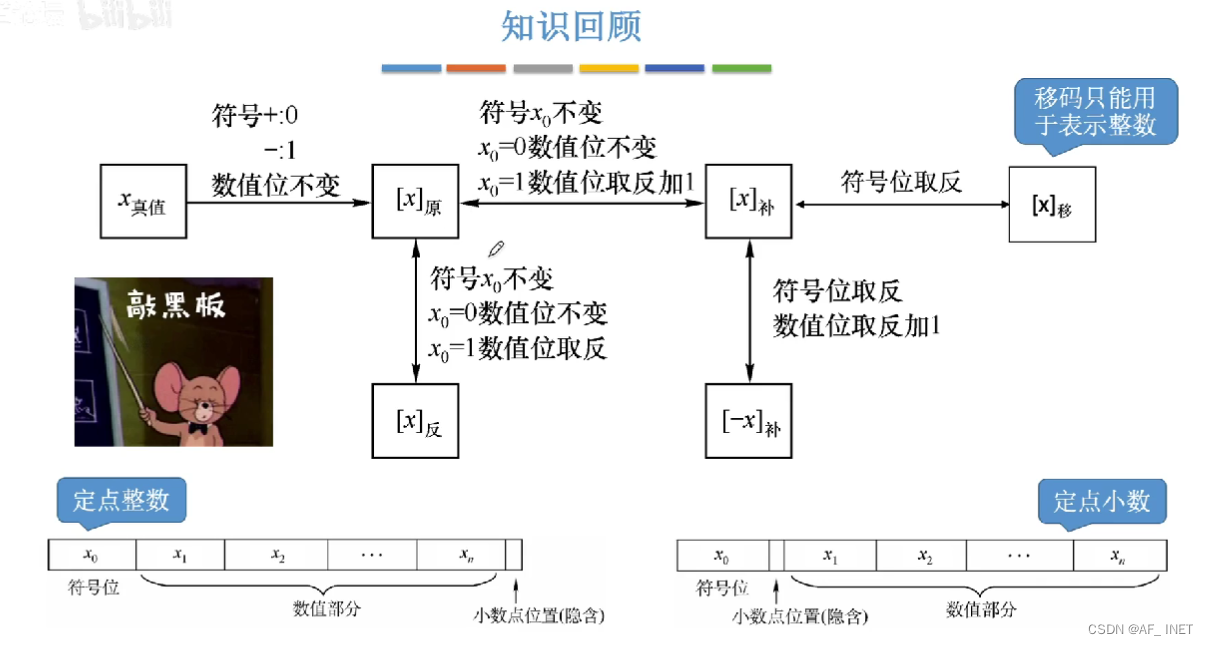

用加法代替减法
计算12进制的10-3
10-3=7
10+9=19 19%12=7
-3%12=9
9%12=9

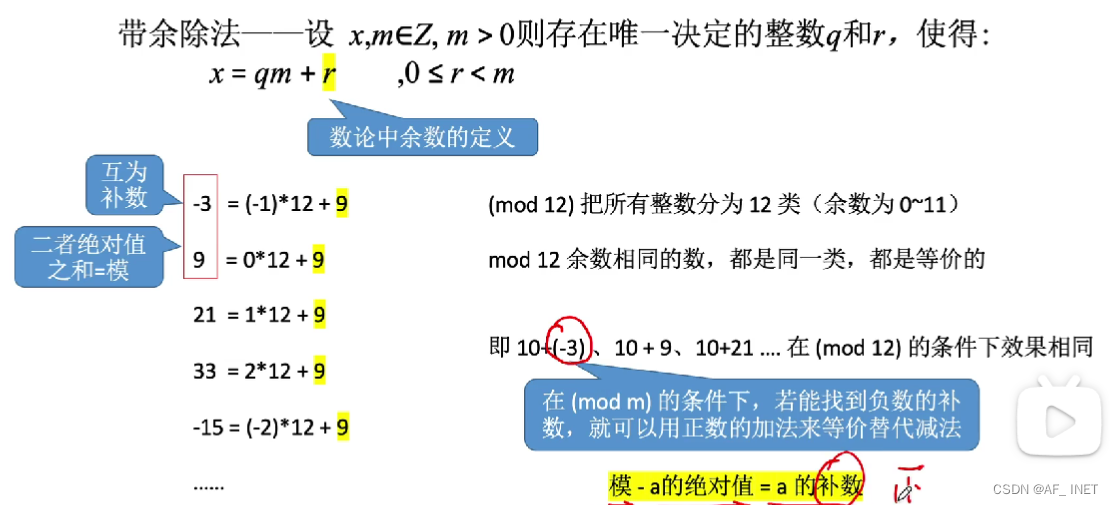
计算机如果是8bit字长,那么就天然决定了计算机所有的运算都是mod2^8的条件下进行的
使用原码计算需要减法器,减法器硬件电路复杂,用补码将减法转变为加法,找到负数的补数
移位运算
1.算术移位
通过改变各个数码位和小数点的相对位置,从而改变各数码位的位权。可用移位运算实现乘除
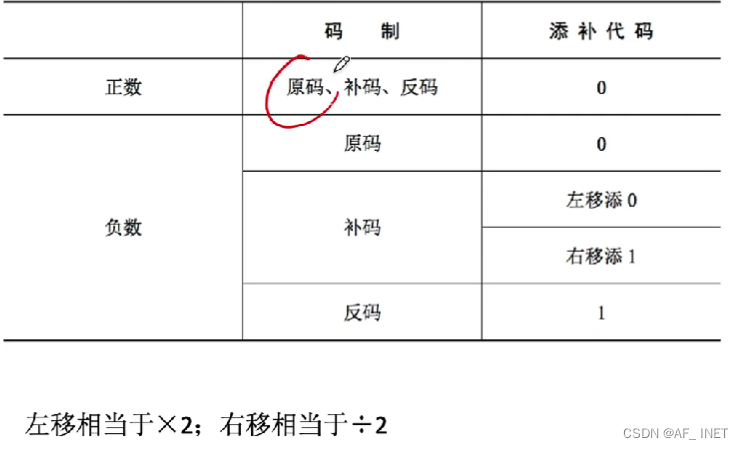
1.原码算数移位
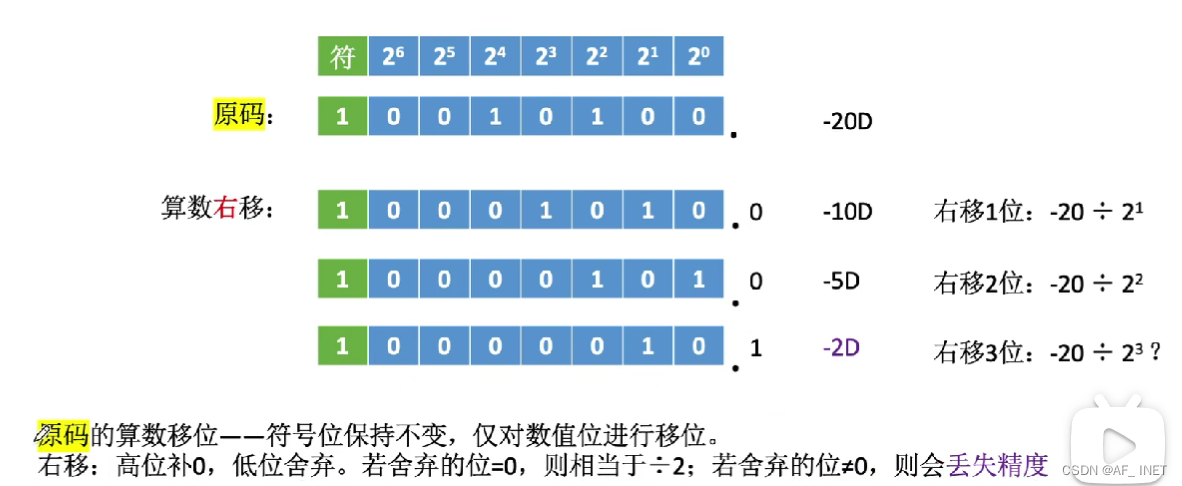
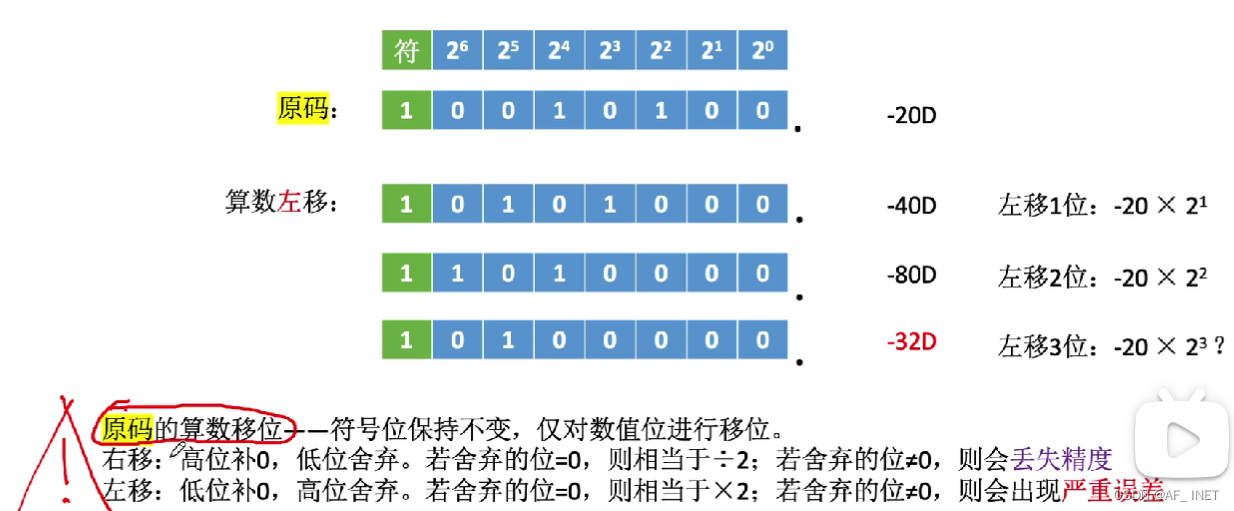
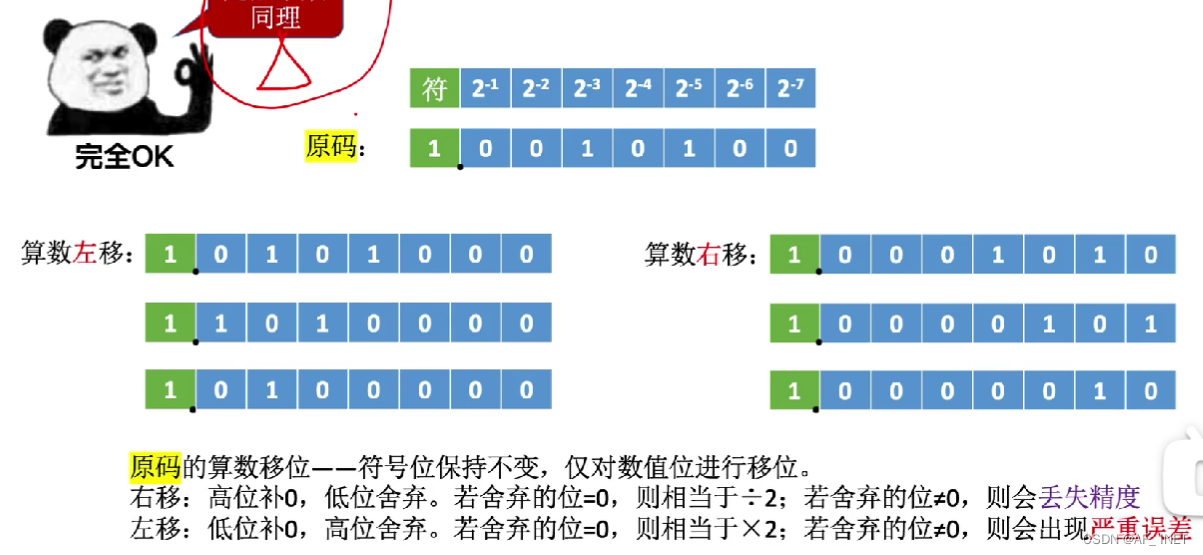
2.反码算数移位
3.补码算术移位
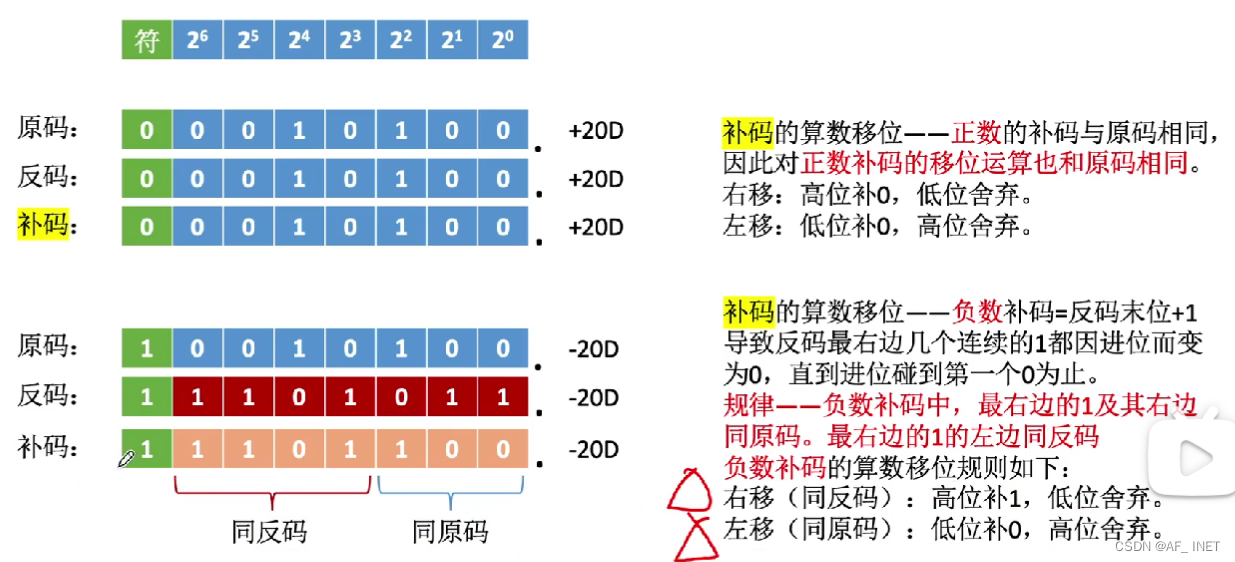
补码的算数右移/2
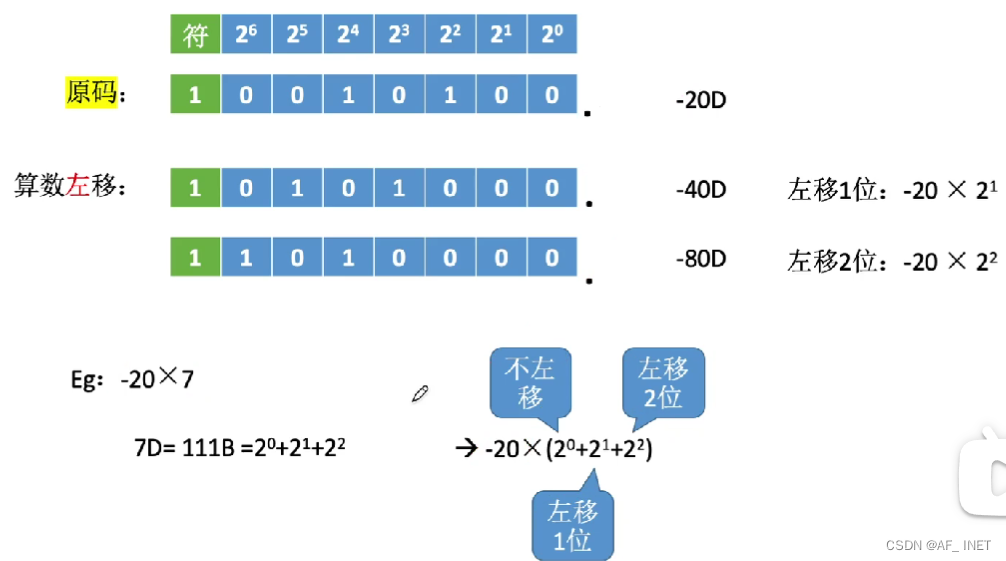
补码的算数左移*2
位数有限,有时无法用算数移位精确等效乘除法
4.计算机硬件的乘法是基于算数移位和加法完成的
2.逻辑移位
应用:将RGB代表的三个字节的数连成整体,就是让RGB三个字节分别左移16字节,8字节,0字节再相加
3.循环移位
适合把一个数据的高字节和低字节互换
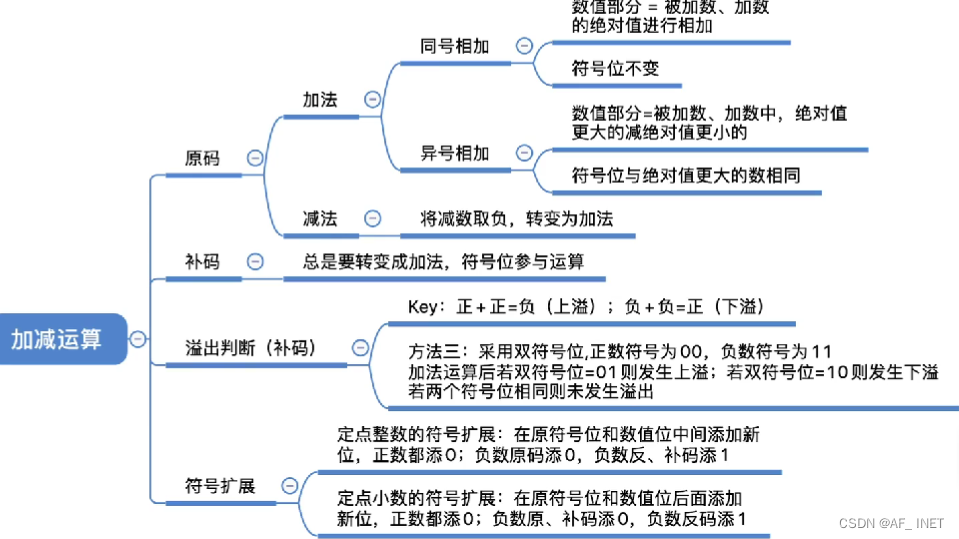
加减运算溢出判断


超出边界后,从左边到右边
硬件判断溢出
法一:单一符号位

与门或门非门可以设计硬件电路
法二:双高位判别法

注意最高数值位、符号位、进位位
本应该得到正的,实际得到负的——>上溢
本应该得到负的,实际得到正的——>下溢
法三:双符号位

更高的符号位表示本来应该得到的正负性,第二个符号表示实际的到的正负的结果

双符号位补码11,1110111逗号前面看作20 , 21,所有的都是小于22=4,所以称为模四补码,单同理符号位
防止溢出:符号扩展
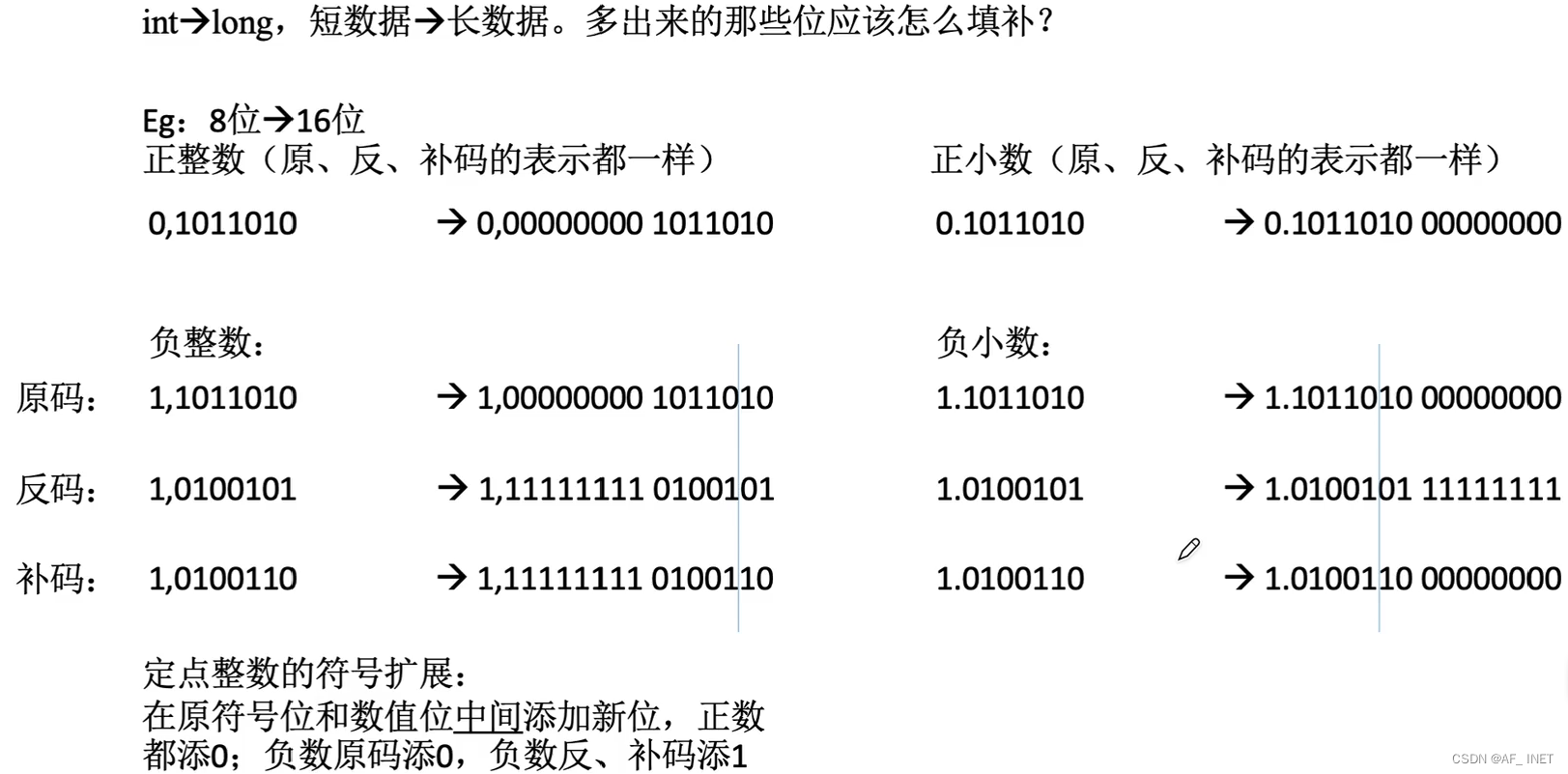

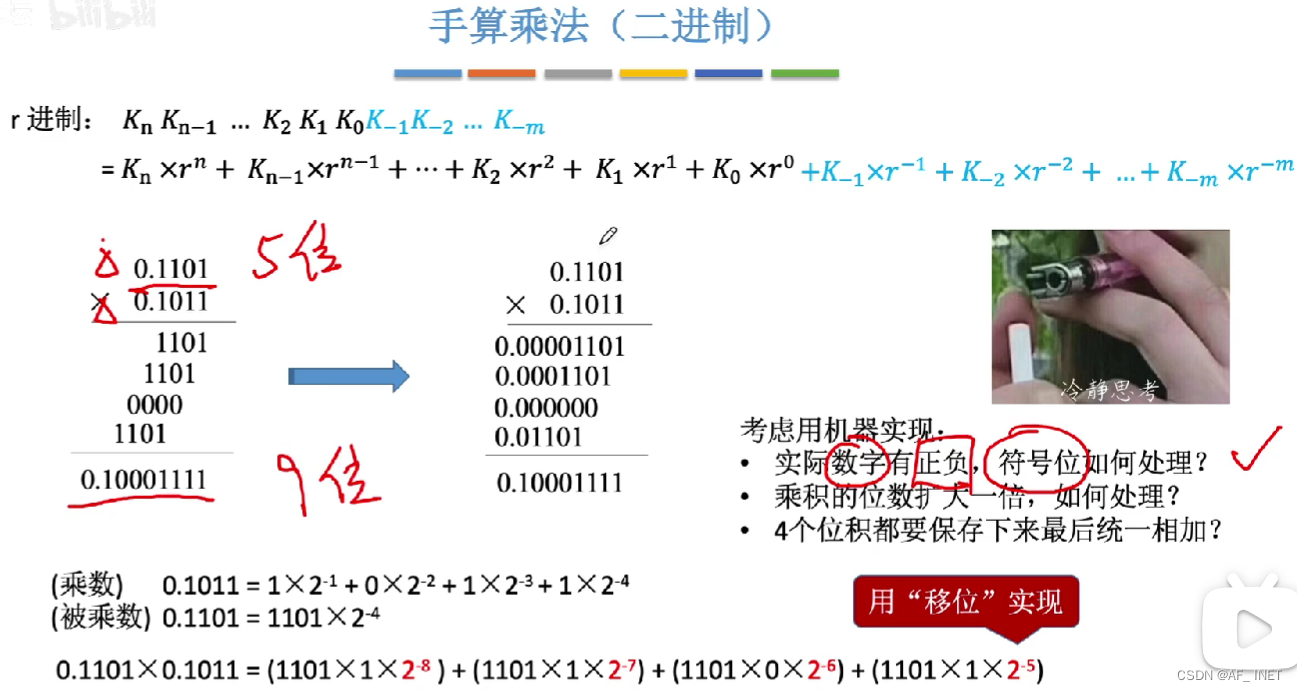
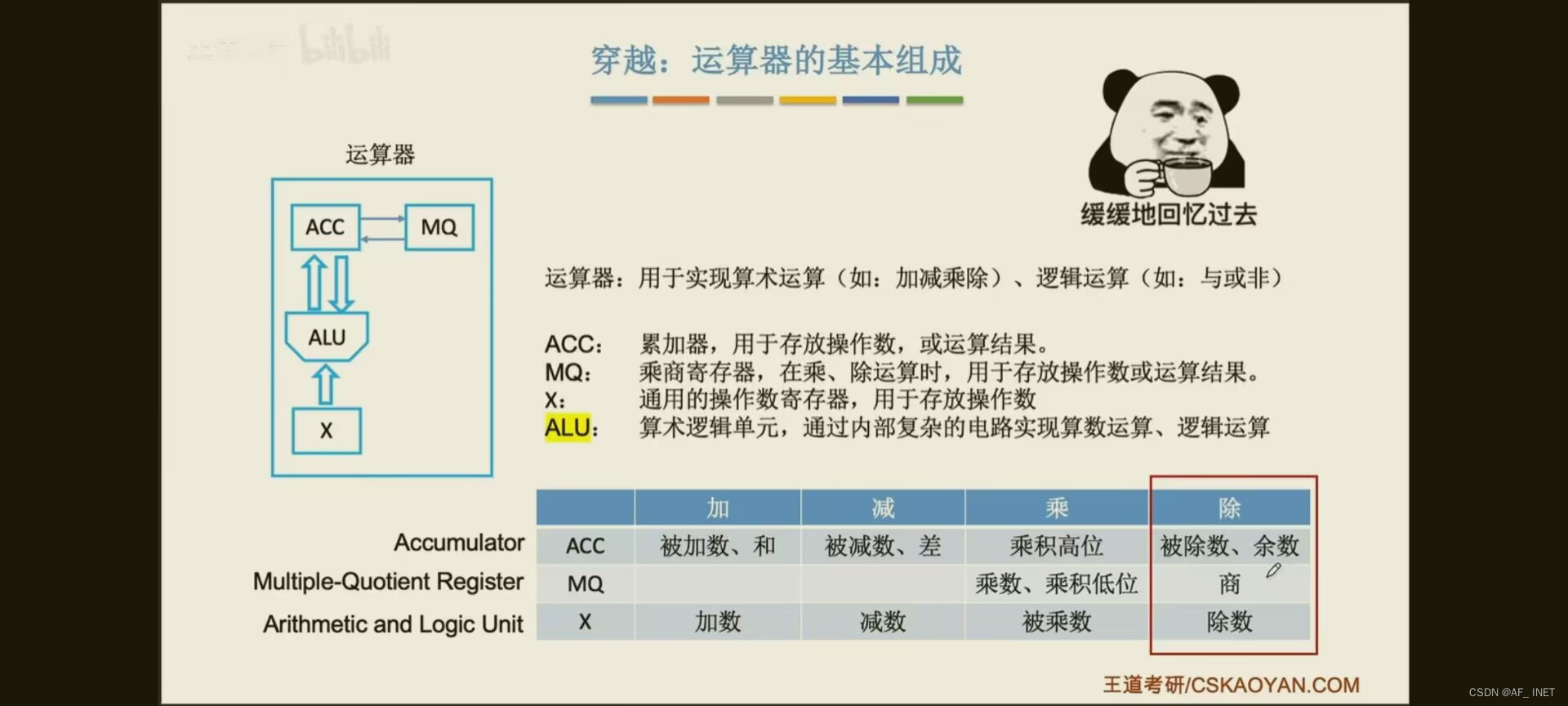
乘法运算
如何由机器实现乘法
1.符号位如何处理?
2.考虑寄存器可以保存的最大容量,不够怎么办?
3.乘出来得到的中间状态反别保存在单独的寄存器中?
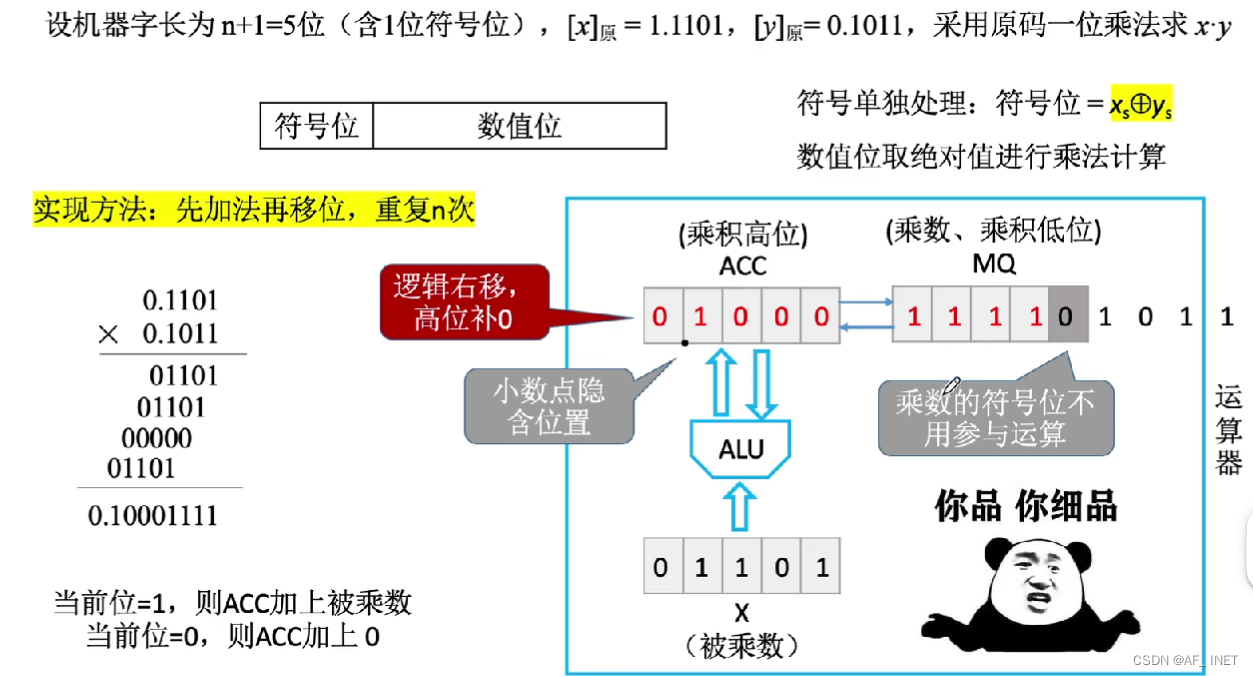
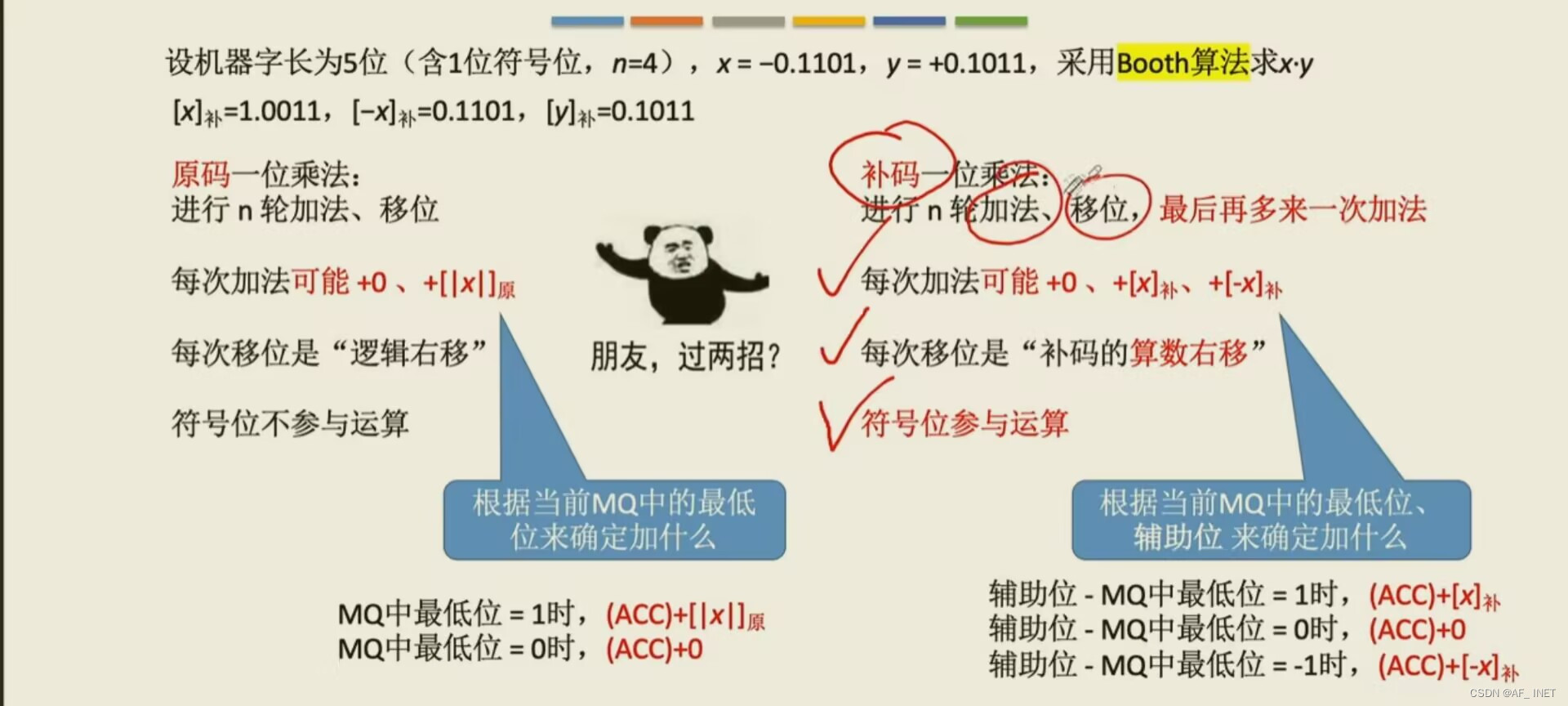
原码一位乘法:
1.如果乘数的当前位为1,则让ACC的值加上被乘数,如果当前位为0,则什么也不加,这个过程由算术逻辑单元ALU中的加法电路完成
2.乘数和ACC一起逻辑右移,ACC中的数进入了存储乘数的寄存器MQ,这样使得下一个位积和当前位积有了一个错位的相加,然后就是计算次低位和被乘数的位积

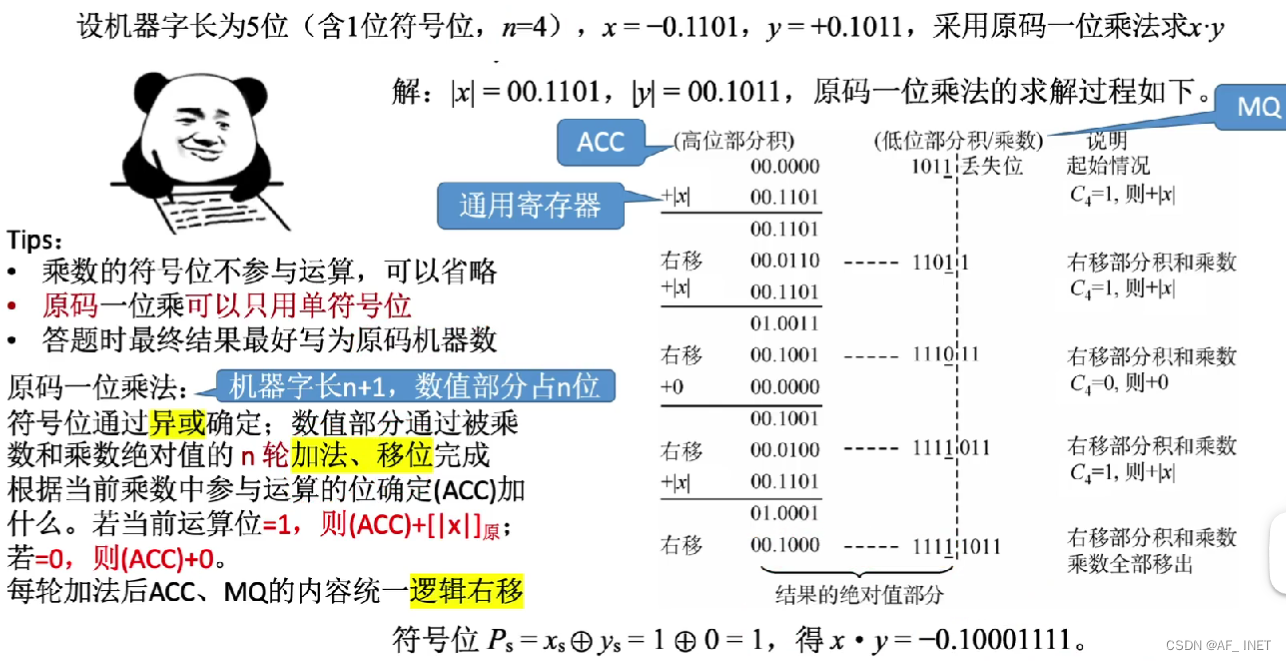
补码的乘法:
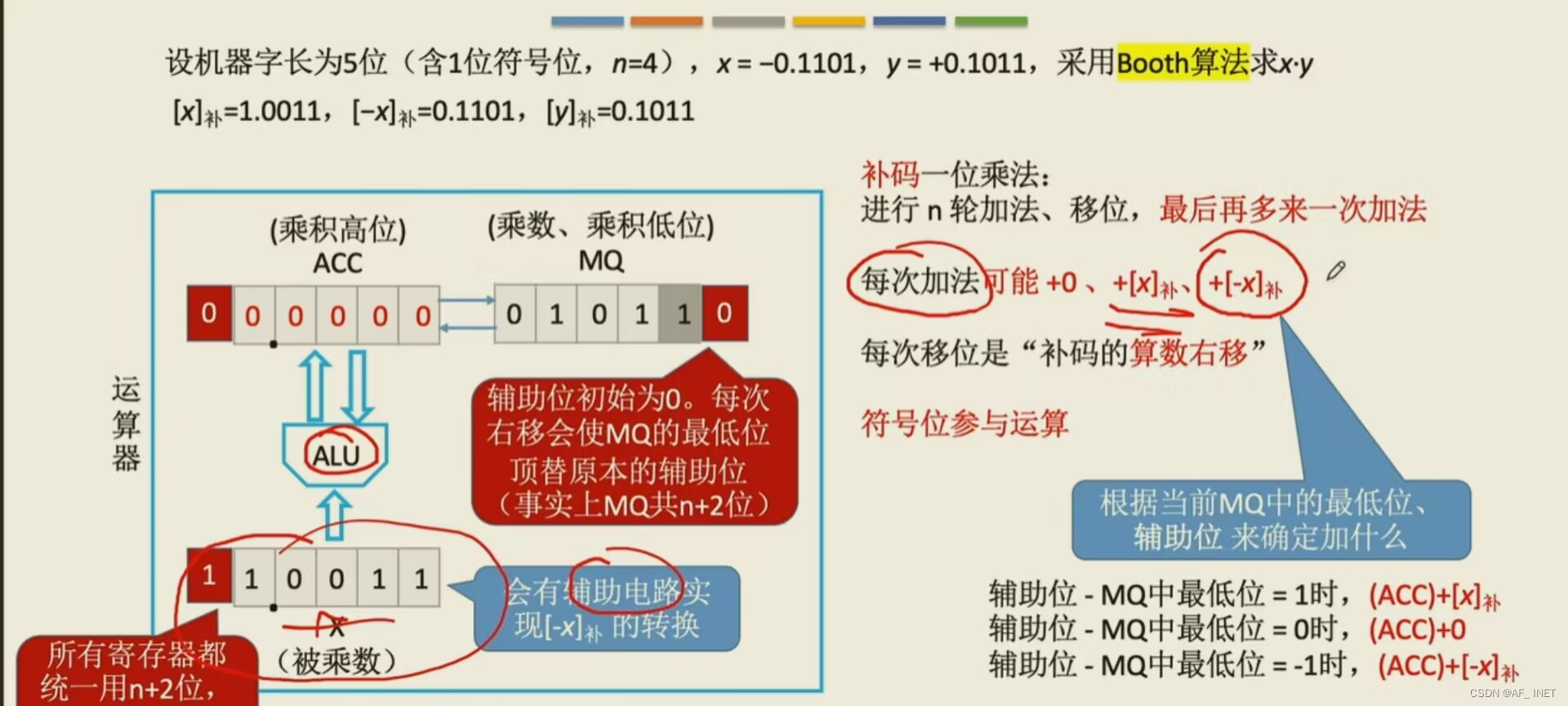


除法运算
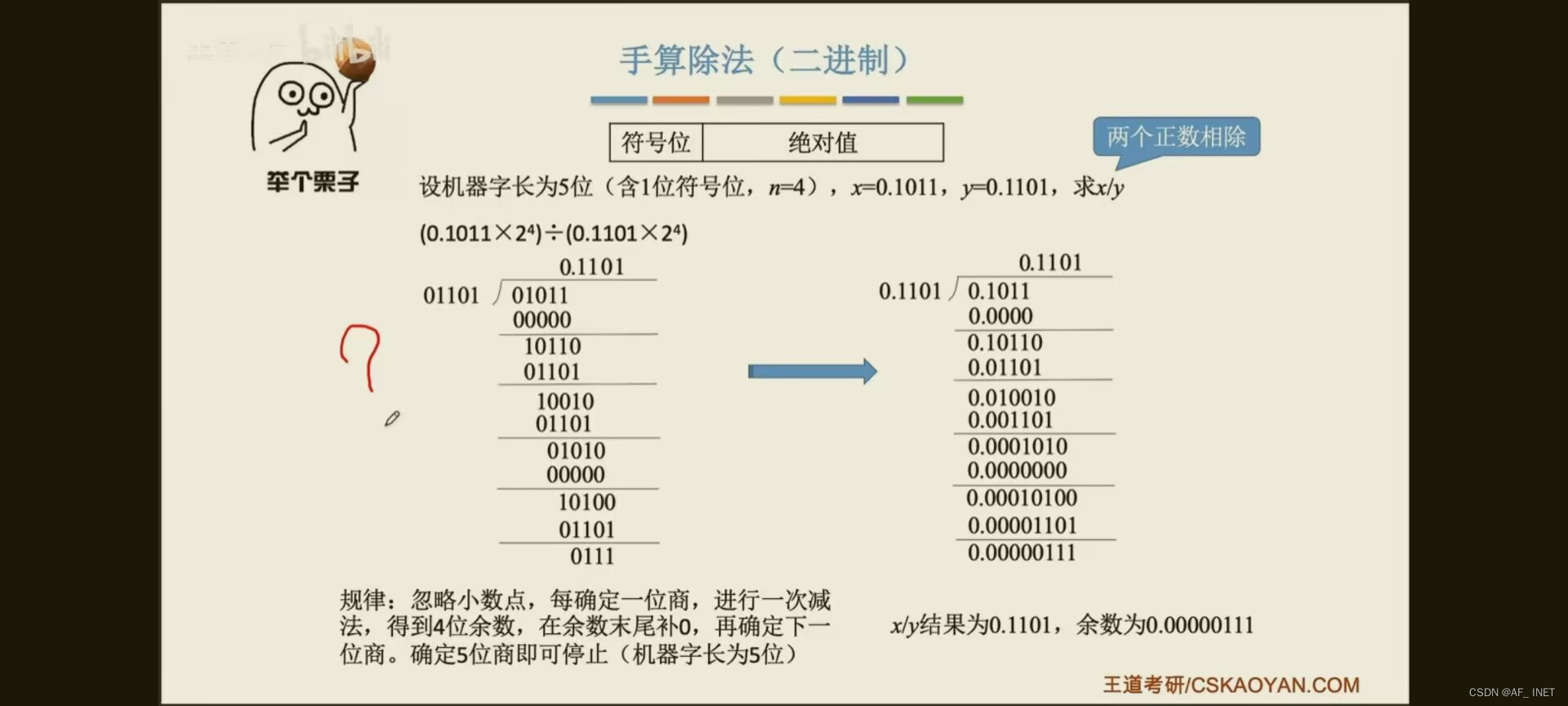
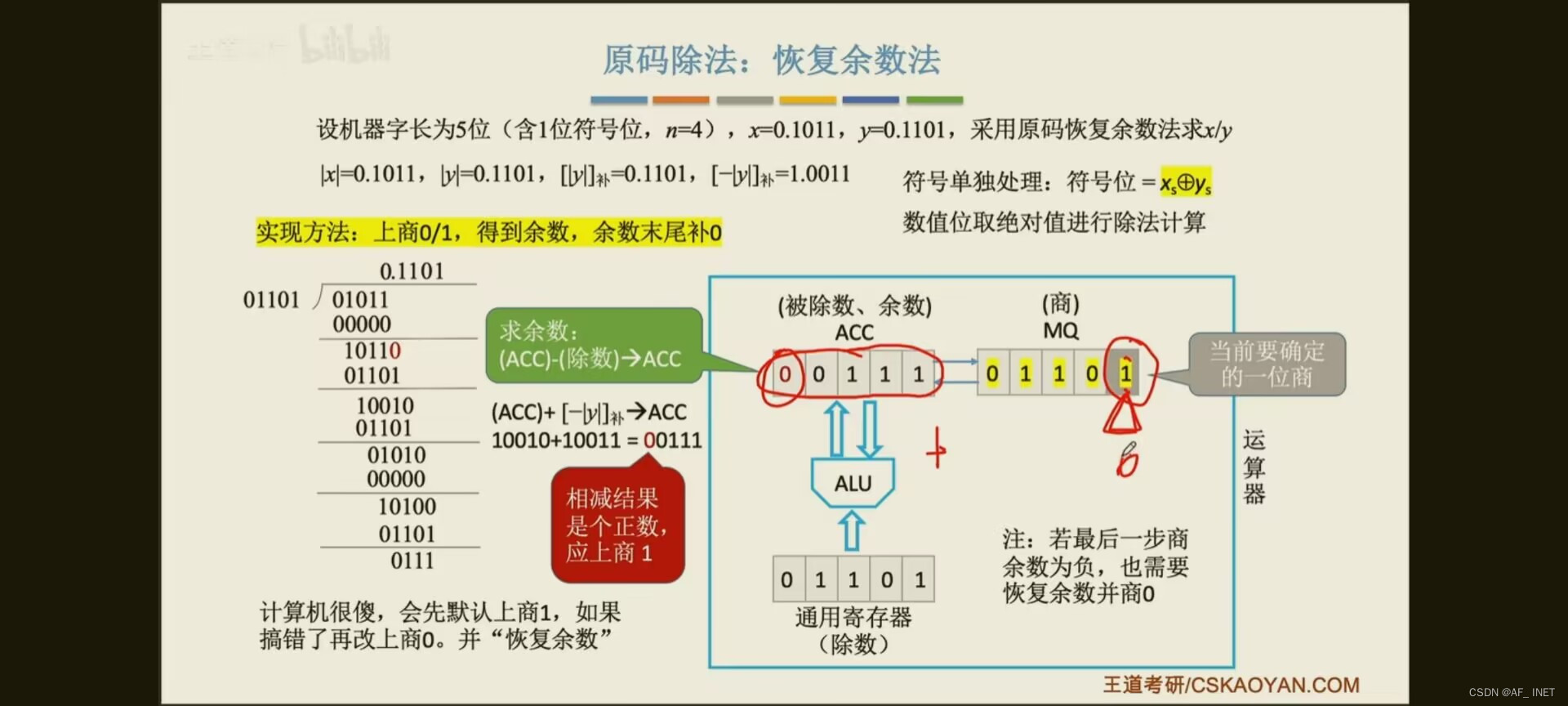
原码除法:恢复余数法

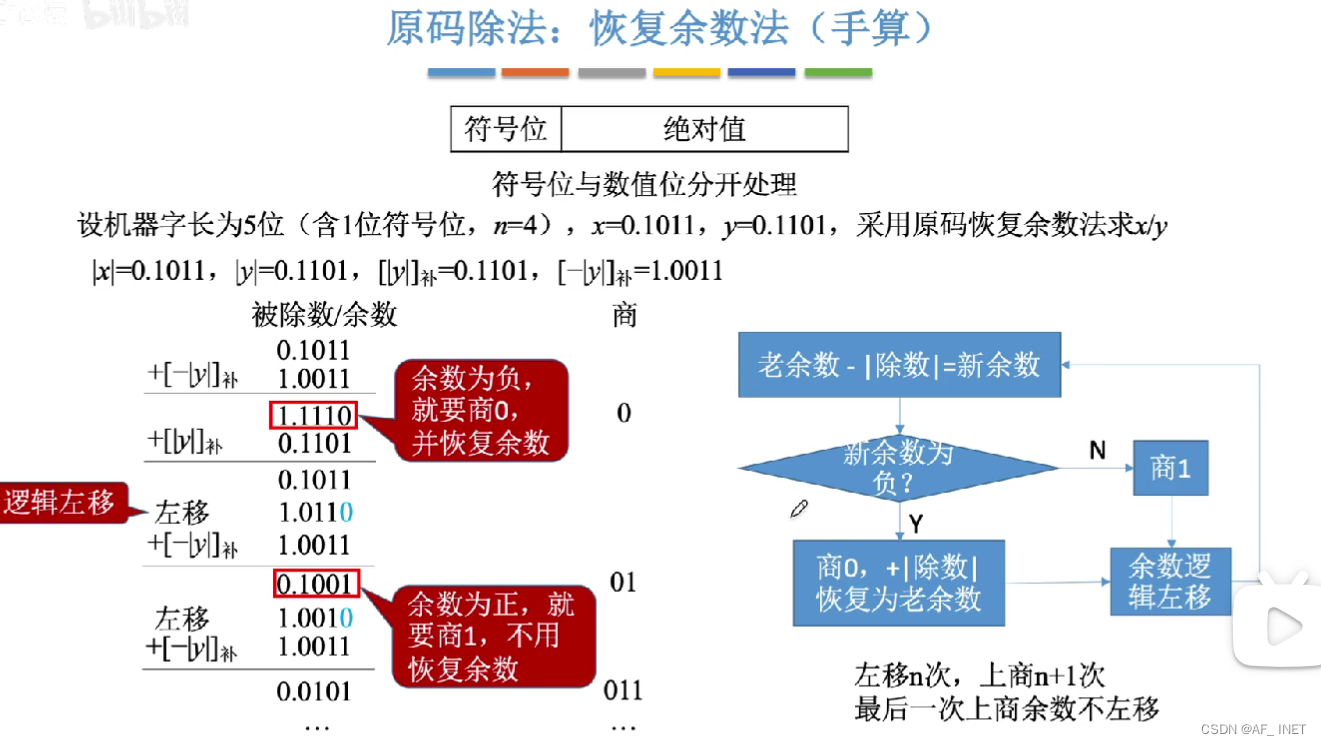
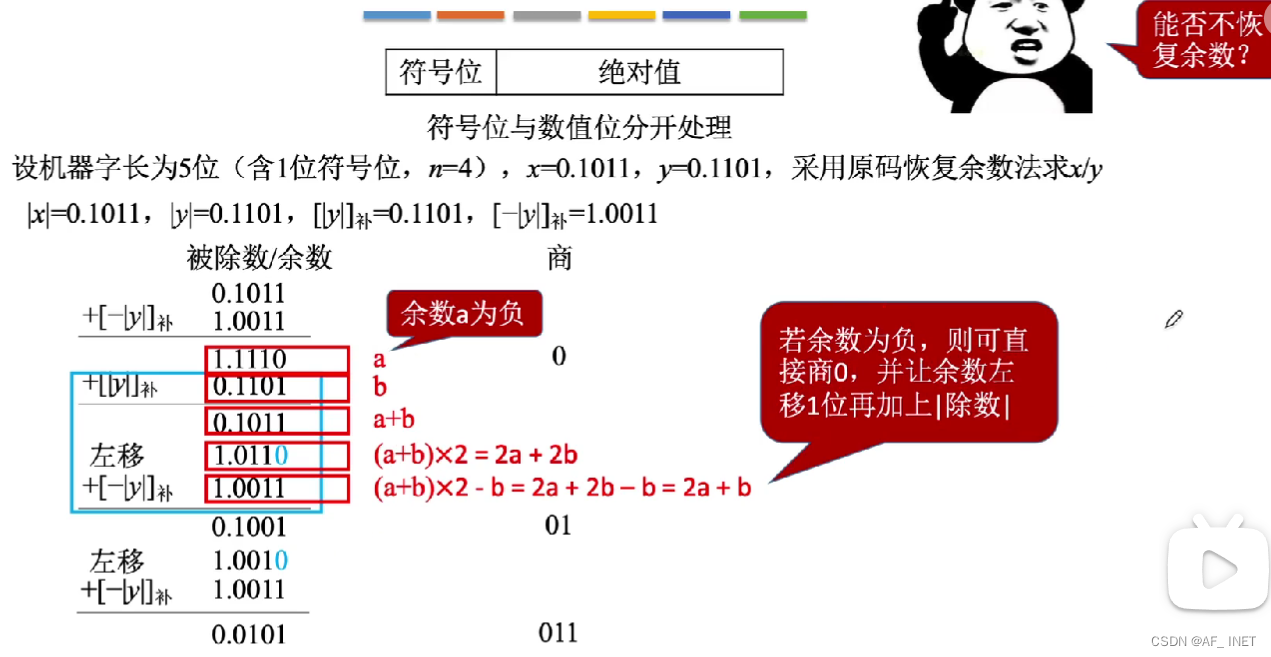
原码除法:加减交替法
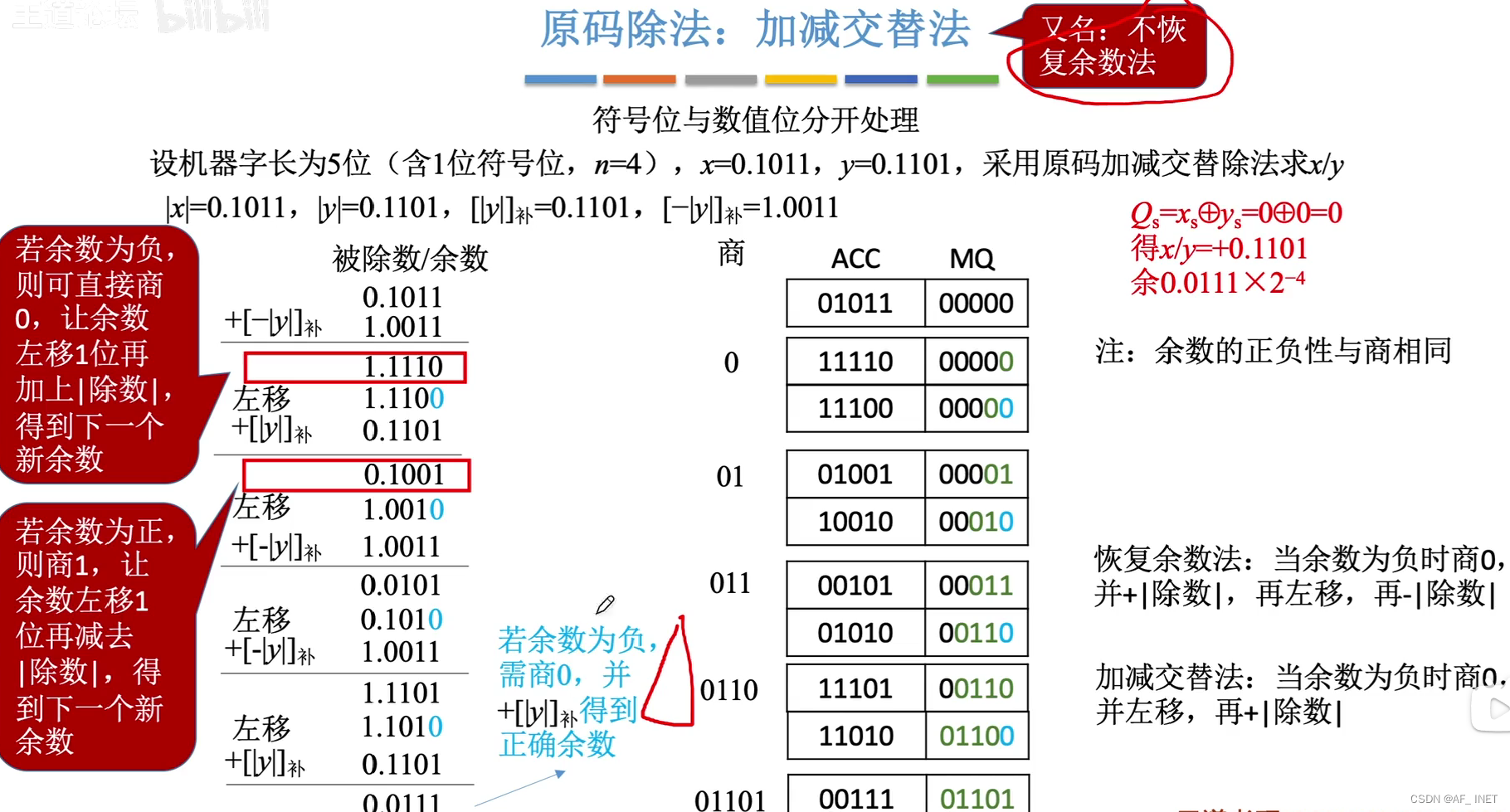
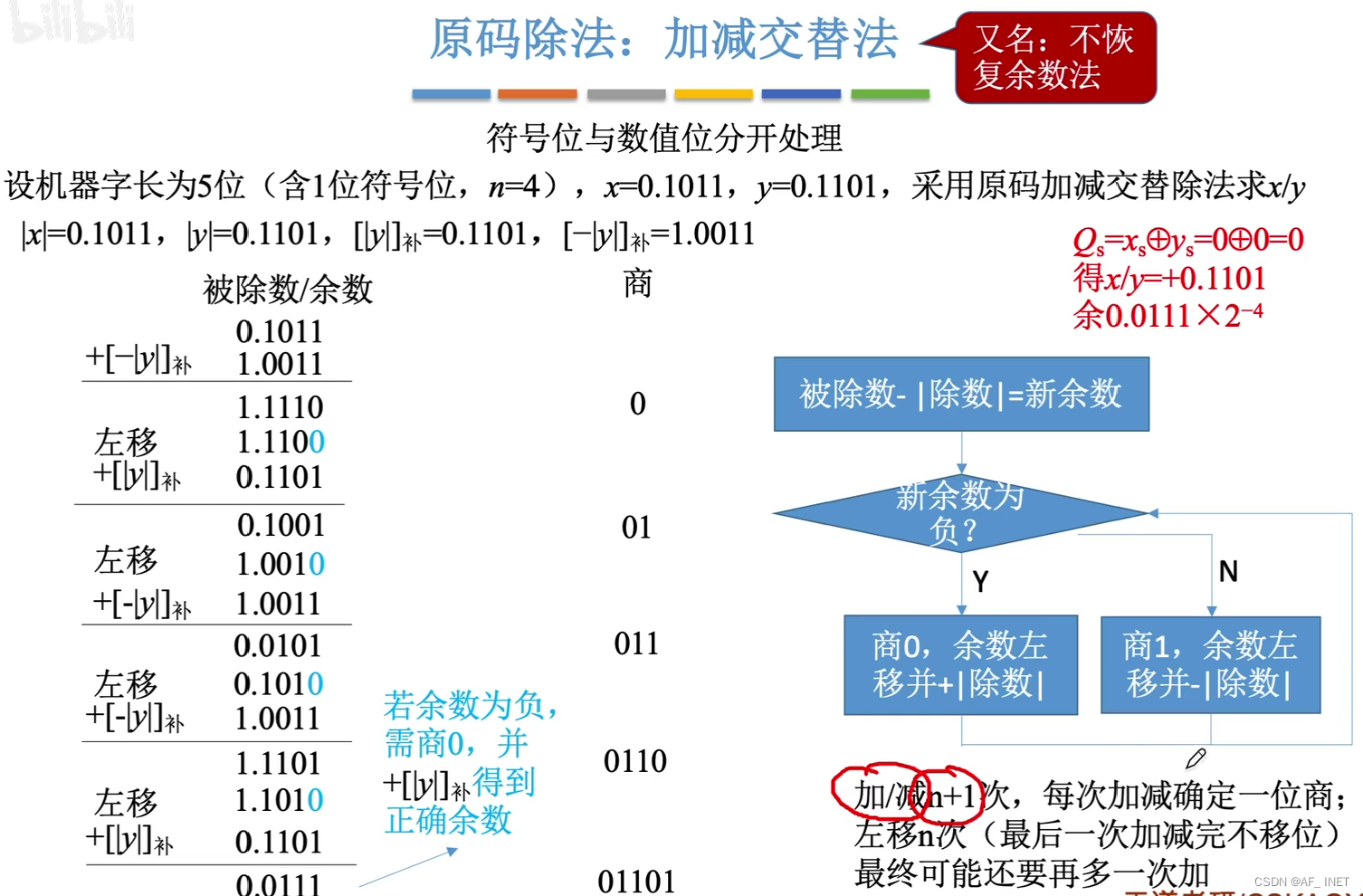
每进行一次加减就要更新一次余数,每更新一次余数就要根据余数的正负性确定一位商,最后一次可能还需要恢复余数,所以加减可能是n+2次
定点小数的除法运算,正常情况下第一步减去除数,一定要得到一个负值,如果第一步商1说明被除数比除数大,这种除法无法用定点小数表示,
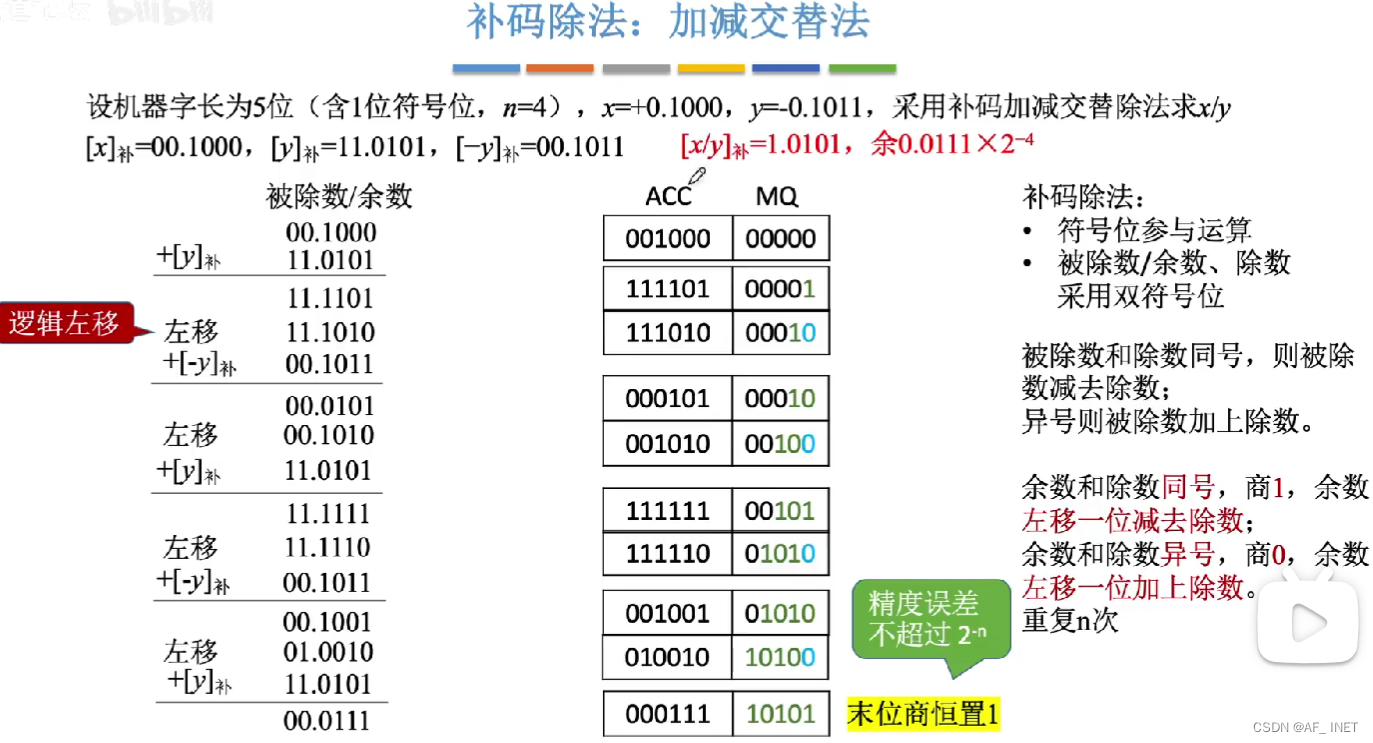
余数可能为正,可能为负,不需要修正,末位恒置为1保证精度并且
小结:

强制类型转换

数据的存储和排列:
1.大小端模式
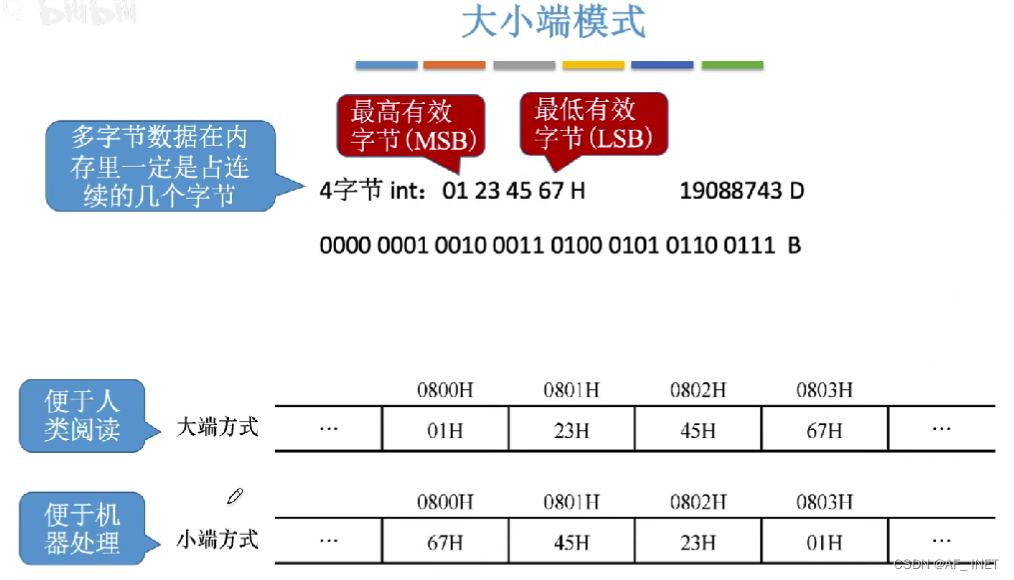
2.边界对齐
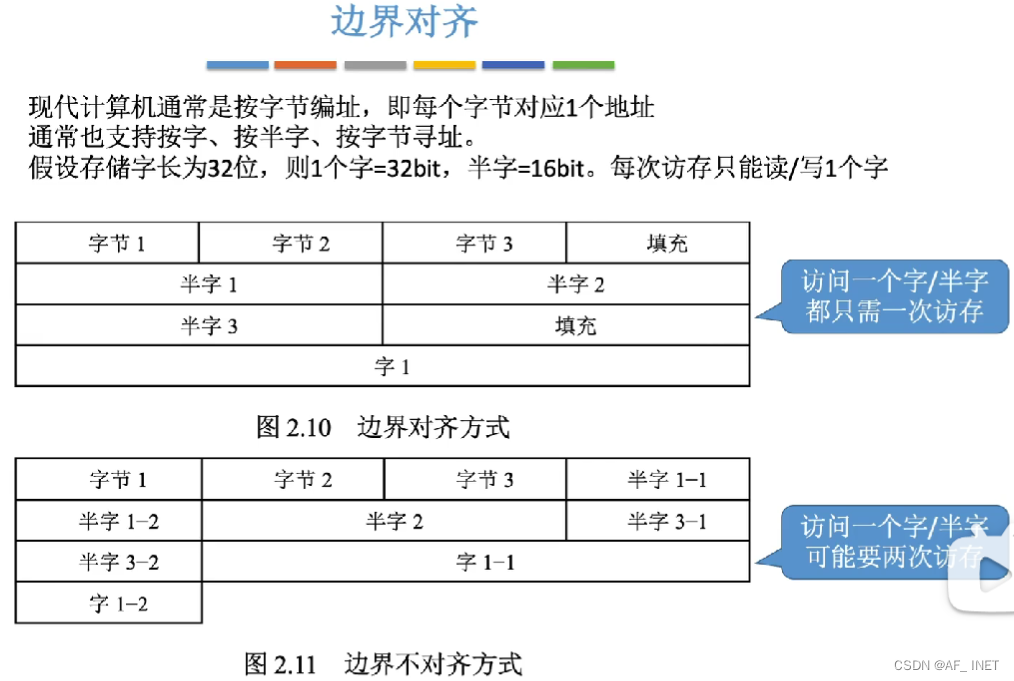
转换为字节地址:
字 ————> 半字 ————> 字节
逻辑左移一位 逻辑左移一位