目录
一.语言模型和序列生成
二.新序列采样
三.带有神经网络的梯度消失
四.GRU单元
一.语言模型和序列生成

上图的例子就是咱们的手机上的语音转文字输入差不多,说一句话,可能有多种可能的句子,那么到底是哪一种呢,咱们的语言模型就可以给出这些所有可能的句子的概率,最大概率的那个句子就是模型认为符合语音的那条句子。
术语:
corpus 语料库
语料库是自然语言处理的一个专有名词,就是很长的或者说数量众多的英文句子组成的文本。
构建语言模型:
像上篇文章讲的一样,假如你从训练集里得到一句话,那么我们需要先标记各个单词,然后我们为了能够区分出句子在哪里结尾,有时候可以给每个句子加一个结束标识符<EOS>。然后如果你想把标点符号也标记,那么你需要把标点符号也加入你的词典。然后就是上篇文章提到过的词典中没出现的词,标记为<UNK>。所以我们的模型不会对具体的哪个词典中没有的词建立概率模型,而是对<UNK>建立概率模型。

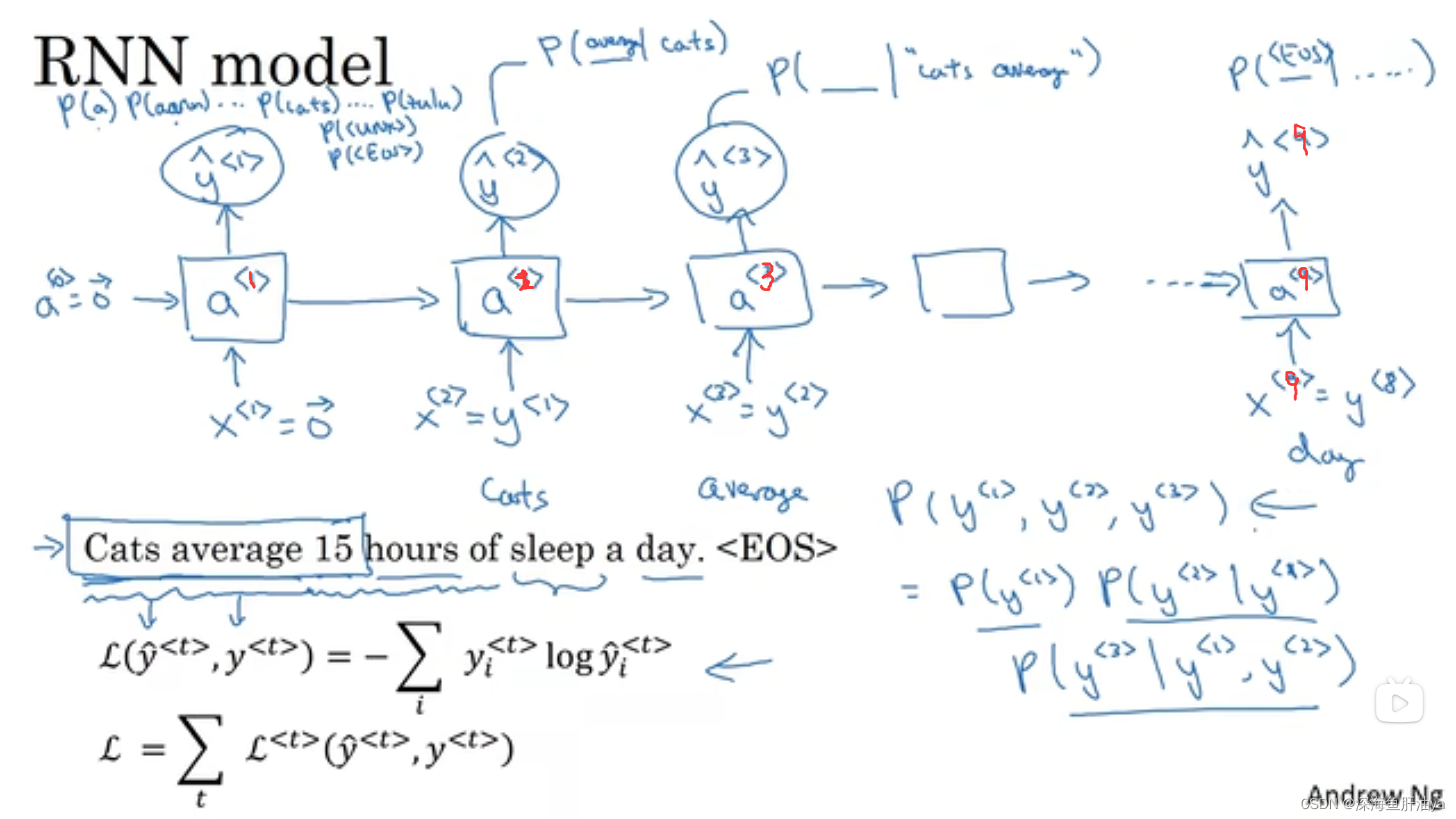
我们现在用RNN来训练一个自动生成文本的模型(有点像上节课讲的那个一对多模型,但是一对多是上一步的预测值当作下一步的喂入,而这里是用真实值喂入),如下图,假设我们最初输出入一个x^<1>是零向量,然后初始激活值a^<0>也设为零向量,模型计算出一个yhat^<1>(假设我们的词典有10000个词,然后我们的模型输出是经过了一个softmax,那么就有10000个分类,所以对应就有10000个概率,可能有10002个,因为我们可能还要加<UNK>和<EOS>标记),yhat^<1>就是最高概率对应的那个单词,然后第二个时间步时输入除了上一步的激活值,还有y^<1>(y^<1>就是真实序列的第一个单词,及训练集第i个训练示例的第一个元素,在本例中就是左下角那句话的第一个单词Cats),然后再计算y^<2>,y^<2>就是以前面的一个单词是Cats为前提条件的一个预测值,往后依此类推,可以看到这有点像概率论中的条件概率。
比如一个句子是由y^<1>,y^<2>,y^<3>组成的,则最终输出这个句子的概率就是三个条件概率相乘:

损失函数是下图右下角的式子
二.新序列采样
当你训练了一个模型想知道这个模型到底学到了什么,我们可以对新序列采样。
一个序列模型模拟了任意特定单词序列的概率,我们要做的就是对这个概率分布进行采样,
来生成一个新的单词序列。
让我们来看看具体怎么做:
来根据向量中这些概率的分布进行采样(词典中对应的每个单词的输出概率都不一样,所以抽样时不是等概率抽样),上半部分是已经训练好的模型,下面是我们调用模型生成新序列的过程,最开始给a^<0>和x^<1>都赋值为零向量,然后得到yhat^<1>,和上一节讲的一样,时间步最后经过softmax之后可能得到10002个值,所以我们随机取样是在这10002个值里取样(可以用np.random.choice函数来取样得到yhat^<1>),然后将yhat^<1>作为下一个时间步的输入之一(还有激活值a^<1>),以此类推,直到得到一个预测输出是<EOS>或者时间步数超出了咱们设定的最长时间步数才停止。
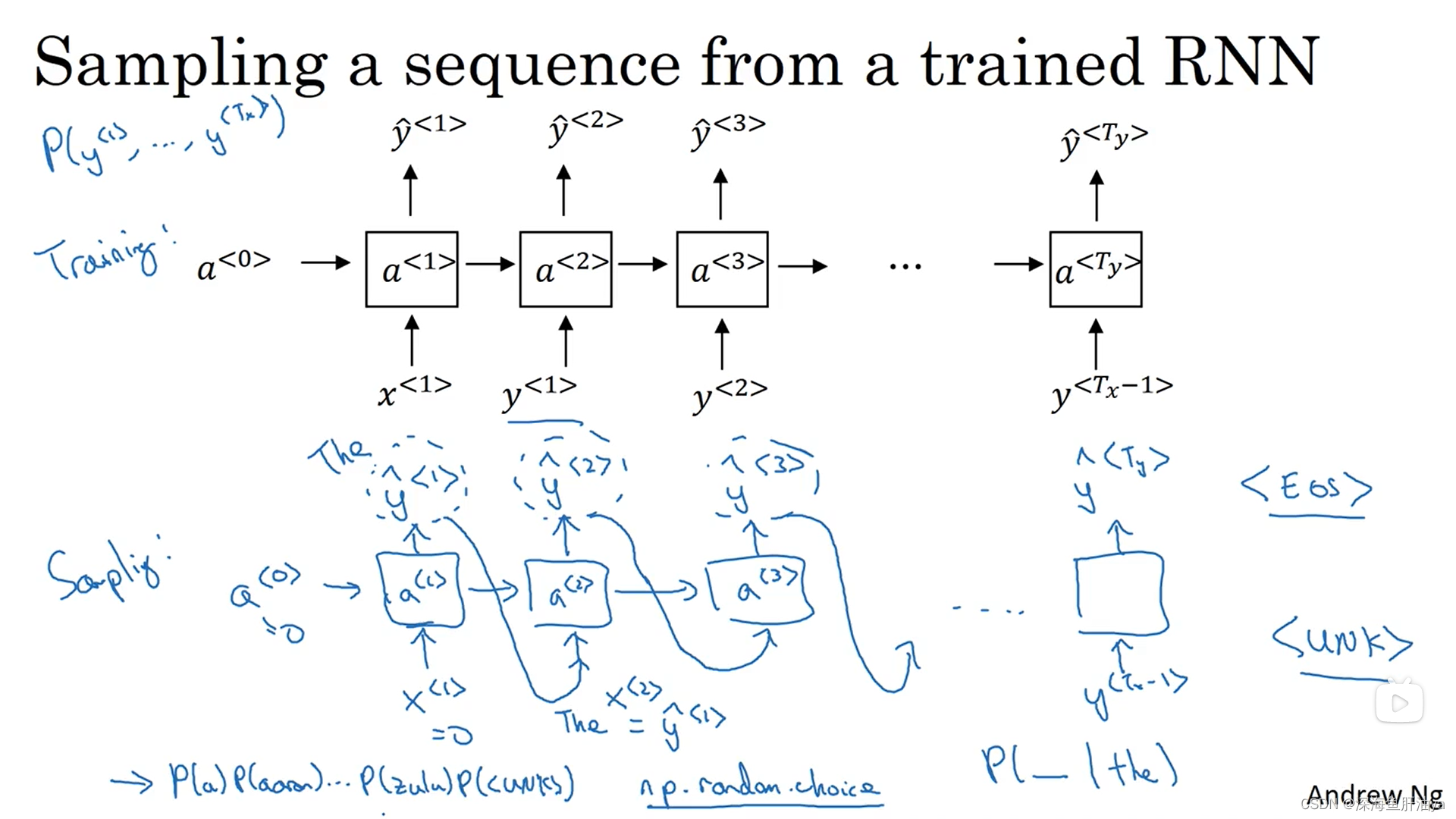
然后现在有一些方法不是基于单词来训练,而是基于字符,优点是不会收到<UNK>的困扰,缺点是计算昂贵等,现在应用得还不多,除非一些特定场景,比如很多专有词汇等场景。具体可以百度或看吴老师得视频课,我就不多说了。
三.带有神经网络的梯度消失
RNN不擅长处理长期依赖的关系,因为当网络层数很深的时候,就会容易遇到梯度爆炸和梯度消失的情况,对于RNN来说主要是梯度消失的问题(下面再详细说),梯度爆炸的话很容易被发现,因为梯度爆炸(比如RNN处理有1000个或者10000时间序列的数据集)会导致很多参数大到崩溃,比如参数值是NAN或者不是数字的情况,但是梯度爆炸比较好解决,但是梯度消失就比较棘手。
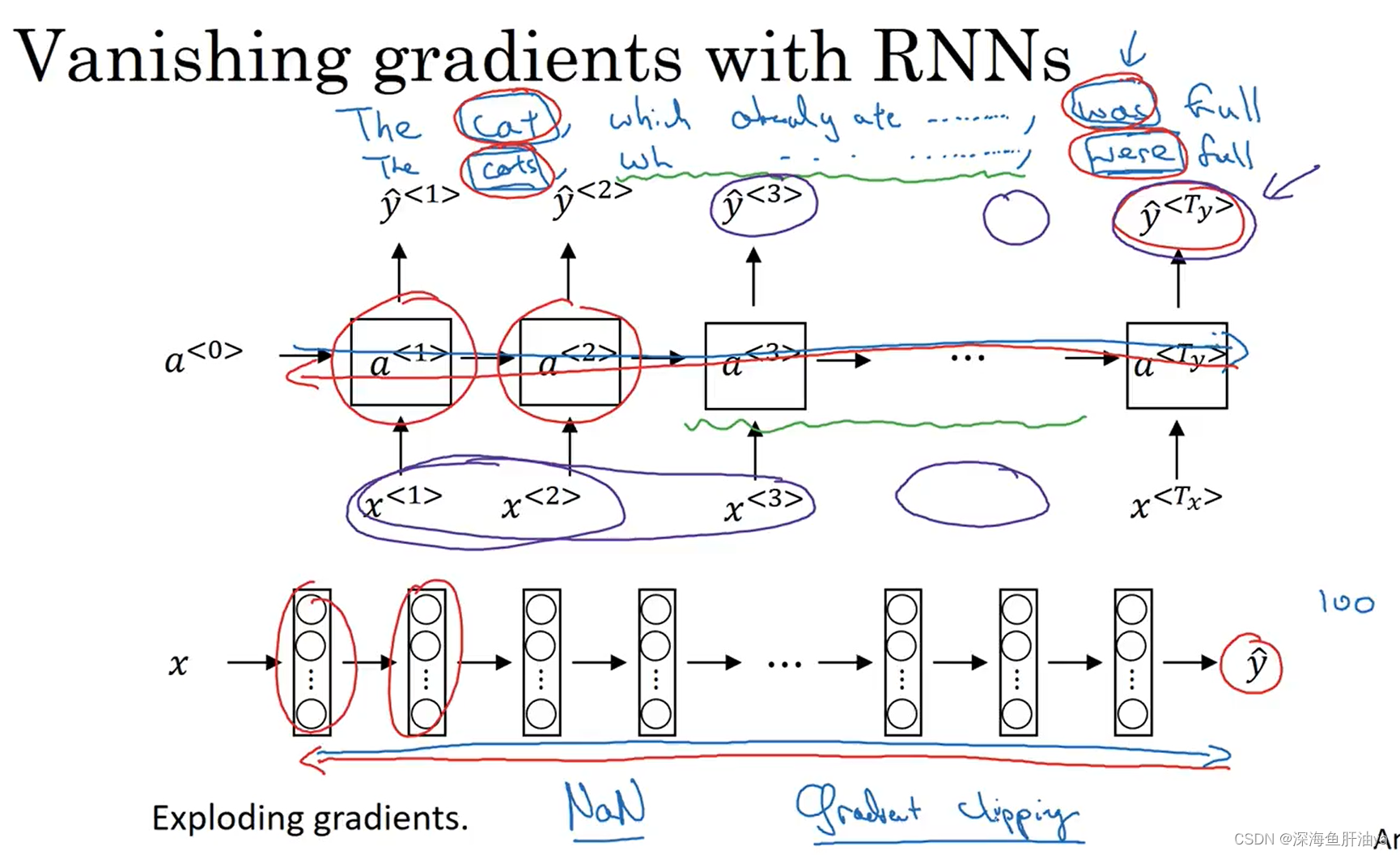
如上图,有两个很长的句子(这个猫吃了很多东西),上面的句子主语是cat,下面的句子主语是cats,然后句子末尾处使用一个be动词,如果是cat要用was,cats要用were。但是随着网络的加深,如果出现梯度消失,前面的层和后面的层越来越难以产生相互影响,比如输出yhat^<3>可能就受其附近的单元的输入(比如x^<1>,x^<2>,x^<3>)的影响。
四.GRU单元
GRU很好的解决了上述问题。
先来回看一眼RNN单元的结构 :
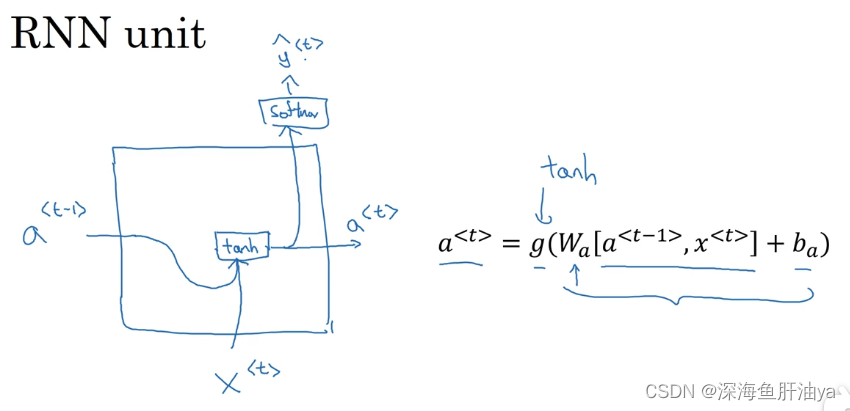
GRU这里的新符号:
c代表记忆单元(memory cell),于是在时间t处记忆细胞有关于t的值c,对于GRU来说,c^<t>=a^<t>,但是对于LSTM来说,c^<t>和a^<t>不是同一个东西。
那么c^<t>的作用是什么呢?
用我们上一节的那个例子说明一下就是从左往右遍历句子的时候记忆单元可以记住猫是单数还是复数,然后在后面要用到be动词的时候,可以通过记忆来判断是该用was还是were。
在每个时间步,我们将用一个候选值(c^~<t>)重写(更新)记忆单元(c^<t>)。
门(gamma_u)来决定是否要真的去更新记忆单元。
可以看到门是用sigmoid函数修饰的,所以门的输出大部分都很接近于1或0。可以看到右下角的式子,当门接近于0时,那么c^<t>=c^<t-1>(不更新),当门接近于1时,c^<t>=c^~<t> (更新)。
然后现在看到左下角的那句文本,遇见cat时,比如单数时让c^<t>=1,然后再往后的一串单词对应的门都是接近于0,也就是不更新,这样就保留了记忆单元的值,这样即便cat/cats和was/were隔得很远,也不会因为距离的变远而发生梯度消失的问题。当下次主语改变时,可能门的值也就改变了,随着而来的就是记忆单元的值也会发生改变。

下面是一个更加完整的GRU单元,可以看到又新增了一个门gamma_r,除了gamma_r的式子,c^~<t>也做了改动,gamma_r代表着c^~<t>和c^<t-1>的关联性。在其他学术文章中,可能会用其他符号(左侧那四个)。
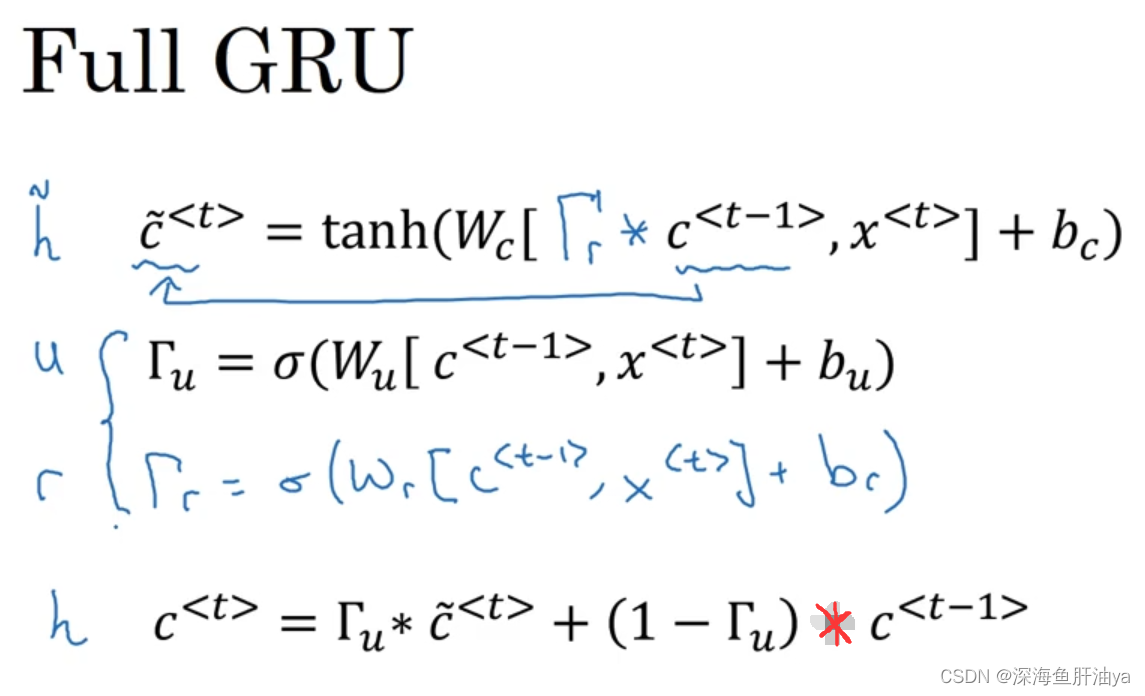



![[glacierctf 2022] 只会3个](https://img-blog.csdnimg.cn/28f8e956b66042c490a77ab0fd46c28d.jpeg)