线段树 之 延迟数组

1. 前言

线段树是一类特殊的完全二叉树，其本质是对递归过程信息的再处理和再记忆，线段树构造完成后，可以脱离原始数组或线性表，直接对线段树进行查询或更新操作即可。线段树的储存结构和堆结构类似，如果父节点的下标为v,那么左孩子节点的下标可以表示为2*v, 右孩子节点的下标可以表示为2*v+1，依此类推。

2. 延迟数组定义

延迟数组采取的是空间换取时间的策略，在递归遍历线段树过程中，在某些时候只需要对局部区间进行相关更新/查询，而不需要深入到底层进行更新/查询，在后续需要的时候再继续更新操作。那么这就带来一个问题，后续操作中，如何判断是否需要额外更新呢？ 这就需要定义延迟数组，延迟数组可以选择布尔类型，也可以选择其它数据类型，它的作用是在后续的更新或查询操作时候，把信息提前传递给双子节点，在需要采集信息之前，对双子节点的信息进行相关的更新/查询。

延迟数组可以降低递归的深度，提前结束递归，比如我们游览大型公园，对于有些景点，由于时间关系，不能深入景点参观，可以在入口处标记“到此一游，下面景点需要门票5元”，藉此提醒，下次再踏入后续景点前，直接买好门票游览即可。

延迟数组在更新线段树的时候，如果查询到某个区间满足更新要求，那么它直接更新此区间的值，同时对此区间上的延迟数组的值进行相应的更新即可，而无需更新其子孩子。

3. 延迟数组应用

首先我们建立一个区间最大值的线段树，然后更新操作对区间[l,r]范围内的所有元素加上某个常数addend, 更新操作完成后， 再查询某个区间内的最大值。

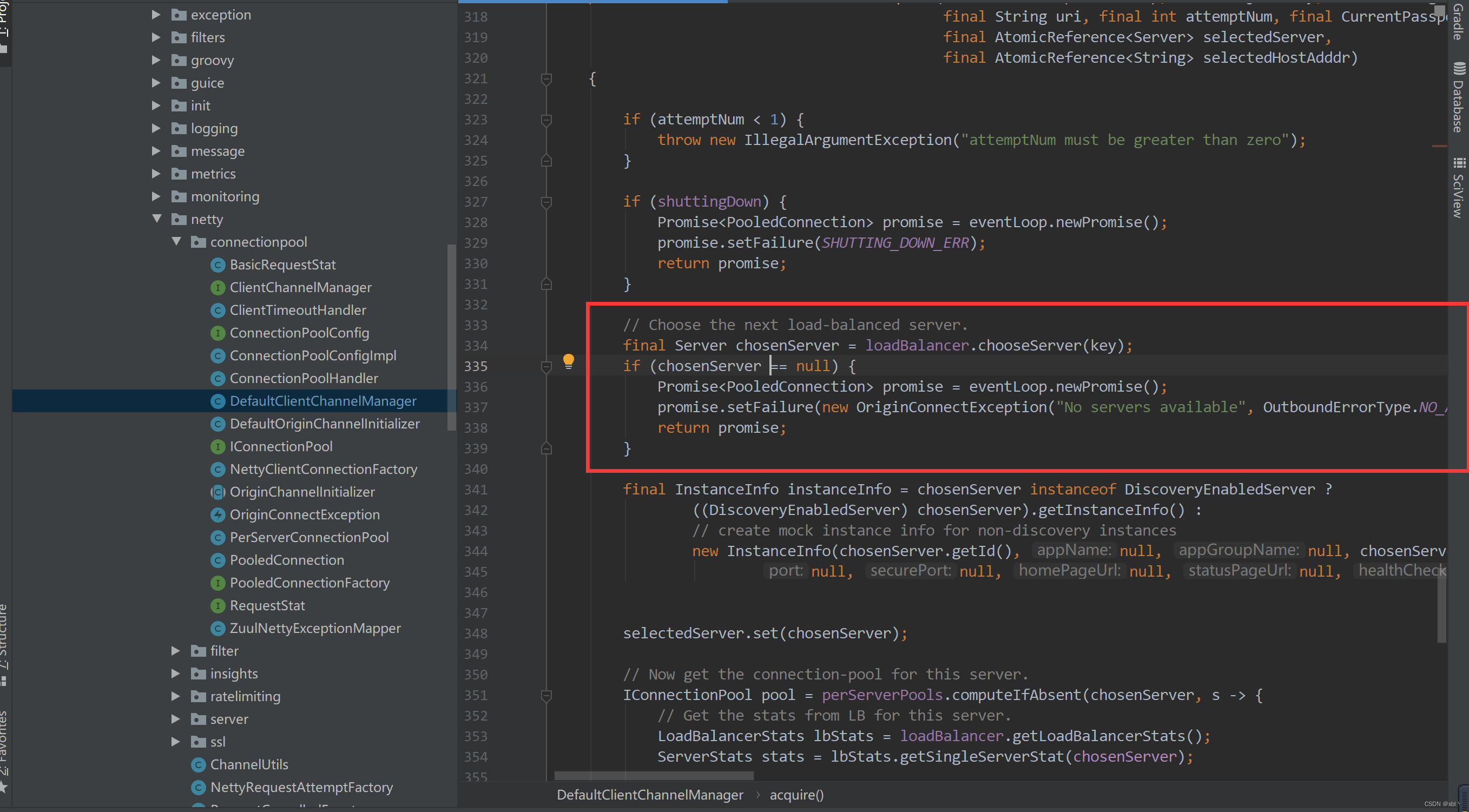
用一个具体例子来说明，已知数组a[0…4]={1, 3, 16, 8, 6}, 根据数组建立区间最大值线段树，线段树为二叉树结构，表示为，

要求在区间a[2…4]所有的元素都加上10，并定义lazy[]数组跟踪相关情况。在更新过程中，由于有lazy数组进行标记，

整个过程中，只需要更新a[2…2], a[0…2], a[3…4]和a[0…4]，注意观察，过程中并没有更新a[3…3]和a[4…4]，这一步就是lazy[]数组发挥作用的地方，如果二叉树深度很大，那么就可以节省大量的遍历时间。

接下来我们回到查询最大值的过程，假设要求查询a[4…4]区间上的最大值，在查询过程中，遍历过程可以表示为，

先遍历a[0…2]返回-∞，然后来到a[3…4]，此时需要调用push函数，把父节点的lazy数组当中的信息和操作传递给子节点，操作之后a[3…3]更新为18，a[4…4]更新为16；由于a[3…3]不满足边界条件，所以返回-∞，a[4…4]返回16（更新后的值），然后回退，比较max(-∞，16)得到16，然后再比较max(-∞,16)得到最终的返回值16，也就是a[4…4]区间上的最大值。

4. 代码实现

建立线段树的实现，之前文章已经阐述，终点关注3个函数push函数，update函数和更新后的query函数。

push函数的作用是在更新和查询之前，把父节点里面的信息/指令操作传递给子节点，并在子节点上进行相关的操作，操作完成后，父节点的lazy数组复原。

update函数的道理也类似，在进行递归之前，需要先调用push函数，对子节点的信息进行更新，然后再往下进行。

对于 query函数，道理相同。

第一部分，头文件定义：

/**
 * @file Lazy_query.h
 * @author your name (you@domain.com)
 * @brief 
 * @version 0.1
 * @date 2023-04-10
 * 
 * @copyright Copyright (c) 2023
 * 
 */

#ifndef LAZY_QUERY_H
#define LAZY_QUERY_H
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <limits.h>
#define MAXN 10

int t[4*MAXN]; // t will be segment tree array

int lazy[4*MAXN]={0};

/**
 * @brief Build segment tree based on segment array and original array
 * 
 * @param nums Original array to provide the number
 * @param v Segement array index(2*v, 2*v+1)
 * @param tl Total left boundary
 * @param tr  Total right boundary
 */
void build(int *nums,int v,int tl, int tr);




void push(int v);

int query_lazy(int v, int tl, int tr, int l, int r);


/**
 * @brief Add addend to the range from l to r
 * 
 * @param v Segement tree index
 * @param tl Total left boundary
 * @param tr Total right boundary
 * @param l  To be searched left side
 * @param r  To be searched right side
 * @param addend To be added with the number of addend
 */
void update_lazy(int v, int tl, int tr, int l, int r, int addend);


int min(int a, int b);


int max(int a, int b);

#endif

第二部分，基本函数的实现，

/**
 * @file lazy_query.c
 * @author your name (you@domain.com)
 * @brief 
 * @version 0.1
 * @date 2023-04-10
 * 
 * @copyright Copyright (c) 2023
 * 
 */

#ifndef LAZY_QUERY_C
#define LAZY_QUERY_C
#include "lazy_query.h"

void build(int *nums, int v, int tl, int tr)
{
    int tm;

    if(tl==tr)
    {
        t[v]=nums[tl]; //exit entry for the recursion
    }
    else
    {
        tm=(tl+tr)/2; //divide the segement t[] into two parts
        build(nums,2*v,tl,tm); //2*v represents the left part of the segment tree
        build(nums,2*v+1,tm+1,tr); //2*v+1 represents the right part of the segment tree
        t[v]=max(t[2*v],t[2*v+1]); //post-order traversal, 左右中，左边值和右边值已经求出
    }

    return;
}


void push(int v)
{
    t[2*v]+=lazy[v];
    t[2*v+1]+=lazy[v];// add lazy[v] to the next level

    lazy[2*v]+=lazy[v];
    lazy[2*v+1]+=lazy[v]; //pass down to the next level

    lazy[v]=0; //return to original point
}

int query_lazy(int v, int tl, int tr, int l, int r)
{
    int tm;
    int left_side;
    int right_side;
    int max_value;

    if(l>r)
    {
        return INT_MIN;
    }
    else if(tl==l && tr==r)
    {
        return t[v];
    }
    else
    {
        push(v); // update its decedent children
        tm=(tl+tr)/2;

        left_side=query_lazy(2*v,tl,tm,l,min(r,tm));
        right_side=query_lazy(2*v+1,tm+1,tr,max(l,tm+1),r);

        max_value=max(left_side,right_side);

        return max_value;
    }
}

void update_lazy(int v, int tl, int tr, int l, int r, int addend)
{
    int tm;
    if(l>r)
    {
        return; // no action with any value updated
    }

    if(tl==l && tr==r)
    {
        t[v]=t[v]+addend;
        lazy[v]+=addend; // in the range, lazy[v] hadd been updated
    }
    else
    {
        push(v);
        tm=(tl+tr)/2;

        update_lazy(2*v,tl,tm,l,min(r,tm),addend);
        update_lazy(2*v+1,tm+1,tr,max(l,tm+1),r,addend);

        t[v]=max(t[2*v],t[2*v+1]);
    }

    return;

}

int min(int a, int b)
{
    return (a<b?a:b);
}

int max(int a, int b)
{
    return(a>b?a:b);
}

#endif

第三部分，测试函数

/**
 * @file lazy_query_main.c
 * @author your name (you@domain.com)
 * @brief 
 * @version 0.1
 * @date 2023-04-10
 * 
 * @copyright Copyright (c) 2023
 * 
 */
#ifndef LAZY_QUERY_MAIN_C
#define LAZY_QUERY_MAIN_C
#include "lazy_query.c"

int main(void)
{
    int nums[]={1, 3, 16, 8, 6};
    int nums_size=sizeof(nums)/sizeof(int);

    int tl;
    int tr;
    int l;
    int r;
    int pos;
    int max_value;
    int addend;

    tl=0;
    tr=nums_size-1;
    l=2;
    r=4;
    addend=10;

    pos=1;
   

    build(nums,1,tl,tr);
    update_lazy(1,tl,tr,l,r,addend);
    max_value=query_lazy(1,tl,tr,4,4);

    getchar();

    return EXIT_SUCCESS;
}


#endif

5. 小结

本文对延迟数组的应用做了简单分析，延迟数组核心思想是“60分万岁，一分不多，一分不少“，每一步都严格按照需求做到最小化的更新或查询，尽可能减少更新或查询的时间，做到程序的时间复杂度最低；代价是需要定义一个和线段树同维度的lazy数组，对每一步的信息进行记录，以便后续把父节点的信息及时传递给子节点。

参考资料：

Segment Tree - Algorithms for Competitive Programming (cp-algorithms.com)