氢原子的电子轨道半径、能量、速度

news2024/11/9 0:47:37

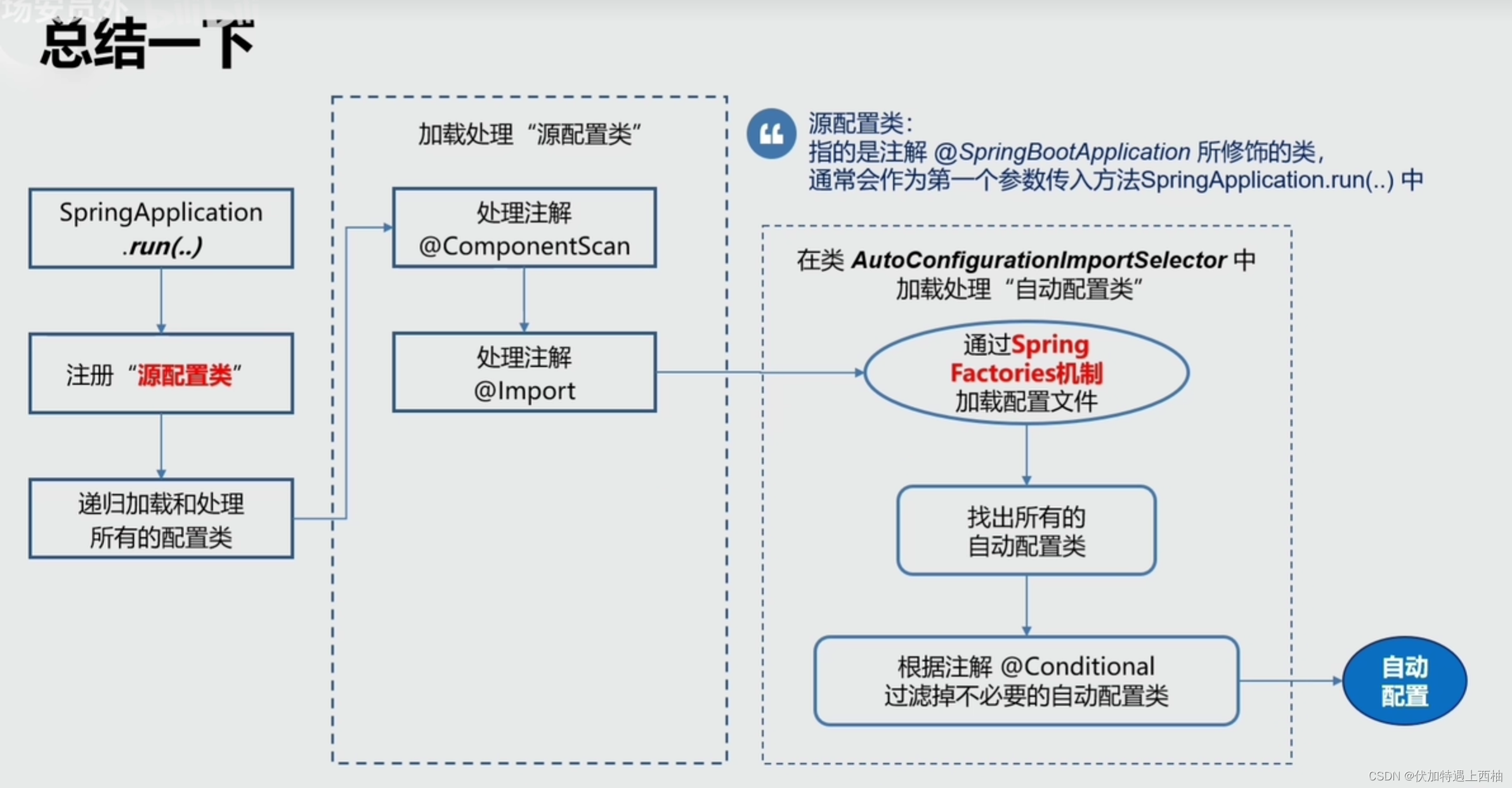
在https://blog.csdn.net/qq_35379989/article/details/130065868?spm=1001.2014.3001.5501中我们已经给出了波尔模型的三大假设：定态假设、跃迁假设以及角动量量子化。

一、氢原子的轨道半径

在跃迁假设中，通过设定波尔模型轨道能量： $E_n=-\frac{R_H h c}{n^2}$ 与电子动能和势能能量公式： $E=T+V=\frac{1}{2} m_e v^2-\frac{1}{4 \pi \varepsilon_0} \cdot \frac{Z e^2}{r}=-\frac{1}{2} \frac{1}{4 \pi \varepsilon_0} \cdot \frac{Z e^2}{r}$ 联立，可以得到电子的轨道半径为： $r_n=\frac{1}{4 \pi \varepsilon_0} \frac{e^2}{2 R_H h c} n^2$ 。

在上方，已经给出了电子轨道半径为： $r_n=\frac{1}{4 \pi \varepsilon_0} \frac{e^2}{2 R_H h c} n^2$ ，结合 $R_H=\frac{2 \pi^2 e^4 m_e}{\left(4 \pi \varepsilon_0\right)^2 \cdot c h^3}$

令： $a_0=\frac{4 \pi \varepsilon_0 h^2}{4 \pi^2 m e^2}=0.53 \times 10^{-10} \mathrm{~m}$

则可以获得氢原子量子化的轨道半径为： $r_n=a_0 n^2$ （其中,n为氢原子的线系/主量子数，n=1为莱曼系，n=2为巴尔末系，...）

当n=1时，我们称其为氢原子的第一波尔半径，简称为波尔半径。

二、氢原子能量

氢原子电子轨道能量为： $E_n=-\frac{R_H h c}{n^2}$ ，且里德伯常数有公式： $R_H=\frac{2 \pi^2 e^4 m_e}{\left(4 \pi \varepsilon_0\right)^2 \cdot c h^3}$ ，带入后可得：

$E_n=-\frac{2 \pi^2 e^4 m_e}{\left(4 \pi \varepsilon_0\right)^2 \cdot h^2} \frac{1}{n^2}=-\frac{m_e c^2}{2}\left(\frac{e^2}{4 \pi \varepsilon_0 \hbar c}\right)^2 \frac{1}{n^2}$

其中，将 $\frac{e^2}{4 \pi \varepsilon_0 \hbar c}$ 定义为 $\alpha$ ，其值近似为： $\alpha \approx \frac{1}{137}$ （1/137为一个神奇的无量纲常数，可以再电动力学、量子力学和相对论中看到它）。

将已知常数带入，可以进一步得到，氢原子的能量表达式为：

$E_n=-13.6 \frac{1}{n^2}(\mathrm{eV})$

当n=1时为氢原子的基态能量，数值为： $E_1 \approx-13.6 \mathrm{eV}$ 。

需注意的是：基态是能量最低的能级，其余能级均为激发态，激发态寿命一般很短，只有几纳秒。

三、氢原子速度

根据氢原子的所受库仑力为氢原子电子提供向心力，可得： $\frac{1}{4 \pi \varepsilon_0} \cdot \frac{Z e^2}{r_n^2}=m_e \frac{v_n^2}{r_n}$ ；

依据上式，可得电子运行速度为： $v_n=\sqrt{\frac{Z e^2}{4 \pi \varepsilon_0 m_e r_n}}$

一中已知电子的轨道半径为： $r_n=\frac{4 \pi \varepsilon_0 h^2}{4 \pi^2 m_e e^2} n^2$

将轨道半径公式带入电子运行速度公式可以得到：

$v_n=\frac{e^2}{4 \pi \varepsilon_0 \cdot \hbar} \frac{1}{n}=\frac{e^2 c}{4 \pi \varepsilon_0 \cdot \hbar c} \frac{1}{n}=\frac{\alpha c}{n}$ ，其中 $\alpha=\frac{e^2}{4 \pi \varepsilon_0 \cdot \hbar \cdot c}$