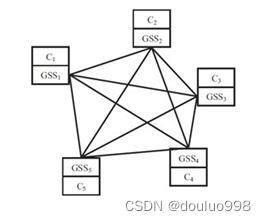
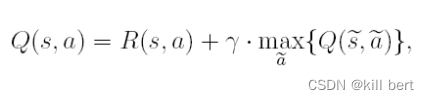目录
前言
文献阅读 :基于动态分类的长短期记忆网络模型,用于不同气候区日流量预报
背景
主要贡献
思路
动态分类 (DC) 方法
DC-LSTM 和 DC-B-LSTM 模型
Box -Cox数据转换
模型性能评估指标
克里金插值源码总结
第一部分
第二部分
第三部分
总结
前言
This week I read an article that introduced a new integrated modeling method called DC-LSTM model, which combines dynamic classification and LSTM deep learning models. The goal is to improve traffic prediction by more accurately classifying data into low, medium, and high flow states. In addition, before applying the LSTM model (DC-B-LSTM model), Box-Cox transformation is used to convert non-normal distribution of flow data to further improve the model performance. This week, I continued to analyze the source code of Kriging interpolation and hope to make modular improvements based on a clear understanding of the source code.
本周我读了一篇文章,这篇文章说的是开发了一种将动态分类方法与LSTM深度学习模型相结合的新型集成建模方法(DC-LSTM模型),通过更准确地将数据分类为低、中、高流状态来改进流量预测。此外,在应用 LSTM 模型(DC-B-LSTM 模型)之前,使用 Box-Cox 变换转换非正态分布的流数据,以进一步提高模型性能。本周继续对克里金插值的源码展开分析,希望在能够分析清楚源码的基础上进行模块化的改进。
文献阅读 :基于动态分类的长短期记忆网络模型,用于不同气候区日流量预报
--Haibo Chu, Jin Wu, Wenyan Wu, Jiahua Wei,
A dynamic classification-based long short-term memory network model for daily streamflow forecasting in different climate regions,
Ecological Indicators,
Volume 148,
2023,
110092,
ISSN 1470-160X,
https://doi.org/10.1016/j.ecolind.2023.110092.
背景
日流量预报是决定流水生态过程、健康溪流生态和周边环境的重要因素,准确的河流量预报为生态评估、管理和决策提供了有力的基础。最近,针对不同流态的数据驱动模型在流量预测方面显示出巨大的潜力。然而,不同流态之间的边界是任意选择的,没有考虑现实世界中经常随时间变化的边界变化。
主要贡献
- 适用于日常的新型混合动力型 DC-LSTM集成建模开发预测。
- 检查该模型以预测不同气候区域的流量。
- 集成 LSTM 和动态分类可以提高流量预测的性能。
- Box -Cox数据转换可以进一步提高干旱地区的模型性能。
思路
该文提出一种将动态分类方法与无需数据转换的长短期记忆网络(LSTM)模型(DC-LSTM模型)和具有Box-Cox数据变换的LSTM(DC-B-LSTM模型)耦合的集成建模方法,以提高考虑不同流态的流量预测性能。动态分类的边界是相关水文变量的动态变化区间值,传统分类方法仅使用静态单变量阈值,因此动态分类可以更充分地探索水文数据的关系和信息。
动态分类 (DC) 方法
采用动态分类方法表示三种不同流态,没有明确的边界(如降雨量、径流或降雨径流比等水文变量的常数值),并根据获得的模型性能评价指标自动调整边界。边界是相关水文变量的动态变化间隔值。它是在传统的静态单变量阈值分类方法的基础上开发的。基于阈值的分类方法的详细信息由 Chu 等人 (2021) 提供。但是,与传统的静态分类不同,动态分类不使用静态阈值来定义不同流态之间的边界。传统静态分类方法和动态分类方法之间的区别可以用一个例子来最好地解释。
假设有200个降水流样本,范围为0-100 mm,基于静态分类方法,根据预定义的阈值将样本分为20个子集,如80 mm和0 mm。换句话说,如果降水值在 20 和 1 mm 的范围内,则样本将被分类为子集 21;如果降水值在 80 和 2 mm 范围内,则样本将被分类为子集 81,如果降水值在 100 和 3 mm 范围内,则样本将被分类为子集 1。但是,基于动态分类方法,阈值的设置方式允许不同数据子集之间的重叠。例如,子集 0 的降水范围可以定义为 [30, 2 mm],子集 20 的降水范围可以定义为 [80 mm, 3 mm],子集 70 的降水范围可以定义为 [100 mm, <> mm]。不同数据子集之间的阈值和重叠可以根据不同预测模型的性能需求进行动态调整。根据上述分类方案,相关模型性能评价指标,如相关系数(R2),对于示例,可能达到 0.70,但所需的值可能是 0.80;因此,子集 1、2 和 3 的降水范围可分别调整为 [0, 35 mm]、[25 mm, 75 mm] 和 [65 mm, 100 mm]。然后,可以使用新的分类结果训练 LSTM 模型,直到满足性能要求。通过这种方式,动态分类导致数据子集在没有明确边界的情况下最佳地表示三种不同的流态,从而充分反映了现实世界中不同流态之间边界的模糊性。
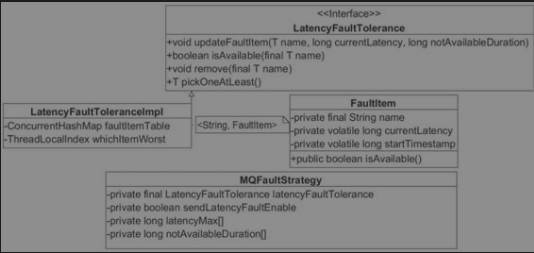
DC-LSTM 和 DC-B-LSTM 模型
开发了一种将动态分类方法和LSTM深度学习方法(无需数据转换的DC-LSTM模型)相结合的集成建模方法,以改进流流预测。第一步,动态分类方法用于将所有样品分类为三个子集,这些子集根据低、中和高流制度的预定义阈值定义重叠范围。在第二步中,训练 LSTM 模型以映射每个流态中每个影响变量和流之间的关系。第三步,如果不满足所选预测模型的性能要求,则动态调整不同数据子集的阈值。然后,使用新的分类子集训练 LSTM 模型,直到满足性能要求。
Box -Cox数据转换
然而,在许多情况下,溪流序列不服从正态分布并且高度偏斜,这将影响使用数据驱动方法进行溪流预测的准确性。因此,采用 Box–Cox 数据转换将偏态流数据转换为正态分布。Box-Cox 变换表示如下:

yt是原始变量,zt是转换后的变量,并且是博克斯-考克斯系数
因此,本研究基于DC-LSTM模型开发了DC-B-LSTM模型。在 DC-LSTM 模型中的第一步之后,将添加一个额外的步骤。Box–Cox 函数用于将非正态分布的数据流数据转换为近似正态分布的数据。然后,开发LSTM模型,并动态调整阈值,直到满足性能要求。DC-LSTM和DC-B-LSTM模型的示意图如图3所示。

模型性能评估指标

克里金插值源码总结
第一部分
1.首先是导入模块和函数,是实现克里金插值的工具
2.定义了许多函数,并且给了默认值
3.配置伪逆变量
在克里金插值中,伪逆矩阵是一个关键的工具,用来求解预测点处的属性值。
4.建立初始的变差函数模型和参数(变差函数就是半方差函数)
5.检查有没有给出GSTools协方差模型
GSTools是一个Python库,用于生成几何和空间统计模型。其中包括一些经典的协方差函数(也称为协方差模型),如指数、高斯和球形等。协方差函数描述了不同空间点之间的相关性,可以用来建立克里金插值模型,在地质学、气象学、水文学等领域广泛应用。
6.保存模型,并且保证模型是一维或者二维的。
7.检查坐标类型是否匹配
8.把x,y,z转化成一维数组
9.调整各向异性,并且调整了x,y
10.数据预处理,计算出已知点之间的半方差值
11.确定目前使用的变差函数模型和参数
12.给出了计算delta,sigma和espilon的方法,并且用这些值可以计算克里金插值预测误差的统计量:Q1,Q2,cR。
第二部分
1.更新变差函数模型
2.建立模型和参数
3.检验是否给出协方差模型
4.保存模型
5.检查坐标类型是否匹配
6.检查输入的各向异性缩放和角度参数与当前实例中的参数是否相同,并修改
7.数据预处理(跟第一部分的一样)
首先将参数格式修改到合适的,然后初始化变差模型,计算距离和方差
该函数采用 self.X_ADJUSTED、self.Y_ADJUSTED 和 self.Z 等参数来计算半方差函数(semivariance)和变差函数(variogram),并返回计算结果及变差模型的参数。
8.输出模型的具体参数信息
9.计算统计量
delta:点对之间的距离sigma:所有以 delta 距离分隔的点对的平均半方差epsilon:实验半方差和相同距离处的计算半方差之间的差值。
然后使用这些值计算 Q1、Q2 和 cR。
10.绘制变差函数模型和实际分组数据的图形
11.在滞后距离上计算变差函数的值
滞后距离是用来描述相邻样本点之间的距离关系的,它通常会在半方差函数的计算中被使用到。具体地说,对于每个h值,可以计算出所有距离为hi=h的样本点对的半方差值,然后取平均值作为该值下的半方差函数值。这样就得到了一组关于
的半方差函数值,从而可以进一步建立克里金插值模型。
12.在打印输出时切换对话模式,在绘图时切换绘图模式(不重要)
13.拟合残差值,并绘制变差函数拟合的残差值图
在克里金插值中,拟合残差值是指预测值与实际值之间的差异。在进行克里金插值时,通常会使用部分样本点来训练模型,然后用剩余的样本点测试模型的预测效果。如果预测值与实际值之间存在较大误差,说明训练出的模型不够准确,需要对其进行优化。
14.返回变差函数拟合的Q1、Q2和cR三个统计量,打印变差函数拟合的Q1、Q2和cR三个统计量
第三部分
1.组装克里金矩阵
先生成xy二维数组,然后计算出每两个点之间的距离
创建一个(n+1)×(n+1)的二维矩阵a,元素均初始化为0。其中,前n行、前n列分别为从点集中选出的n个点之间的半方差,而第n+1行、第n+1列则表示未知点与其他点之间的半方差。
遍历矩阵a的前n行和前n列,用半方差公式计算每对已知点之间的半方差,并将结果赋给相应的a元素;再将主对角线上的所有元素设为0;最后,将第n+1行和第n+1列的所有元素设为1,将a[n, n]设为0。
2.克里金的解法,一共三种,求预测值z和方差:
2-1方法_exec_vector将kriging系统作为矢量化操作进行求解
2-2方法_exec_loop通过循环遍历所有指定点来解决kriging系统
2-3方法_exec_loop_moving_window通过循环遍历所有指定点来解决kriging系统,但与_exec_loop方法不同,该方法使用了移动窗口技术来减少计算量。
3.Ordinary Kriging的插值方法
总结
想要做出LSTM-Kriging模型,有两个要求
第一,训练出一个LSTM模型用以模拟高斯扩散模型
第二,使用LSTM替换克里金插值过程中的半方差函数拟合方法
目前的难点是如何优化克里金插值的半方差拟合过程,希望在下周可以有新的进展。