题目链接

Leetcode.2280 表示一个折线图的最少线段数 Rating ： 1681

题目描述

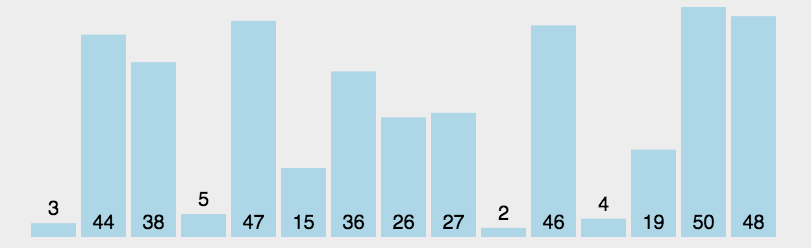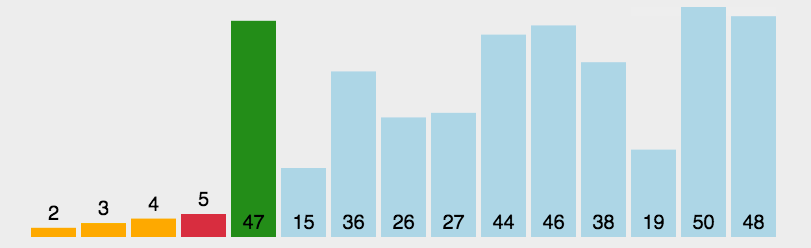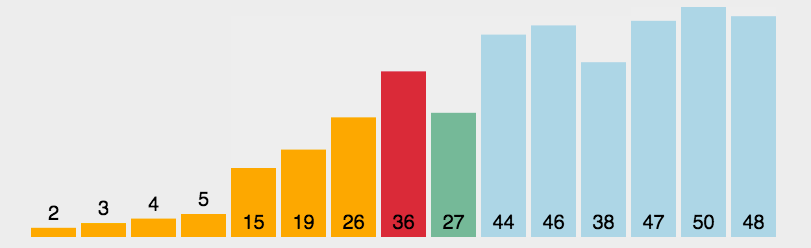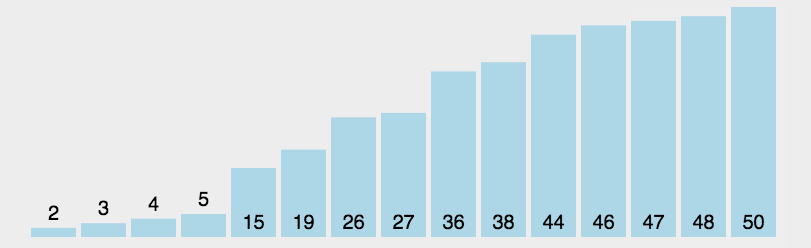
给你一个二维整数数组 stockPrices，其中 stockPrices[i] = [dayi, pricei]表示股票在 dayi的价格为 pricei 。折线图 是一个二维平面上的若干个点组成的图，横坐标表示日期，纵坐标表示价格，折线图由相邻的点连接而成。比方说下图是一个例子：

请你返回要表示一个折线图所需要的 最少线段数 。

示例 1：

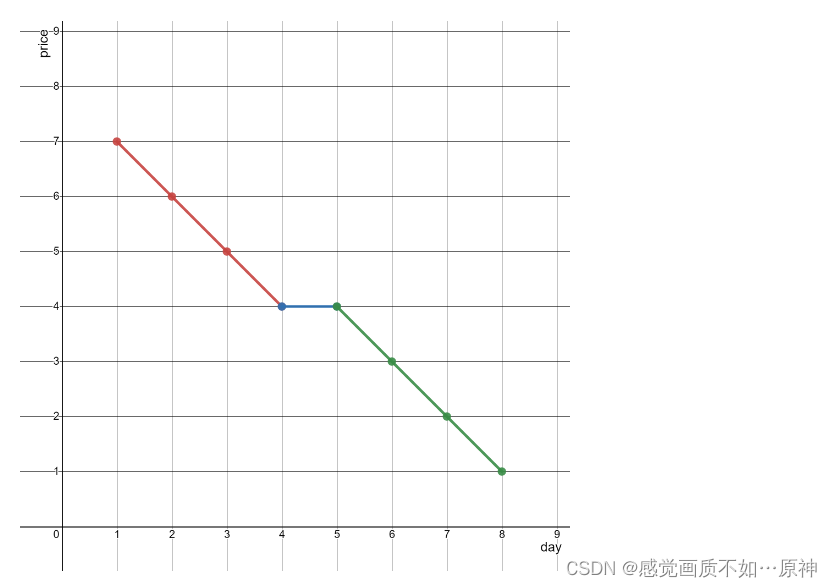
输入：stockPrices = [[1,7],[2,6],[3,5],[4,4],[5,4],[6,3],[7,2],[8,1]]
输出：3
解释：
上图为输入对应的图，横坐标表示日期，纵坐标表示价格。
以下 3 个线段可以表示折线图：

• 线段 1 （红色）从 (1,7) 到 (4,4) ，经过 (1,7) ，(2,6) ，(3,5) 和 (4,4) 。
• 线段 2 （蓝色）从 (4,4) 到 (5,4) 。
• 线段 3 （绿色）从 (5,4) 到 (8,1) ，经过 (5,4) ，(6,3) ，(7,2) 和 (8,1) 。 可以证明，无法用少于 3 条线段表示这个折线图。

示例 2：

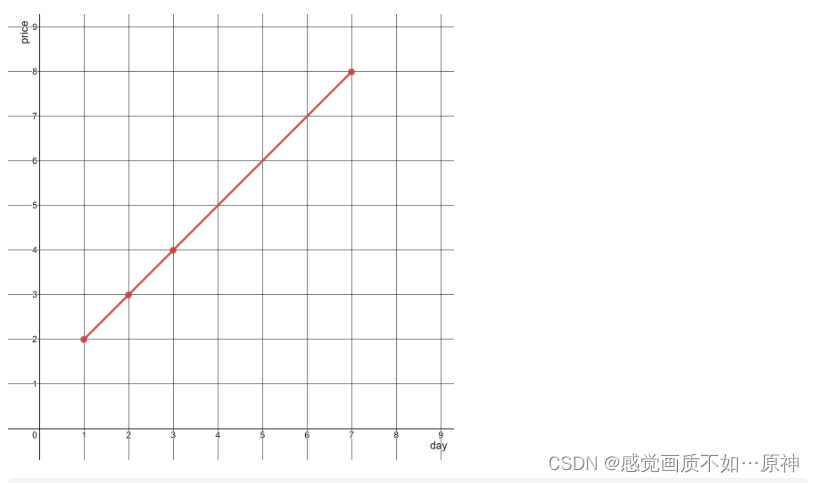
输入：stockPrices = [[3,4],[1,2],[7,8],[2,3]]
输出：1
解释：
如上图所示，折线图可以用一条线段表示。

提示：

• $1<=stockPrices.length<=10^5$
• $stockPrices[i].length==2$
• $1<=dayi,pricei<=10^9$
• 所有 dayi互不相同 。

解法：排序+几何

我们只需要判断给定的坐标连成的线段中有多少个不同的 斜率，就能得出答案。

对于两点 $(x1,y1)和(x2,y2)$ ，他们之间连成的线段的斜率 $k=\frac{y2-y1}{x2-x1}$。

对于三个点 $(x1,y1)和(x2,y2)和(x3,y3)$，只需要判断前两个点的斜率 和 后两个点的斜率是否相同，就可以判断出它们是否在同一条直线上，即 $\frac{y2-y1}{x2-x1}=\frac{y3-y2}{x3-x2}$。

由于计算机中的除法是有精度问题的。所以我们为了避免这种问题，就将原式的除法 改为 乘法。即$(x2-x1)(y3-y2)=(y2-y1)(x3-x2)$，我们只需要判断这个是否成立即可。

我们先将 $stockPrices$ 按 $x$ 坐标，从小到大排序，将相邻的点挨到一起，模拟上述的过程即可。

时间复杂度： $O(nlogn)$

C++代码：

class Solution {
public:
    int minimumLines(vector<vector<int>>& s) {
        int n = s.size();
        //如果只有一个点，那就不存在线段
        if(n == 1) return 0;
        
        //最开始是有一条线段的
        int ans = 1;
        sort(s.begin(),s.end());

        for(int i = 0;i < n - 2;i++){
            int x1 = s[i][0] , y1 = s[i][1];
            int x2 = s[i+1][0] , y2 = s[i+1][1];
            int x3 = s[i+2][0] , y3 = s[i+2][1];

            //*1LL 是为了将乘积转成 long long，防止爆int
            //如果不等于，说明这三点不共线，那么线段数量就要 +1 
            if((x2 - x1) * 1LL *(y3 - y2) != (y2 - y1) * 1LL *(x3 - x2)) ans++;
        }

        return ans;
    }
};