1. 算法原理
1.1 2D坐标与3D坐标的关系
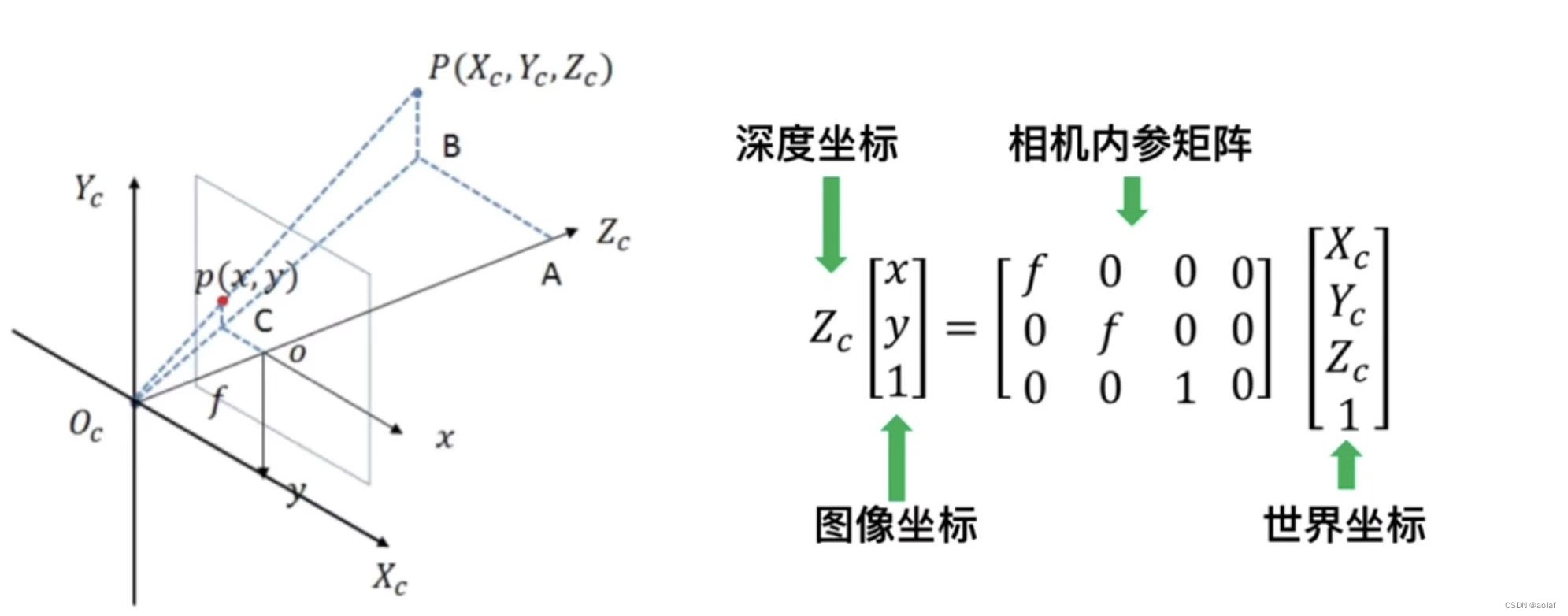
如图,已知世界坐标系上的某点P(Xc, Yc, Zc)经过相机的内参矩阵可以获得唯一的图像坐标p(x, y),但是反过来已知图像上某点p(x, y),无法获得唯一的世界坐标(只能知道P在Ocp这一射线上),只有当深度坐标Zc已知时,我们才可求得唯一的世界坐标P,因此2D坐标往3D坐标的转换多围绕Zc的获取展开。
1.2 LSS原理
LSS这篇论文的核心是通过lift模块显式估计图像的深度信息,将2D往3D映射的射线离散化为D段,每段都对应深度的概率分布,从而实现2D图像坐标向3D世界坐标的转换,利用splat模块完成从3D到BEV空间的特征映射,最终利用shoot模块完成自动驾驶中的语义分割任务。
2. 算法流程
2.1 2D转3D(lift)
2.1.1 生成视锥点云
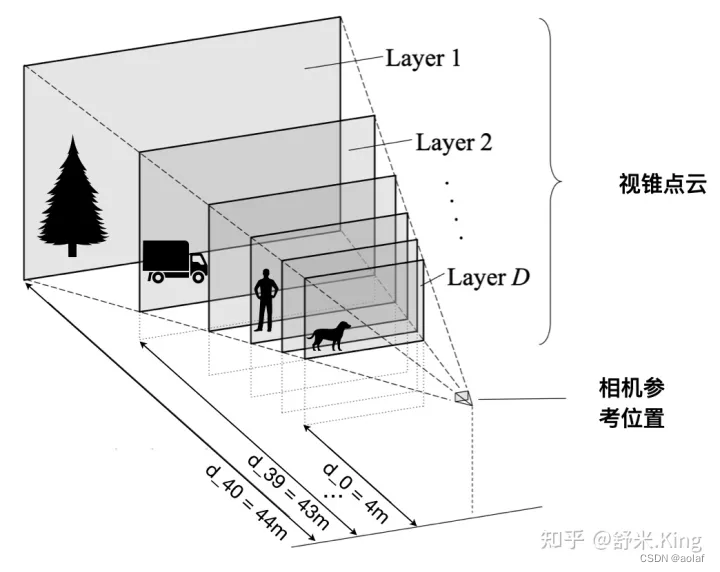
①. 在深度方向上给每个图像点预测一个离散的深度信息(4m~45m,间隔为1m),这样就获得了41个离散的深度值,同时根据对原图的1/16下采样,在x、y方向上划分22*8的网格,将他们stack在一起,便可获得视锥frustum 。
def create_frustum():
# 原始图片大小 ogfH:128 ogfW:352
ogfH, ogfW = self.data_aug_conf['final_dim']
# 下采样16倍后图像大小 fH: 8 fW: 22
fH, fW = ogfH // self.downsample, ogfW // self.downsample
# self.grid_conf['dbound'] = [4, 45, 1]
# 在深度方向上划分网格 ds: DxfHxfW (41x8x22)
ds = torch.arange(*self.grid_conf['dbound'], dtype=torch.float).view(-1, 1, 1).expand(-1, fH, fW)
D, _, _ = ds.shape # D: 41 表示深度方向上网格的数量
"""
1. torch.linspace(0, ogfW - 1, fW, dtype=torch.float)
tensor([0.0000, 16.7143, 33.4286, 50.1429, 66.8571, 83.5714, 100.2857,
117.0000, 133.7143, 150.4286, 167.1429, 183.8571, 200.5714, 217.2857,
234.0000, 250.7143, 267.4286, 284.1429, 300.8571, 317.5714, 334.2857,
351.0000])
2. torch.linspace(0, ogfH - 1, fH, dtype=torch.float)
tensor([0.0000, 18.1429, 36.2857, 54.4286, 72.5714, 90.7143, 108.8571,
127.0000])
"""
# 在0到351上划分22个格子 xs: DxfHxfW(41x8x22)
xs = torch.linspace(0, ogfW - 1, fW, dtype=torch.float).view(1, 1, fW).expand(D, fH, fW)
# 在0到127上划分8个格子 ys: DxfHxfW(41x8x22)
ys = torch.linspace(0, ogfH - 1, fH, dtype=torch.float).view(1, fH, 1).expand(D, fH, fW)
# D x H x W x 3
# 堆积起来形成网格坐标, frustum[i,j,k,0]就是(i,j)位置,深度为k的像素的宽度方向上的栅格坐标 frustum: DxfHxfWx3
frustum = torch.stack((xs, ys, ds), -1)
return nn.Parameter(frustum, requires_grad=False)
②. 利用相机内、外参,将基于图像坐标系的视锥转换为车辆坐标系下的空间位置来表示,其维度也是HxWxDx3,即HxWxD个[x, y, z]。
def get_geometry(self, rots, trans, intrins, post_rots, post_trans):
B, N, _ = trans.shape # B: batch size N:环视相机个数
# undo post-transformation
# B x N x D x H x W x 3
# 抵消数据增强及预处理对像素的变化
points = self.frustum - post_trans.view(B, N, 1, 1, 1, 3)
points = torch.inverse(post_rots).view(B, N, 1, 1, 1, 3, 3).matmul(points.unsqueeze(-1))
# 图像坐标系 -> 归一化相机坐标系 -> 相机坐标系 -> 车身坐标系
# 但是自认为由于转换过程是线性的,所以反归一化是在图像坐标系完成的,然后再利用
# 求完逆的内参投影回相机坐标系
points = torch.cat((points[:, :, :, :, :, :2] * points[:, :, :, :, :, 2:3],
points[:, :, :, :, :, 2:3]
), 5) # 反归一化
combine = rots.matmul(torch.inverse(intrins))
points = combine.view(B, N, 1, 1, 1, 3, 3).matmul(points).squeeze(-1)
points += trans.view(B, N, 1, 1, 1, 3)
# (bs, N, depth, H, W, 3):其物理含义
# 每个batch中的每个环视相机图像特征点,其在不同深度下位置对应
# 在ego坐标系下的坐标
return points
2.1.2 给视锥点云上的每个点生成特征
①. 利用Efficientnet-B0主干网络对环视图像进行特征提取。同时借鉴FPN的思想将1/32层上采样与1/16层进行特征融合,获得 [B * N, 512, H / 16, W / 16]的特征输出层。
②. 利用1*1进行通道缩放,将输出的512通道变为105(41 + 64),其中41代表深度特征,64代表语义特征。
③. 将深度特征进行softmax获得深度信息的概率分布。
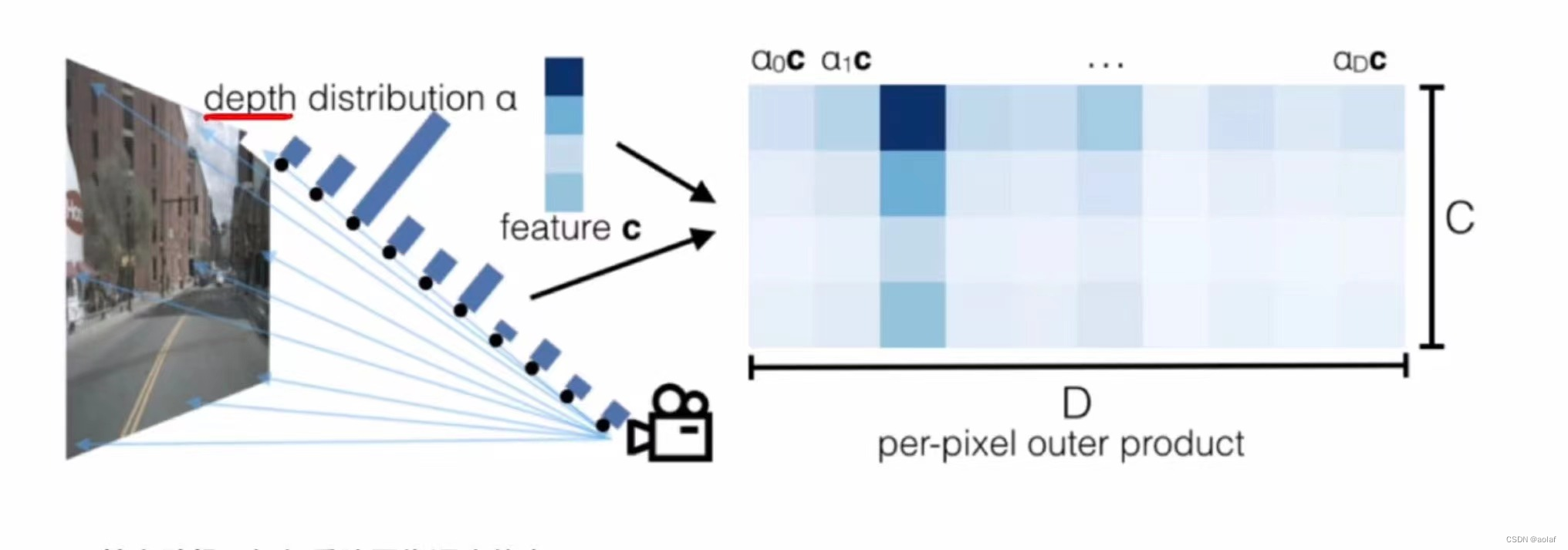
④. 深度概率分布与语义特征作外积,构建点云特征。
如下图中,第三个深度(α2)的概率分布最高,因此α2c的特征最显著。
2.2 3D转BEV(splat)
有了视锥点云特征,就可以根据视锥点的空间位置把每个视锥点的特征放到BEV网格中的合适位置,组成BEV特征图。
BEV网格由200x200个格子(BEV Pillar)组成,每个格子对应物理尺寸为0.5米x0.5米。即BEV网格对应车辆前、后和左、右各50m,且高度不限的3维空间。
上面通过相机的内外参,已经把视锥点云转换到车辆坐标系下的空间位置。排除掉BEV网格所表示空间范围(以自车为中心100mx100m范围)以外的点,就可以把剩余有效的视锥点云分配到每个BEV Pillar里。
注意,这里存在同一个BEV Pillar可能分配多个视锥点的情况,这是由两个原因引起:
1. 单张2D图像不同的像素点可能投影在俯视图中的同一个位置,例如垂直于地面的电线杆,它成像的多个像素点可能投到同一个BEV Pillar。
2. 相邻两相机有部分成像区域重叠,相机图像中的不同像素点投影在同一个BEV Pillar。例如不同相机画面中的同一个目标。
对于一个BEV Pillar分配多个视锥点,使用QuickCumsum的方法,把视锥点的特征相加,最后得到了200x200xC的BEV特征图,源码中C取64。
def voxel_pooling(self, geom_feats, x):
# geom_feats;(B x N x D x H x W x 3):在ego坐标系下的坐标点;
# x;(B x N x D x fH x fW x C):图像点云特征
B, N, D, H, W, C = x.shape
Nprime = B*N*D*H*W
# 将特征点云展平,一共有 B*N*D*H*W 个点
x = x.reshape(Nprime, C)
# ego下的空间坐标转换到体素坐标(范围从-50m~50m,转换为0-200的体素坐标)
geom_feats = ((geom_feats - (self.bx - self.dx/2.)) / self.dx).long()
# 将体素坐标同样展平,geom_feats: (B*N*D*H*W, 3)
geom_feats = geom_feats.view(Nprime, 3)
# 每个点对应于哪个batch
batch_ix = torch.cat([torch.full([Nprime//B, 1], ix,device=x.device,dtype=torch.long) for ix in range(B)])
# geom_feats: (B*N*D*H*W, 4)
geom_feats = torch.cat((geom_feats, batch_ix), 1)
# 过滤掉在边界线之外的点 x:0~199 y: 0~199 z: 0
kept = (geom_feats[:, 0] >= 0) & (geom_feats[:, 0] < self.nx[0])\
& (geom_feats[:, 1] >= 0) & (geom_feats[:, 1] < self.nx[1])\
& (geom_feats[:, 2] >= 0) & (geom_feats[:, 2] < self.nx[2])
x = x[kept]
geom_feats = geom_feats[kept]
# 给每一个点一个rank值,rank相等的点在同一个batch,并且在在同一个格子里面
ranks = geom_feats[:, 0] * (self.nx[1] * self.nx[2] * B)\
+ geom_feats[:, 1] * (self.nx[2] * B)\
+ geom_feats[:, 2] * B\
+ geom_feats[:, 3]
# 按照rank排序,这样rank相近的点就在一起了
sorts = ranks.argsort()
x, geom_feats, ranks = x[sorts], geom_feats[sorts], ranks[sorts]
# 对每个体素中的点云特征进行QuickCumsum,输出去重之后的Voxel特征,BxCxZxXxY。
if not self.use_quickcumsum:
x, geom_feats = cumsum_trick(x, geom_feats, ranks)
else:
x, geom_feats = QuickCumsum.apply(x, geom_feats, ranks)
# final (B x C x Z x X x Y)
final = torch.zeros((B, C, self.nx[2], self.nx[0], self.nx[1]), device=x.device)
# 将x按照网格坐标放到final中
final[geom_feats[:, 3], :, geom_feats[:, 2], geom_feats[:, 0], geom_feats[:, 1]] = x
# 消除掉z维,B x C x 200 x 200
final = torch.cat(final.unbind(dim=2), 1)
return final
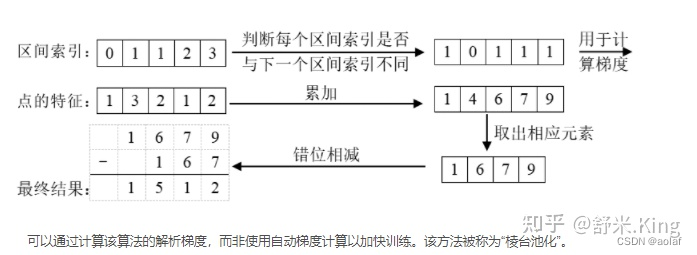
cumsum_trick(): 池化累积求和技巧
模型中使用Pillar累积求和池化,“累积求和”是通过bin id 对所有点进行排序,对所有特征执行累积求和,然后减去 bin 部分边界处的累积求和值来执行求和池化。无需依赖 autograd 通过所有三个步骤进行反向传播,而是可以导出整个模块的分析梯度,从而将训练速度提高 2 倍。 该层被称为“Frustum Pooling”,因为它将 n 个图像产生的截锥体转换为与摄像机数量 n 无关的固定维度 CxHxW 张量。
计算原理的过程示意图: