文章目录

周赛341
- [6376. 一最多的行](https://leetcode.cn/problems/row-with-maximum-ones/)
- - 暴力模拟
- [6350. 找出可整除性得分最大的整数](https://leetcode.cn/problems/find-the-maximum-divisibility-score/)
- - 暴力模拟
- [6375. 构造有效字符串的最少插入数](https://leetcode.cn/problems/minimum-additions-to-make-valid-string/)
- - 丑陋的模拟
  - 法1. 双指针匹配
  - 法2. 考虑abc的周期数
- 🎃[6378. 最小化旅行的价格总和](https://leetcode.cn/problems/minimize-the-total-price-of-the-trips/)
- - 法1. 树形DP（类似打家劫舍Ⅲ）
  - 法2. 树上差分 + Tarjan离线LCA
- [337. 打家劫舍 III](https://leetcode.cn/problems/house-robber-iii/)

周赛341

6376. 一最多的行

难度简单0

给你一个大小为 m x n 的二进制矩阵 mat ，请你找出包含最多 1 的行的下标（从 0 开始）以及这一行中 1 的数目。

如果有多行包含最多的 1 ，只需要选择 行下标最小 的那一行。

返回一个由行下标和该行中 1 的数量组成的数组。

示例 1：

输入：mat = [[0,1],[1,0]]
输出：[0,1]
解释：两行中 1 的数量相同。所以返回下标最小的行，下标为 0 。该行 1 的数量为 1 。所以，答案为 [0,1] 。

示例 2：

输入：mat = [[0,0,0],[0,1,1]]
输出：[1,2]
解释：下标为 1 的行中 1 的数量最多。该行 1 的数量为 2 。所以，答案为 [1,2] 。

示例 3：

输入：mat = [[0,0],[1,1],[0,0]]
输出：[1,2]
解释：下标为 1 的行中 1 的数量最多。该行 1 的数量为 2 。所以，答案为 [1,2] 。

提示：

m == mat.length
n == mat[i].length
1 <= m, n <= 100
mat[i][j] 为 0 或 1

暴力模拟

class Solution {
    public int[] rowAndMaximumOnes(int[][] mat) {
        int max = 0, idx = 0;
        for(int i = 0; i < mat.length; i++){
            int cnt = 0;
            for(int j = 0; j < mat[0].length; j++){
                if(mat[i][j] == 1) cnt++;
            }
            if(cnt > max){
                max = cnt;
                idx = i;
            }
        }
        return new int[]{idx, max};
    }
}

6350. 找出可整除性得分最大的整数

难度简单0

给你两个下标从 0 开始的整数数组 nums 和 divisors 。

divisors[i] 的 可整除性得分 等于满足 nums[j] 能被 divisors[i] 整除的下标 j 的数量。

返回 可整除性得分 最大的整数 divisors[i] 。如果有多个整数具有最大得分，则返回数值最小的一个。

示例 1：

输入：nums = [4,7,9,3,9], divisors = [5,2,3]
输出：3
解释：divisors 中每个元素的可整除性得分为：
divisors[0] 的可整除性得分为 0 ，因为 nums 中没有任何数字能被 5 整除。
divisors[1] 的可整除性得分为 1 ，因为 nums[0] 能被 2 整除。 
divisors[2] 的可整除性得分为 3 ，因为 nums[2]、nums[3] 和 nums[4] 都能被 3 整除。 
因此，返回 divisors[2] ，它的可整除性得分最大。

示例 2：

输入：nums = [20,14,21,10], divisors = [5,7,5]
输出：5
解释：divisors 中每个元素的可整除性得分为：
divisors[0] 的可整除性得分为 2 ，因为 nums[0] 和 nums[3] 都能被 5 整除。
divisors[1] 的可整除性得分为 2 ，因为 nums[1] 和 nums[2] 都能被 7 整除。
divisors[2] 的可整除性得分为 2 ，因为 nums[0] 和 nums[3] 都能被5整除。 
由于 divisors[0]、divisors[1] 和 divisors[2] 的可整除性得分都是最大的，因此，我们返回数值最小的一个，即 divisors[2] 。

示例 3：

输入：nums = [12], divisors = [10,16]
输出：10
解释：divisors 中每个元素的可整除性得分为：
divisors[0] 的可整除性得分为 0 ，因为 nums 中没有任何数字能被 10 整除。
divisors[1] 的可整除性得分为 0 ，因为 nums 中没有任何数字能被 16 整除。 
由于 divisors[0] 和 divisors[1] 的可整除性得分都是最大的，因此，我们返回数值最小的一个，即 divisors[0] 。

提示：

1 <= nums.length, divisors.length <= 1000
1 <= nums[i], divisors[i] <= 109

暴力模拟

class Solution {
    public int maxDivScore(int[] nums, int[] divisors) {
        int res = Integer.MAX_VALUE, sc = 0;
        for(int i = 0; i < divisors.length; i++){
            int cnt = 0;
            int d = divisors[i];
            for(int j = 0; j < nums.length; j++){
                if(nums[j] % d == 0) cnt++;
            }
            if(cnt > sc){
                res = d;
                sc = cnt;
            }else if (cnt == sc){
                res = Math.min(res, d);
            }
        }
        return res;
    }
}

6375. 构造有效字符串的最少插入数

难度中等1

给你一个字符串 word ，你可以向其中任何位置插入 “a”、“b” 或 “c” 任意次，返回使 word 有效需要插入的最少字母数。

如果字符串可以由 “abc” 串联多次得到，则认为该字符串有效。

示例 1：

输入：word = "b"
输出：2
解释：在 "b" 之前插入 "a" ，在 "b" 之后插入 "c" 可以得到有效字符串 "abc" 。

示例 2：

输入：word = "aaa"
输出：6
解释：在每个 "a" 之后依次插入 "b" 和 "c" 可以得到有效字符串 "abcabcabc" 。

示例 3：

输入：word = "abc"
输出：0
解释：word 已经是有效字符串，不需要进行修改。

提示：

1 <= word.length <= 50
word 仅由字母 “a”、“b” 和 “c” 组成。

丑陋的模拟

class Solution {
    public int addMinimum(String word) {
        int res = 0;
        int n = word.length();
        char[] arr = word.toCharArray();
        int i = 0;
        // 枚举每一次abc
        while(i < n){
            if(arr[i] == 'a'){
                if(i + 1 < n && arr[i+1] == 'b'){
                    if(i + 2 < n && arr[i+2] == 'c'){
                        i = i + 2;
                    }else{
                        res++;
                        i = i + 1;
                    }
                }else if(i + 1 < n && arr[i+1] == 'c'){
                    i += 1;
                    res += 1;
                }else{
                    res += 2;
                }
            }else if(arr[i] == 'b'){
                res++;
                if(i + 1 < n && arr[i+1] == 'c'){
                    i++;
                }else{
                    res += 1;
                }
            }else{
                res += 2;
            }
            i++;
        }
        return res;
    }
}

法1. 双指针匹配

https://leetcode.cn/circle/discuss/LkGd0z/

实就是把abcabcabc…这个串和word进行比对，分别对应两个下标指针j，i。如果在此刻出现了一样的字符 pattern[j]==word[i] ，那肯定i和j一起移动更优，否则就j单独移动。

class Solution {
    public int addMinimum(String word) {
        char[] pattern = new char[]{'a', 'b', 'c'};
        int i = 0, j = 0, res = 0;
        while(i < word.length()){
            if(word.charAt(i) == pattern[j]){
                i++;
            }else{
                res++; // 当s[i]!=word[j],需要插入一个元素，i不变
            }
            j = (j+1)%3; // 模式串按abcabc的顺序遍历
        }
        // i此时已经到达len了，j可能还没有
        // 如果j没有到达3，则说明word末尾还需要添加(3-j)个元素
        return res + (3-j)%3;
    }
}

法2. 考虑abc的周期数

class Solution {
    // 最后答案一定是abc的周期数
    //
    // 算一下周期t，那么有效字符串的长度为3t，需要插入的字符个数为3t-n
    // 怎么思考？
    // 对于两个相邻字符x和y (x在y左侧) ，如果x<y，那么x和y可以在同一个“abc’周期内，否则一定不在
    // t就是 x >= y 的次数
    public int addMinimum(String word) {
        char[] s = word.toCharArray();
        int t = 1;
        for(int i = 1; i < s.length; i++){
            if(s[i-1] >= s[i]){ // 必须生成一个新的abc
                ++t;
            }
        }
        return 3*t - s.length;
    }
}

🎃6378. 最小化旅行的价格总和

难度困难4

现有一棵无向、无根的树，树中有 n 个节点，按从 0 到 n - 1 编号。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条边。

每个节点都关联一个价格。给你一个整数数组 price ，其中 price[i] 是第 i 个节点的价格。

给定路径的 价格总和 是该路径上所有节点的价格之和。

另给你一个二维整数数组 trips ，其中 trips[i] = [starti, endi] 表示您从节点 starti 开始第 i 次旅行，并通过任何你喜欢的路径前往节点 endi 。

在执行第一次旅行之前，你可以选择一些 非相邻节点 并将价格减半。

返回执行所有旅行的最小价格总和。

示例 1：

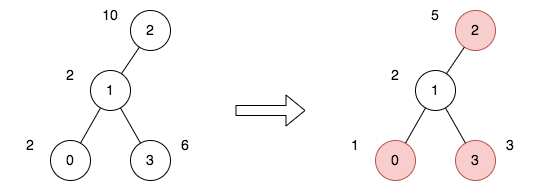
输入：n = 4, edges = [[0,1],[1,2],[1,3]], price = [2,2,10,6], trips = [[0,3],[2,1],[2,3]]
输出：23
解释：
上图表示将节点 2 视为根之后的树结构。第一个图表示初始树，第二个图表示选择节点 0 、2 和 3 并使其价格减半后的树。
第 1 次旅行，选择路径 [0,1,3] 。路径的价格总和为 1 + 2 + 3 = 6 。
第 2 次旅行，选择路径 [2,1] 。路径的价格总和为 2 + 5 = 7 。
第 3 次旅行，选择路径 [2,1,3] 。路径的价格总和为 5 + 2 + 3 = 10 。
所有旅行的价格总和为 6 + 7 + 10 = 23 。可以证明，23 是可以实现的最小答案。

示例 2：

输入：n = 2, edges = [[0,1]], price = [2,2], trips = [[0,0]]
输出：1
解释：
上图表示将节点 0 视为根之后的树结构。第一个图表示初始树，第二个图表示选择节点 0 并使其价格减半后的树。 
第 1 次旅行，选择路径 [0] 。路径的价格总和为 1 。 
所有旅行的价格总和为 1 。可以证明，1 是可以实现的最小答案。

提示：

1 <= n <= 50
edges.length == n - 1
0 <= ai, bi <= n - 1
edges 表示一棵有效的树
price.length == n
price[i] 是一个偶数
1 <= price[i] <= 1000
1 <= trips.length <= 100
0 <= starti, endi <= n - 1

法1. 树形DP（类似打家劫舍Ⅲ）

😭比赛时不知道怎么将价格减半，只会计算最短路

https://leetcode.cn/circle/discuss/LkGd0z/

经典题目之337. 打家劫舍 III的变形，数据范围很小，由于是树图，所以从x到y的路径有且只有一条，因为没有负权值边，不可能存在来回走然后削减代价的情况。预处理把路径统统求出来，把经过某点的次数记录进一个数组中，然后就是打家劫舍的经典树形dp了，选或不选的转移，如果在根节点选择打折，那么子节点只能选择不打折，如果在根节点不打折，那么子节点可以选择打折也可以选择不打折，两者取min。

题解：选择一些 非相邻节点 并将价格减半。 ==> 打家劫舍Ⅲ

class Solution {
    // 1. 计算每个点经过的次数 cnt（贡献法思想：计算每个点对答案能贡献多少）
    // 2. 写一个树形DP求答案
    private List<Integer>[] g;
    private int[] price, cnt;
    private int end;

    public int minimumTotalPrice(int n, int[][] edges, int[] price, int[][] trips) {
        g = new ArrayList[n];
        Arrays.setAll(g, e -> new ArrayList<>());
        for(int[] e : edges){
            int x = e[0], y = e[1];
            g[x].add(y);
            g[y].add(x); // 建树
        }
        this.price = price;

        // 1. 计算每个点经过的次数 cnt
        cnt = new int[n];
        for(int[] t : trips){
            end = t[1];
            path(t[0], -1);
        }
        // 2. 写一个树形DP求答案
        // 随便选一个点出发进行DP就可以了
        // 为什么？题目的描述与根节点无关
        int[] p = dfs(0, -1); 
        return Math.min(p[0], p[1]);

    }
    // 寻找路径，找到终点就返回True（注意树只有唯一的一条简单路径）
    // 寻找路径的同时标记源点到终点所有的点 +1
    private boolean path(int x, int fa) {
        if(x == end){ // 到达终点
            cnt[x]++; // 统计从 start 到 end 的路径上的点经过了多少次
            return true;
        }
        for(int y : g[x]){
            if(y != fa && path(y,x)){
                cnt[x]++; // 统计从 start 到 end 的路径上的点经过了多少次
                return true; // 找到终点
            }
        }
        return false; // 未找到终点
    }

    private int[] dfs(int x, int fa){
        int notHalve = price[x] * cnt[x]; // x 不变
        int halve = notHalve / 2; // x 减半
        for(int y : g[x]){
            if(y != fa){
                int[] p = dfs(y, x); // 计算 y 不变/减半的最小价值总和
                // x没有减半的话，y既可以减半，也可以不减半，取这两种情况的最小值
                notHalve += Math.min(p[0], p[1]);
                halve += p[0]; // x 减半，那么 y 只能不变
            }
        }
        return new int[]{notHalve, halve};
    }
}

法2. 树上差分 + Tarjan离线LCA

看不懂

题解：https://leetcode.cn/problems/minimize-the-total-price-of-the-trips/solution/lei-si-da-jia-jie-she-iii-pythonjavacgo-4k3wq/

class Solution {
    private List<Integer>[] g, qs;
    private int[] diff, father, color, price;

    public int minimumTotalPrice(int n, int[][] edges, int[] price, int[][] trips) {
        g = new ArrayList[n];
        Arrays.setAll(g, e -> new ArrayList<>());
        for (var e : edges) {
            int x = e[0], y = e[1];
            g[x].add(y);
            g[y].add(x); // 建树
        }

        qs = new ArrayList[n];
        Arrays.setAll(qs, e -> new ArrayList<>());
        for (var t : trips) {
            int x = t[0], y = t[1];
            qs[x].add(y); // 路径端点分组
            if (x != y) qs[y].add(x);
        }

        pa = new int[n];
        for (int i = 1; i < n; ++i)
            pa[i] = i;

        diff = new int[n];
        father = new int[n];
        color = new int[n];
        tarjan(0, -1);

        this.price = price;
        var p = dfs(0, -1);
        return Math.min(p[0], p[1]);
    }

    // 并查集模板
    private int[] pa;

    private int find(int x) {
        if (pa[x] != x)
            pa[x] = find(pa[x]);
        return pa[x];
    }

    private void tarjan(int x, int fa) {
        father[x] = fa;
        color[x] = 1; // 递归中
        for (int y : g[x])
            if (color[y] == 0) { // 未递归
                tarjan(y, x);
                pa[y] = x; // 相当于把 y 的子树节点全部 merge 到 x
            }
        for (int y : qs[x])
            // color[y] == 2 意味着 y 所在子树已经遍历完
            // 也就意味着 y 已经 merge 到它和 x 的 lca 上了
            if (y == x || color[y] == 2) { // 从 y 向上到达 lca 然后拐弯向下到达 x
                ++diff[x];
                ++diff[y];
                int lca = find(y);
                --diff[lca];
                int f = father[lca];
                if (f >= 0) {
                    --diff[f];
                }
            }
        color[x] = 2; // 递归结束
    }

    private int[] dfs(int x, int fa) {
        int notHalve = 0, halve = 0, cnt = diff[x];
        for (int y : g[x])
            if (y != fa) {
                var p = dfs(y, x); // 计算 y 不变/减半的最小价值总和
                notHalve += Math.min(p[0], p[1]); // x 不变，那么 y 可以不变，可以减半，取这两种情况的最小值
                halve += p[0]; // x 减半，那么 y 只能不变
                cnt += p[2]; // 自底向上累加差分值
            }
        notHalve += price[x] * cnt; // x 不变
        halve += price[x] * cnt / 2; // x 减半
        return new int[]{notHalve, halve, cnt};
    }
}

作者：endlesscheng
链接：https://leetcode.cn/problems/minimize-the-total-price-of-the-trips/solution/lei-si-da-jia-jie-she-iii-pythonjavacgo-4k3wq/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

337. 打家劫舍 III

难度中等1630

小偷又发现了一个新的可行窃的地区。这个地区只有一个入口，我们称之为 root 。

除了 root 之外，每栋房子有且只有一个“父“房子与之相连。一番侦察之后，聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。如果 两个直接相连的房子在同一天晚上被打劫 ，房屋将自动报警。

给定二叉树的 root 。返回 在不触动警报的情况下 ，小偷能够盗取的最高金额。

示例 1:

输入: root = [3,2,3,null,3,null,1]
输出: 7 
解释: 小偷一晚能够盗取的最高金额 3 + 3 + 1 = 7

示例 2:

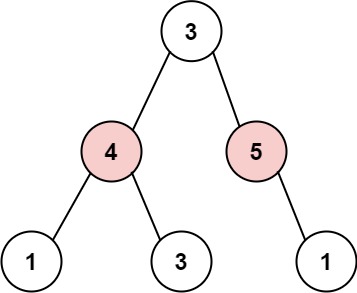
输入: root = [3,4,5,1,3,null,1]
输出: 9
解释: 小偷一晚能够盗取的最高金额 4 + 5 = 9

提示：

树的节点数在 [1, 104] 范围内
0 <= Node.val <= 104

题解：

三种方法解决树形动态规划问题-从入门级代码到高效

作者：reals
链接：https://leetcode.cn/problems/house-robber-iii/solution/san-chong-fang-fa-jie-jue-shu-xing-dong-tai-gui-hu/

说明：本题目本身就是动态规划的树形版本，通过此题解，可以了解一下树形问题在动态规划问题解法

我们通过三个方法不断递进解决问题

解法一通过递归实现，虽然解决了问题，但是复杂度太高
解法二通过解决方法一中的重复子问题，实现了性能的百倍提升
解法三直接省去了重复子问题，性能又提升了一步

解法一、暴力递归 - 最优子结构（超时）

在解法一和解法二中，我们使用爷爷、两个孩子、4 个孙子来说明问题

首先来定义这个问题的状态

爷爷节点获取到最大的偷取的钱数呢

首先要明确相邻的节点不能偷，也就是爷爷选择偷，儿子就不能偷了，但是孙子可以偷

二叉树只有左右两个孩子，一个爷爷最多 2 个儿子，4 个孙子

根据以上条件，我们可以得出单个节点的钱该怎么算

4 个孙子偷的钱 + 爷爷的钱 VS 两个儿子偷的钱哪个组合钱多，就当做当前节点能偷的最大钱数。这就是动态规划里面的最优子结构

由于是二叉树，这里可以选择计算所有子节点

4 个孙子投的钱加上爷爷的钱如下：int method1 = root.val + rob(root.left.left) + rob(root.left.right) + rob(root.right.left) + rob(root.right.right)
两个儿子偷的钱如下：int method2 = rob(root.left) + rob(root.right);

挑选一个钱数多的方案则int result = Math.max(method1, method2);

将上述方案写成代码如下

public int rob(TreeNode root) {
    if (root == null) return 0;

    int money = root.val;
    if (root.left != null) {
        money += (rob(root.left.left) + rob(root.left.right));
    }

    if (root.right != null) {
        money += (rob(root.right.left) + rob(root.right.right));
    }

    return Math.max(money, rob(root.left) + rob(root.right));
}

解法二、记忆化 - 解决重复子问题

针对解法一种速度太慢的问题，经过分析其实现，我们发现爷爷在计算自己能偷多少钱的时候，同时计算了 4 个孙子能偷多少钱，也计算了 2 个儿子能偷多少钱。这样在儿子当爷爷时，就会产生重复计算一遍孙子节点。

于是乎我们发现了一个动态规划的关键优化点：重复子问题

我们这一步针对重复子问题进行优化，我们在做斐波那契数列时，使用的优化方案是记忆化，但是之前的问题都是使用数组解决的，把每次计算的结果都存起来，下次如果再来计算，就从缓存中取，不再计算了，这样就保证每个数字只计算一次。

由于二叉树不适合拿数组当缓存，我们这次使用哈希表来存储结果，TreeNode 当做 key，能偷的钱当做 value

class Solution {
    public int rob(TreeNode root) {
    HashMap<TreeNode, Integer> memo = new HashMap<>();
    return robInternal(root, memo);
	}

 	public int robInternal(TreeNode root, HashMap<TreeNode, Integer> memo) {
 	    if (root == null) return 0;
 	    if (memo.containsKey(root)) return memo.get(root);
 	    int money = root.val;
 	
 	    if (root.left != null) {
 	        money += (robInternal(root.left.left, memo) + robInternal(root.left.right, memo));
 	    }
 	    if (root.right != null) {
 	        money += (robInternal(root.right.left, memo) + robInternal(root.right.right, memo));
 	    }
 	    int result = Math.max(money, robInternal(root.left, memo) + robInternal(root.right, memo));
 	    memo.put(root, result);
 	    return result;
 	}
}

解法三：最优解法

上面两种解法用到了孙子节点，计算爷爷节点能偷的钱还要同时去计算孙子节点投的钱，虽然有了记忆化，但是还是有性能损耗。

我们换一种办法来定义此问题

每个节点可选择偷或者不偷两种状态，根据题目意思，相连节点不能一起偷

当前节点选择偷时，那么两个孩子节点就不能选择偷了
当前节点选择不偷时，两个孩子节点只需要拿最多的钱出来就行(两个孩子节点偷不偷没关系)

我们使用一个大小为 2 的数组来表示 int[] res = new int[2] 0 代表不偷，1 代表偷

任何一个节点能偷到的最大钱的状态可以定义为

**当前节点选择不偷：**当前节点能偷到的最大钱数 = 左孩子能偷到的钱 + 右孩子能偷到的钱
当前节点选择偷：当前节点能偷到的最大钱数 = 左孩子选择自己不偷时能得到的钱 + 右孩子选择不偷时能得到的钱 + 当前节点的钱数

表示为公式如下

root[0] = Math.max(rob(root.left)[0], rob(root.left)[1]) + Math.max(rob(root.right)[0], rob(root.right)[1])
root[1] = rob(root.left)[0] + rob(root.right)[0] + root.val;

将公式做个变换就是代码啦

class Solution {
    /*
    树上最大独立集：
    1. 当前节点 node 要为父节点提供什么信息？
    2. 当前节点 node 能为答案提供什么信息？
    
    x,y
    	x选 += y不选
    	x不选 += max(y选，y不选)
    */
    public int rob(TreeNode root) {
        int[] result = robInternal(root);
        return Math.max(result[0], result[1]);
    }
    // result[] : 0代表不偷， 1代表偷
    public int[] robInternal(TreeNode root){
        if(root == null) return new int[2];
        int[] result = new int[2];
        int[] left = robInternal(root.left);
        int[] right = robInternal(root.right);
        // 当前节点不偷，最大钱数 ： 左孩子能偷到的钱 + 右孩子能偷到的钱
        result[0] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
        // 当前节点偷，最大钱数：左孩子不偷 + 右孩子不偷 + 节点值
        result[1] = left[0] + right[0] + root.val;
        return result;
    }
}

x,y
	x选 += y不选
	x不选 += max(y选，y不选)
*/
public int rob(TreeNode root) {
    int[] result = robInternal(root);
    return Math.max(result[0], result[1]);
}
// result[] : 0代表不偷， 1代表偷
public int[] robInternal(TreeNode root){
    if(root == null) return new int[2];
    int[] result = new int[2];
    int[] left = robInternal(root.left);
    int[] right = robInternal(root.right);
    // 当前节点不偷，最大钱数 ： 左孩子能偷到的钱 + 右孩子能偷到的钱
    result[0] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
    // 当前节点偷，最大钱数：左孩子不偷 + 右孩子不偷 + 节点值
    result[1] = left[0] + right[0] + root.val;
    return result;
}

}