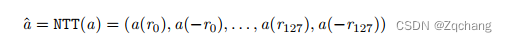提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

反世代距离IGD概念

反世代距离是一个综合性能的评价指标，主要是应用至求解多目标问题中，评价多目标优化算法的综合性能——收敛性、分布性；IGD的值越小，表明算法的收敛性以及分布性越好。
IGD的定义，如下公式所示：

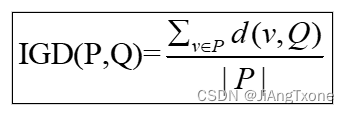
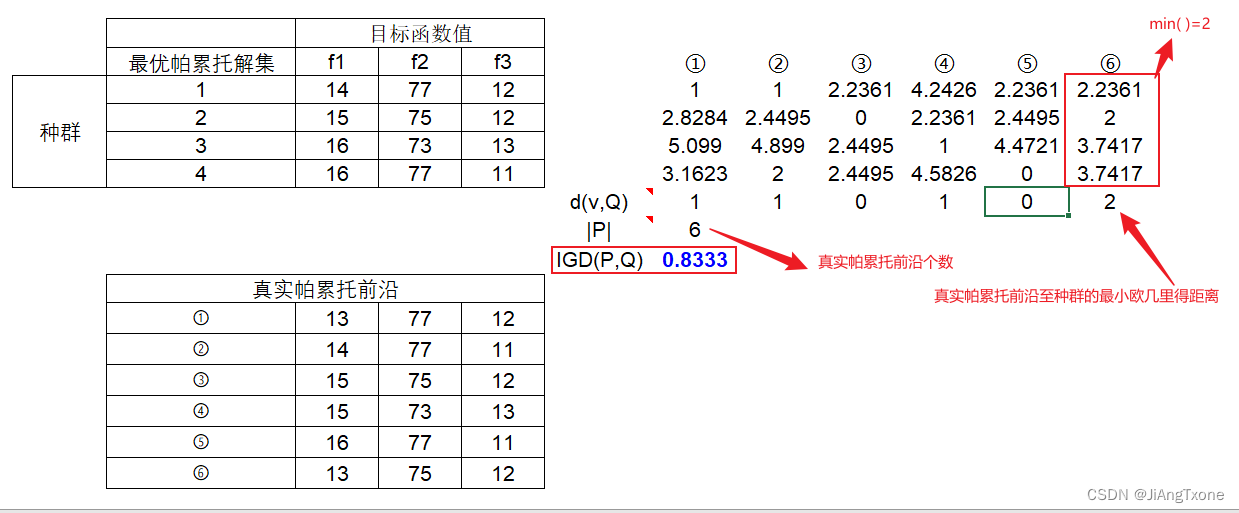
其中，P表示真实的帕累托前沿，Q表示所求解得种群（求解出的最优帕累托解集），d（v，Q）表示P中的个体v到种群Q的最小欧几里得距离，|P|表示分布在帕累托前沿面上点集的个数，IGD是通过计算真实帕累托前沿个体到种群的最小欧几里得距离来评价算法的综合性能。（ps：P真实的帕累托前沿非常多，在计算IGD时，取均匀分布的帕累托前沿即可。）

收敛性能以及分布性能

收敛性能好→d（v，Q）的值相对越小，则IGD的值越小，可评价算法的收敛性能。

若所求解的最优帕累托解集是集中在一个较为狭小的区域，则d（v,Q）的值较大，可通过IGD的值判断算法的分布性能。

举例计算

取6个真实帕累托前沿
真实帕累托前沿

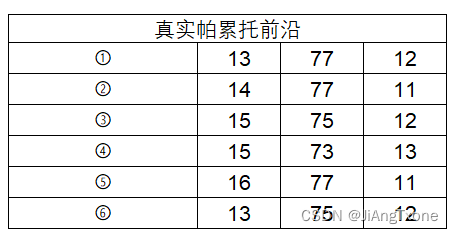
所求解的4个最优帕累托解集

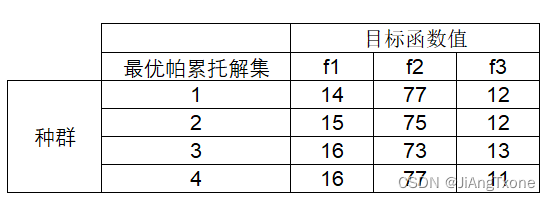
求解反世代距离（IGD）：