简介

CRYSTALS-Dilithium是一种后量子密码学中的数字签名算法。它是由PQClean项目组中的Bernstein、Dahmen、Lange、Nickels和Schneider设计的，并且是NIST PQC竞赛中的一个获胜者。

Dilithium通过使用参数集、哈希函数和多项式函数来进行安全设计。参数集（params）定义了多项式的大小、参数Q（用于压缩表示和NTT域中的数值大小）、参数K（矩阵A中每行的非零系数数）等等。哈希函数用于将消息哈希为要签名的多项式。多项式函数用于执行NTT变换、多项式加法和减法以及其它操作。

CRYSTALS-Dilithium还包括一些安全性和性能保证。它具有强的安全性，能够在处理大量消息时保持高效率。此外，它还包括一些实现指南和支持文档，以帮助在各种应用中正确使用它。

PQClean项目组是一个由密码学家和程序员组成的自愿者团队，致力于实现并标准化后量子密码学算法。该团队的目标是提供经过仔细设计和实现的密码库，以促进后量子时代的安全通信和计算。他们的工作受到了标准化组织NIST的支持和认可，并已成为后量子时代算法的主要参考实现之一。

1和2版本区别

我们首先描述Dilithium的第一轮提交和当前版本之间的区别。我们所做的唯一概念设计更改是允许该方案是随机化的或确定性的选项（而第一轮版本仅为确定性的）。两个版本之间的差异是一行代码，其中一个种子是随机选择的（在随机化版本中），或者作为密钥和消息的哈希值（在确定性版本中）。为了允许确定性和随机化版本之间的这个小差异，函数ExpandMask现在以48字节的种子作为输入，而不是密钥和消息。作为一个小的额外更改，我们还协调了矩阵A，掩蔽向量y和秘密向量s1，s2的各种扩展函数的nonce，使其都为16位整数。

我们对签名算法进行了各种优化，其中最重要的优化是拒绝条件的计算方式，它基于向量w的低位部分和提示向量。我们的AVX2优化实现现在更多地使用向量化，并包括使用宏的简化汇编NTT实现。

此外，我们还引入了一个版本的算法，它使用AES而不是SHAKE来从种子扩展公共矩阵A、秘密向量s1、s2和屏蔽向量y。这主要是为了展示我们的方案在硬件支持SHAKE广泛可用后（如AES一样）的提高效率。

2和3的区别

• 将前两个参数集（使用 4 × 3 和 5 × 4 公钥矩阵）合并为一个 NIST 二级参数集，其中包含一个 4 × 4 公钥矩阵。我们还引入了一个五级参数集。
• 我们现在不总是输出具有60个非零系数（从而具有257位熵）的挑战多项式，而是输出具有39个和49个非零系数的多项式，它们在安全级别2和3中分别具有192和225位熵。这种熵对于相应的安全级别已经足够了（因为在证明中只需要第二前像抵抗），并且具有在一定程度上减少拒绝概率的效果。
• 将公钥中被抛弃的比特数从14降低到13，这会提高该方案的SIS难度，但代价是公钥大小略微增加。
• 现在，遮罩多项式y是从一个范围内进行采样，其中每个系数都有2的幂次方个可能性，这使得采样明显更容易实现。由于之前的范围已经非常接近2的幂次方了，因此这个变化对方案的安全性没有影响。
• 改变了挑战值c的采样和传输方式。现在它采用两个阶段采样。在第一阶段，证明者创建一个哈希值并输出一个32字节的挑战种子 ~c，这就是包含在签名中的。然后使用SHAKE函数以 ~c 作为种子创建签名方案中使用的多项式挑战值。这样可以减小签名的大小，减少了8个字节。
• 这个更新的内容是对方案的安全性分析进行了更新，采用门成本指标，基于近期关于预测格算法行为和成本方面的进展提供了更精细的估计。
• 对 NIST 3 级别的参数集进行了一些小的杂项更改。

1.介绍

我们提出了数字签名方案Dilithium，其安全性基于在格中找到短向量的难度。我们的方案设计考虑以下几个标准：

1. 易于安全实现。最紧凑的基于格的签名方案[DDLL13, DLP14]关键在于需要从离散高斯分布中生成秘密随机数。以安全的方式生成这样的样本非常复杂，很容易导致不安全的实现，如[ BHLY16，EFGT17，PBY17]中所示。虽然可能存在非常谨慎的实现可以防止此类攻击，但假设普遍部署的方案包含许多微妙之处，始终精通地实现是不合理的。因此，Dilithium仅使用均匀采样，正如[Lyu09，GLP12]中最初提出的那样。此外，所有其他操作（例如多项式乘法和舍入）都可以以恒定的时间轻松实现。
2. 谨慎选择参数。因为我们的目标是长期安全，所以我们从攻击者的有利角度分析了格攻击的适用性。特别地，我们考虑了空间需求与时间需求同阶的（量子）算法。目前这样的算法是不现实的，似乎有严重的障碍阻碍了移除空间需求的可能性，但我们允许未来可能会出现改进。
3. 证书链（certificate chain），也称证书路径（certificate path），是一系列数字证书的序列，用于建立数字证书的信任链。每个数字证书都包含公钥和签名，这些签名用于验证其真实性和可信度。证书链由多个数字证书连接在一起，形成一条从根证书到目标证书的路径，每个证书都由下一个证书颁发机构（CA）签名。这个过程一直持续到根证书，根证书由一个受信任的根CA签名，可以被所有信任这个CA的实体信任。证书链的目的是建立数字证书的信任体系，确保数字通信的安全性和可信度。
4. 模块化——变化安全性。几乎构成签名和验证过程全部内容的两个操作是 XOF 扩展（我们使用 SHAKE-128 和 SHAKE-256），以及在多项式环 Zq [X]/(Xn+1) 中的乘法。我们方案高效的实现需要优化这些操作，并确保它们以常数时间运行。对于所有安全级别，我们的方案使用相同的环，其中 q = 223 − 213 + 1，n = 256。变化安全性只是涉及在该环上执行更多/更少的操作，以及执行更多/更少的 XOF 扩展。换句话说，一旦对某个安全级别获得了优化的实现，就很容易获得更高/更低级别的优化实现。

1.1基本方法概述

该方案的设计基于“Fiat-Shamir with Aborts”方法[Lyu09，Lyu12]，与[GLP12，BG14]中提出的方案最相似。对于不熟悉此类签名方案的读者，我们在图1中展示了我们方案的简化（效率较低）版本。该版本是从[BG14]的方案稍作修改得来的。我们将逐个介绍其组成部分，以便读者了解此类方案的工作原理。

没有公钥压缩的签名方案模板

密钥生成算法

生成一个k×l矩阵A，其中每个条目都是环Rq= Zq[X]/(Xn+1)中的多项式。如先前提到的，我们将始终有q = 223−213 +1和n = 256。然后，该算法会对随机密钥向量s1和s2进行采样。这些向量的每个系数都是Rq中具有最多η大小的小系数的元素。最后，公钥的第二部分被计算为t = As1 + s2。这个方案中的所有代数运算都假定在多项式环Rq上进行。

签名过程

签名算法生成一个多项式掩码向量y，其中各系数小于γ1。参数γ1是有策略地设置的，它足够大，使得最终签名不会泄露秘密密钥（即签名算法是零知识的），但也足够小，使得签名不易伪造。然后，签名者计算Ay并将w1设置为此向量中系数的“高阶”位。特别地，Ay中的每个系数w都可以以规范方式写为w = w1·2γ2 + w0，其中|w0|≤γ2；w1是包含所有w1的向量。随后，挑战c被创建为消息和w1的哈希。输出c是一个在Rq中的多项式，恰好有τ个±1和其余为0。之所以采用这种分布，是因为c具有小的范数，并且来自大小为log2 (256 / τ) + τ的域，我们希望其在128和256之间。然后，潜在签名被计算为z = y + cs1。

如果直接输出z，则签名方案将不安全，因为秘密密钥将被泄露。为避免z对秘密密钥的依赖性，我们使用拒绝抽样。参数β设置为csi的最大可能系数。由于c具有τ个±1，而si中的最大系数为η，因此很容易看出β≤τ·η。如果z中的任何系数大于γ1−β，则我们拒绝并重新开始签名过程。此外，如果Az−ct的低阶位的任何系数大于γ2−β，则我们也重新开始。第一个检查对于安全性是必要的，而第二个检查对于安全性和正确性都是必要的。签名过程中的while循环会一直重复，直到满足前两个条件为止。参数被设置得使预期的重复次数不太高（例如大约为4次）。

验证

验证者首先计算$w_1^{{}^{\prime }}$，即Az−ct的高位比特，并且如果z的所有系数都小于γ1−β并且c是消息和$w_1^{{}^{\prime }}$的哈希值，则接受。让我们看看为什么验证可行，特别是为什么HighBits（Az−ct，2γ2）=HighBits（Ay，2γ2）。首先要注意的是Az−ct = Ay−cs2。因此，我们需要证明的是

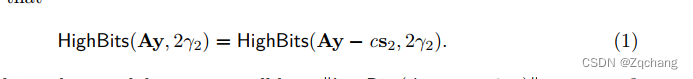
理由是一个有效的签名将有 || LowBits(Ay-cs2, 2γ2) || ∞ < γ2-β。由于我们知道cs2的系数更小，因此我们知道添加cs2不足以通过增加任何低阶系数的幅度至少为γ2来导致任何进位。因此，公式（1）成立，签名可以正确验证。

1.2Dilithium

图1中的基本模板本身相当低效。最明显（但很容易解决）的低效率是，公钥由k·`个多项式的矩阵组成，其表示可能非常大。解决方法是简单地使用SHAKE-128从某些种子ρ生成A，这是一种标准技术。因此，公钥为(ρ, t)，其大小由t主导。Dilithium相对于之前的方案（例如[BG14]和qTESLA[ABB+19]，后者是[BG14]框架的一个特定实例）的新颖之处在于，我们还通过增加不到100字节的签名来缩小了t的位表示大小超过两倍。

获得这种非常有利的权衡的主要观察是，当验证者在第13行计算$w_1^{{}^{\prime }}$时，Az−ct的高位比特不太依赖于t的低位比特，因为t正被一个非常低重量的多项式c乘以。在我们的方案中，t的某些低位比特没有包含在公钥中，因此验证者无法始终正确计算Az−ct的高位比特。为了弥补这一点，签名者在签名中包括了一些“提示”，它们本质上是由于将c与t的缺失低位比特的乘积加入所引起的进位。有了这个提示，验证者就能够正确计算$w_1^{{}^{\prime }}$。

此外，我们提供了一种使用标准技术使我们的方案具有确定性的选项，即将种子添加到密钥中，并使用该种子与消息一起生成 Line 07 中的随机数y。Kiltz等人[KLS18]最近的结果表明，对于相同消息，攻击者看到的不同签名越少，在量子随机预言模型下，签名方案与基础困难假设之间的约束就越紧。虽然目前尚不清楚是否存在针对随机签名的改进量子攻击，但我们建议将确定性版本作为默认选项，除非在攻击者可以利用确定性的侧信道攻击的情况下 [SBB+18, PSS+18]。我们在Fig. 4中的完整方案还利用了基本的优化技巧，如预处理消息M，以避免在每次签名尝试时都重新处理它。

实现注意事项

该方案中进行的主要代数运算是将矩阵A与向量y相乘，其中矩阵A的元素是在Zq[X]/($X^{256}$ + 1)上的多项式，向量y也是如此。在我们的NIST Level 3参数设置中，矩阵A是一个6×5矩阵，因此由30个多项式组成。因此，乘法Ay涉及30个多项式乘法。与许多基于多项式环上运算的基于格的方案一样，我们选择了环，使得乘法操作可以通过数论变换（NTT）实现，这只是一个在有限域Zq上而不是复数上工作的FFT版本。为了启用“完全分裂”NTT算法，我们需要选择一个质数q，使得群Z∗q具有阶数2n = 512;或者等价地，q ≡ 1 (mod 512)。如果r是这样一个元素，则X 256 + 1 = (X−r)(X−$r^3$) ···(X−$r^{511}$)，因此可以等效地将任何多项式a ∈ Zq[X]/($X^{256}$+1)表示为其CRT（中国剩余定理）形式，如(a®,a(r3),… ,a(r2n-1))。这种表示的优点是两个多项式的乘积是按坐标进行的。因此，多项式乘法的最昂贵的部分是变换a →$\hat{a}$和逆变换$\hat{a}$ →a，这些是NTT和逆NTT操作。

以上提到使用NTT表示的优势更加明显，因为在执行矩阵乘法Ay时，需要计算的NTT数量比矩阵的维数少得多。由于矩阵是均匀随机的，因此可以将其生成（并存储）为NTT形式。将向量y∈$R_q^5$转换为NTT表示形式只需要进行5次NTT计算，然后进行逐点乘法计算以获得NTT形式的Ay，最后进行6次逆NTT乘法计算。
另一个耗时的操作是将种子ρ扩展为多项式矩阵A。矩阵A用于签名和验证，因此SHA-KE-128的良好实现对方案的效率很重要。

我们使用整数算术来进行 AVX2 优化的NTT的实现。虽然我们将4个系数打包成一个256位的vector，这与浮点实现使用的密度相同，但我们可以将乘法速度提高约2倍。我们通过仔细安排指令和在NTT期间交错乘法和还原来隐藏部分乘法延迟来实现了这个加速。

安全性。

遵循[Lyu12]的基本方法，可以在随机预言机模型(Random Oracle model, ROM)下证明图1中签名方案的安全性，基于两个问题的难度。第一个问题是标准的LWE(多项式环上)问题，它要求区分(A，t:=As1+s2)和(A，u)，其中u是均匀随机的。另一个问题是[KLS18]中称为SelfTargetMSIS问题，它是找到一个具有小系数的向量$[z，c，v{]}^T$和一个消息(摘要)µ，使得

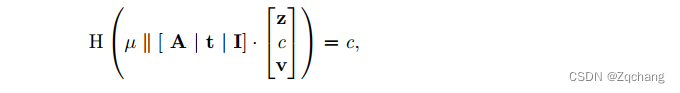
其中 A 和 t 均为均匀随机的矩阵和向量，I 为单位矩阵。在 ROM 中，可以使用分叉引理 [PS00，BN06] 从标准的 MSIS 问题（查找具有满足 Az0 = 0 的小系数的 z0）到 SelfTargetMSIS 中获得（非紧密的）约简。可以按照这个确切的方法，基于 MLWE 和 SIS 的困难性证明 Dilithium 在 ROM 中的安全性。

在量子随机预言机（QROM）模型中，敌手可以在超position中查询H，情况有些不同。在[KLS18]中表明，即使方案是确定性的，Dilithium在QROM中仍基于MLWE和SelfTargetMSIS，即使在密集化情况下也可以进行紧凑约减。但是，我们不能再直接使用分叉引理（因为它是一种类型的回绕）从MSIS到SelfTargetMSIS提供量子约减。仍然有很好的理由相信SelfTargetMSIS问题以及Dilithium在QROM中是安全的。首先，没有使用Fiat-Shamir变换从Σ-协议构建的自然签名方案在ROM中是安全的但在QROM中不是安全的。其次，可以设置Dilithium的参数（同时保持方案设计不变），使得SelfTargetMSIS问题变得信息论上难解，因此仅基于MLWE使该版本的Dilithium在QROM中安全。[KLS18]中的此类参数的实例化导致具有2X签名和5X公钥的方案。虽然我们认为这不是一个很好的权衡，但这种方案的存在使我们对优化的Dilithium的安全性更有信心。

最近，有两项新工作进一步缩小了在ROM和QROM中的安全性差距。[DFMS19]的工作表明，如果底层的Σ-协议是collapsing并具有特殊的soundness性质，则其Fiat-Shamir变换是在QROM中安全的签名。Dilithium Σ-协议的特殊soundness是由MSIS的难度直接导出的[Lyu12，DKL + 18]。此外，[DFMS19]猜测Dilithium Σ-协议是collapsing的。[LZ19]的工作进一步表明，collapsing属性确实具有从MLWE的约简性质。尽管这个约简性质不是特别紧密，但它确实进一步证实了Dilithium的构造或通过Fiat-Shamir框架构建的任何自然方案的本质安全性。在我们看来，证据显然越来越多，即在ROM和QROM中安全的签名之间的区别将很快像在标准模型和ROM中安全的方案之间的区别一样被视为理论上的差异，但实际上安全性将是相同的。

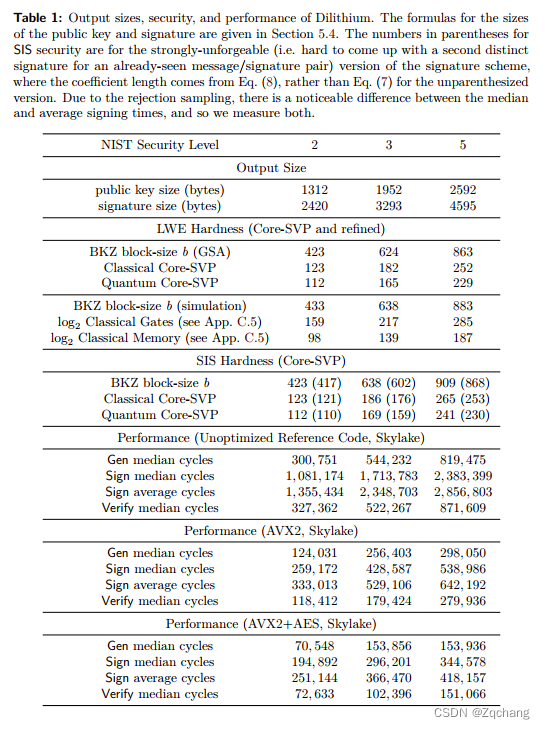
表格1
Dilithium的输出大小、安全性和性能。公钥和签名的大小公式在第5.4节中给出。SIS安全性中括号内的数字是针对强不可伪造（即对于已经见过的消息/签名对难以产生第二个不同的签名）版本的签名方案，其中系数长度来自于方程（8），而非未括号的方程（7）。由于拒绝采样，中位数和平均签名时间之间有明显差异，因此我们两者都进行了测量。

基础操作

环操作

本文中，我们使用 R 和 Rq 表示环 Z[X]/(Xn + 1) 和 Zq[X]/(Xn + 1)，其中 q 是整数，n 的值始终为 256，q 是素数 8380417 = $2^{23}$ − $2^{13}$ + 1。正常字体的字母表示 R 或 Rq 中的元素（包括 Z 和 Zq 中的元素），粗体小写字母表示在 R 或 Rq 中具有系数的列向量。默认情况下，所有向量都是列向量。粗体大写字母表示矩阵。对于向量 v，${\mathbf{v}}^{\mathbf{T}}$ 表示其转置。布尔运算符 statement 的值为 1，如果 statement 为 true，则为 0。

模约简。

对于偶（奇）正整数$\alpha$，我们定义$r_0=r\mathrm{mod}\pm \alpha$为唯一的$r_0$，满足$-\alpha /2<r_0\le \alpha /2$（$-(\alpha -1)/2\le r_0\le (\alpha -1)/2$），例如$r_0\equiv r\mathrm{mod}\alpha$。我们有时将其称为模$\alpha$方的中心约简。对于任何正整数$\alpha$，我们定义$r_0\equiv r\mathrm{mod}\alpha$为唯一的$r_0$，满足$0\le r_0<\alpha$，且$r_0\equiv r\mathrm{mod}\alpha$。当精确表示不重要时，我们简单地写成$r\mathrm{mod}\alpha$。

元素的大小

NTT域表示

我们选择模数q，以便存在一个关于q的512次本原单位根r。具体地，我们始终使用r = 1753。这意味着分圆多项式$X^{256}$ + 1在模q意义下分解为线性因子X − $r_i$（i = 1, 3, 5, …, 511）。根据中国剩余定理，我们的分圆环Rq因此同构于环的乘积$Z_q[X]/(X-r_i)\approx Z_q$。在这个环的乘积中，由于乘法是逐点的，因此易于乘法操作。这个同构关系为：

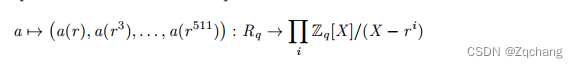
这个同构可以利用快速傅里叶变换快速计算。由于$X^{256}+1=X^{256}-r^{256}=(X^{128}-r^{128})(X^{128}+r^{128})$，因此可以先计算映射：

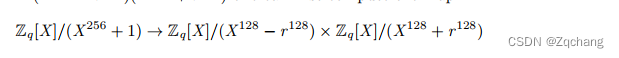
然后单独继续处理度小于128的两个约简多项式，注意到$X^{128}+r^{128}=X^{128}-r^{384}$。在这种情况下，快速傅里叶变换也称为数论变换（NTT），其中地面场是有限场。自然的快速NTT实现不会输出具有按$a(r)$，$a(r^3)$，…，$a(r^{511})$排序的系数的向量。因此，定义NTT域表示a ^ = NTT（a）∈Z_256 q表示多项式a的NTT域表示，其系数按照我们参考NTT的输出排序。

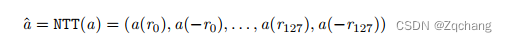
其中ri = $r^{brv(128+i)}$，其中brv(k)是8位数字k的位翻转。使用这种表示法，由于同构属性，我们有ab = NTT−1(NTT(a)NTT(b))。对于向量y和矩阵A，表示yˆ = NTT(y)和Aˆ = NTT(A)表示y和A的每个多项式yi和ai，j都在NTT域表示中。我们在第5.6节中详细介绍了NTT的实现。

2.3 Hashing

signature

Gen

ζ ← { 0 , 1 } 256 \{{0, 1\}}^{256} {0,1}256

ζ 被赋值为一个 256 位的二进制数列，每个元素的取值范围为 {0, 1}。

(ρ, ρ’, K) ∈ { 0 , 1 } 256 \{{0, 1\}}^{256} {0,1}256 × { 0 , 1 } 256 \{{0, 1\}}^{256} {0,1}256 × { 0 , 1 } 256 \{{0, 1\}}^{256} {0,1}256 := H(ζ) H is instantiated as SHAKE-256

这个句子是在描述一个哈希函数 H，它接受一个 256 位的输入 ζ，并输出三个 256 位的二进制数 $\rho$, ${\rho }^{\prime }$, K。其中 $\rho$ 和 ${\rho }^{\prime }$ 是 H 的输出的前两个值，而 K 是 H 的输出的最后一个值。这些值的二进制位是由输入 ζ 和 SHAKE-256 算法共同决定的，因此可以视为是随机生成的。

A ∈ $R_q^{k\times l}$ := ExpandA(ρ) A is generated and stored in NTT Representation as $\hat{A}$

A ∈ $R_q^{k\times l}$ := ExpandA(ρ) 表示生成一个$k\times l$的矩阵A，每个元素都是从$q$的剩余类$R_q$中随机选择的。这里的$R_q$是一个大小为$q$的环，表示在模$q$意义下的所有整数。而ExpandA(ρ)是一个根据输入$\rho$生成矩阵A的函数。在实现中，这个矩阵通常以NTT表示法存储，即矩阵A的每个元素都是模NTT模数的剩余类。因此，我们可以将A表示为$\hat{A}$。

(s1, s2) ∈ $S_{\eta }^l$ × $S_{\eta }^k$ := ExpandS(${\rho }^{\prime }$)

这句话表示一个元组$(s_1,s_2)$属于两个集合，$s_1$属于集合$S_{\eta }^l$，$s_2$属于集合$S_{\eta }^k$。同时这个元组的值是通过将输入参数${\rho }^{\prime }$作为种子，通过某种函数ExpandS生成的。具体来说，$s_1$和$s_2$都是$l$位和$k$位的向量，向量的每个元素都是来自有限集合$-\eta ,\dots ,\eta$中的一个整数。
集合$S_{\eta }^l$是一个有限集合，包含所有$-\eta ,-\eta +1,\cdots ,\eta -1,\eta$中的整数$l$个元素的所有$l$元组。

t := A$s_1$ + $s_2$

这行代码的意思是将矩阵$A$和向量$s_1$做矩阵乘法，再加上向量$s_2$，得到向量$t$。其中，$A$是一个$k\times l$的矩阵，$s_1$是一个$l$维向量，$s_2$是一个$k$维向量，$t$是一个$k$维向量。在这里，我们可以将$A$看作一个公钥，$s_1$和$s_2$看作私钥的一部分，$t$是签名的一部分。

为什么t是签名的一部分

在这个签名方案中，对于给定的消息，签名过程需要使用一组秘密密钥 $(\rho ,{\rho }^{\prime },s)$ 生成一个签名 $(\hat{z},t)$. 其中 $t$ 是与公钥 $A$ 和秘密密钥 $s_1,s_2$ 相关的一个向量，它在签名验证过程中起到关键作用。因此，$t$ 必须作为签名的一部分被包含在内。

($t_1$, $t_0$) := $Power2Roun{d}_q$(t, d)

$(t_1,t_0)$是从向量$t$中获取的。这个向量$t$是由矩阵$A$和向量$s_1,s_2$的线性组合得到的，即$t=A\cdot s_1+s_2$。由于$t$中的元素可能大于$q$，需要将其映射到模$q$的范围内。函数$Power2Roun{d}_q(t,d)$执行了这个映射，并返回了两个向量$t_1$和$t_0$，其中$t_1$的元素都是$q$的$d$次幂的整数倍，而$t_0$的元素是剩余的元素。在这里，$d$是方案参数之一，用于控制这个映射的精度。这个映射可以帮助我们在保证签名安全的同时，减小签名的大小。

tr ∈ { 0 , 1 } 256 \{{0, 1\}}^{256} {0,1}256 := H(ρ || $t_1$)

这段代码的意思是将$(\rho ,t_1)$串接起来，输入到哈希函数$H$中进行哈希运算，得到一个256比特的哈希输出值$tr$。其中，$||$表示将两个比特串连接起来形成一个更长的比特串的操作。

return (pk = (ρ, $t_1$), sk = (ρ, K, tr, $s_1$, $s_2$, $t_0$))

return语句返回了公钥和私钥。其中，公钥pk由元组(ρ, $t_1$)组成，私钥sk由元组(ρ, K, tr, $s_1$, $s_2$, $t_0$)组成。具体来说：

公钥pk中，ρ是哈希函数H的输入，$t_1$是签名的一部分；
私钥sk中，ρ是哈希函数H的输入，K是私钥，tr是另一个哈希函数H’的输出，$s_1$和$s_2$是随机向量，$t_0$是签名的一部分。
在后续的签名和验证过程中，私钥将用于生成签名，公钥将用于验证签名。

签名算法

A ∈ $R_q^{k\times l}$ := ExpandA(ρ) A is generated and stored in NTT Representation as $\hat{A}$

这段代码在Dilithium签名方案的签名算法中表示根据私钥中的$\rho$和公钥中的$l$和$k$，使用密钥扩展算法ExpandA(ρ)生成一个矩阵A，然后对这个矩阵进行NTT变换并存储在NTT表示中，即$\hat{A}$。

μ ∈ { 0 , 1 } 256 : = H ( t r ∣ ∣ M ) \mu \in \{{0, 1\}}^{256} := H(tr\mathbin|\mathbin| M) μ∈{0,1}256:=H(tr∣∣M)

其中 $|$ 表示将两个二进制串拼接起来。这个式子表示将消息 $M$ 和追踪器 $tr$ 一起哈希成一个256比特的二进制串作为 $\mu$ 值。

$\kappa$ = 0，$(z,h)$ = $\perp$

这段代码表示将变量 $\kappa$ 赋值为0，同时将元组 $(z,h)$ 赋值为 $\perp$，表示它们还没有被定义或初始化。

${\rho }^{\prime }$ ∈ { 0 , 1 } 256 \{{0, 1\}}^{256} {0,1}256 := H(K || µ) (or ${\rho }^{\prime }$ ← { 0 , 1 } 256 \{{0, 1\}}^{256} {0,1}256 for randomized signing)

这段代码表示在 Dilithium 签名方案中的密钥生成算法中，${\rho }^{\prime }$ 被赋值为哈希值 H(K || µ) 的结果。其中，K 是一个密钥，µ 是消息的哈希值。如果使用随机签名，则将 ${\rho }^{\prime }$ 随机生成。

while (z, h) = ⊥ do Pre-compute $\widehat{s_1}$ := NTT($s_1$), $\widehat{s_2}$:= NTT($s_2$), and $\widehat{t_0}$ := NTT($t_0$)

这段代码的作用是为了准备一些NTT（Number Theoretic Transform）表示的值，以便后面进行处理。具体来说，$\widehat{s_1}$、$\widehat{s_2}$、$\widehat{t_0}$ 分别是 $s_1$、$s_2$、$t_0$ 的 NTT 表示形式，预先计算这些值可以提高后面的计算效率，因为 NTT 可以加速一些多项式运算。此外，while 循环的条件是 $(z,h)$ 为 ⊥，即当 $(z,h)$ 被赋值后，循环会结束。

y ∈ $S_{{\gamma }_1}^l$ := ExpandMask(${\rho }^{\prime }$, $\kappa$)

表示从 ${\rho }^{\prime }$ 和 $\kappa$ 生成一个长度为 $l$ 的掩码 $y$。在 Dilithium 签名方案中，掩码 $y$ 的作用是用于隐藏签名消息 $m$ 和签名密钥的哈希值 $\mu$，从而防止敌手获取签名者的私密信息。ExpandMask 函数通过将 ${\rho }^{\prime }$ 和 $\kappa$ 哈希后再进行特定计算，得到了掩码 $y$。

w := Ay --------------w := $NT{T}^{-1}(\hat{A}\cdot NTT(y))$

首先，从之前的步骤中，我们获得了展开的密钥 ${\rho }^{\prime }$ 和掩码 $\kappa$。接下来，我们使用 ${\rho }^{\prime }$ 和 $\kappa$ 生成一个向量 $y$，其中 $y$ 属于集合 $S_{{\gamma }_1}^l$，即 $y$ 的每个元素都是 ${\gamma }_1$ 位的整数。

然后，我们使用向量 $y$ 和展开的矩阵 $A$（通过调用 ExpandA(ρ) 函数生成），计算向量 $w$。其中，$A$ 是一个 $k\times l$ 的矩阵，$y$ 是一个 $l$ 维的向量。我们首先将 $y$ 和 $A$ 转换为 NTT 表示形式，然后计算 $\hat{A}\cdot NTT(y)$，最后将结果转换回常规表示形式得到向量 $w$。

因此，这段代码主要用于计算签名中的一个重要部分 $w$。

$w_1$ := $HighBit{s}_q(w,2{\gamma }_2)$

这行代码中的 $HighBit{s}_q$ 函数是指将输入的元素取模 $q$ 之后，只保留最高的 $2{\gamma }_2$ 位，即返回 $w$ 中最高的 $2{\gamma }_2$ 位。其中 ${\gamma }_2$ 是 Dilithium 签名方案中的一个参数，通常取值为 $60$。这个操作的目的是将 $w$ 中的噪声掩码掩盖住，只保留 $w$ 中的有效信息，从而增强签名的安全性。

c ∈ { 0 , 1 } 256 : = H ( κ \{{0, 1\}}^{256} := H(\kappa {0,1}256:=H(κ || w_1)$

这行代码在 Dilithium 签名方案的签名算法中的作用是生成签名中的一个值 $c$。具体来说，该行代码将一个256比特的哈希值赋值给 $c$，其中哈希输入由密钥生成过程中生成的随机值 $\kappa$ 和 $w_1$ 组成。$w_1$ 是 $w$ 的高 $2{\gamma }_2$ 位，$w$ 是由矩阵 $A$ 和掩码 $y$ 计算得出的值，代表了消息的某种哈希。$c$ 是签名中的一个挑战值，用于验证签名的正确性。

c ∈ $B\tau$ := SampleInBall($\hat{c}$) ---- Store c in NTT representation as $\hat{c}$ = NTT( c )

这行代码在Dilithium签名方案的签名算法中，是用来生成签名中的附加噪音项$c$的。其中$B\tau$表示一个球上的离散高斯分布，$\hat{c}$表示$c$在NTT表示中的值。SampleInBall函数会从$B\tau$分布中采样一个随机的$\hat{c}$，并将其转换为$c$的NTT表示$\hat{c}$，最终返回$c$的NTT表示。这个附加噪音$c$对签名的安全性非常重要，可以有效防止攻击者对签名进行反演攻击。

z := y + $c{s}_1$ ------------ Compute c$s_1$ as $NT{T}^{-1}(\hat{c}\cdot \widehat{s_1})$

这行代码在Dilithium签名方案的签名算法中表示计算签名的过程，$z$ 是一个向量，它是随机掩码 $y$ 和校验和 $c{s}_1$ 的和，其中 $c$ 是签名中的一个参数。

$z:=y+c{s}_1$ 表示计算签名中的 $z$ 值，即掩码和。具体来说，${\rho }^{\prime }$ 和 $\kappa$ 由密钥生成算法生成并传递给签名算法，在签名算法中使用 ${\rho }^{\prime }$ 和 $\kappa$ 生成 $y$，并将 $y$ 和签名中的随机数 $s_1$ 组合成 $z$。其中，$c$ 是由 $w_1$ 计算得到的签名哈希值，而 $s_1$ 是由密钥生成算法生成的随机数。最终，使用 $c$ 和 $s_1$ 计算出 $c{s}_1$，并将其加入 $y$ 中，得到 $z$。

$r_0:=LowBit{s}_q(w-c{s}_2,2{\gamma }_2)$ ------------ Compute c$s_1$ as $NT{T}^{-1}(\hat{c}\cdot \widehat{s_1})$

这段代码计算签名$r_0$的值，它是用于保证签名的正确性。具体而言，$r_0$是在$w-c{s}_2$的低$2{\gamma }_2$位上截取的，其中$w$是由公钥$pk$和消息$M$计算出的向量，$c$是签名中的挑战值，$s_2$是密钥中的一个秘密向量。这个截取操作可以确保$r_0$的值在模$q$意义下小于$2{\gamma }_2$，从而符合Dilithium签名方案中的要求。

if $||z|{|}_{\infty }\ge {\gamma }_1$ − β or $||r|{|}_{\infty }\ge {\gamma }_2$ − β, then (z, h) := ⊥

$||z||$ 表示向量 $z$ 的 $L_{\infty }$ 范数，即向量 $z$ 的绝对值最大元素的值。在 Dilithium 签名方案中，$||z||$ 表示 $z$ 向量的 $L_{\infty }$ 范数，通常用于检测 $z$ 是否超过阈值。

向量 $z$ 的 $L_{\infty }$ 范数，也称为最大范数，是指向量 $z$ 的所有元素中绝对值最大的那个元素的值，即：

$||z|{|}_{\infty }={\max }_{1<=i<=n}|z_i|$

其中 $n$ 是向量 $z$ 的长度。

这段代码表示如果向量$z$的各个元素的绝对值超过${\gamma }_1$ - $\beta$ 或者向量$r$的各个元素的绝对值超过${\gamma }_2$ - $\beta$，则将(h, z)设为⊥，重新进行签名过程。其中，${\gamma }_1$和${\gamma }_2$是参数，$\beta$是安全参数。

也就是如果 $z$ 的 $\infty$范数（即绝对值的最大值）大于等于 ${\gamma }_1-\beta$ 或者 $r$ 的 $\infty$-范数大于等于 ${\gamma }_2-\beta$，那么返回 $(z,h):=\perp$ 表示签名失败；

---

else h := $MakeHin{t}_q(-c{t}_0,w-c{s}_2+c{t}_0,2{\gamma }_2$) --------Compute $c{t}_0$ as $NT{T}^{-1}(\hat{c}\cdot \widehat{t_0})$

否则，计算 $c\cdot t_0$ 并存储为 $\widehat{c{t}_0}=NTT(c\cdot t_0)$，然后计算 $h$ 作为一个长度为 $n$ 的向量，其中第 $i$ 位上的值为：

若 $|(-c\cdot t_0{)}_i|<2{\gamma }_2$ 且 $|(w-c{s}_2+c\cdot t_0{)}_i|\ge 2{\gamma }_2$，则 $h_i=1$
若 $|(-c\cdot t_0{)}_i|\ge 2{\gamma }_2$ 且 $|(w-c{s}_2+c\cdot t_0{)}_i|<2{\gamma }_2$，则 $h_i=-1$
否则，$h_i=0$
其中 $w$ 已经是在上一步计算得到的 $w=Ay+z-c{s}_1$，$s_2$ 是在密钥生成阶段计算的，${\gamma }_2$ 是 Dilithium 参数中的一个常数。

在 Dilithium 签名方案中，$MakeHin{t}_q(-c{t}_0,w-c{s}_2+c{t}_0,2{\gamma }_2)$ 函数的作用是生成签名的辅助信息 $h$。该函数将输入的三个向量 $-c{t}_0,w-c{s}_2+c{t}_0$ 和 $2{\gamma }_2$，并输出一个向量 $h$。其中，$-c{t}_0$ 和 $w-c{s}_2+c{t}_0$ 分别是两个 $N$ 元向量，$2{\gamma }_2$ 是一个标量。

生成的 $h$ 在 Dilithium 签名方案中用作签名的一部分，它是一个二元组 $(a,b)$，其中 $a$ 是一个 $\lfloor {\log }_{2}q\rfloor$ 位的整数，$b$ 是一个 $n$ 位的二进制向量。$h$ 的作用是帮助验证人验证签名是否正确。具体地，当签名验证人接收到签名 $(z,h)$、消息 $M$ 和公钥 $pk$ 时，它首先检查 $||z|{|}_{\infty }$ 是否小于 ${\gamma }_1-\beta$，$||r|{|}_{\infty }$ 是否小于 ${\gamma }_2-\beta$，如果是，则认为签名无效，否则它会计算以下值：

$w:=Ay-c{t}_{1}z$
$c^{\prime }:=H(\kappa ||w_1)$
$\widehat{c^{\prime }}:=NTT(c^{\prime })$
$a^{\prime }:=H(\widehat{c^{\prime }}||\hat{z})\mathrm{mod}{2}^{\lfloor {\log }_{2}q\rfloor }$
$b^{\prime }:=MakeHin{t}_q(-a^{\prime }{c}^{\prime }+c{t}_0,w-c{s}_2+c{t}_0,2{\gamma }_2)$
然后，它会检查 $a^{\prime }$ 是否等于 $a$，并使用函数 $UseHin{t}_q(b^{\prime },w-c{s}_2+c{t}_0,2{\gamma }_2)$ 来检查 $c^{\prime }$ 是否等于签名中的 $c$。如果 $a^{\prime }$ 不等于 $a$ 或 $c^{\prime }$ 不等于签名中的 $c$，则验证失败，否则验证成功。因此，$h$ 的作用是帮助验证人在验证签名时计算 $a^{\prime }$ 和 $b^{\prime }$，从而检查签名是否正确

$\kappa$ := $\kappa$ + $l$

在 Dilithium 签名方案中，$\kappa$ 是一个随机种子，它被用于生成一系列的随机数，包括 $y$ 和 $\hat{c}$。每次进行签名时，都需要重新生成这些随机数，因此需要在每次签名之后更新 $\kappa$ 的值，以保证每次生成的随机数都是不同的。在更新 $\kappa$ 的值时，需要将其增加 $l$，因为每次生成的 $y$ 的长度为 $l$，因此每次更新 $\kappa$ 的值都需要增加 $l$。

return σ = ($\hat{c}$, z, h)

这行代码是Dilithium签名算法的输出，返回一个签名 $\sigma$。其中，$\hat{c}$ 是签名中的哈希值的NTT表示，$z$ 是签名中的向量 $y$ 和一些其他值的线性组合，$h$ 是生成签名的过程中计算出的一些用于验证签名的值的哈希值的NTT表示。

验证算法

A ∈ $R_q^{k\times l}$ := ExpandA(ρ)--------- A is generated and stored in NTT Representation as A

在Dilithium验证算法中，矩阵 $A$ 用于计算签名中的向量 $w$。具体地，验证算法需要计算以下两个向量：

$w^{\prime }=A\cdot z-c\cdot t_1$
$w^{\prime \prime }=A\cdot h-c\cdot t_0$
其中 $z$ 和 $h$ 分别是签名中的两个向量，$c$ 是签名中的挑战，$t_1$ 和 $t_0$ 是公钥中的两个向量。由于矩阵 $A$ 存储在 NTT 表示中，因此需要先将向量 $z$ 和 $h$ 转换为 NTT 表示，然后计算 $A$ 和 $t_1$ 的乘积 $A\cdot z$ 和 $c\cdot t_1$ 的乘积，最后通过减法得到向量 $w^{\prime }$。同理，计算 $w^{\prime \prime }$ 也需要用到矩阵 $A$。

μ ∈ { 0 , 1 } 256 : = H ( H ( ρ ∣ ∣ t 1 ) ∣ ∣ M ) \mu \in \{{0, 1\}}^{256} := H(H(\rho |\mathbin|\mathbin t_1)|\mathbin|\mathbin M) μ∈{0,1}256:=H(H(ρ∣∣t1​)∣∣M)

$\rho$ 和 $t_1$ 是签名中的两个参数，M 是待验证的消息，通过这些参数和消息的哈希值，可以计算出签名中的哈希值 $\mu$，用于与签名中的哈希值比对，以判断签名是否正确。

c := SampleInBall($\hat{c}$)

执行 $c:=SampleInBall(\hat{c})$ 表示从半径为 $\beta q$ 的球中均匀随机采样一个向量 $\mathbf{c}$。这里的 $\hat{c}$ 是签名中的 $\hat{c}$，是经过 NTT 变换后的 $\mathbf{c}$。

$w_1^{{}^{\prime }}$ := $UseHin{t}_q(h,Az-c{t}_1\cdot 2^d,2{\gamma }_2)$ ----- Compute as $NT{T}^{-1}(\hat{A}\cdot NTT(z)-NTT(c)\cdot NTT(t_1\cdot 2^d))$

这行代码用于使用前面生成的提示(hint) $h$ 来验证签名。具体来说，首先计算 $Az-c{t}_1\cdot 2^d$ 的 NTT 表示，并使用 $h$ 来提取 $w_1^{{}^{\prime }}$（即 $w$ 的高位）。然后，将 $w_1^{{}^{\prime }}$ 与签名中的 $w_1$ 进行比较，如果它们相等，则验证成功。

return $[[||z|{|}_{\infty }<{\gamma }_1-\beta ]]$ and $[[\hat{c}=H(\mu ||w_1^{{}^{\prime }})]]$ and [[# of 1’s in h is ≤ ω ]]

第一个条件$[[||z|{|}_{\infty }<{\gamma }_1-\beta ]]$检查签名中的$z$向量是否满足限制条件，即$L\infty$范数小于${\gamma }_1-\beta$。如果不满足条件，验证算法返回失败。这个条件保证了签名的正确性和安全性。

第二个条件$[[\hat{c}=H(\mu ||w_1^{{}^{\prime }})]]$检查签名中的$\hat{c}$是否等于通过消息、公钥、和$h$生成的哈希值。如果不满足条件，验证算法返回失败。这个条件保证了签名中的$\hat{c}$值是由正确的信息生成的。

第三个条件[[ # of 1’s in h is ≤ ω} ]] 检查$h$中1的个数是否小于或等于$\omega$。如果$h$中1的个数超过了限制，验证算法返回失败。这个条件保证了签名中的$h$不会太大，从而保证了签名的效率和安全性。