概述

分治法也称为分解法、分治策略等。分治法算法思想如下：

(1) 将一个问题划分为同一类型的若干子问题，子问题最好规模相同。

(2) 对这些子问题求解（一般使用递归方法，但在问题规模足够小时，有时也会利用另一个算法）。

(3) 有必要的话，合并这些子问题的解，以得到原始问题的答案。

当子问题足够大时，需要递归求解时，我们称之为递归情况（Recursive Case）。当子问题变得足够小，不再需要递归时，表示递归已经“触底”，进入了基本情况（Base Case）。

递归式与分治方法紧密相关。因为使用递归式可以很自然地刻画分治算法的运行时间。一个递归式（Recurrence）就是一个等式或不等式，它通过更小的输入上的函数值来描述一个函数。如使用递归式表示归并排序(Merge Sort)的最坏运行时间 T ( n ) T(n) T(n)：

T ( n ) = O ( 1 ) ( n = 1 ) T(n) = O(1) (n=1) T(n)=O(1)(n=1)

T ( n ) = 2 T ( n / 2 ) + O ( n ) ( n > 1 ) T(n) = 2T(n/2) + O(n) (n>1) T(n)=2T(n/2)+O(n)(n>1)

递归与分治

递归的定义：

程序调用自身的编程技巧称为递归。递归做为一种算法在程序设计语言中广泛应用。

一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法，它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解，递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算，大大地减少了程序的代码量。递归的能力在于用有限的语句来定义对象的无限集合。边界条件与递归方程是递归函数的两个要素，递归函数只有具备了这两个要素，才能在有限次计算后得出结果。

例如：计算阶乘

#include<iostream>
using namespace std;
int factorial(int n) {
    if(n==0) return 1;
    else return n*factorial(n-1);
} 
int main(){
    cout<<factorial(5)<<endl;
}

汉诺塔问题

汉诺塔（Tower of Hanoi），又称河内塔，是一个源于印度古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

思路：

1.将n-1个碟子从A杆经C杆移动到B杆 2.将A杆上的第n个碟子移动到C杆 3.将n-1个碟子从B杆经A杆移动到C杆

算法分析

当n=1时 T（n）=1

当n>1时 T（n）=2T(n-1)+1

代码实现

#include <stdio.h>
#include <stdlib.h>
 
static int count = -1;
 
void move(char x,char y);      // 对move函数的声明 
void hanoi(int n,char one,char two,char three) ;//对hanoi函数的声明
int main()
{          
    int m;
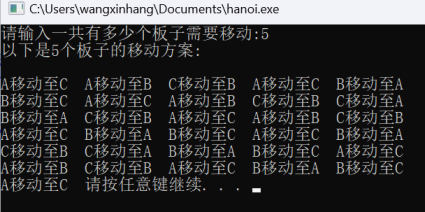
    printf("请输入一共有多少个板子需要移动:");
    scanf("%d",&m);
    printf("以下是%d个板子的移动方案:\n",m);
    hanoi(m,'A','B','C');
    system("pause");
    return 0;
}
 
void hanoi(int n,char one,char two,char three)  // 定义hanoi函数  
// 将n个盘从one座借助two座,移到three座 
{
    
    if(n==1)
        move(one,three);
    else
    {
        hanoi(n-1,one,three,two);  //首先把n-1个从one移动到two
        move(one,three);//然后把最后一个n从one移动到three
        hanoi(n-1,two,one,three); //最后再把n-1个从two移动到three
    }
} 
void move(char x,char y)  //  定义move函数 
{
    count++;
    if( !(count%5) )
        printf("\n");
    printf("%c移动至%c  ",x,y);
}

成果图片

排序问题中的分治法

归并排序

归并排序(Merge Sort)是建立在归并操作上的一种既有效又稳定的排序算法，该算法是采用
分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并，得到完全有序的
序列。即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二
路归并。

步骤

划分：将待排序的序列从中间划分为两个长度相同的子序列

求解子问题：分别对两个子序列进行排序，得到两个有序的子序列

合并：将两个有序子序列合并成一个有序序列

图解

算法

输入：待排序数组r[n],待排序区间[s,t]

输出：升序序列r[s]-r[t]

如果s等于t,则待排序区间只有一个记录,算法结束

计算划分的位置:m=(s+t)/2;

对前半个子序列 r[s]~r[m]进行升序排列;

对后半个子序列 r[m+1]~[t]进行升序排列;

合并两个升序序列 r[s]~r[m]和r[m+1]~r[t];

#include <stdio.h>
#include <iostream>
#include <algorithm>
#include <cstdlib>
#include <cmath>
using namespace std;
void merge(int* a, int low, int mid, int hight)  //合并函数
{
    int* b = new int[hight - low + 1];  //用 new 申请一个辅助函数
    int i = low, j = mid + 1, k = 0;    // k为 b 数组的小标
    while (i <= mid && j <= hight)  
    {
        if (a[i] <= a[j])
        {
            b[k++] = a[i++];  //按从小到大存放在 b 数组里面
        }
        else
        {
            b[k++] = a[j++];
        }
    }
    while (i <= mid)  // j 序列结束，将剩余的 i 序列补充在 b 数组中 
    {
        b[k++] = a[i++];
    }
    while (j <= hight)// i 序列结束，将剩余的 j 序列补充在 b 数组中 
    {
        b[k++] = a[j++];
    }
    k = 0;  //从小标为 0 开始传送
    for (int i = low; i <= hight; i++)  //将 b 数组的值传递给数组 a
    {
        a[i] = b[k++];
    }
    delete[]b;     // 辅助数组用完后，将其的空间进行释放（销毁）
}
void mergesort(int* a, int low, int hight) //归并排序
{
    if (low < hight)
    {
        int mid = (low + hight) / 2;
        mergesort(a, low, mid);          //对 a[low,mid]进行排序
        mergesort(a, mid + 1, hight);    //对 a[mid+1,hight]进行排序
        merge(a, low, mid, hight);       //进行合并操作
    }
}
int main()
{
    int n, a[100];
    cout << "请输入数列中的元素个数 n 为：" << endl;
    cin >> n;
    cout << "请依次输入数列中的元素：" << endl;
    for (int i = 0; i < n; i++)
    {
        cin >> a[i];
    }
    mergesort(a, 0, n-1);
    cout << "归并排序结果" << endl;
    for (int i = 0; i < n; i++)
    {
        cout << a[i] << " ";
    }
    cout << endl;
    return 0;
}

快速排序

快速排序是对冒泡排序的一种改进。基本思想是：通过一趟排序将待排记录分割成独立的两部分，其中一部分记录的关键字均比另一部分记录的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序。

首先用数组的第一个数作为枢轴，然后将所有比它小的数都放到它的位置之前，所有比它大的数都放到它的位置之后，由此可以该“枢轴“记录最后所落的位置i作为分界线，将序列分割成两个子序列。这个过程称为一趟快速排序。

步骤

划分：选定一个记录作为轴值，以轴值为基准将整个序列分为两个子序列，左侧数小于轴值，右侧大于

求解子问题：对每一个子序列进行递归处理

合并：对于子序列的排序是就地进行，不需要任何操作

代码

void quickSort(int left, int right, vector<int>& arr)
{
    if(left >= right)
        return;
    int i, j, base, temp;
    i = left, j = right;
    base = arr[left];  //取最左边的数为基准数
    while (i < j)
    {
        while (arr[j] >= base && i < j)
            j--;
        while (arr[i] <= base && i < j)
            i++;
        if(i < j)
        {
            temp = arr[i];
            arr[i] = arr[j];
            arr[j] = temp;
        }
    }
    //基准数归位
    arr[left] = arr[i];
    arr[i] = base;
    quickSort(left, i - 1, arr);//递归左边
    quickSort(i + 1, right, arr);//递归右边
}