1. 根号分治

哈希冲突

题目1

$n$ 个数，$m$ 次操作。操作 1 为修改某一个数的值，操作 2 为查询所有满足下标模 $x$ 等于 $y$ 的数之和。

先来看两个暴力算法：

• 算法 1：

  修改：直接修改。时间复杂度 $O(1)$ 。
  查询：枚举下标模 $x$ 等于 $y$ 的数的和。时间复杂度 $O(n)$ 。

• 算法 2：

  先预处理出 $f(i,j)$ 表示下标模 $i$ 等于 $j$ 的数之和。时间复杂度 $O(n^2)$ 。
  修改：修改所有 $i$ 下的 $f(i,x\mathrm{mod}i)$。时间复杂度 $O(n)$
  查询：直接查询。时间复杂度 $O(1)$。

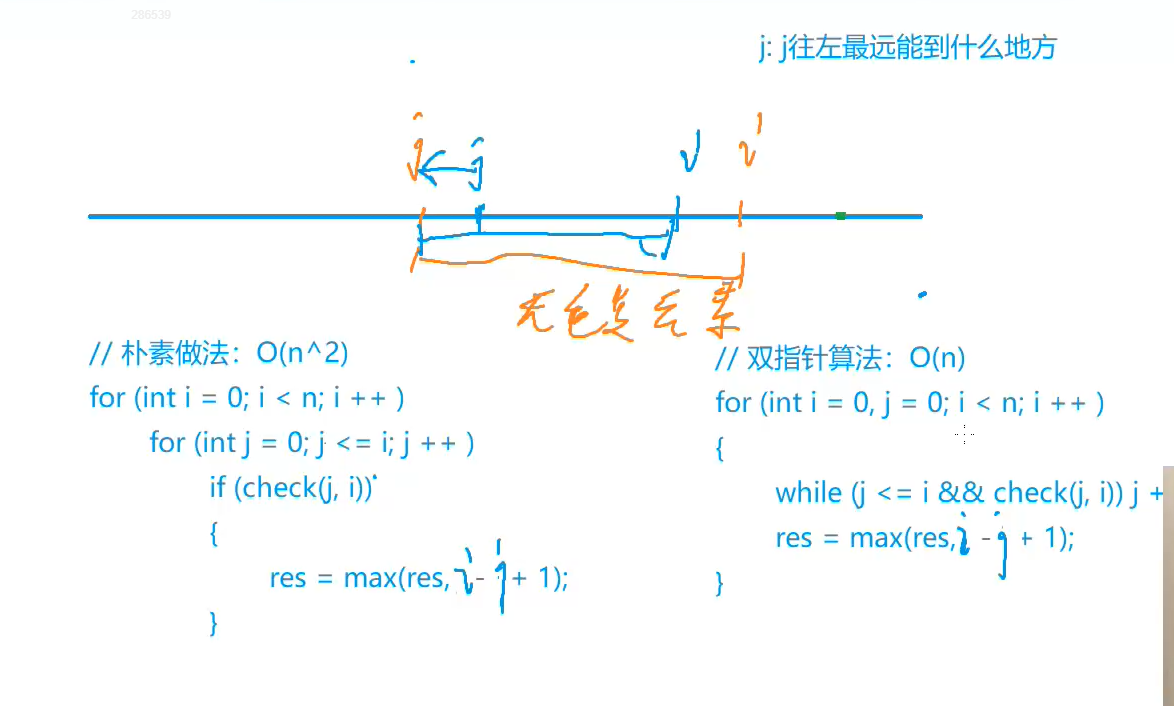
容易想到划定一个界限 $B$ 选择使用的算法。

当 $x$ 较大时，即 $x>B$ 时，算法 1 的查询次数会较小，复杂度 $O(\frac{N}{B})$ 。

当我们仅用算法 2 处理模数 $i$ 较小的情况时，即 $i\le B$ 时，算法 2 复杂度会较低，预处理复杂度 $O(B^2)$，修改复杂度 $O(B)$。

总时间复杂度 $O(B^2+m(\frac{N}{B}+B))$。在 $B=\sqrt{N}$ 时复杂度最低。

代码

---

2. 线性分块

引入

题目

给定 $n$ 个数 $a[\mathrm{1..}n]$，$m$ 次操作，区间修改，区间查询。

我们将数列分段，设块长为 $B$。

对于区间 $[L,R]$ 的询问：

• 若 $L,R$ 在同一个块内，直接暴力枚举 $[L,R]$ 统计。

• 若 $L,R$ 不在同一个块内，则将 $[L,R]$ 分成左右两个散块以及中间若干整块。对于每个整块，我们事先预处理出每个整块的 $b_i=\sum a_i$。对于散块，暴力统计。

  时间复杂度至多 $O(B+\frac{N}{B})$ 。

对于区间 $[L,R]$ 的修改：

• 若 $L,R$ 在同一个块内，直接暴力枚举 $[L,R]$ 修改。

• 若 $L,R$ 不在同一个块内，则将 $[L,R]$ 分成左右两个散块以及中间若干整块。对于每个整块，我们修改整块的 $b_i$。对于散块，暴力修改。

  时间复杂度至多 $O(B+\frac{N}{B})$ 。

$B=\sqrt{N}$ 时最优。

代码

---

教主的魔法

题目

给定 $n$ 个数，$m$ 次操作。区间修改，区间查询有多少个数 $\ge k$。

设块长为 $B$。

• 对于区间 $[L,R]$ 的询问：

  与上题基本一样，但是我们需要快速统计出整块中有多少个 $\ge k$ 的数。考虑将所有整块内元素排序后二分查找。

  时间复杂度至多 $O(B+\frac{N}{B}\log B)$ 。

• 对于区间 $[L,R]$ 的修改：

  修改整块并不会改变排序后的相对位置，记录标记表示增加的量即可。

  而对于散块的修改，可能会改变所在块的相对位置，我们暴力修改后重新排序。

  时间复杂度至多 $O(B+\log B+\frac{N}{B})$ 。

复杂度最低时，$B$ 的大小应该为 $\sqrt{N}$ 左右（略大于 $\sqrt{N}$，取 $\sqrt{N}$ 也能过）。

代码

同类题 ：Array Transformer (附代码)

---

[CQOI2011] 动态逆序对

题目

给定 $n$ 个数的一个排列，$m$ 此操作。每次删一个数，问删前逆序对个数。

删除一个数后，逆序对数量会减少这个数的贡献。第 $i$ 个数的贡献为 $[1,i)$ 中比 $i$ 大的个数加上 $(i,n]$ 中比 $i$ 小的个数。和上一题类似，可以用二分或者树状数组解决。

代码

---

[国家集训队] 排队

题目

给定 $n$ 个数 $h_1...h_n$ ，$m$ 次操作。每次操作交换两个数，问操作前的逆序对个数。

和上一题一样，考虑两个数交换前和交换后的贡献。

代码

双倍经验 ：Anton and Permutation (附代码)

---

[HNOI2010] 弹飞绵羊

题目

题意见题面。

考虑预处理出 $step[x]$ 表示从 $x$ 处开始弹几步能弹到下一块，$pos[x]$ 表示从 $x$ 开始第一次弹到下一块的位置在哪里。

查询：每次跳到下一块，复杂度为 $O(\frac{N}{B})$ 。
修改：记修改点为 $x$ ，所在块为 $B$ ，块对应区间为 $[L_B,R_B]$ ，那么可能会对 $[L_B,x]$ 上的点的 $pos$ 和 $step$ 造成影响。复杂度 $O(B)$。

$B=\sqrt{N}$ 。

代码

双倍经验 ：Holes (附代码)

---

蒲公英

题目

静态求区间众数，强制在线。

分析：

• $n\le 4\times 10^4,a\le 10^9$ ，考虑离散化。

• 由于众数不满足一些性质（如可加性等），无法方便的用一些数据结构维护出来，考虑分块。

Solution

我们将序列分成 $K$ 段，每段长度 $\frac{N}{K}$ （左右）。

对于一次询问 $[l,r]$ ，将其划分为若干整块和两块散块：

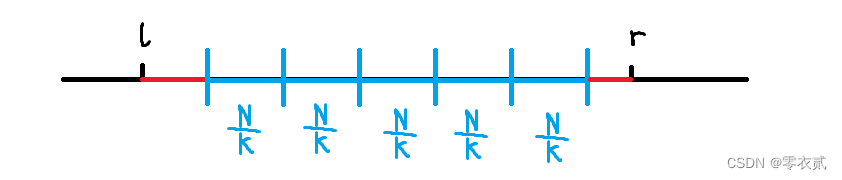
那么，答案一定为蓝色区间的众数或者红色区间出现过的数字。

考虑预处理出任意 $i$ 到 $j$ 块间的众数，来快速求出蓝色区间的众数，预处理时间复杂度 $O(K^{2}N)$。

// cnt[i][j][x] : x 在 i 到 j 块间出现的次数
// num[i][j] : i 到 j 块间的众数
	for(int i=1; i<=n; i++)
    {
        int B = ceil((1.0 * i) / (1.0 * len));
        belong[i] = B;
        cnt[B][B][a[i]] ++ ;
    }
	
	for(int i=1; i<=n; i++)
	{
		int B = ceil((1.0 * i) / (1.0 * len));
        if(cnt[B][B][a[i]] == cnt[B][B][num[B][B]] && a[i] < num[B][B]) num[B][B] = a[i];
        if(cnt[B][B][a[i]] > cnt[B][B][num[B][B]]) num[B][B] = a[i];
	}
	
    for(int i=1; i<=k; i++)
        for(int j=i+1; j<=k; j++)
            for(int x=1; x<=tot; x++)
            {
                cnt[i][j][x] = cnt[i][j-1][x] + cnt[j][j][x];
                if(cnt[i][j][x] == cnt[i][j][num[i][j]] && x < num[i][j]) num[i][j] = x;
                if(cnt[i][j][x] > cnt[i][j][num[i][j]]) num[i][j] = x;
            }
    

对于每次询问，我们 $O(1)$ 求蓝色区间的众数，$O(\frac{N}{K})$ 枚举红色区间的数，计算 $[l,r]$ 的众数，询问时间复杂度 $O(M\frac{N}{K})$。

总时间复杂度 $O(N{K}^2+M\frac{N}{K})$，如果我们认为 $N,M$ 同构，那么 $K=N^{\frac{1}{3}}$ 时复杂度最低。

代码

---