---

一、题目描述

给你二叉树的根结点 root ，请你将它展开为一个单链表：

展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
展开后的单链表应该与二叉树 先序遍历 顺序相同。

示例 1

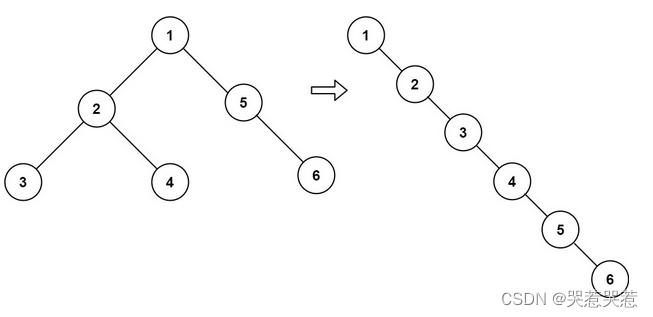
输入：root = [1,2,5,3,4,null,6]
输出：[1,null,2,null,3,null,4,null,5,null,6]

示例 2

输入：root = []
输出：[]

示例 3

输入：root = [0]
输出：[0]

提示：
树中结点数在范围 [0, 2000] 内
-100 <= Node.val <= 100

二、代码

代码如下：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def flatten(self, root: Optional[TreeNode]) -> None:
        """
        Do not return anything, modify root in-place instead.
        """
        def preoder(root,path):
            path.append(root.val)
            if root.left:
                preoder(root.left,path)
            if root.right:
                preoder(root.right,path)
        preorder_path = []
        def ConstructBT(root):
            if preorder_path:
                if root.right:
                    root.right.val = preorder_path.pop(0)
                else:
                    root.right = TreeNode(preorder_path.pop(0))
                if root.left:
                    root.left = None
                ConstructBT(root.right)
        if root:
            preoder(root,preorder_path)
            print(preorder_path)
            root.val = preorder_path.pop(0)
            ConstructBT(root)
            print(root)

---

三、解题思路

本题基于二叉树的先序遍历，将遍历结果按顺序重新构造一个“单链表”，实际上是一个没有左子树的二叉树。
本题直接在原本的root上进行修改，解题思路如下：
①遍历二叉树找到其先序遍历序列preorder_path，其中preorder_path中每个值为二叉树结点的值。
②重新构造二叉树；使用ConstructBT(root)方法依次修改已知二叉树root的每一个节点，具体操作有3步：1）当前节点原本就存在其右子树，则直接修改右子树的值；2）如果当前节点不存在右子树，则为其添加一个新的右子树节点；3）如果当前节点存在左子树，则令左子树为空。
将先序遍历序列preorder_path中的值都添加或修改进二叉树root后，返回当前root即可。