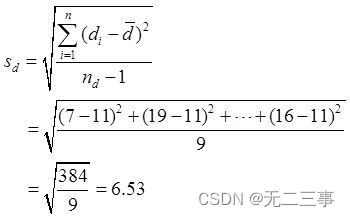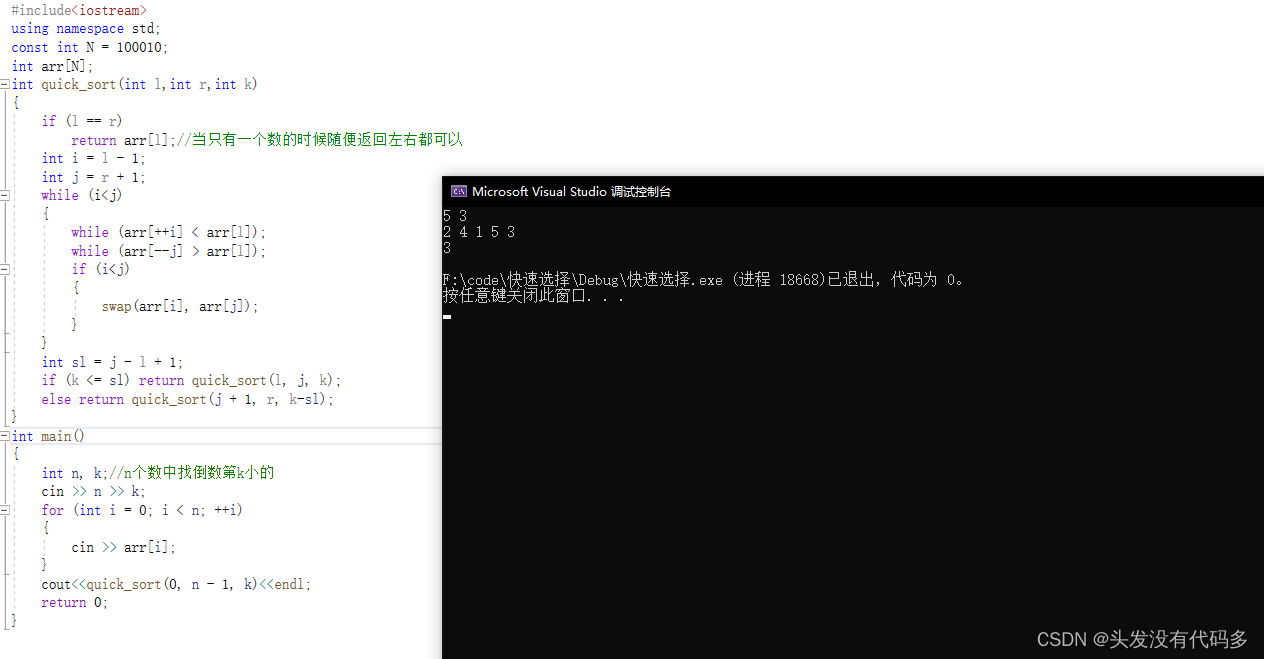
求第K个数

思路：用快速选择，时间复杂度为O(N)

sl和sr是左边和右边数的个数，当k<=sl，即倒数第K个数在左边范围内，递归左边，反之，递归右边,递归右边的时候k传参时要变为k-sl，因为递归时候已经排好序，在整体中是找第k个小的，但对于右边的单独数组来说，是找k-sl位置的（这里按从小到大的排序）

#include<iostream>
using namespace std;
const int N = 100010;
int arr[N];
int quick_sort(int l,int r,int k)
{
	if (l == r)
		return arr[l];//当只有一个数的时候随便返回左右都可以
	int i = l - 1;
	int j = r + 1;
	while (i<j)
	{
		while (arr[++i] < arr[l]);
		while (arr[--j] > arr[l]);
		if (i<j)
		{
			swap(arr[i], arr[j]);
		}
	}
	int sl = j - l + 1;
	if (k <= sl) return quick_sort(l, j, k);
	else return quick_sort(j + 1, r, k-sl);
}
int main()
{
	int n, k;//n个数中找倒数第k小的
	cin >> n >> k;
	for (int i = 0; i < n; ++i)
	{
		cin >> arr[i];
	}
	cout<<quick_sort(0, n - 1, k)<<endl;
	return 0;
}

求逆序对的数量

如从5 3 2 1 4中随机选俩个数，选的第一个数>第二个数，则这对数字称为逆序对

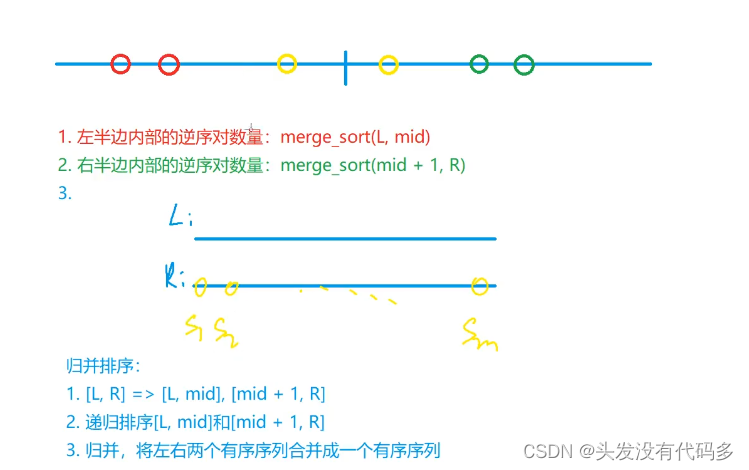
分为三种情况：左左，右右，一左一右

第三种情况（一左一右）：我们在左边找比右边第一个大的数字，结果记为s1,若右边有m个数，则总共有s1+s2+s3......+sm个逆序对

s1和s2.....sm如何计算？

由于我们是用递归的方法将数组有序化的，如要找比下标为j大的数，我们只需找到第一个比它大的数即可，下标记作i，这样i一直到结尾的数字都比j大（因为我们拍好了序），只需计算出左边最后一个数字到i的个数即可

sj计算思路，由于上面的数组最左边是mid，则i到mid的数总共是mid-i+1个

若有n个数字，从大到小排列，如n,n-1,n-2,n-3......1，逆序对的数量为n(n-1)/2对，下题把n=100000带进去。

#include<iostream>
using namespace std;
typedef long long LL;
const int N = 100010;
int arr[N],temp[N];
LL merge_sort(int l, int r)
{
	if (l >= r)
		return 0;
	int mid = (l + r) / 2;
	LL res = merge_sort(l, mid) + merge_sort(mid + 1, r);
	int i = l,j=mid+1,k=0;
	while (i <= mid && j <= r)
	{
		if (arr[i] < arr[j])
			temp[k++] = arr[i++];
		else
		{
			temp[k++] = arr[j++];
			res = mid - i + 1;
		}
	}
	while (i <= mid) temp[k++] = arr[i++];
	while (j <= r) temp[k++] = arr[j++];
	for (int i = l, j = 0; i <= r; i++, j++)//把数组恢复
		arr[i] = temp[j];
	return res;
}
int main()
{
	int n;
	cin >> n;
	for (int i = 0; i < n; ++i)
		cin >> arr[i];
	cout<<merge_sort(0, n - 1)<<endl;
	return 0;
}

数的三次方根

中间值为m，m³数学符号≥x，就说明m>=三次根号下x，即三次根号下x在m的左半边，我们把整个区间更新成左区间即可（左端点不动，右端点为m）。反之，更新右端点。

这里要保留六位小数，为保险起见，我们再多保留俩位，即保留8为，这种题，一般都会选择多保留俩位小数。

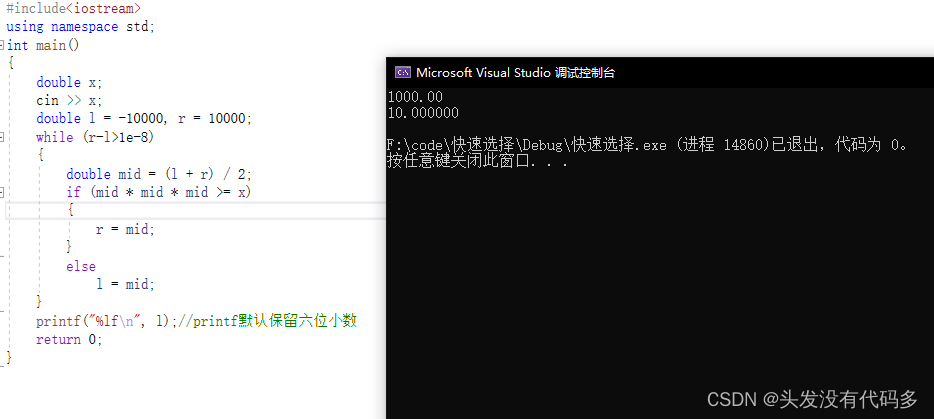
#include<iostream>
using namespace std;
int main()
{
	double x;
	cin >> x;
	double l = -10000, r = 10000;
	while (r-l>1e-8)
	{
		double mid = (l + r) / 2;
		if (mid * mid * mid >= x)
		{
			r = mid;
		}
		else
			l = mid;
	}
	printf("%lf\n", l);//printf默认保留六位小数
	return 0;
}

一维前缀和

#include<iostream>
using namespace std;
const int N = 100010;
int arr[N], s[N];
int main()
{
	int n, m;
	cin >> n >> m;
	for (int i = 1; i <= n; ++i)
		cin >> arr[i];
	for (int i = 1; i <= n; ++i)
		s[i] = s[i - 1] + arr[i];
	int l, r;
	while (m--)
	{
		cin >> l >> r;
		cout << s[r] - s[l - 1] << endl;
	}
	return 0;
}

二维前缀和（子矩阵的和）

#include<iostream>
using namespace std;
const int N = 1010;
int main()
{
	int n, m, q;
	scanf("%d%d%d", &n, &m, &q);//确定二维数组大小
	int arr1[N][N];
	int s[N][N];
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= m; j++)
		{
			scanf("%d", &arr1[i][j]);
		}
	}
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= m; j++)
		{
			s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + arr1[i][j];//某点的区域面积，确定大区域
		}
	}
	while (q--)
	{
		int x1, x2, y1, y2;//某个特定的小区域（在大区域中的小区域）
		scanf("%d%d%d%d", &x1, &y1, &x2, &y2);//x2,y2是最右边的点
		printf("%d\n", s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);
	}
	return 0;
}