浮点数

  浮点数。当机器字长为n时，定点数的补码和移码可表示2的n方个数，而其原码和反码只能表示2"-1个数（0的表示占用了两个编码)，因此，定点数所能表示的数值范围比较小，在运算中很容易因结果超出范围而溢出。浮点数是小数点位置不固定的数，它能表示更大范围的数。
  在十进制中，一个数可以写成多种表示形式。例如，83.125可写成10的3次方× 0.083125或10的4次方×0.0083125等。同样，一个二进制数也可以写成多种表示形式。由此可知，一个二进制数N可以表示为更一般的形式N=2的E次方×F，其中E称为阶码，F称为尾数。用阶码和尾数表示的数称为浮点数，这种表示数的方法称为浮点表示法。
  在浮点表示法中，阶码为带符号的纯整数，尾数为带符号的纯小数。浮点数的表示格式如下:

  很明显，一个数的浮点表示不是唯一的。当小数点的位置改变时，阶码也随着相应改变，因此可以用多个浮点形式表示同一个数。
  浮点数所能表示的数值范围主要由阶码决定，所表示数值的精度则由尾数决定。为了充分利用尾数来表示更多的有效数字，通常采用规格化浮点数。规格化就是将尾数的绝对值限定在区间[0.5,1]。
  如果浮点数的阶码（包括1位阶符）用R位的移码表示，尾数（包括1位数符）用M位的补码表示，则这种浮点数所能表示的数值范围如下：

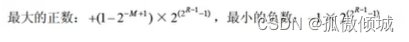
练习：

答案 B
解析