Transformer在时序预测的应⽤第一弹——Autoformer

原文地址：Autoformer: Decomposition Transformers with Auto-Correlation for Long-Term Series Forecasting（NIPS 2021）

做长时间序列的预测
Decomposition把时间序列做拆分，分解
提出新的注意力机制Auto-Correlation

Abstract

该论文提出了一种名为Autoformer的新深度学习模型，用于对时间序列数据进行长期预测。它使用具有自动关联机制的分解架构来发现和表示子系列级别的依赖关系，从而在涵盖实际应用的六个基准测试上具有最高的准确性。

Introduction

在导言中，作者强调了长期预测对于诸如天气预报和能耗规划等实际应用的重要性。他们指出，尽管基于Transformer的模型在发现时间序列数据中的长期依赖关系方面显示出前景，但在处理复杂的时间模式和有效利用长序列信息方面，他们面临着挑战。为了应对这些挑战，作者提出了一个名为Autoformer的新模型，该模型使用分解架构和自相关机制来发现和表示子系列级别的依赖关系。它们在涵盖实际应用的六个基准测试中展示了Autoformer的有效性。

Contributions

1. 提出一种名为Autoformer的新深度学习模型，用于对时间序列数据进行长期预测。
2. 引入具有自相关机制的分解架构，用于在子系列级别发现和表示依赖关系。
3. 在涵盖实际应用的六个基准测试上展示Autoformer的有效性，实现了最先进的精度，比现有方法相对提高了38％。
4. 深入了解基于 Transformer 的现有模型在处理复杂的时间模式和有效利用长序列信息方面的局限性。

practical implications

本文的实际意义对于需要长期预测时间序列数据的各个领域都具有重要意义，例如天气预报、能耗规划、交通预测和疾病爆发监测。所提出的具有自相关机制的Autoformer模型可以提高长期预测的准确性，从而在这些领域做出更好的决策和规划。Autoformer 的分解架构还可以帮助理解时间序列数据中的底层模式和依赖关系，这对于进一步的分析和解释很有用。总体而言，本文为提高时间序列数据长期预测的准确性和效率提供了一种有前途的方法。

Method

本文中使用的方法是：

1。提出一种名为Autoformer的新深度学习模型，用于对时间序列数据进行长期预测。
2。引入具有自相关机制的分解架构，用于在子系列级别发现和表示依赖关系。
3。在涵盖能源、交通、经济、天气和疾病等实际应用的六个基准上进行实验，以评估 Autoformer 的有效性。
4。将 Autoformer 的性能与现有的最先进方法（包括基于 Transformer 的模型）进行比较，并证明精度有了显著提高。
5。深入了解基于 Transformer 的现有模型在处理复杂的时间模式和有效利用长序列信息方面的局限性。

Data

该论文使用了涵盖能源、交通、经济、天气和疾病等实际应用的六个基准数据集来评估拟议的Autoformer模型的有效性。本文中使用的具体数据集未提及。

Future works

建议未来的工作，例如探索Autoformer在其他时间序列应用中的潜力，研究模型的可解释性，以及提高自相关机制的效率。

Limitations

该论文没有明确提及任何限制。但是，一个潜在的局限性可能是拟议的Autoformer模型可能不适用于所有类型的时间序列数据，需要进一步研究以探索其可推广到其他领域。此外，该论文没有详细分析拟议模型的计算复杂性，这可能是大规模应用的问题。

Conclusions

该论文提出了一种名为Autoformer的新型深度学习模型，用于长期预测时间序列数据。提出的模型使用具有自相关机制的分解架构来发现和表示子系列级别的依赖关系。该论文表明，在准确性和效率方面，Autoformer 的性能优于现有的最先进方法，包括基于变压器的模型。在涵盖能源、交通、经济、天气和疾病等实际应用的六个基准数据集上进行的实验表明，与现有方法相比，Autoformer在准确性方面取得了显著改善。本文深入探讨了基于Transformer的现有模型在处理复杂的时间模式和有效利用长序列信息方面的局限性。拟议的Autoformer模型有可能应用于其他时间序列应用，未来的研究可能会探索其可推广到其他领域。

Autoformer是Transformer的升级版本，针对时间序列问题的特性对原始Transformer进⾏了⼀系列优化。模型的整体结构如下图，核⼼是Series Decomposition Block模块和对多头注意⼒机制的升级AutoCorrelationMechanism。这⾥推荐想详细了解Autoformer细节的同学参考杰少的这篇⽂章：，整理的⾮常全⾯深⼊。下⾯给⼤家简单介绍⼀下Auroformer的各个模块。

随机变量独立分布不会受别的变量影响，最小原则

离散型

时间序列的拆分

为了解决时间特征和突破计算效率的瓶颈

举了两个例子
1.季节性拆分
2.矩阵拆分·

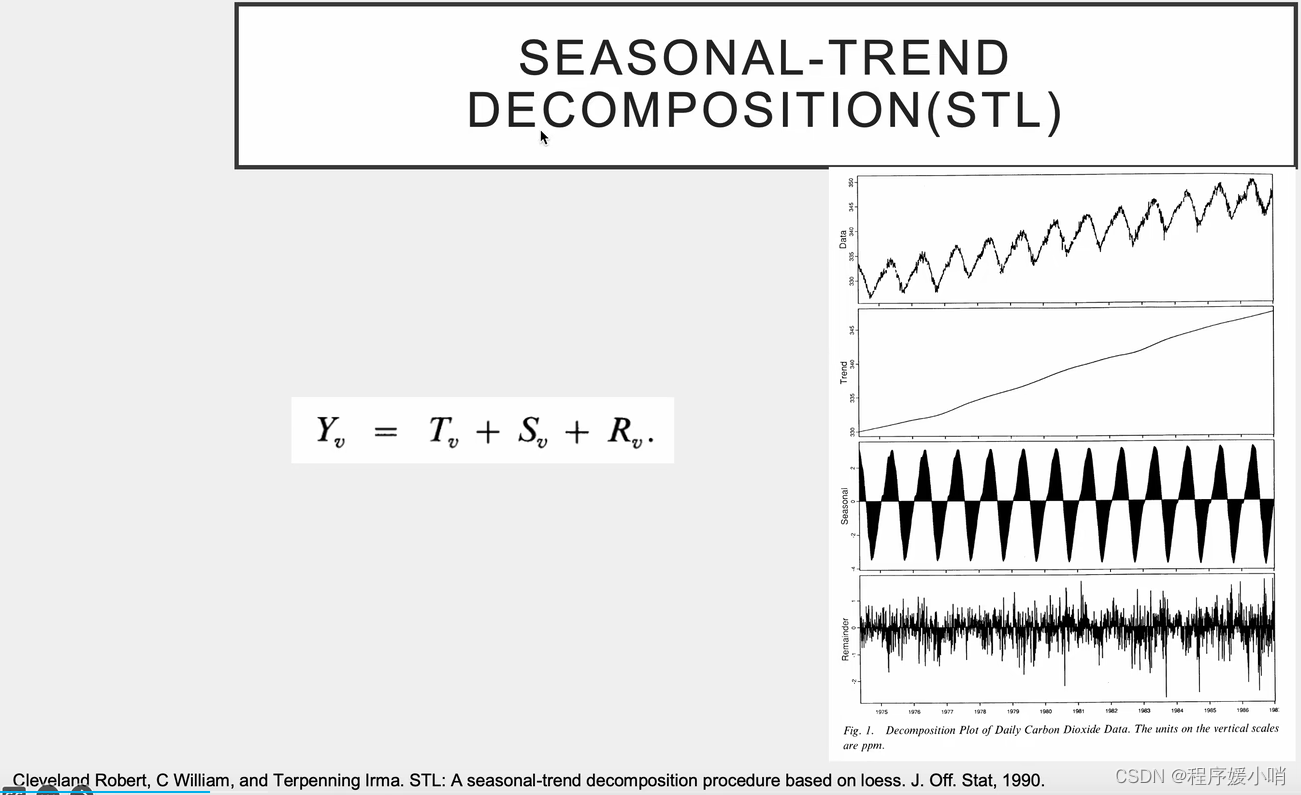
数据（1震荡）=趋势性（2不震荡）+季节性（3提交震荡性）+余项（以0为均值非常不规律的数，原始数据-2-3）

Framework

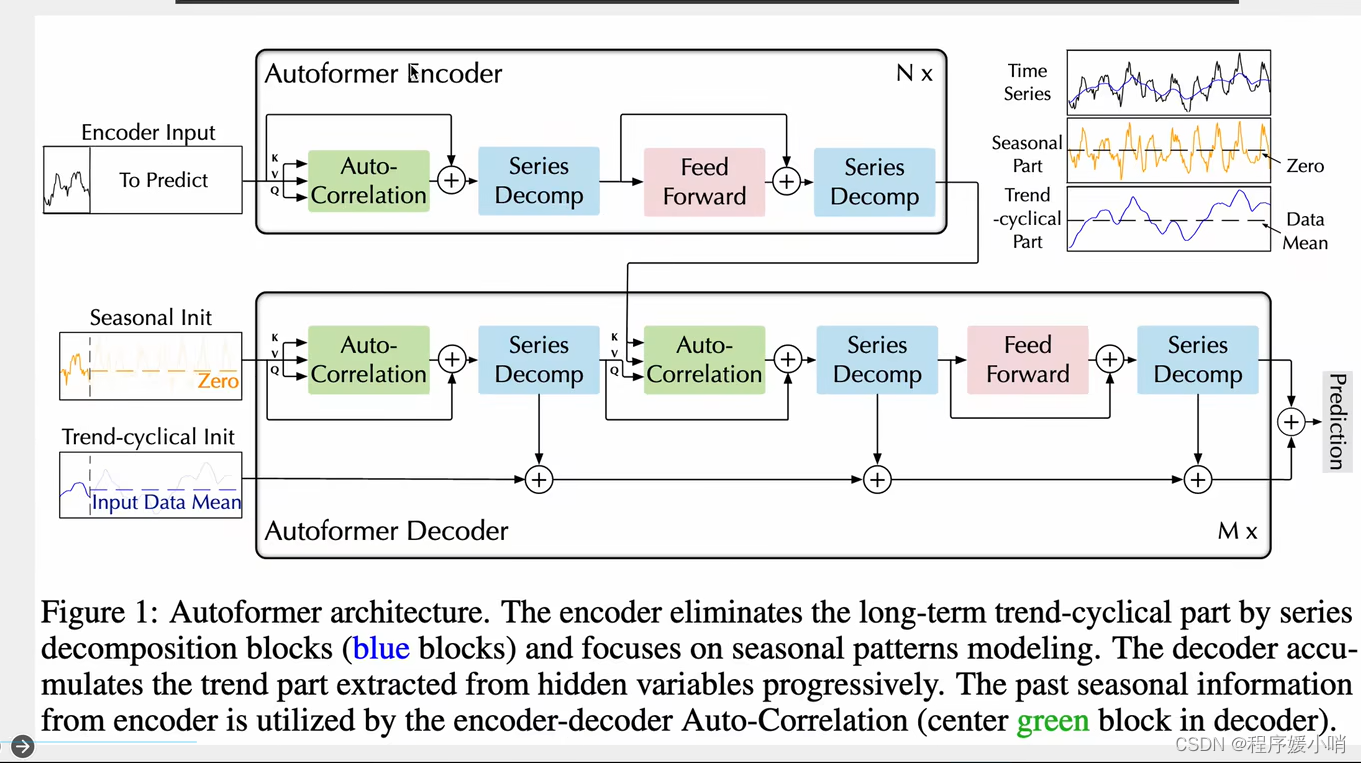
一个transformer encoder结构，一个transformer decoder结构。

跟transformer的区别体现在两个创新点：
①Series Decomp 序列的分解：时间序列做季节性分解（周期性），和趋势分解
②Autoformer自注意力机制：他认为时间序列的自注意力机制不能简简单单的根据数值来判断，应该根据其他东西，应该根据趋势来判断

原始输入 =
季节性输入（初始化zero）
+
趋势输入（初始化均值）

通过encoder输入input 做一个拆分得到
ens: encoder senson
ent: encoder trend
通过对ens和0拼接得到
des: decoder senson
通过对ens和mean均值做拼接得到
det: decoder trend

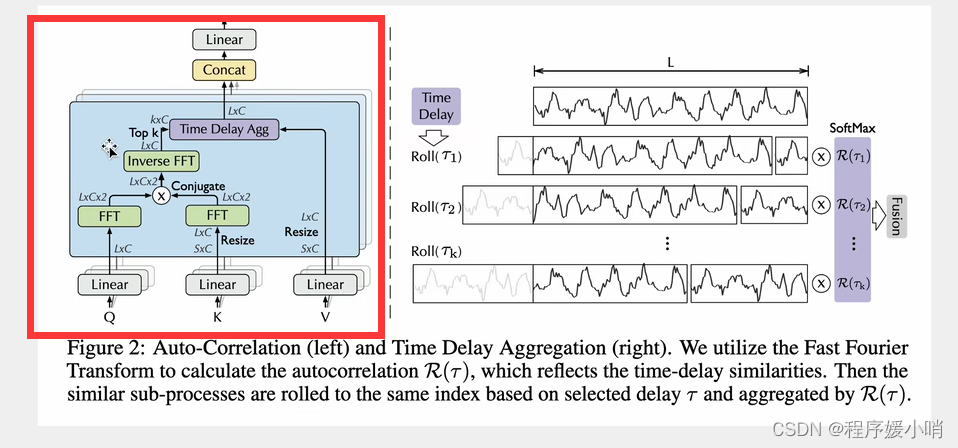
Auto-Correlation

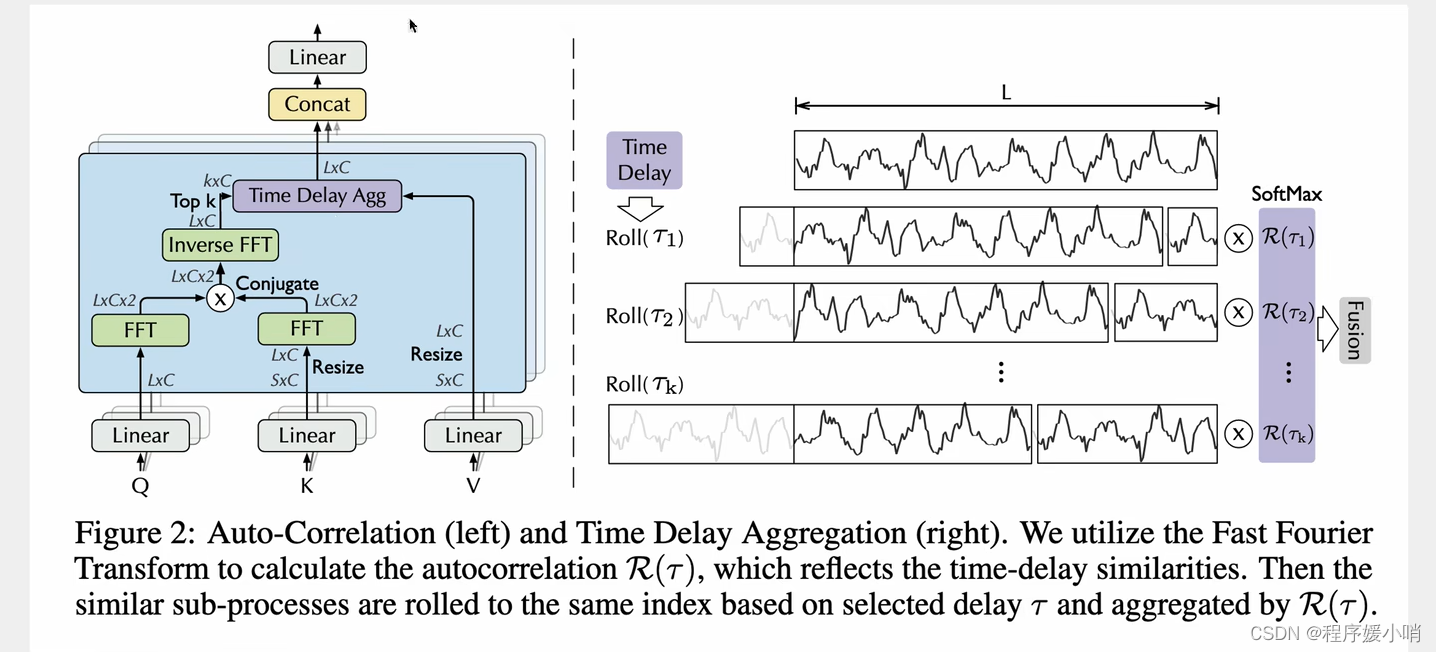
采用了多重注意力机制，把原来通道拆分成3个然后拼起来，拿到QKV
K表示从S扩张到L
Q是卷积
QK丢过来做一个傅里叶变换（相当于把Q,K给拆了），傅里叶变换的结果再相乘在做一个逆傅里叶变换得到原始的（然后再把QK乘完的结果运算回去得到原来的）

再把右边拼接起来得到多头带注意力的值。（注意力计算之后的数据）

怎们算的：

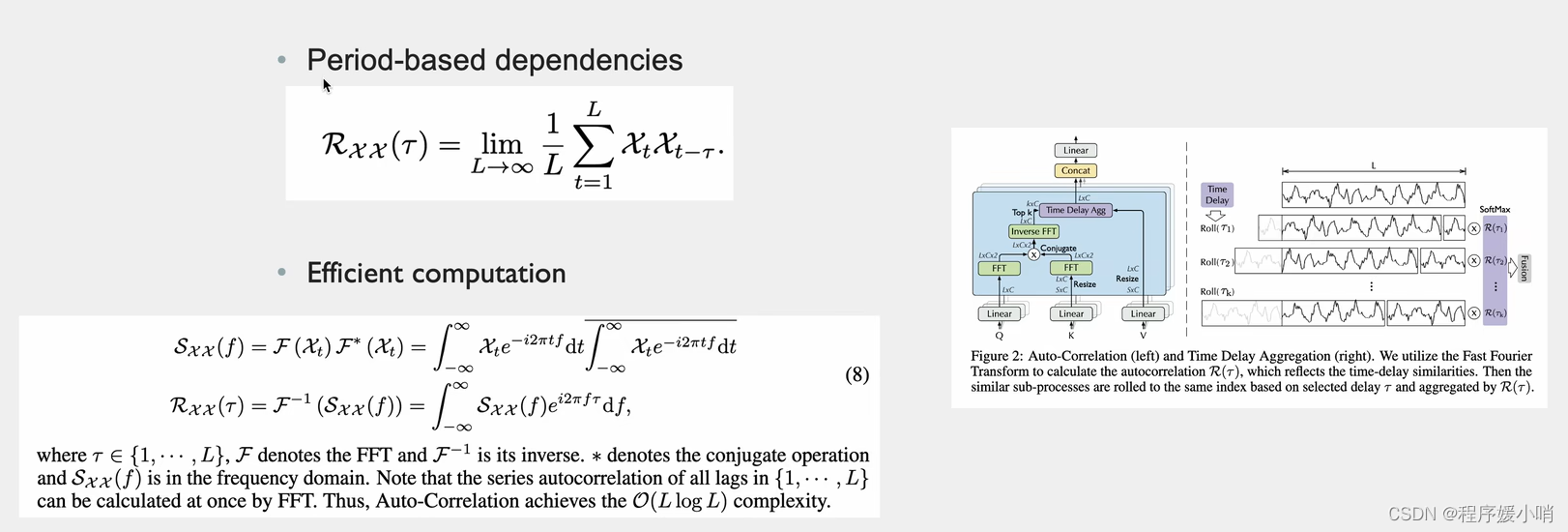
根据随机过程里面有一个很重要的结论：Period-based dependencies

和相关性 Xt是长度为L通道数为1的分量(随机过程里面的变量)把这个和他自己τ时刻之前的变量做一个相关性检测（乘法）
把L个点都加起来取一个平均值，得到以τ为时间窗口的相关性系数。

如右图τ1一个高峰的长度，把它放到后面去，两两点比较，每两个点差值是τ1
τ2同理，把τ2长度的点拼接到后面去，每两点比较，每两个点差值是τ2

把他们两个相乘就是原时刻数据和他τ时刻之前的数据的相关性

上面是定义，真正做起来是这么做的
先把QK做傅里叶变换（把随机过程中的每一个变量都要拆分出来，拆分的结果值是2，说明只拆分了2个），其中K的傅里叶变换的结果需要取一个共轭（实数相同，虚数相反），为了两个数相乘的时候把虚数部分抵消掉。为什么要相乘就是该时刻和他自己τ时刻之前的变量做一个相关性乘法

相乘后乘完后的结果做一个逆傅里叶变换，把分解后的函数给他合起来，合成原函数，L*C
τ从1到L（遍历错位的L种情况），每种情况有好有坏这就是个标量的集合了

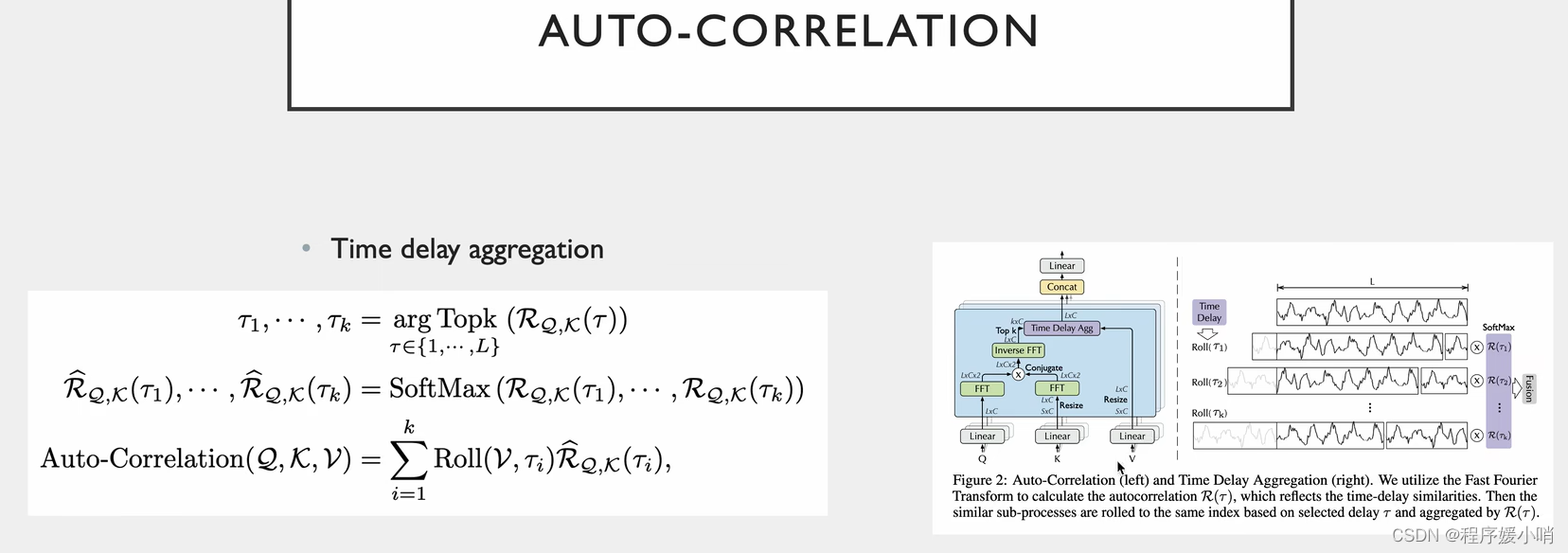
有L*C种情况，那我们就取k个最大的（每种移动方法有好有坏，肯定取最好的）得到图右边那部分

得到最好的k个以后再做一个softmax，保证他们的和是1

softmax以后再乘以V(第一行是原始值，后面是平移之后的值，平移的v就是不同的τ，不同的τ乘以τ的相关系数)

最后在做一个融合就是L*C个，这个就是带注意力值的一个矩阵，原来的输入就变成了带注意力值的输入

最后经过多头的话，再做一个拼接

多头就是把原来的通道分为3份，原来有3c个通道，除以3后每个头就有c个通道。纯纯是为了加速。同时也能提升注意力的效果。

下图是自动相关注意力机制和常见注意力机制进行对比

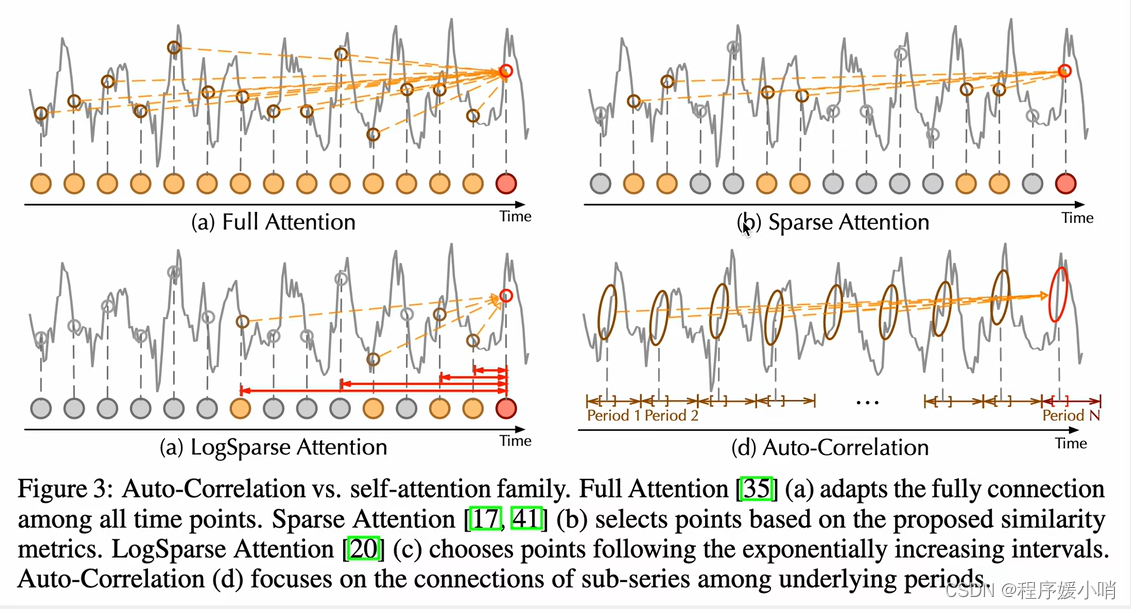
左上某一个时刻点和所有时刻相关性的乘法，基于数值，效果会非常差

右上（分散型注意力）不和所有点做一个注意力乘法，只是分散，分散的依据有很多（Informer用的概率稀疏的注意力乘法，根据分布的相似度，如果两个分布越相似，相似度越高，取前几个最相似的做注意力，图例种的几个点就是函数上比较相似）

左下（Log相似度 by LogTransformer）他的取样不是根据相似度，是根据固定的指数增长的一个间隔，完全根据间隔来

右下（根据周期来的）找不同的τ每一个点都跟τ之前的点比较，把这n个点连起来，就是n个点和n个点前时刻的点做一个相关性计算。

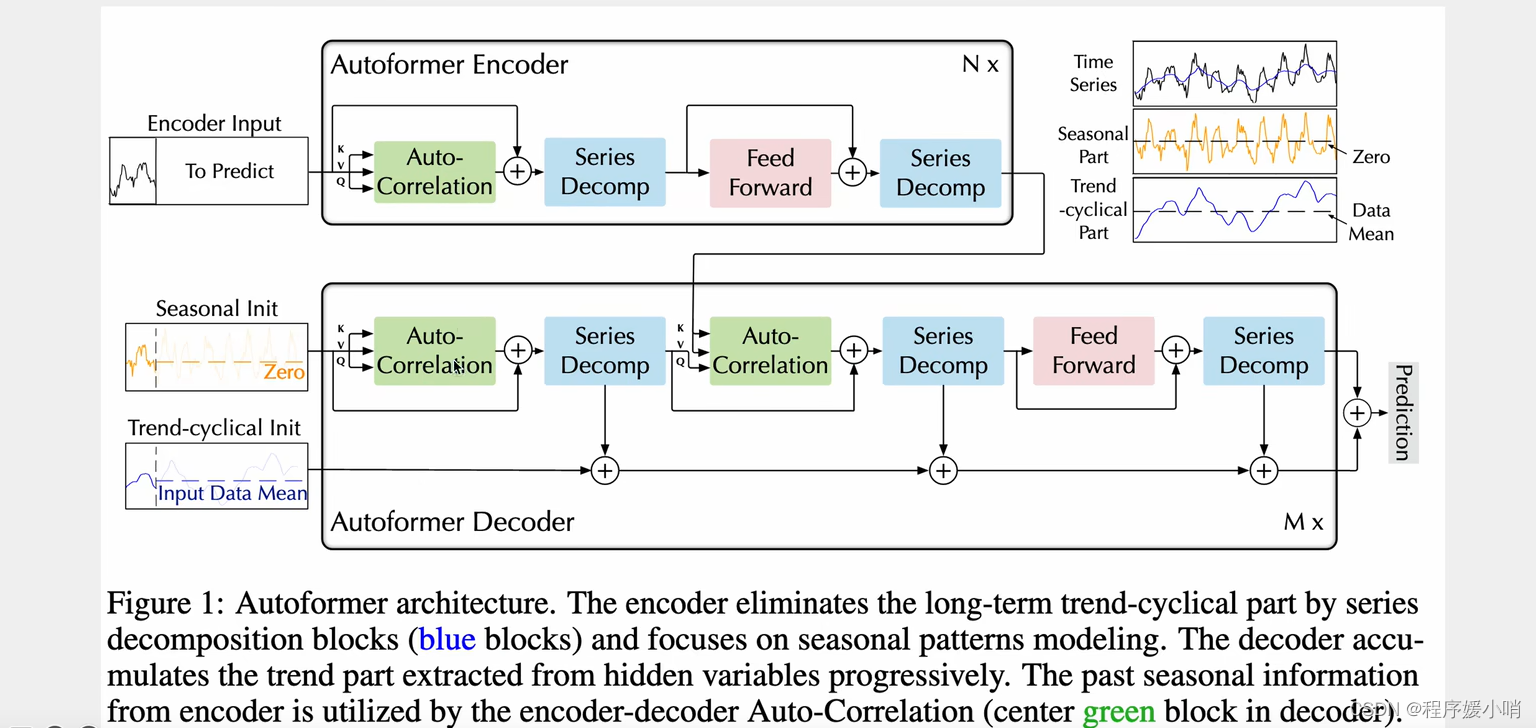
值得提的就是周期性的趋势不参与自注意力计算，只是最后做一个加法，趋势分解之后，它分解出来的这个部分又和原来的做一个加法。每次一分解就和原来的做加法，最后又加回去了，趋势性和季节性的都加回去了

这个模型侧重于季节性的提取

Dataset

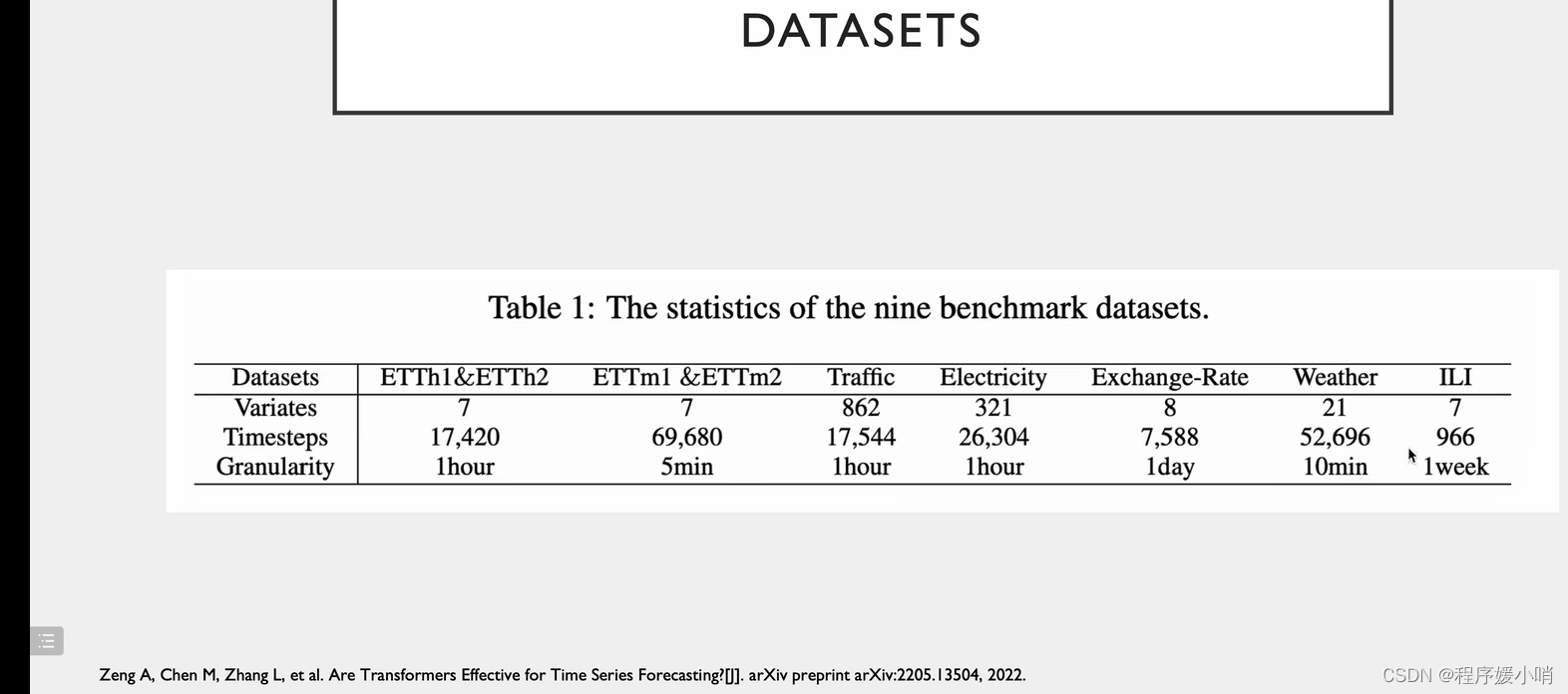
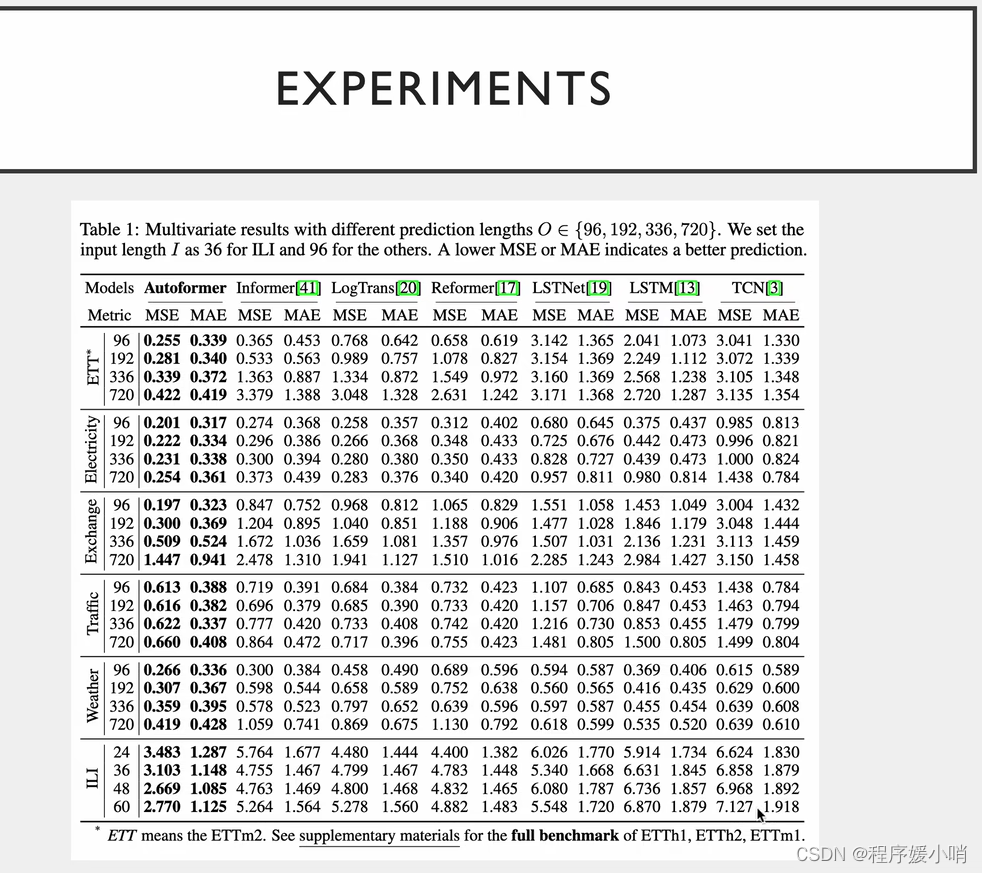
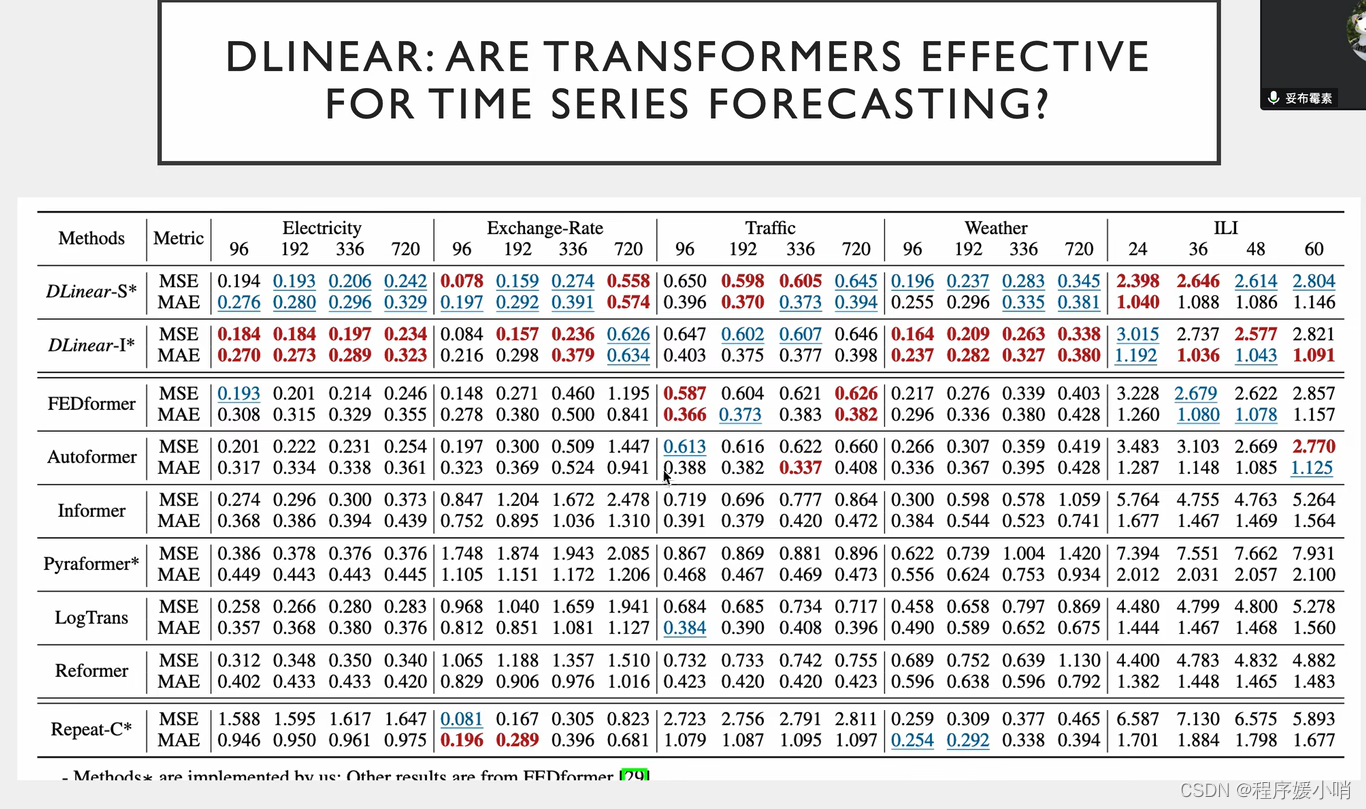
相关实验，把注意力机制换掉

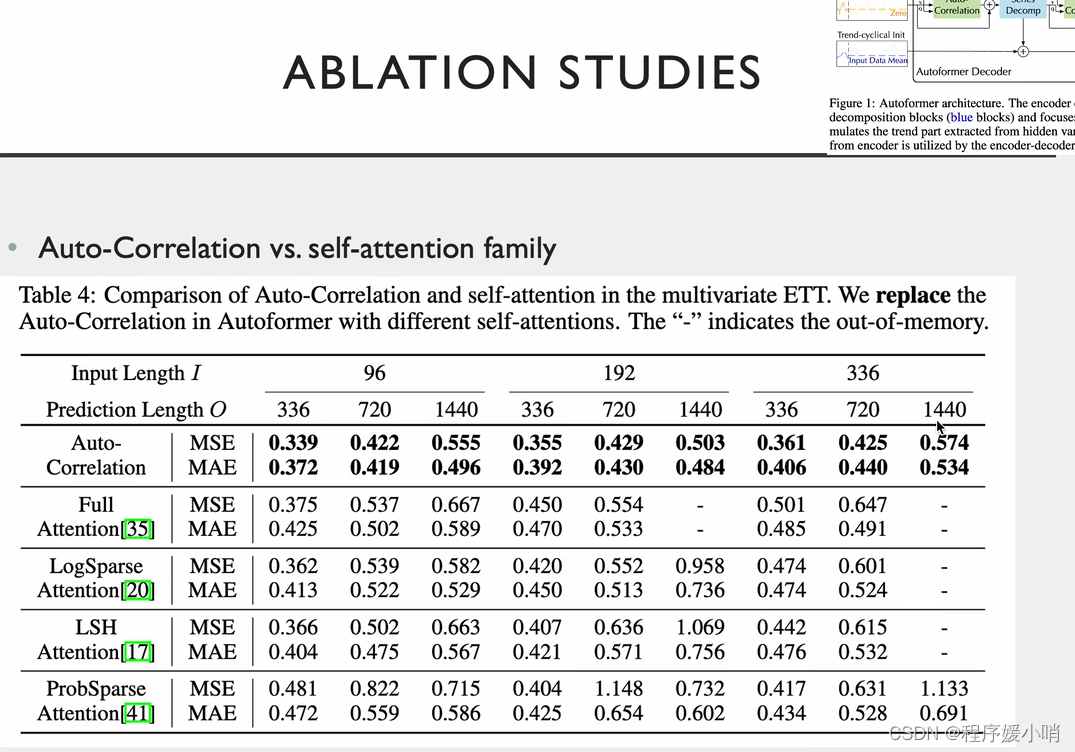
在原来的里面加了分解模型的效果

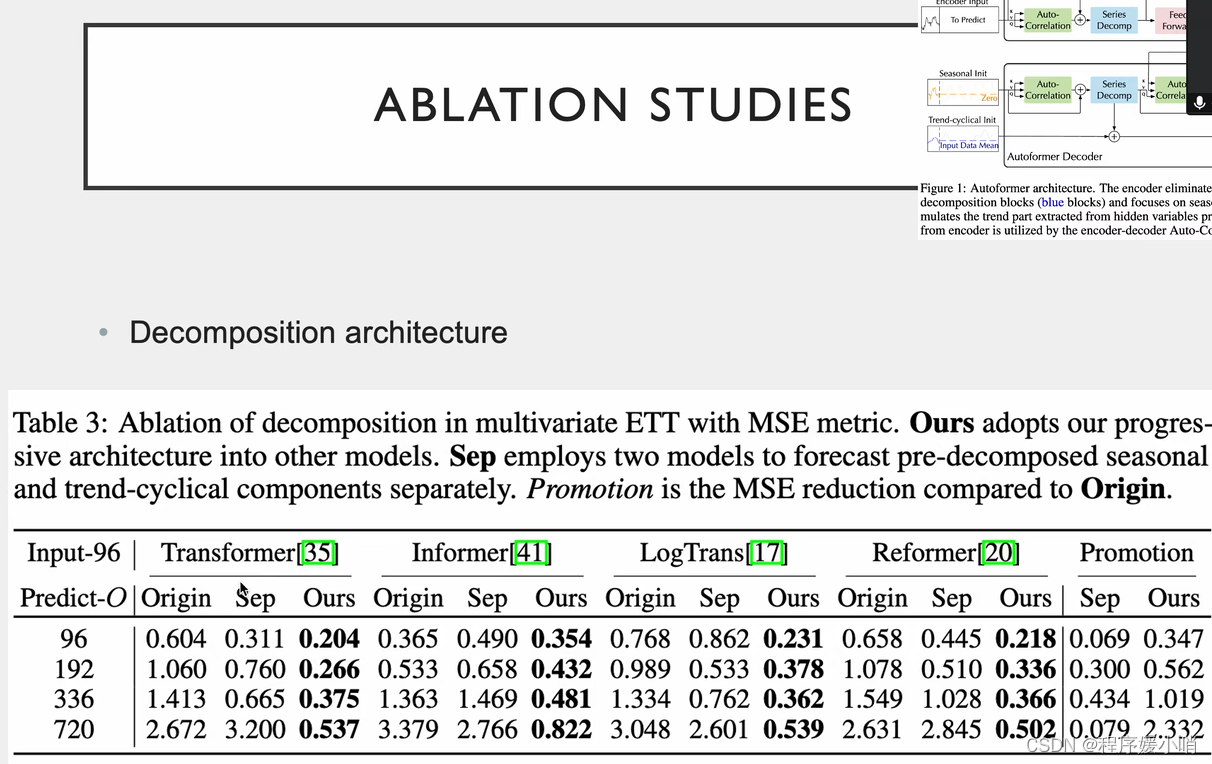
两个创新点都能用
注意力 QKV做线性变换的， LogTrans提出把线性层换成卷积层会有效果的提升

序列的分解方法

数据集都是带时间周期的，tranffic有两个，早高峰晚高峰，周一
Dlinear效果最好但是不能发文章

基于Transformer的模型采用各种注意力机制来发现长期依赖关系，但是有两个两个挑战:
未来的时间模式复杂,难以找到可靠的时间依赖。
为了应对长序列时有效率，Transformer采用稀疏的point-wise自注意力，导致信息利用效率低。
本文提出Autoformer将序列分解这一预处理，更新为一个内部块，实现渐进式的预测Decomposition Architecture 。
在随机过程理论基础上，设计基于序列周期性的Auto-Correlation机制。不再是point-wise而是series-wise。在子序列层次上进行相关性发现和表示聚合。

在这段话中，"point-wise"和"series-wise"是指自注意力机制中所涉及的不同数据点的关系表示方式。

在传统的Transformer中，自注意力机制是基于点之间的相对位置来计算注意力分数的，因此称为point-wise。具体地说，每个词嵌入向量都会与序列中的所有其他向量进行比较，并计算它们之间的相似度得分，然后使用这些得分来加权平均所有向量以获得上下文表示。

相比之下，Autoformer使用的是series-wise的注意力机制。这意味着它考虑的是序列中子序列的关系，而不是单个词之间的关系。这种注意力机制可以更好地捕捉到序列中长距离的依赖关系，因为它不受点与点之间距离的影响，而是考虑序列上的周期性结构。

具体来说，Autoformer采用了一种基于序列周期性的自相关机制，用于在子序列级别上计算注意力分数，以捕捉序列中的长期依赖关系。这种机制利用了序列中的重复模式，并将它们表示为周期函数，

在Transformer中，点积注意力（也称为point-wise自注意力）是一种机制，用于计算输入序列中每个位置与其他位置之间的相对重要性，以便进行下一步的处理。Point-wise自注意力通过对所有输入位置进行显式计算来实现这一点，这可能会导致在处理长序列时出现效率问题，因为它需要大量的计算资源和内存空间。

相比之下，Autoformer中采用的是序列分解（Decomposition Architecture）的预处理方式。它将长序列分解为多个子序列，每个子序列都可以独立地进行处理，以减少计算和存储的负担。这种方法实现了渐进式的预测，从而提高了效率。

在Autoformer中，还采用了一个基于序列周期性的自相关（Auto-Correlation）机制，以替代点积注意力。自相关是一种衡量序列中不同部分之间相关性的方法，可以通过计算序列在不同时间点上的相似度来实现。这种机制在子序列层次上发现和表示相关性，从而实现了series-wise处理。与point-wise自注意力相比，series-wise处理可以更有效地捕获序列中的长期依赖关系，并提高模型的表现力。

在Transformer模型中，point-wise通常指的是通过一个全连接层（也称为线性层）来对每个位置的向量进行非线性转换。这个操作也被称为多层感知机（MLP）层。

具体来说，在Transformer的自注意力层中，每个输入向量会分别经过三个线性变换，即查询（query）、键（key）和值（value）变换。然后，通过计算查询向量和键向量的点积，再经过softmax函数的归一化，最后将值向量加权求和，就得到了自注意力层的输出。其中，每个向量都可以经过一个点-wise的前馈神经网络，也就是一个全连接层，来增强其表示能力。

这个全连接层的作用是将每个向量的每个维度作为输入，通过一个非线性的函数映射到一个新的向量空间，以获得更丰富的特征表达。这种操作是点-wise的，因为它是对每个向量的每个维度进行独立的转换，而不是像卷积神经网络中的卷积操作一样，对整个向量进行变换。

在Transformer模型中，Multi-Head Attention和Self-Attention（自注意力机制）是两个不同的概念，但它们在Transformer中密切相关，并且通常一起使用。

Self-Attention是一种计算输入序列中每个位置与其他位置之间的关联程度的机制。在Transformer中，每个输入向量将同时经过三个线性变换，分别变成查询（query）、键（key）和值（value）向量，然后计算查询向量和键向量的点积，再经过softmax函数的归一化，最后将值向量加权求和，得到自注意力层的输出。这个过程是针对输入序列内部不同位置之间的关系进行计算的。

Multi-Head Attention是将Self-Attention机制复制多份，每份分别计算不同的query、key、value向量，并在输出后进行concatenation（拼接）操作。这样做的好处是能够让模型在不同的“头”（即不同的注意力机制）上学习不同的特征，提高模型的表示能力。Multi-Head Attention通常包括多个并行的Self-Attention计算，通过在不同的query、key、value向量上进行投影，从而使得模型能够同时关注输入序列的不同方面。

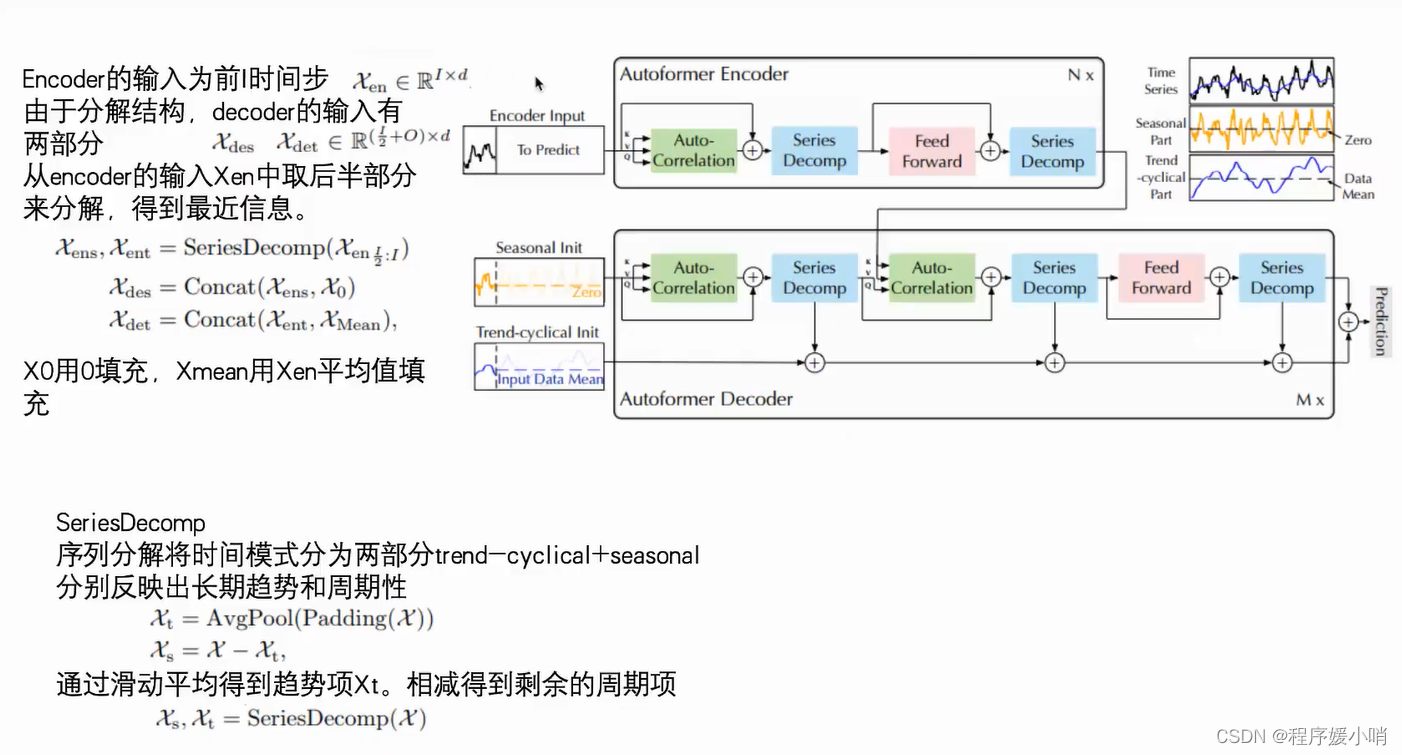
序列分解快

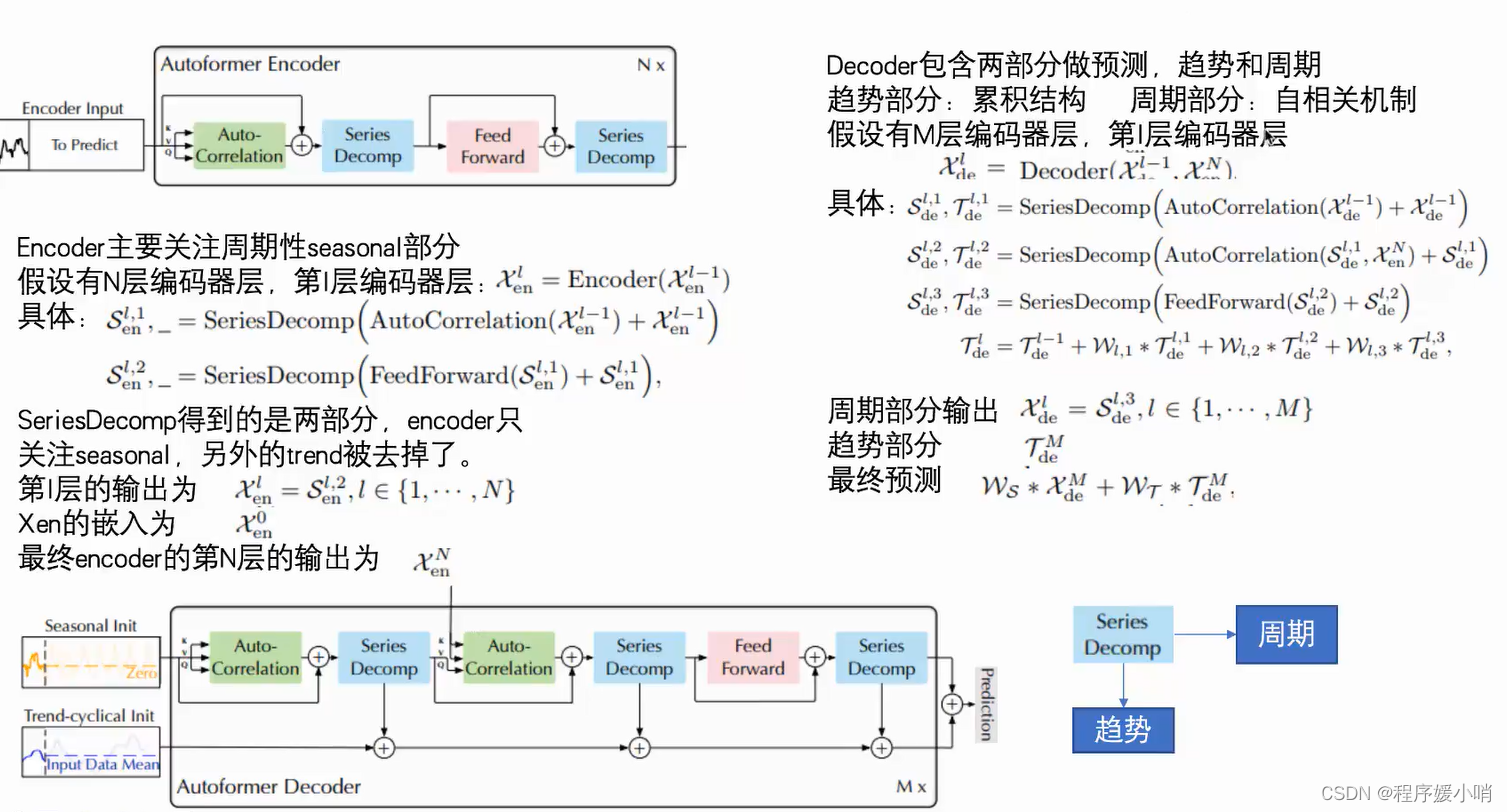
Encoder部分的主要目的是对复杂的季节项进行建模。通过多层的Series Decomposition Block，不断从原始序列中提取季节项。这个季节项会作为指导Decoder在预测未来时季节项的信息。

该方程由两条线组成，每条线描述了 Autoformer 架构中的不同步骤。第一行描述了 SeriesDecomp 步骤，该步骤将输入的时间序列数据分解为子序列。输入数据表示为 Xen (l-1)，其中 l 是层号，-1 表示前一层。自动关联机制应用于输入数据，该数据在子系列级别进行依赖关系发现和表示聚合。将自动关联机制的输出添加到输入数据中，然后将生成的和通过 SeriesDecomp 函数传递以获得输出的子系列数据。此输出表示为 Sen (l,1)，其中 1 表示第一个子系列。

第二行描述了 FeedForward 步骤，该步骤将前馈神经网络应用于从第一行获得的输出子系列数据。将前馈网络的输出添加到输入子系列数据中，然后通过SeriesDecomp函数传递生成的总和以获得最终的输出子系列数据。此输出表示为 Sen (l,2)，其中 2 表示第二个子系列。

SeriesDecomp 函数是一种新颖的设计，它打破了序列分解的预处理惯例，将其更新为深度模型的基本内部模块。这种设计使 Autoformer 具有复杂时间序列的渐进分解能力。自相关机制受随机过程理论的启发，基于序列周期。它在效率和准确性方面都优于自我注意力。

该方程显示了模型每层 (l) 的分解过程。第 l-1 层的输入时间序列表示为 Xde (l-1)。将自相关机制应用于 Xde (l-1) 以获得分解后的子序列，然后将其添加到 Xde (l-1) 中。然后通过 seriesDecomp 函数传递这个总和以获得两个输出：Sde (l,1) 和 Tde (l,1)。Sde (l,1) 是分解后的子系列，而 Tde (l,1) 是捕捉剩余模式和依赖关系的残差序列。

对于 Sde (l,1) 和 Xen (N)（最后一层的输入时间序列）重复相同的过程，生成 Sde (l,2) 和 Tde (l,2)。最后，通过 FeedForward 函数传递 Sde (l,2) 以获得 Sde (l,3) 和 Tde (l,3)。然后使用权重（Wl1、Wl,2 和 Wl,3）对 SeriesDecomp 函数（Tde (l,1)、Tde (l,2) 和 Tde (l,3)）的输出进行合并，得出最终的分解序列 Tde (l)。

总体而言，此过程允许Autoformer模型逐步将输入时间序列分解为较小的子序列，从而捕获复杂的时间模式和依赖关系。自动关联机制是根据序列的周期性设计的，这有助于在子序列级别上有效地发现和表示依赖关系。这种方法在效率和准确性方面都优于基于 Transformer 的模型中使用的传统自我注意力机制。Autoformer 模型在长期预测方面实现了最先进的准确性，与涵盖能源、交通、经济、天气和疾病等实际应用的六个基准相比，相对提高了 38%。该模型的代码可在提供的存储库中找到。