🎊专栏【数据结构】
🍔喜欢的诗句:更喜岷山千里雪 三军过后尽开颜。
🎆音乐分享【勋章】
大一同学小吉,欢迎并且感谢大家指出我的问题🥰
目录
⭐栈的分类
✨顺序栈
🎈优点:
🎈缺点:
✨链栈
🎈优点:
🎈缺点:
⭐基本概念
✨栈:
✨栈顶:
✨栈顶:
✨图片理解
⭐基本操作
⭐顺序栈 的详细操作
🎊定义
🎊初始化
🎈算法步骤
🎈算法描述
🎊入栈
🎈算法步骤
🎈算法描述
🎊出栈
🎈算法步骤
🎈算法描述
🎊取栈顶元素
🎈算法步骤
🎈算法描述
🎊遍历栈
🎈算法步骤
🎈算法描述
🎊置空栈
🎈算法步骤
🎈 算法描述
🍔完整代码
⭐链栈 的详细操作
🎊定义
🎊初始化
🎈算法步骤
🎈算法描述
🎊入栈
🎈算法步骤
🎈算法描述
🎊出栈
🎈算法步骤
🎈算法描述
🎊取出栈顶元素
🎈算法步骤
🎈算法描述
🎊遍历
🎈算法步骤
🎈算法描述
🍔完整代码
⭐栈的分类
✨顺序栈
🎈优点:
-
插入和删除操作方便高效:顺序栈只允许在表尾进行插入和删除操作,所以插入和删除非常方便。在栈顶进行插入和删除操作时,不需要移动其他元素,只需修改栈顶指针即可,因此操作非常高效。
-
存储结构简单明了:顺序栈的存储结构非常简单明了,只需要一个一维数组即可实现。栈顶指针指向的就是当前栈顶元素的位置,因此非常容易理解和实现。
-
方便实现逆序操作:由于栈遵守后进先出的原则,所以可以方便地实现逆序操作。比如说,可以将一个字符串中的字符倒序输出,只需要将字符依次入栈,再依次出栈即可。
🎈缺点:
-
存储空间受限:顺序栈的存储空间是固定的,所以当栈满时,无法再插入新的元素。如果需要存储更多的元素,就需要重新分配存储空间或者使用其他的数据结构。
-
不支持随机访问:由于栈的特性,只能从栈顶进行插入和删除操作,无法在任意位置插入或删除元素,也无法随机访问栈中的元素。如果需要支持随机访问,就需要使用其他的数据结构。
-
容易产生溢出:由于栈的特性,一旦栈满并且继续插入元素,就会发生栈溢出。而且由于栈的深度通常比较有限,所以这种情况很容易出现。
-
非线程安全:线性栈在多线程环境下容易出现问题,如果多个线程同时进行栈的操作,可能会导致栈的状态不一致,需要进行同步处理。
✨链栈
🎈优点:
-
存储空间动态可调整:链栈的存储空间是动态可调整的,可以随时根据需要进行扩容或缩容。这使得链栈能够更好地应对数据的变化。
-
不受固定大小限制:与线性栈不同,链栈的大小不受固定大小的限制,可以处理任意长度的数据。这使得链栈非常适合于处理变长的数据。
-
不易产生溢出:由于链栈的存储空间是动态可调整的,所以不会像线性栈一样容易产生溢出问题。
-
支持随机访问:与线性栈不同,链栈支持在任意位置插入或删除元素,也支持随机访问栈中的元素。因此,链栈比线性栈更加灵活。
🎈缺点:
-
需要额外的存储空间:与线性栈不同,链栈需要额外的指针来表示元素之间的关系,因此需要更多的存储空间。
-
操作效率低:相对于线性栈来说,链栈的操作效率比较低,因为在进行插入和删除操作时需要进行指针的重新指向操作。同时由于内存分配和释放的开销,链栈的性能也可能受到一定的影响。
-
不支持随机访问:尽管链栈支持在任意位置插入或删除元素,并且支持访问栈中的元素,但是由于链表的特性,链栈不支持随机访问,因此在需要频繁进行随机访问的场景下,链栈并不适用。
-
存在指针空间浪费和指针跳转问题:链栈的每个节点都包含一个指针,这会导致存储空间的浪费。同时,由于链表中相邻节点之间不一定连续存储,因此在访问相邻节点时需要通过指针进行跳转,这也会影响操作的效率。
⭐基本概念
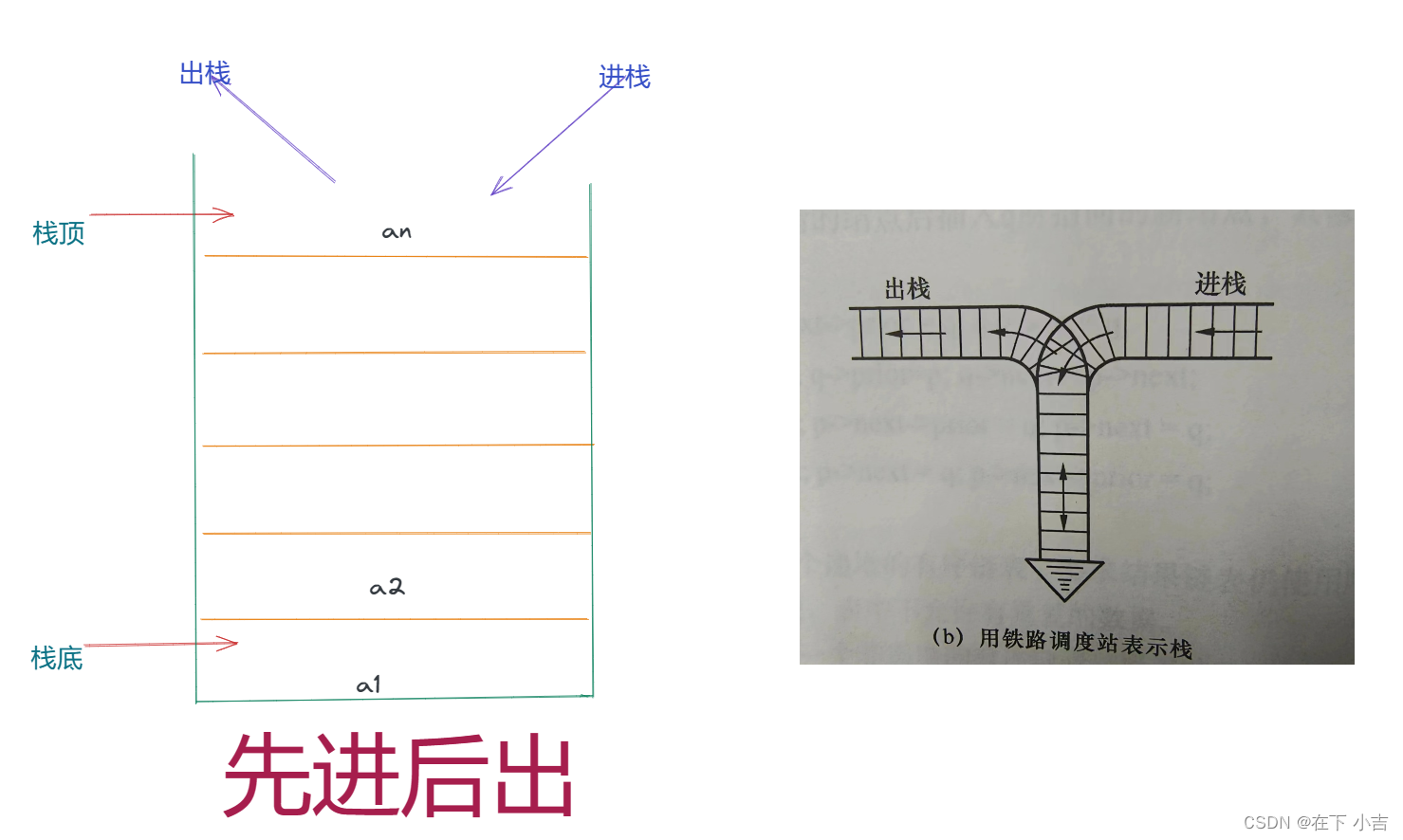
✨栈:
只能在表尾进行插入或删除操作的线性表,
✨栈顶:
表尾端
✨栈顶:
表头端
✨图片理解
⭐基本操作
✨定义
✨初始化
✨入栈
✨出栈
✨取栈顶元素
✨遍历
✨置空
⭐顺序栈 的详细操作
🎊定义
顺序栈是指利用顺序存储结构实现的栈,即利用一组地址连续的存储单元依次存放自栈底到栈顶的数据元素,同时附设指针top指示栈顶元素在顺序栈中的位置。鉴于C++中数组的下标约定从0开始,则当以C++作描述语言时,如此设定会带来很大不便,因此另设指针base指示栈底元素在顺序栈中的位置。当top和base的值相等时,表示空栈。顺序栈的定义如下:
typedef int SElemType;
#define max 100
typedef struct{
SElemType *base;
SElemType *top;
int stacksize;
}SqStack; 🎊初始化
🎈算法步骤
1.为顺序栈动态分配一个最大容量为maxsize的数组空间,使base指向这段空间的基地址,即栈底
2.栈顶指针top初始化为base,表示栈为空
(S.top=S.base,不是S.base=S.top,顺序别错了)
3.stacksize置于栈的最大容量maxsize
🎈算法描述
int InitStack(SqStack &S)
{
S.base=new int[100];
if(!S.base) return overflow;
S.top=S.base;
S.stacksize=max;
return 1;
}🎊入栈
base为栈底指针,初始化完成后,栈底指针base始终指向栈底的位置,若base的值NULL,则表明栈结构不存在。top为栈顶指针,其初值指向栈底。每当插入新的栈顶元素时,指针top增1;删除栈顶元素时,指针top减1、因此,栈空时,top和base的值相等,都指向栈底;栈非空时,top始终指向栈顶元素的上一个位置

我们定义一个top变量来指示栈顶元素在数组中的位置,top就如同中学物理学过的游标卡尺的游标,如下图,它可以来回移动,意味着栈顶的top可以变大变小,但无论如何游标不能超出尺的长度。同理,若存储栈的长度为StackSize,则栈顶位置top必须小于StackSize。当栈存在一个元素时,top等于0,因此通常把空栈的判定条件定为top等于-1。

🎈算法步骤
1.判断栈是否满,如果满,返回-1
2.将新元素压入栈顶,栈顶指针+1
(先给栈顶元素赋值,然后指针再+1)
🎈算法描述
int Insert(SqStack &S,int e)
{
if(S.top-S.base==S.stacksize) return -1;
*S.top=e;
S.top++;
return 1;
}🎊出栈
出栈就是删除栈顶元素
🎈算法步骤
1.判断栈是否空,如果空,返回-1
2.栈顶指针-1,栈顶元素赋给e
(先指针-1,后赋值)
🎈算法描述
int Delete(SqStack &S,int &e)
{
if(S.base==S.top) return -1;
else
{
S.top--;
e=*S.top;
}
return OK;
} 🎊取栈顶元素
栈非空时,这个操作返回当前栈顶元素的值,栈顶指针保持不变
🎈算法步骤
栈顶指针不变,返回栈顶元素的值
🎈算法描述
int PushOut(SqStack &S)
{
if(S.base!=S.top)
return *(S.top-1);//当前栈顶元素的值,栈顶指针保持不变
}🎊遍历栈
🎈算法步骤
1.创建一个新指针
2.从栈顶遍历到栈底
(注意:p指针要先-1再输出值,因为top指针在栈顶元素的上一个位置)
🎈算法描述
void Search(SqStack &S)
{
int* p;
p = S.top;
while (p != S.base)
{
p--;
cout << *p << endl;
}
}🎊置空栈
🎈算法步骤
top指针=base指针时,为空
🎈 算法描述
int kong(SqStack &S)
{
S.top=S.base;
return 1;
}🍔完整代码
#include<iostream>
using namespace std;
typedef int SElemType;
#define max 100
#define OK 1
#define overflow -1
typedef struct{
SElemType *base;
SElemType *top;
int stacksize;
}SqStack;
//1
int InitStack(SqStack &S)
{
S.base=new int[100];
if(!S.base) return overflow;
S.top=S.base;
S.stacksize=max;
return 1;
}
//2
int Insert(SqStack &S,int e)
{
if(S.top-S.base==S.stacksize) return -1;
*S.top=e;
S.top++;
return 1;
}
//3
int Delete(SqStack &S,int &e)
{
if(S.base==S.top) return -1;
else
{
S.top--;
e=*S.top;
}
return OK;
}
//4
int PushOut(SqStack &S)
{
if(S.base!=S.top) return *(S.top-1);
}
//5
void Search(SqStack &S)
{
int* p;
p = S.top;
while (p != S.base)
{
p--;
cout << *p << endl;
}
}
int kong(SqStack &S)
{
S.top=S.base;
return 1;
}
int main()
{
SqStack S;
int n,num,s,cnt,e;
cout<<"1 初始化"<<endl;
cout<<"2 插入元素,从而建立栈"<<endl;
cout<<"3 删除栈顶元素"<<endl;
cout<<"4 取出栈顶元素"<<endl;
cout<<"5 遍历栈"<<endl;
cout<<"6 置空栈"<<endl;
cout<<"0 结束"<<endl;
for(;;)
{
cin>>n;
switch(n)
{
case 1:
if(InitStack(S)) cout<<"建栈成功"<<endl;
else cout<<"建栈失败"<<endl;
break;
case 2:
cout<<"请输入需要插入元素的个数"<<endl;
cin>>num;
for(int i=0;i<num;i++)
{
int e;
cin>>e;
if(Insert(S,e)) cout<<"插入成功"<<endl;
else cout<<"插入失败"<<endl;
}
break;
case 3:
int ee;
if(Delete(S,ee))
{
cout<<"栈顶元素删除成功"<<ee<<endl;//注意,输出的是ee,而不是Delete(S,ee)
num--;
}
else cout<<"栈顶元素删除失败"<<endl;
break;
case 4:
cout<<"取出栈顶元素"<<endl;
cout<<PushOut(S)<<endl;
break;
case 5:
cout<<"遍历栈"<<endl;
Search(S);
break;
case 6:
if(kong(S)) cout<<"置空成功"<<endl;
break;
case 0:
return 0;
break;
}
}
}⭐链栈 的详细操作
🎊定义
链栈是采用链式存储结构实现的栈,通常链栈用单链表表示,链栈的结构与单链表的结构相同
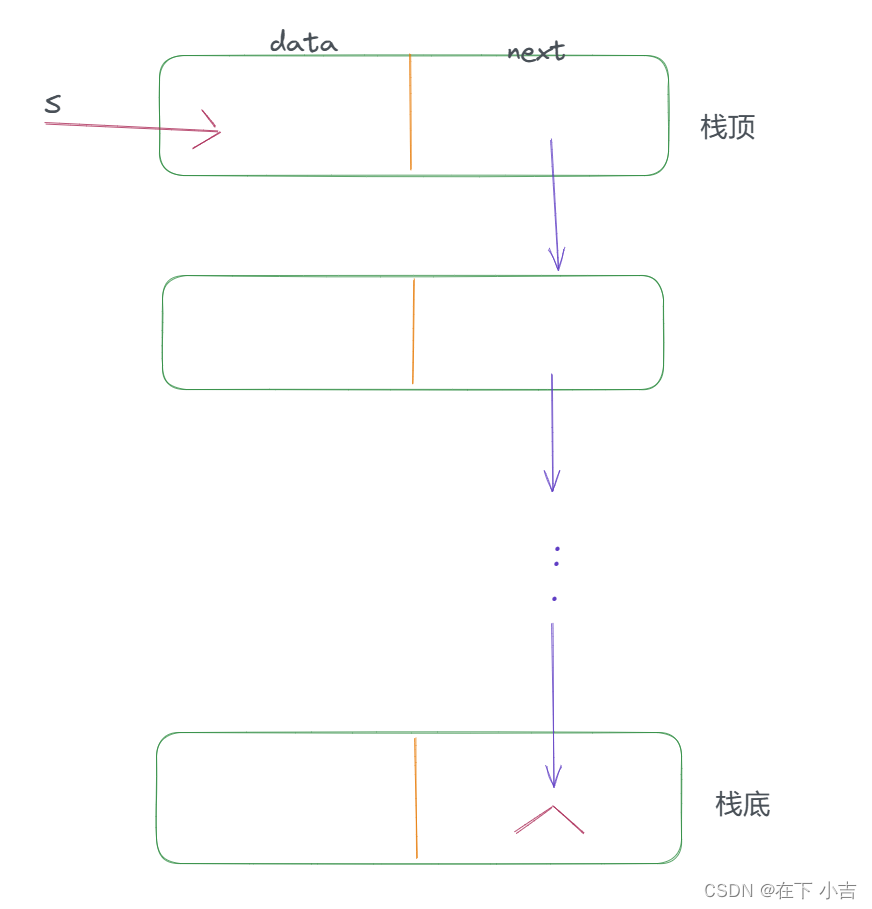
typedef struct StackNode {
int data;
struct StackNode* next;
} StackNode, * LinkStack;由于对栈的主要操作是在栈顶插入和删除元素,显然以链表的头部作为栈顶是最方便的,所以没必要像单链表那样为了操作方便而附加一个头结点
🎊初始化
🎈算法步骤
构造一个空栈,因为没有必要设置头结点,使用直接把栈顶指针置空即可
🎈算法描述
int InitStack(LinkStack& S) {
S = NULL;
return OK;
}🎊入栈
与顺序栈的入栈不同,链栈不用判断栈是否空,只为入栈元素动态分配一个结点空间即可
🎈算法步骤
1.为入栈元素e分配空间,用指针p指向这个空间
2.将新结点的数据域设置为e
3.将新结点插入栈顶
4.修改栈顶指针为p
🎈算法描述
int Push(LinkStack& S, int e) {//在栈顶插入元素e
LinkStack p;
p = new StackNode; //生成新结点
p->data = e;
p->next = S; //将新结点插入 栈顶
S = p; //修改栈顶指针为p
return OK;
}🎊出栈
链栈出栈要判断是否为空,而且要释放出栈元素的栈顶空间
🎈算法步骤
1.判断栈是否为空,如果为空,返回ERROE
2.将栈顶元素赋给e
3.临时保存栈顶元素的空间,方便释放
4.修改栈顶指针,指向新的栈顶元素
5.释放原栈顶元素的空间
🎈算法描述
int Pop(LinkStack& S, int& e) {//删除S的栈顶元素,用e返回其值
LinkStack p;
if (S == NULL)
return ERROR;
e = S->data; //将栈顶元素赋给e
p = S; //用p临时保存栈顶元素空间,以备释放
S = S->next; //修改栈顶指针
delete p;
return OK;
}🎊取出栈顶元素
🎈算法步骤
栈非空时,返回栈顶元素,但是栈顶指针不变
🎈算法描述
char GetTop(LinkStack S) {//返回S的栈顶元素,不修改栈顶指针
if (S != NULL)
return S->data;
}
🎊遍历
🎈算法步骤
1.建立一个新结点p
2.p刚开始指向栈顶元素
3.p向下遍历,直到遍历到NULL截至
🎈算法描述
void StackTraverse(LinkStack S) {
LinkStack p; //使用指针p辅助访问栈里元素
p = S; //p初始从栈顶开始
cout << "从栈顶依次读出该栈中的元素值:"<<endl;
while (p != NULL)
{
cout << p->data<<endl;
p = p->next;
}
cout << endl;
}🍔完整代码
#include<iostream>
using namespace std;
#define OK 1
#define ERROR 0
#define OVERFLOW -2
typedef struct StackNode {
int data;
struct StackNode* next;
} StackNode, * LinkStack;
//1
int InitStack(LinkStack& S) {
S = NULL;
return OK;
}
//2
int Push(LinkStack& S, int e) {//在栈顶插入元素e
LinkStack p;
p = new StackNode; //生成新结点
p->data = e;
p->next = S; //将新结点插入 栈顶
S = p; //修改栈顶指针为p
return OK;
}
//3
int Pop(LinkStack& S, int& e) {//删除S的栈顶元素,用e返回其值
LinkStack p;
if (S == NULL)
return ERROR;
e = S->data; //将栈顶元素赋给e
p = S; //用p临时保存栈顶元素空间,以备释放
S = S->next; //修改栈顶指针
delete p;
return OK;
}
//4
char GetTop(LinkStack S) {//返回S的栈顶元素,不修改栈顶指针
if (S != NULL)
return S->data;
}
//5
void StackTraverse(LinkStack S) {
LinkStack p; //使用指针p辅助访问栈里元素
p = S; //p初始从栈顶开始
cout << "从栈顶依次读出该栈中的元素值:"<<endl;
while (p != NULL)
{
cout << p->data<<endl;
p = p->next;
}
cout << endl;
}
int main()
{
LinkStack s;
int e, t,n;
cout << "1.初始化"<<endl;
cout << "2.入栈"<<endl;
cout << "3.取栈顶元素"<<endl;
cout << "4.出栈"<<endl;
cout << "5.栈的遍历"<<endl;
cout << "0.退出"<<endl;
for(;;)
{
cin >> n;
switch (n)
{
case 1:
if (InitStack(s))
cout << "成功对栈进行初始化"<<endl;
else
cout << "初始化栈失败"<<endl;
break;
case 2:
cout << "输入要入栈的元素的个数"<<endl;
int nn;
cin>>nn;
for(int i=0;i<nn;i++)
{
cin>>e;
Push(s,e);
}
//cin >> e;
break;
case 3:
if (s != NULL)
cout << "栈顶元素为:" << GetTop(s) << endl;
else
cout << "栈中无元素,请重新选择" << endl;
break;
case 4:
cout << "弹出的栈顶元素为:" << Pop(s, t) << endl;
break;
case 5:
StackTraverse(s);
break;
case 0:
return 0;
}
}
return 0;
}
🥰如果大家有不明白的地方,或者文章有问题,欢迎大家在评论区讨论,指正🥰
Code over!