专栏导读

✍ 作者简介：i阿极，CSDN Python领域新星创作者，专注于分享python领域知识。

✍ 本文录入于《数据分析之术》，本专栏精选了经典的机器学习算法进行讲解，针对大学生、初级数据分析工程师精心打造，对机器学习算法知识点逐一击破，不断学习，提升自我。
✍ 订阅后，可以阅读《数据分析之术》中全部文章内容，详细介绍数学模型及原理，带领读者通过模型与算法描述实现一个个案例。
✍ 还可以订阅基础篇《数据分析之道》，其包含python基础语法、数据结构和文件操作，科学计算，实现文件内容操作，实现数据可视化等等。
✍ 其他专栏：《数据分析案例》 ，《机器学习案例》

1、梯度下降法原理

梯度下降法是一种常见的优化方法，常用于求解损失函数最小化的问题。在线性回归模型中，我们可以使用梯度下降法来求解使得模型损失函数最小的模型参数。

梯度下降法的基本思想是沿着当前位置梯度的反方向移动一小步，以期望能够到达函数的最小值点。
具体来说，我们假设$f(\theta )$表示模型的损失函数，其中$\theta$是模型的参数向量，损失函数的梯度为$\nabla f(\theta )$，那么梯度下降法的更新公式可以表示为：

$\theta =\theta -\eta \nabla f(\theta )$

其中$\eta$为学习率，表示更新步长的大小，需要手动指定。梯度下降法的过程中，我们从一个随机的初始参数向量${\theta }_0$开始，不断迭代，根据上式不断更新参数向量，直到达到最小化损失函数的要求，即：

$f({\theta }_{t+1})-f({\theta }_t)<ϵ$

其中$t$表示迭代次数，$ϵ$表示收敛的阈值，通常取一个很小的数值，比如$10^{-4}$。

在线性回归中，损失函数通常采用平方误差损失函数：

$L(\theta )=\frac{1}{2n}{\sum }_{i=1}^n(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$

其中$h_{\theta }(x^{(i)})$为模型对第$i$个样本的预测值，$y^{(i)}$为第$i$个样本的真实值。对该损失函数求梯度，我们得到：

$\nabla L(\theta )=\frac{1}{n}{\sum }_{i=1}^n(h_{\theta }(x^{(i)})-y^{(i)})x^{(i)}$

将该梯度代入梯度下降法的更新公式中，就可以求得线性回归模型的参数向量$\theta$。

2、梯度下降法原理代码实现

我们来用Python实现一个线性回归模型，使用梯度下降法来最小化成本函数。

首先，我们需要导入必要的库：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

然后，我们生成一个模拟数据集。这里我们使用numpy库的random.randn()函数生成100个样本数据，其中的真实关系是y=3x+2，同时为了模拟真实情况，我们在y上加上了一些噪声：

np.random.seed(0)
X = 2 * np.random.randn(100, 1)
y = 6 + 3 * X + np.random.randn(100, 1)

接下来，我们需要定义成本函数和梯度下降函数。成本函数采用均方误差（MSE）的形式：

def compute_cost(X, y, theta):
    m = len(y)
    predictions = X.dot(theta)
    cost = 1/(2*m) * np.sum(np.square(predictions-y))
    return cost

梯度下降函数则需要不断迭代，不断更新theta参数，直到成本函数最小化。迭代次数、学习率等超参数需要手动设置：

def gradient_descent(X, y, theta, learning_rate, iterations):
    m = len(y)
    cost_history = np.zeros(iterations)
    theta_history = np.zeros((iterations, 2))
    for i in range(iterations):
        predictions = X.dot(theta)
        error = predictions - y
        gradient = 1/m * X.T.dot(error)
        theta = theta - learning_rate * gradient
        theta_history[i,:] = theta.T
        cost_history[i] = compute_cost(X, y, theta)
    return theta, cost_history, theta_history

最后，我们需要将生成的数据集进行可视化，并且调用梯度下降函数来训练模型：

# 添加截距列
X_b = np.c_[np.ones((len(X), 1)), X]

# 定义初始theta值和超参数
theta = np.random.randn(2,1)
learning_rate = 0.1
iterations = 1000

# 训练模型
theta, cost_history, theta_history = gradient_descent(X_b, y, theta, learning_rate, iterations)

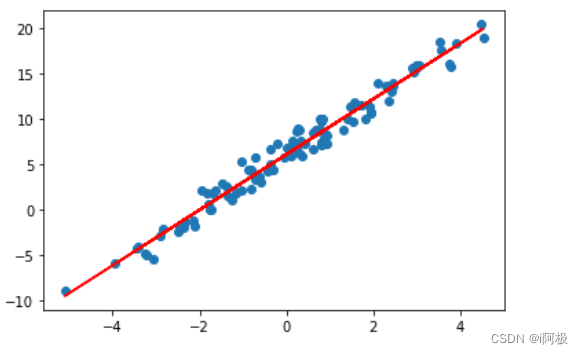
绘制模型拟合直线和数据点：

plt.scatter(X, y)
plt.plot(X, X_b.dot(theta), 'r')
plt.show()

绘制成本函数随迭代次数变化的曲线：

plt.plot(range(iterations), cost_history)
plt.xlabel('Iterations')
plt.ylabel('Cost')
plt.show()

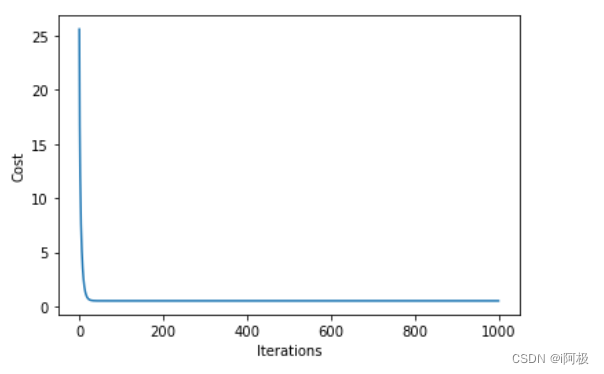
我们通过画图的方式展示了模型拟合的结果，同时也可以看到成本函数随着迭代次数的变化。

3、sklearn内置模块实现

下面是使用sklearn内置模块实现线性回归模型的梯度下降法的实战案例：
导入模块

from sklearn.linear_model import SGDRegressor
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

首先使用make_regression函数生成了一个模拟数据集，其中包含1000个样本，每个样本包含10个特征，噪声为10：

X, y = make_regression(n_samples=1000, n_features=10, noise=10)

然后使用train_test_split函数将数据集划分为训练集和测试集，其中测试集占20%：

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

接下来，使用SGDRegressor模型构建了一个梯度下降模型，并将alpha参数设置为0.1，learning_rate参数设置为’constant’，eta0参数设置为0.01，max_iter参数设置为1000：

sgd = SGDRegressor(alpha=0.1, learning_rate='constant', eta0=0.01, max_iter=1000)

然后，使用fit方法拟合了模型，并使用predict方法预测了测试集的结果：

# 拟合模型
sgd.fit(X_train, y_train)

# 预测
y_pred = sgd.predict(X_test)

最后，使用mean_squared_error函数计算了预测结果的均方误差:

# 计算均方误差
mse = mean_squared_error(y_test, y_pred)
print("mse:", mse)

需要注意的是，每次运行代码时，生成的模拟数据集都会不同，因此每次运行时计算的均方误差可能会不同。

---

📢文章下方有交流学习区！一起学习进步！💪💪💪
📢首发CSDN博客，创作不易，如果觉得文章不错，可以点赞👍收藏📁评论📒
📢你的支持和鼓励是我创作的动力❗❗❗