CMU 15-213 CSAPP (Ch1~Ch3)
CMU 15-213 CSAPP (Ch5~Ch7)
CMU 15-213 CSAPP (Ch8)
CMU 15-213 CSAPP (Ch9)
CMU 15-213 CSAPP (Ch10)
CMU 15-213 CSAPP (Ch11)
视频链接
课件链接
课程补充
该课程使用 64位 编译器!
Ch11. Dynamic Memory Allocation
11.1 Basic concepts
- 应用程序通过 Allocator ( 如 malloc ) 在 application 运行后指定 virtual memory size,获取 并 释放 “堆” ( Heap ) 中的 虚拟内存块;
- Allocator maintaiins the heap as a contiguous collection of blocks;
- ”已分配使用“
- ”已释放 待使用“;
- Allocators 主要分为两类:
- 显式 ( explicit ),如 C 语言中的 malloc 和 free,分配与释放 完全由 application 自行控制;
- 隐式 ( implicit ),如 Java、ML、Lisp 等,application 分配,但由 system 的 ”垃圾回收“ ( Garbage collection ) 释放内存;
11.1.1 The malloc Package
- Allocators in C is provided by standard C library, “malloc package”;
#include <stdlib.h>
void *malloc(size_t size);
void free(void *p);
void *calloc(size_t nmemb, size_t size);
void *realloc(void *ptr, size_t size);
void *reallocarray(void *ptr, size_t nmemb, size_t size);
#include <unistd.h>
int brk(void *addr);
void *sbrk(intptr_t increment);
/********** annotation **********/
brk() and sbrk() change the location of the program break, which defines
the end of the process's data segment (i.e., the program break is the first
location after the end of the uninitialized data segment). Increasing the
program break has the effect of allocating memory to the process; decreasing
the break deallocates memory.
brk() sets the end of the data segment to the value specified by addr, when
that value is reasonable, the system has enough memory, and the process does
not exceed its maximum data size (see setrlimit(2)).
sbrk() increments the program's data space by increment bytes. Calling sbrk()
with an increment of 0 can be used to find the current location of
the program break.
- void *malloc ( size_t size )
- 返回 void 指针,指向 至少 size 个字节的内存块;
- x86 块大小 8 字节对齐,x86-64 块大小 16 字节对齐;
//CentOS
#include <stdlib.h>
#include <stdio.h>
#include <unistd.h>
#include <math.h>
#include <errno.h>
#include <string.h>
int main()
{
void *pbrk0 = sbrk(0);
void *p1 = malloc(1);
void *pbrk1 = sbrk(0);
void *p2 = NULL;
for(int cnt=0;cnt<1000;cnt++) p2 = malloc(0);
void *pbrk2 = sbrk(0);
void *p3 = malloc(pow(10,10));
printf( "pbrk0 [%p]\n"
"p1 [%p]\n"
"pbrk1 [%p]\n"
"p2 [%p]\n"
"pbrk2 [%p]\n"
"p3 [%p]\n"
"errno [%d]\n"
"strerr [%s]\n",
pbrk0,p1,pbrk1,p2,pbrk2,p3,errno,strerror(errno));
return 0;
}
[root@localhost allo]# uname -a
Linux localhost.localdomain 4.18.0-240.el8.x86_64 #1 SMP Fri Sep 25 19:48:47 UTC 2020 x86_64 x86_64 x86_64 GNU/Linux
[root@localhost]# gcc a.c
[root@localhost]# ./a.out
pbrk0 [0xfda000]
p1 [0xfda2a0]
pbrk1 [0xffb000]
p2 [0xfe1fa0] // 0xfe1fa0 - 0xfda2a0 = 0x7d00 = 32 * 1000
pbrk2 [0xffb000] // 0xffb000 - 0xfda000 = 0x21000, 编译时就决定 “一次性移动一大步”
p3 [(nil)]
errno [12]
error [Cannot allocate memory]
- void free ( void *p )
- Returns the block pointed at by p to pool of available memory;
- p must come from a previous call to malloc、calloc ( 公开课上发音 “c” “alloc” ) or realloc;
11.1.2 How to implement malloc and free ?
- Assumption
- 内存 以 word 为最小单元编址,( on x86 ) word = 4 bytes;
- malloc、free 入参单位为 word;

- Constraints
- Application 调用 malloc 和 free 的顺序随机;
- free 的入参必须是 指向已分配内存块的 指针;
- 请求的 块大小 或 数量 不可控;
- 请求 必须立即响应 ( 不可以 囤一堆请求一次性响应,或 重排请求的先后顺序 ) ;
- 只能用 free memory 响应请求,一旦分配 allocators 再也无权访问;
- allocator can’t compress or smoosh them all together to create larger free blocks;
- 大小对齐 8-byte (x86) or 16-byte (x86-64);
- Performance Goal
Allocators combine a trade-off of both running time ( speed ) and space. So these speed and memory efficiency metrics are defined;- Troughput
Number of completed requests per unit time,eg:5000 malloc calls + 5000 free calls in 10 sec,throughput is 1000 ops/sec; - Peak Memory Utilization (
U
k
U_k
Uk )
U k = m a x ( ∑ i < k P i ) H k U_k=\frac{max( \sum\limits_{i<k}{P_i} )}{H_k} Uk=Hkmax(i<k∑Pi)
【Payload】malloc ( p ),result in a block with a payload of p bytes;
【Aggregate payload】 P k P_k Pk,the sum of currently allocated payload after request R 1 , R 2 . . . R k R_1,R_2 ... R_k R1,R2...Rk has completed;
【Current heap size】 H k H_k Hk;
- Troughput
- 实现一个 allocator 需要面对的问题 ( answers in implicit free list )
- How much memory to free given just a pointer ?
- How to keep track of the free blocks ?
- How to deal with extra space when requiring blocks smaller than free blocks it is placed in ?
- How to choose a specific block among so many free blocks ?
- How to reinsert freed blocks ?
11.1.3 Fragmentation
- Internal Fragmentation
- payload is smaller than block size;
- like padding for alignment,overhead for maintaining,explicit policy ( don’t want to splinter blocks up into little chunks );
- depends only on the pattern of previous requests,easy to measure;
- External Fragmentation
- aggregate heap memory is enough,but no single free block satisfied request;
- depends on the pattern of future requests,difficult to measure;

11.2 Implicit free lists
- Knowing How Much to Free
- standard method
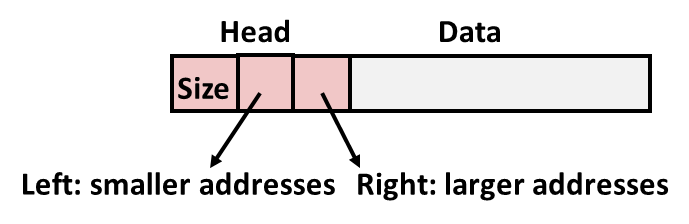
把 size 藏在 block 开头的的 word 中,这个 word 被称为 header field 或者 header;

- standard method
- Keeping Track of Free Blocks
- 【1】Implicit list
Traversing all free blocks in heap by traversing all blocks,ignoring allocated blocks;
There is no list of free blocks,but the headers in blocks can tell;
与 blocks 的总数线性相关;

- 【2】Explicit list
Use some of the words in the block to create singly or doubly linked lists;
与 free blocks 的总数线性相关,效率略有提升;

- 【3】Segregated free list
Different free lists for different size classes; - 【4】Blocks sorted by size
Use a balanced tree (e.g. Red-Black tree) with pointers and the length used as a key
- 【1】Implicit list
11.2.1 Implicit List
-
Each block needs size and allocation status,standard trick:
- Blocks has to be aligned,low-order bits are always 0,use it as a allocated / free flag;
- Must mask out this bit when read size of blocks;
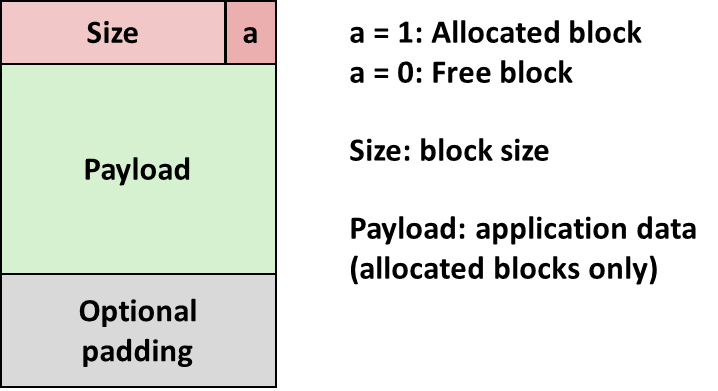
- 例子

payload 的起始地址要求 2字对齐,导致 block size 2字对齐,header 在当前 payload 的前一个word;最后,留一个 0 size block 标志 heap 的结尾(合并 free blocks 时消除特殊情况);
-
Finding a Free Block
- 【First Fit】Search from beginning,choose first free block that fits;It can cause “splinters” at beginning of list;Take linear time in total number of blocks;
void *search_free_block(int len) { void *p = list.begin(); alloc = (*p & 1); // 是否被分配 tsize = (*p & -2); // free block 总大小 (Byte) psize = tsize - 4; // max_payload = tsize - header_size (Byte) while( p<list.end() && (alloc || psize<len)) //已被分配 或 大小不满足请求 p = p + tsize/4; //next block (word addressed) return p; }- 【Next Fit】Search from where previous search finished;Obviously faster than first fit ( avoid re-scanning unhelpful blocks );fragmentation maybe worse;
- 【Best Fit】Search list and choose the best free block ( closest to size required ) ;less fragmentation but slower than first fit;infinite segregated free list is one way to approach best fit;
-
Allocating in Free Block
- Split the block if size required is smaller than free block,or just return the whole block ?

- Split the block if size required is smaller than free block,or just return the whole block ?
void addblock(void *p, int len)
{
// arithmetic shift, round up to even(远零取整),两字节对齐
int newsize = ((len + 1) >> 1) << 1;
int oldsize = *p & -2; // mask out status bit
*p = newsize | 1; // set length and allocted status of new block
if (newsize < oldsize) // set length of remaining free block
*(p + newsize) = oldsize - newsize;
}
void * malloc(int len)
{
void *p = NULL;
p = search_free_block();
if(p) addblock(p,len + 4); // header size = 4 Bytes
return p + 1; // (p + 4 bytes) addresse of payload
}
- Freeing a Block
- only clear “allocated” status ? Generating external fragmentation !!
- Adjacent free blocks need to be coalesced
- All decent allocator is that contiguous free blocks never exist;

void free_block(ptr p)
{
*p = *p & -2; // clear allocated flag
next = p + (*p)/4; // find next block header
if ((*next & 1) == 0) // if not allocated
*p = *p + *next; // add to this block
}
- How to Coalescing previous block
- remember the previous block while traverse the list,very inefficient !
- Bidirectional Coalescing
- Boundary tags [ Don Kunth 1973 ];
Replicate header at end of free blocks ( a.k.a. “footer” ),这样 free§ 的时候,p-1 便是 前一个 block 的 “footer”(即 “header”),从而判断是否与前一个 block 进行 Coalescing;缺点是 overhead 变大;

4 cases:
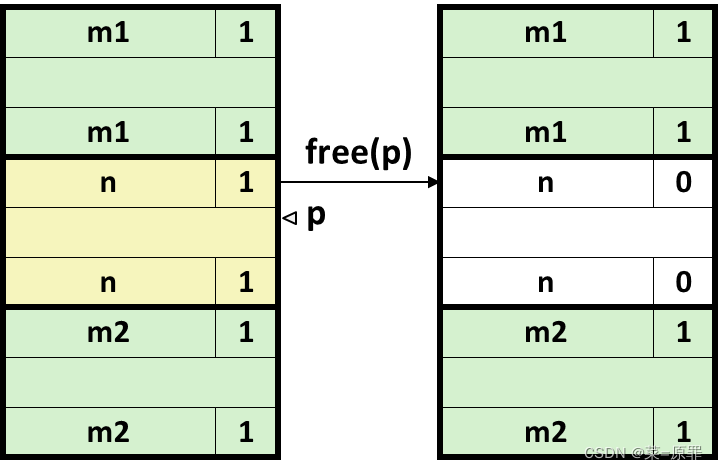
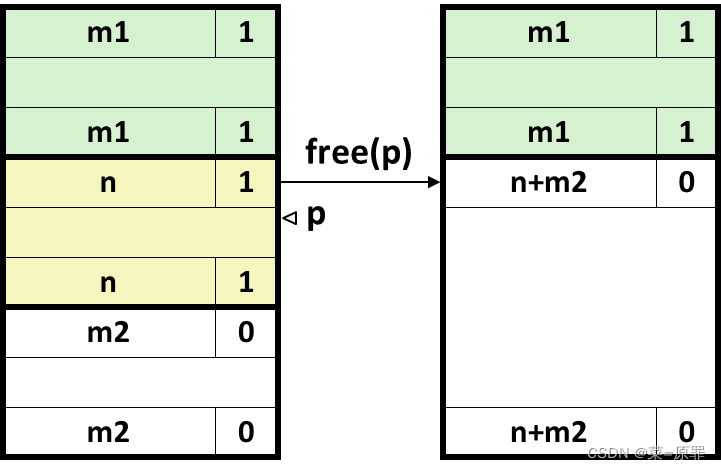


- Boundary tags [ Don Kunth 1973 ];
Allocated block 都没有 footer;怎样才能在没有 footer 的条件下判断 previous block 是否 allocated ?
如果 previous block 是 allocated 状态,则它不参与合并,footer也就没有存在的必要 !!
但没有 “footer” 又不能判断 previous block 是否被 allocated,怎么办?
字节对齐导致 header 的低 n 位都是 0 !
malloc 时在其 后 一个 header 中用一个 低位记录 “allocated” 状态;
11.3 Explicit free lists
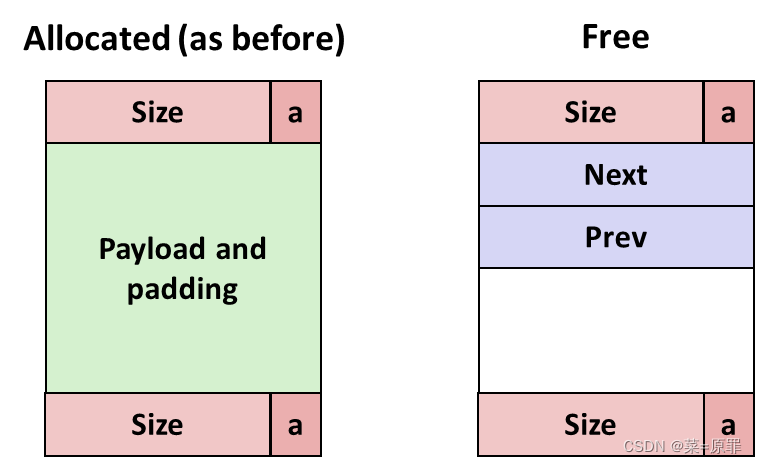
Implicit Free List 是由 block 的 length 隐式构建的单向链表,链表节点在虚拟地址上也是连续的;
而 Explicit 则是由 指针 显式构建的双向链表,链表节点间的相对位置随机;
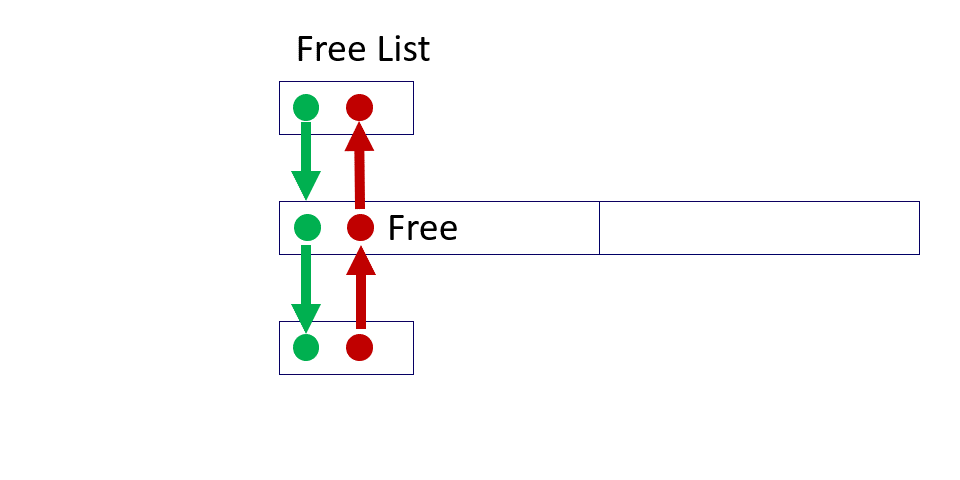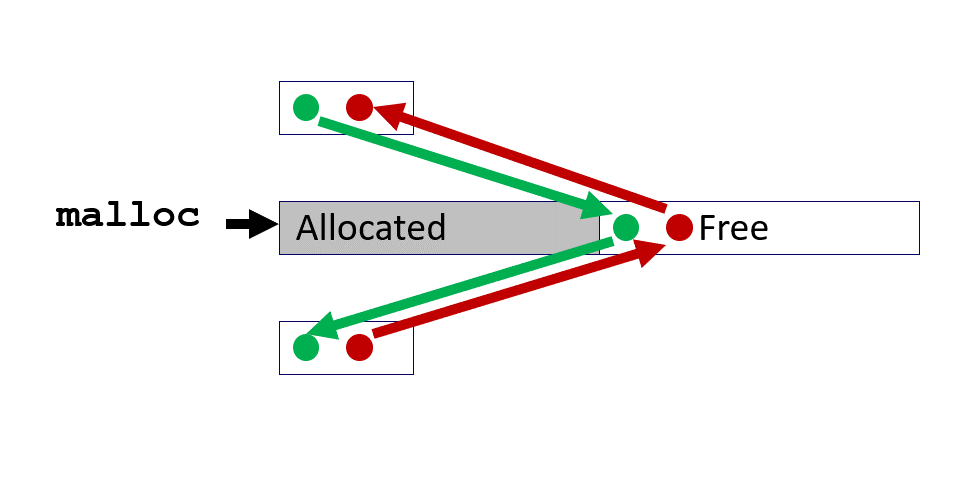
11.3.1 Allocating
只需要更新 4个指针;
11.3.2 Freeing
核心问题:Where to insert the newly freed block ?
- LIFO (last - in - first - out) Policy
- free list 的开头插入新释放的 block;
- 实现简单,时间复杂度 O(1);
- 研究表明 碎片较 Address-ordered 更多;
- Address-ordered Policy
- pre 块地址 < newly freed 块地址 < next 块地址;
- 需要 search,可以通过 平衡树 等方法加速;
- 碎片较少;
很多程序员会犯 过早优化 ( premature optimization ) 的错误,刚开始就思考奇奇怪怪的场景和对应的优化措施;在解决 allocator 这样复杂的问题的时候,应该本着“先易后难” 的原则,先有基础方案,再找瓶颈 并 逐个优化;
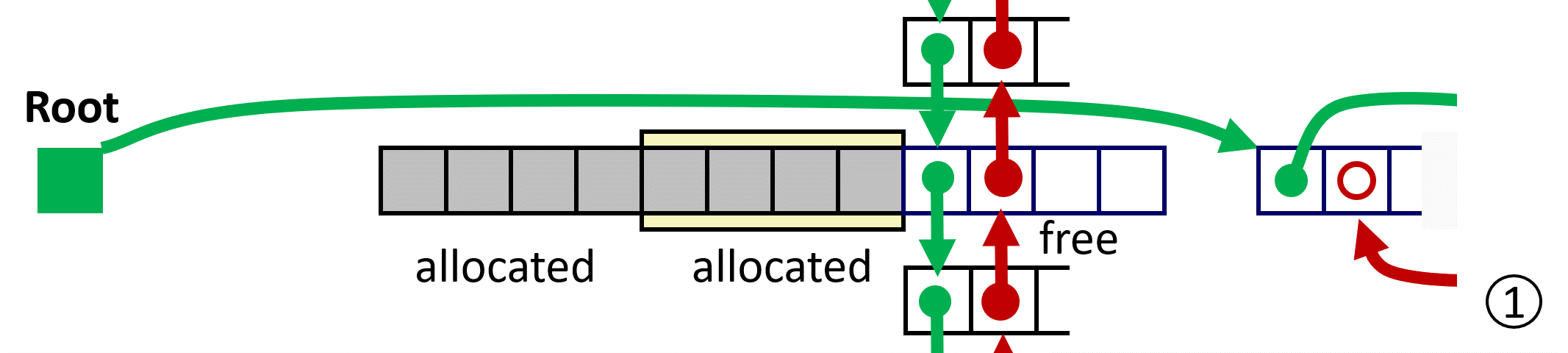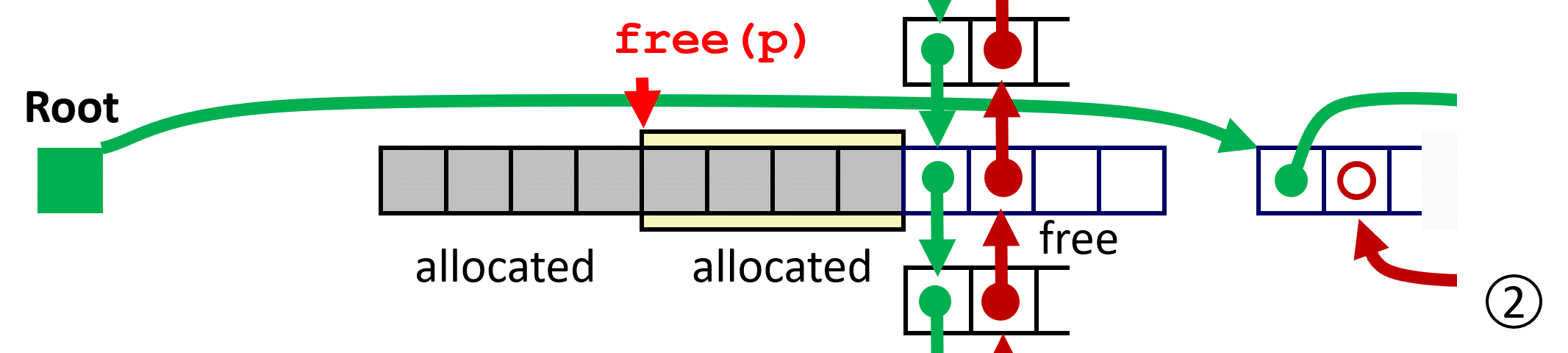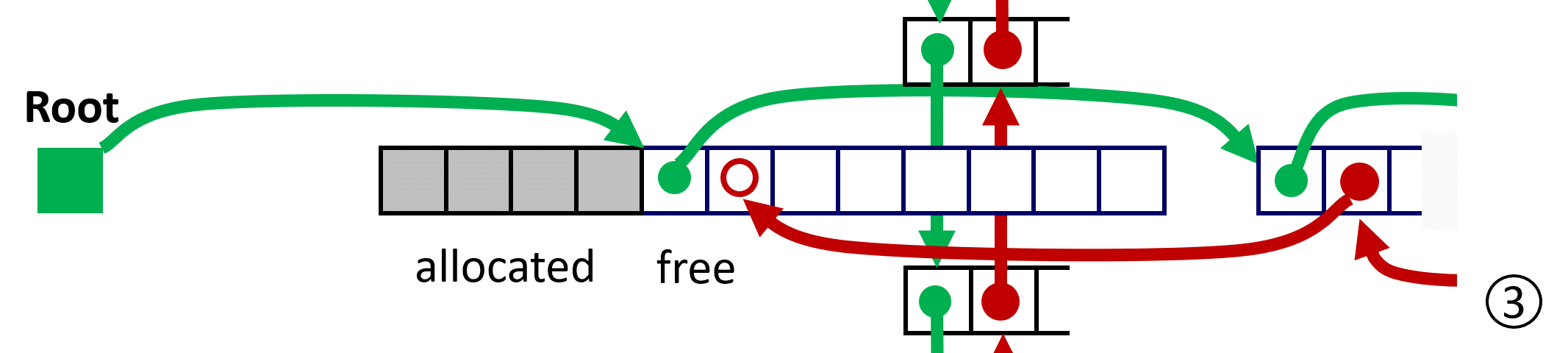
为方便描述,使用 predecessor 和 successor 分别表示 虚拟地址(VA)前后相邻,而用 prev 和 next 表示 free list 中的前后相连;
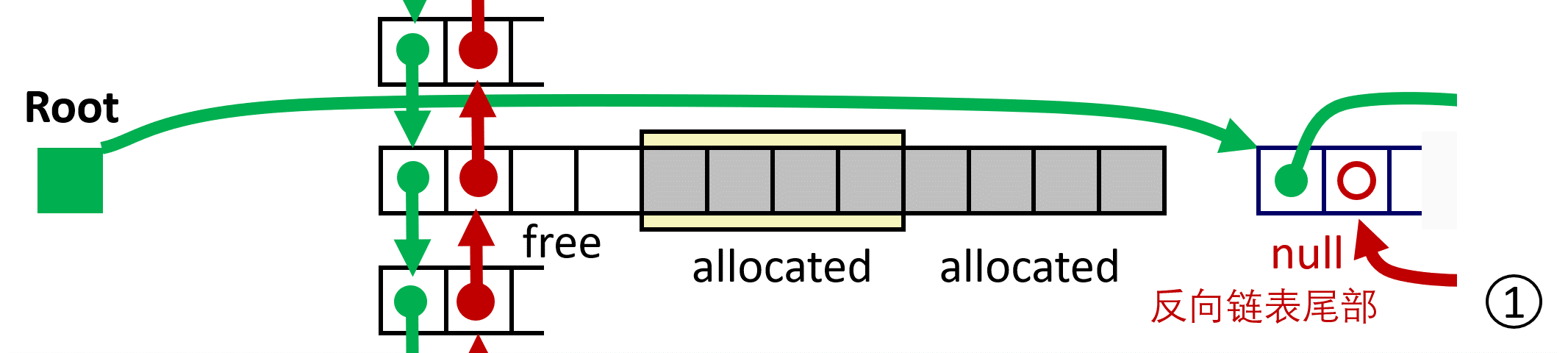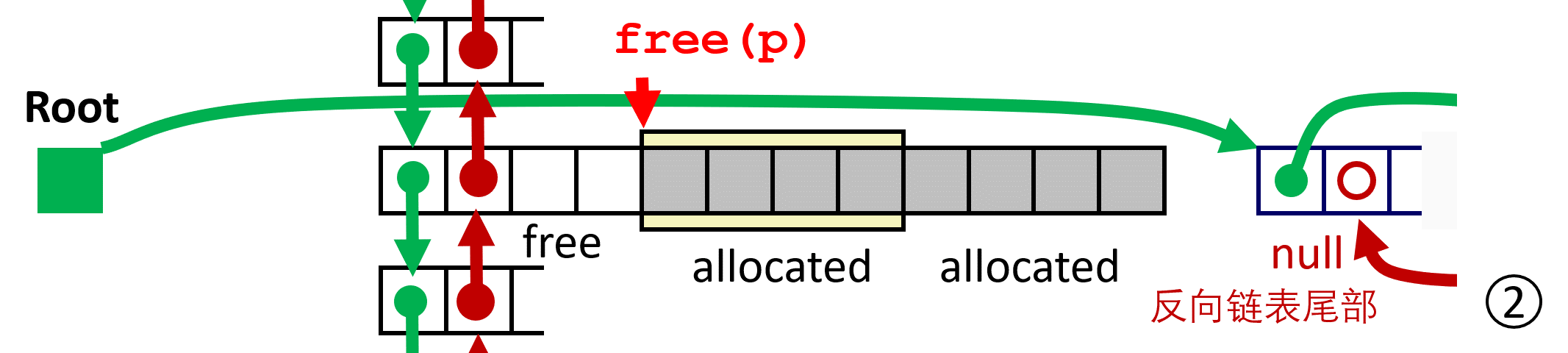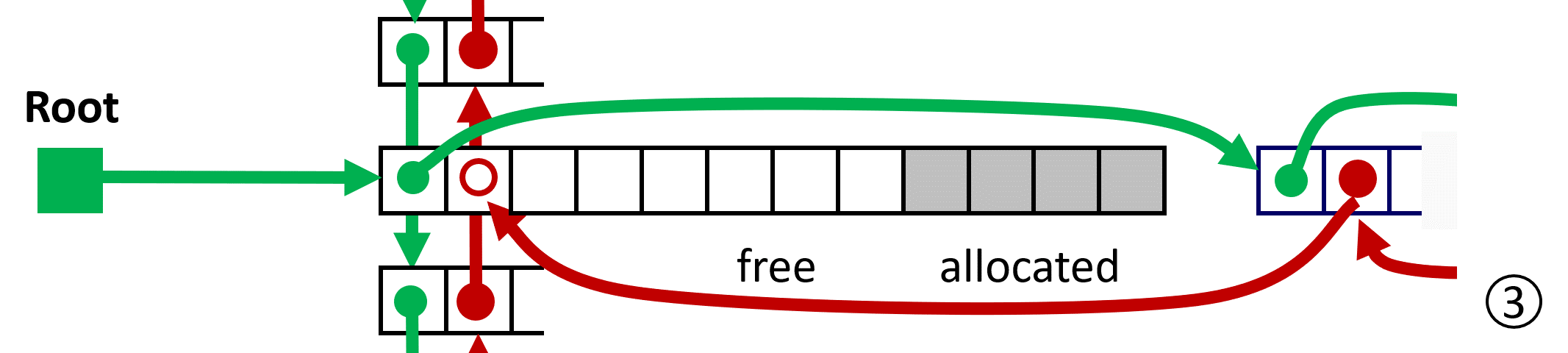
LIFO Case 1 前后都不用 coalescing;
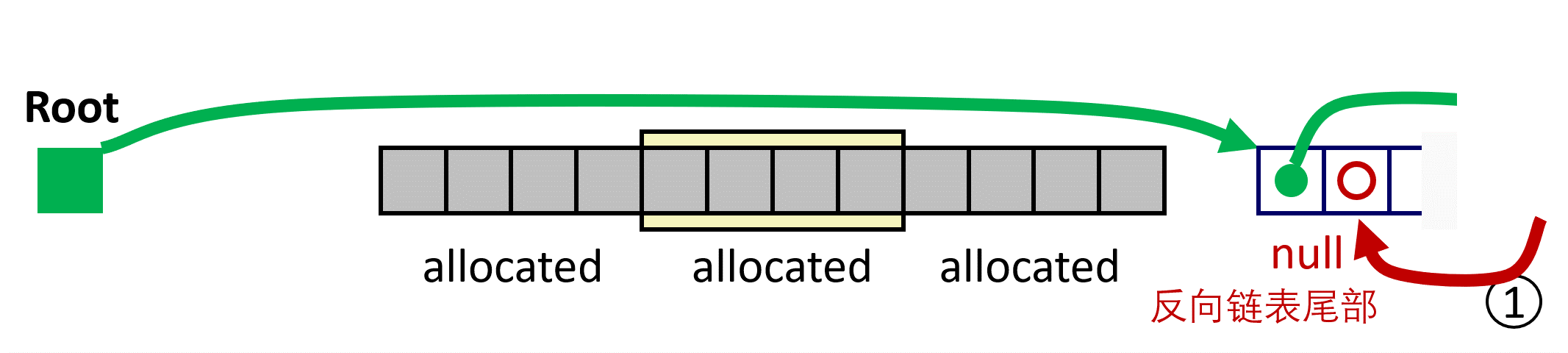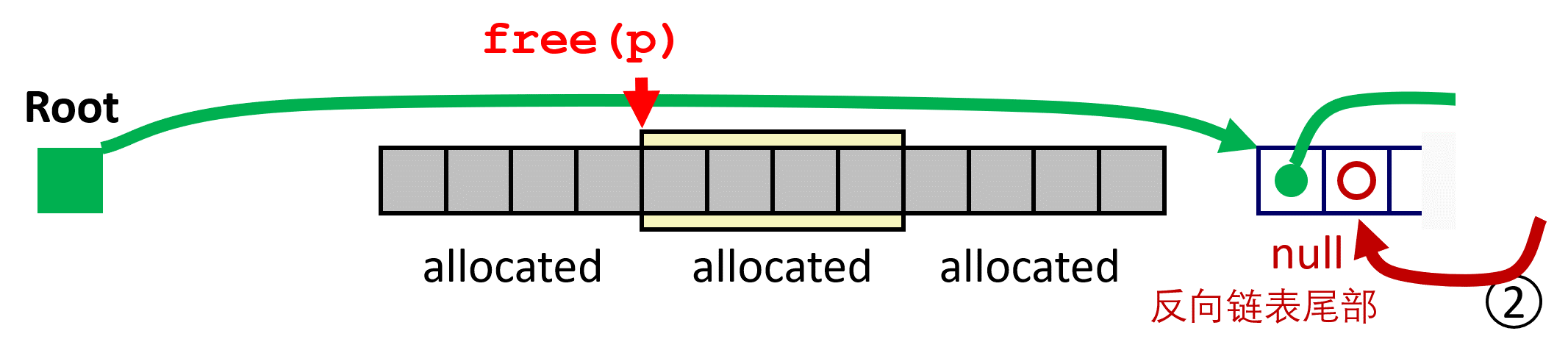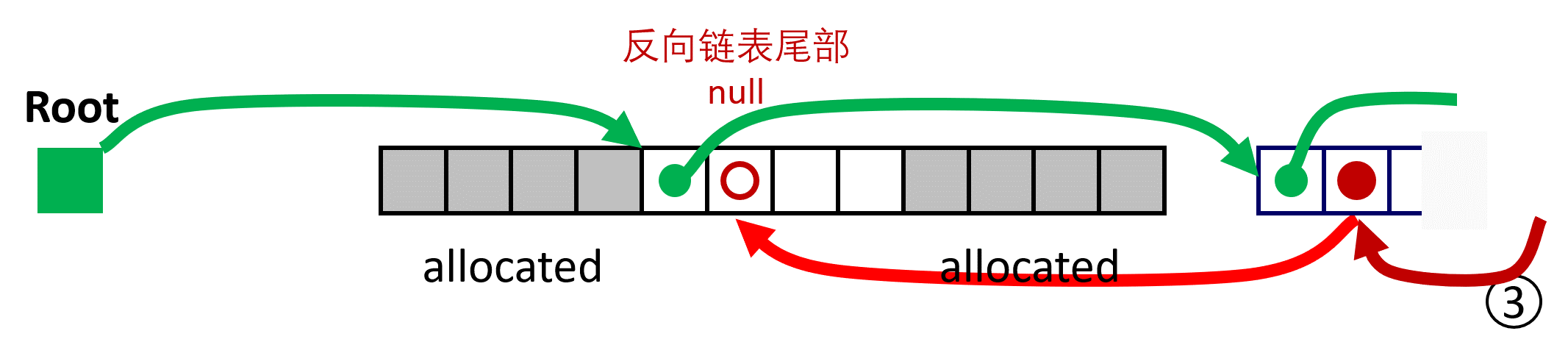
LIFO Case 2 与 predecessor 进行 coalescing;
LIFO Case 3 与 successor 进行 coalescing;
LIFO Case 4 与 successor、predecessor 同时 coalescing;
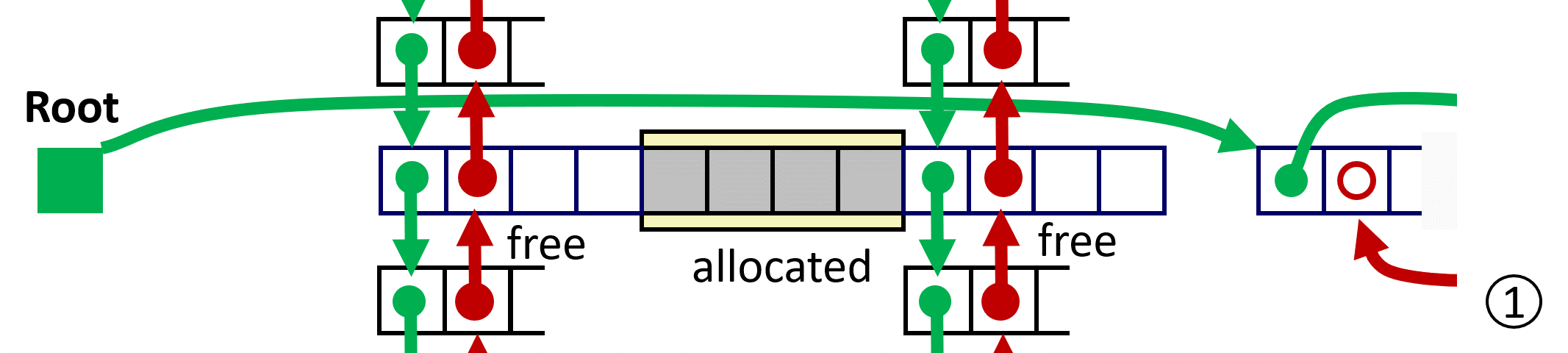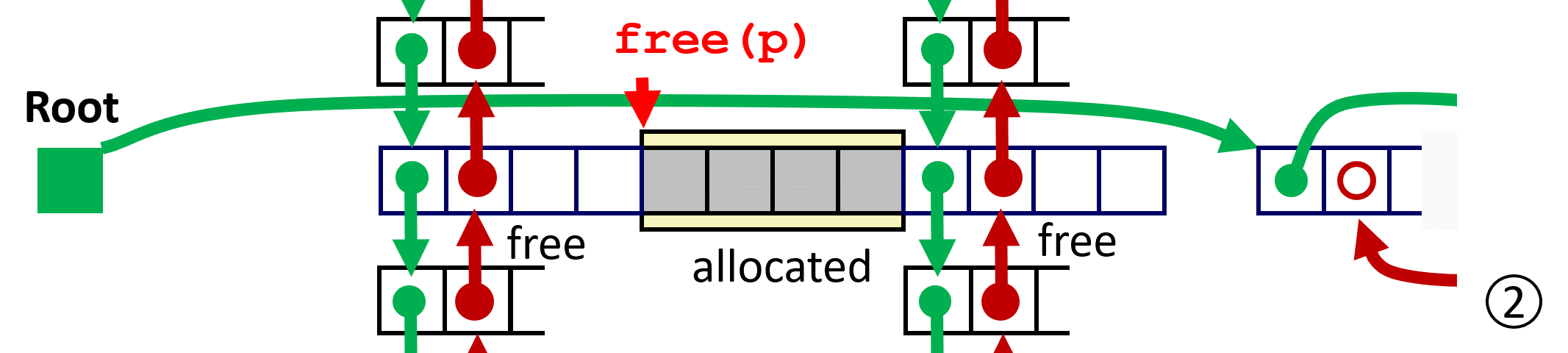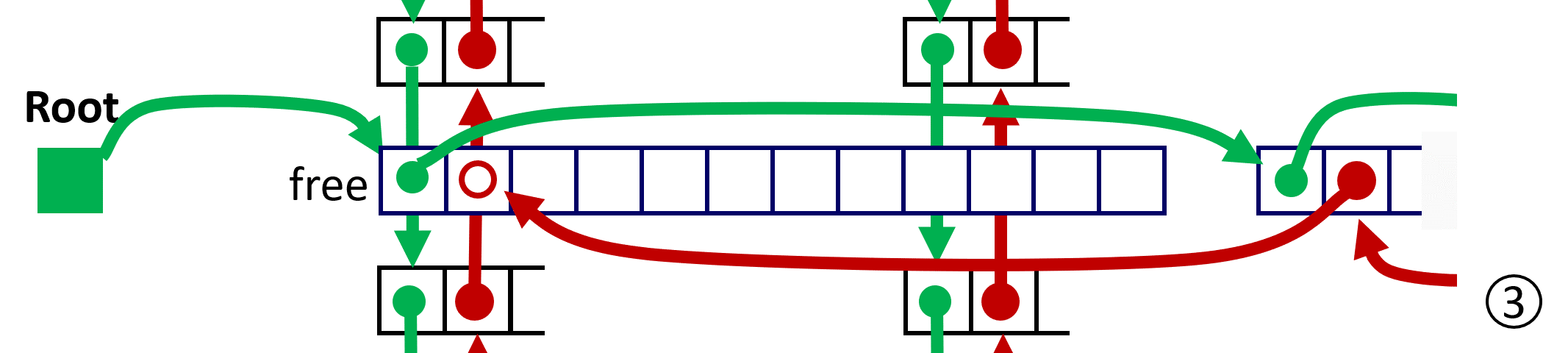
11.3.3 Explicit List Summary
- v.s. Implicit List
- Faster,seaching free list only instead of whole heap ( especially when most of the memory is full );
- More complicated splicing business;
- Extra space for linked list pointers;
11.4 Segregated free lists
Each size class has its own free list;

-
To allocato a block of size n:
- Seach appropriate free lists of blocks of requiring size m ( If the block is not found, try next larger class );
- Place split block on appropriate list ( optional, may be class size exactly equal to the requiring size )
- If no block is found:
- Request additional heap memory from OS ( sbrk() );
- Allocate block of n bytes from this new memory;
- Place remainder (剩余的块) as a single free block in largest size class;
-
To free a block;
- Coalesce (like before) and place on appropriate list;
-
Advantages of seglist allocators
- Higher throughput,快:
二分查找 合适大小的空闲块链表,log time for power-of-two size classes; - Better memory utilization,省:
对 seglist 的 First-fit search 几乎等效于 对整个 heap 进行了 best-fit search;
- Higher throughput,快:
sbrk 是 Syscall,花费约几百微妙,overhead 很大,通过 一次 sbrk 申请一个超大块的方式,amortize (均摊) 时间开销;但同时,memory utilization 将变得很低;又一个 space – time trade – off
Seglist 存放在 heap 的起始位置 (见 malloc Lab);
More read:
“Dynamic Storage Allocation: A Survey and Critical Review”
11.5 Implicit Memory Management: Garbage Collection
- Automatic reclamation of heap-allocated storage;
- Common in many dynamic languages;
Python, Ruby, Java, Perl, ML, Lisp, Mathematica; - Variants (“conservative” garbage collectors) exist for C and C++
Allocator can’t determine whether these blocks are indeed garbage;
void foo(){
int *p = malloc(128); // garbage
return;
}
11.5.1 Garbage Collection
- Which memory can be freed?
- 扫描内存,辨别指针及被其指向的块,没有被指向的块,认为是 Garbage;
- Assumptions about pointers
- Memory Manager 需要能分辨出哪些变量是指针;
- 假设 指针都指向 块的开头(反例如 指向数组中元素的指针);
- 指针必须是静态不可变的?
- Classical GC Algorithms
- Mark-and-sweep collection (McCarthy, 1960)
- Reference counting (Collins, 1960)
- Copying collection (Minsky, 1963)
- Generational Collectors (Lieberman and Hewitt, 1983)
- Collection based on lifetimes;
- Most allocations become garbage very soon;
- So focus reclamation work on zones of memory recently allocated;
More information “Garbage Collection: Algorithms for Automatic Dynamic Memory”, John Wiley & Sons, 1996.
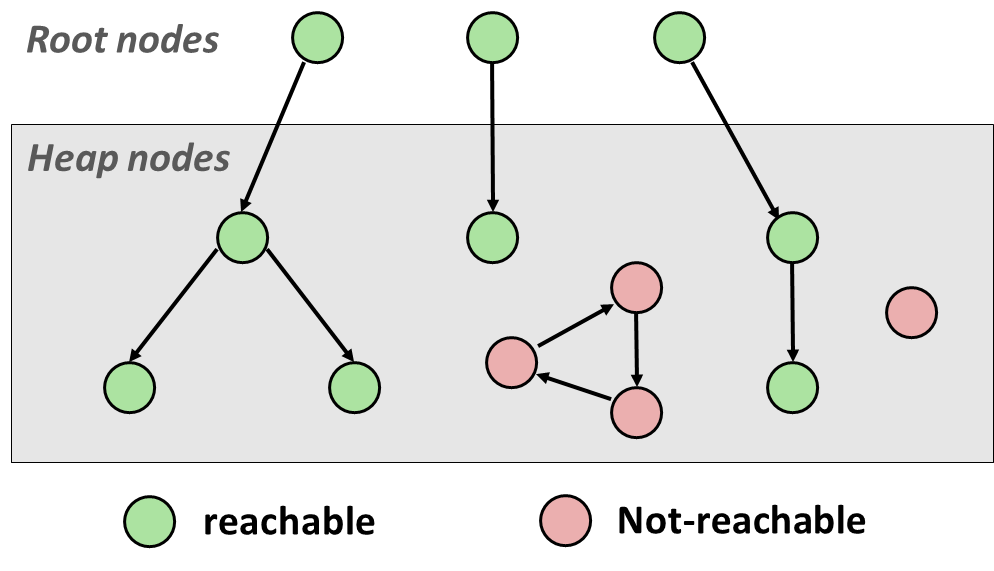
- Mark-and-sweep collection
- Each block is a node in graph;
- Each pointer is a edge in the graph;
- Locations not in the heap that contain pointers into the heap are calld root nodes (e.g. registers, locations on the stack, global variables);
- A node is reachable if there is a path from any root to that node;
Non-reachable nodes are garbage;
- Implement on top of malloc / free package
- Allocate using malloc until you “run out of space”;
- When out of space,use extra mark bit in the head of each block;
- Sub phase 1,mark,start from all roots and set mark bit on each reachable block( depth-first traversal );
- Sub phase 2,scan all blocks,and free blocks that are not marked;
- A Simple Implementation
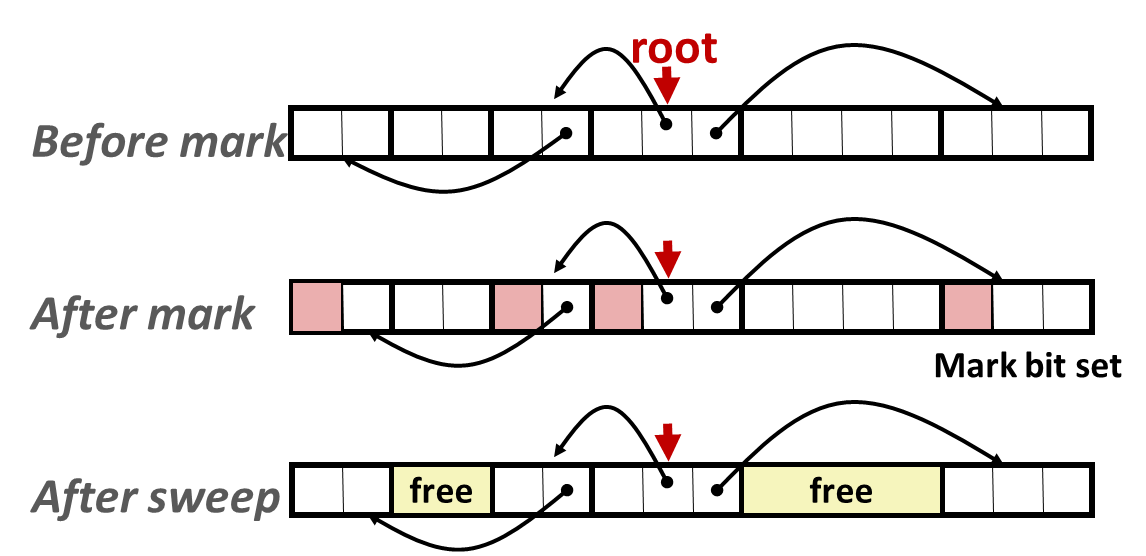
ptr mark(ptr p) // pointer to the payload
{
if (false == is_ptr(p)) return; // do nothing if not pointer
if (true == markBitSet(p)) return; // check if already marked
setMarkBit(p); // set the mark bit
for (i=0; i < length(p); i++) // mark() recursively
mark(p[i]);
return;
}
ptr sweep(ptr p, ptr end)
{
while (p < end) // scan the whole heap
{
if(true == markBitSet(p)) clearMarkBit(); // 正在被引用的块
else if (true == allocateBitSet(p)) free(p); // 没有被引用的块
p += length(p); // 将 p 指向 next block
}
- How to find the beginning of the block
- In C,pointers can point to the middle of a block;
- Use a balanced binary tree to keep track of all allocated blocks (key is start-of-block);
- Balanced-tree pointers can be stored in header (use two additional words);
- Search the binary tree,a pointer should fall in the beginning and end of some allocated block,and that block is reachable;
- It’s conservative,because it maybe just an integer,but purportedly points to non-reachable blocks;
11.6 Memory-related perils and pitfalls
Errors involving memory are the worst kind of bugs to try to find out,because they are distant in both space and time;You only find out about those errors when you try to reference that data;
- Dereferencing bad pointers
- Reading uninitialized memory
- Overwriting memory
- Referencing nonexistent variables
- Freeing blocks multiple times
- Referencing freed blocks
- Failing to free blocks
C pointers,只要根据声明时 运算符的优先级,就不会认错类型;
| declarations | type of p |
|---|---|
| int *p | pointer to int |
| int *p[13] | an array[13] of pointer to int |
| int *(p[13]) | an array[13] of pointer to int |
| int (*p)[13] | a pointer to an array[13] of int |
| int (*(*f())[13])() | a function returning ptr to an array[13]of pointers to functions returning int |
| int (*(*x[3])())[5] | an array[3] of pointers to functions returning pointers to array[5] of ints |
*x[3],[]优先级高,x 是 size 为 3 的数组,其左是*,数组的元素是指针;
*(*x[3])(),数组元素(指针)指向函数,函数的返回值也是指针;
int (*(*x[3])())[5],函数返回的指针,指向 size 为 5 的 int 数组;