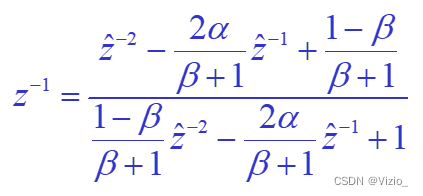【POJ No. 3067】 公路交叉数 Japan
北大 OJ 题目地址
【题意】
东海岸有N 个城市,西海岸有M 个城市(N ≤1000,M ≤1000),将建成K 条高速公路。每个海岸的城市从北到南编号为1, 2, ……每条高速公路都是直线,连接东海岸的城市和西海岸的城市。建设资金由高速公路之间的交叉数决定。
两个高速公路最多在一个地方交叉。请计算高速公路之间的交叉数量。
【输入输出】
输入:
输入文件以T 为开头,表示测试用例的数量。每个测试用例都以3个数字N 、M 、K 为开头。下面K 行中的每一行都包含两个数字,表示由高速公路连接的城市号。
第1个是东海岸的城市号,第2个是西海岸的城市号。
输出:
对每个测试用例,都单行输出“Test case x : s ”,x表示输入样例编号,s 表示交叉数。
【样例】

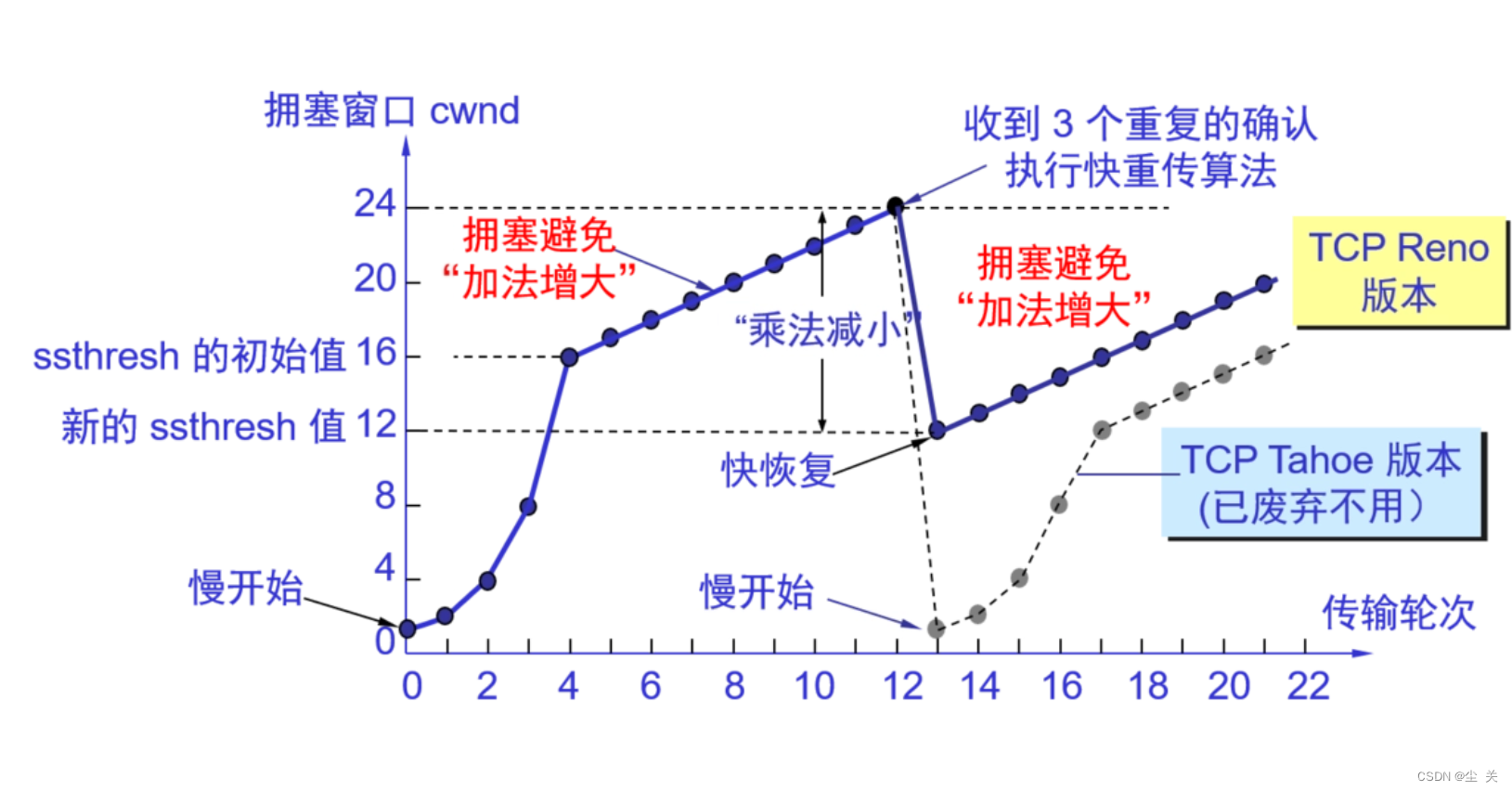
【思路分析】
根据输入样例分析,一共有5个交叉点。

那么,怎么求交叉点呢?首先搞清楚交叉点是怎么产生的。当两条边的城市号都以升序(或降序)形式出现时,不产生交叉点。例如1 2和2 3不会产生交叉点

1 4和2 3会产生交叉点,因为西海岸城市1、2是升序的,东海岸城市4、3是降序的。

因此交叉点的产生原因和逆序对有关系,所以转变为求解逆序对问题。
【算法设计】
① 对输入的边按照x 升序排列,若x 相等,则按y 升序排列。
② 检查每条边i ,统计y 的前缀和sum(e[i ].y ),该前缀和是前面比y 小的正序数,边数减去正序数,即可得到逆序数i -sum(e[i].y ),ans累加逆序数。
③ 将树状数组中e[i ].y 的值加1。
【举个栗子】
根据输入样例,其交叉点求解过程如下。
① 对输入的边按照x 升序,若x 相等,则按y 升序。
排序结果:

② 按照排序结果检查每条边i ,统计y 的前缀和sum(e[i ].y),将ans累加i -sum(e[i ].y )。
-
i =0:1 4=。sum(4)0,i -sum(4)=0;1的前缀和为0,说明1前面没有数,因为前面还没有输入边,所以逆序边数量ans=0。
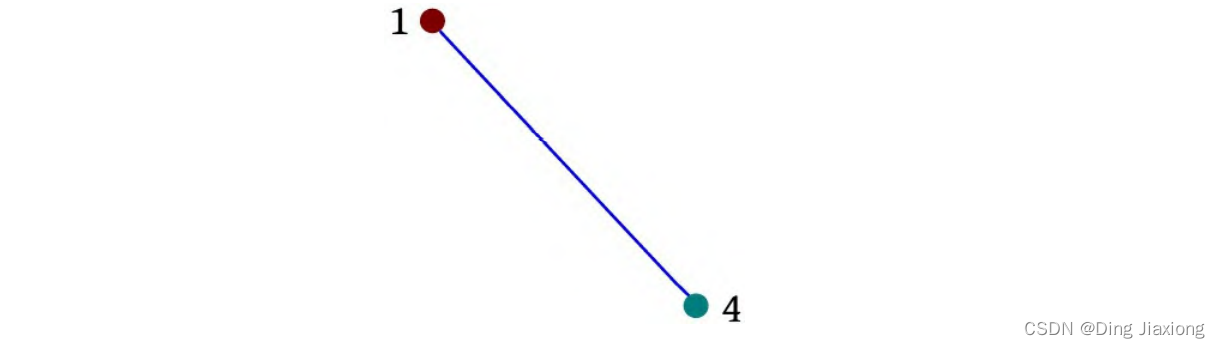
-
i =1:2 3。sum(3)=0,i -sum(3)=1。3的前缀和为0,说明3前面没有数,所以前面的1条边是逆序的,当前边和逆序边会产生交叉点,累加逆序边数量ans=1。
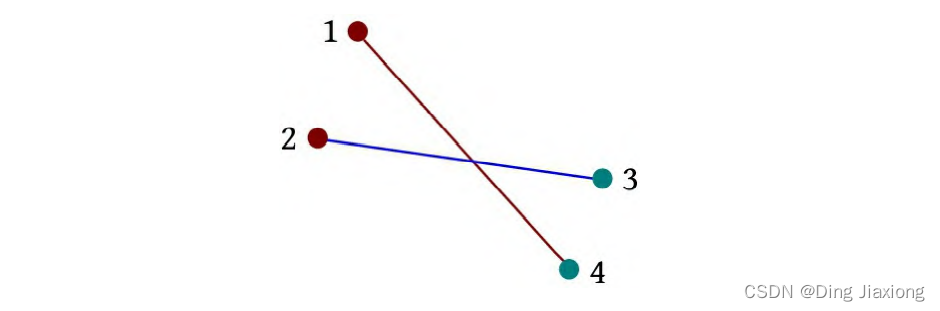
-
i =2:3 1。sum(1)=0,i -sum(1)=2。1的前缀和为0,说明1前面没有数,因此前面的两条边是逆序的,当前边和每条逆序边会产生交叉点,累加逆序边数量ans=3。
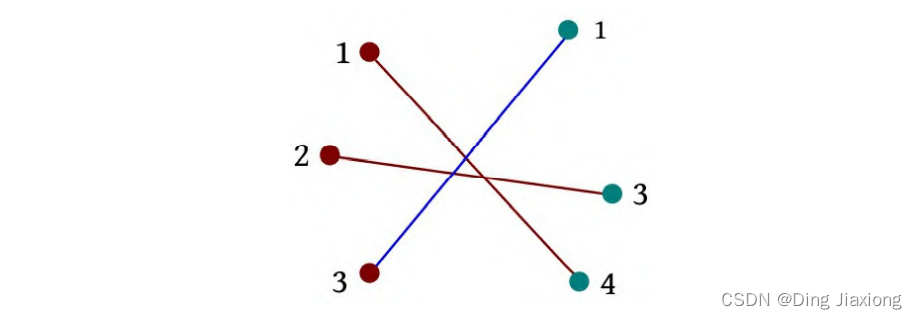
-
i =3:3 2。sum(2)=1,i -sum(2)=2;前面的3条边已经有1条边是正序的,将该边减去,其余两条边是逆序的,当前边和每个逆序边都会产生交叉点,累加逆序边数量ans=5。
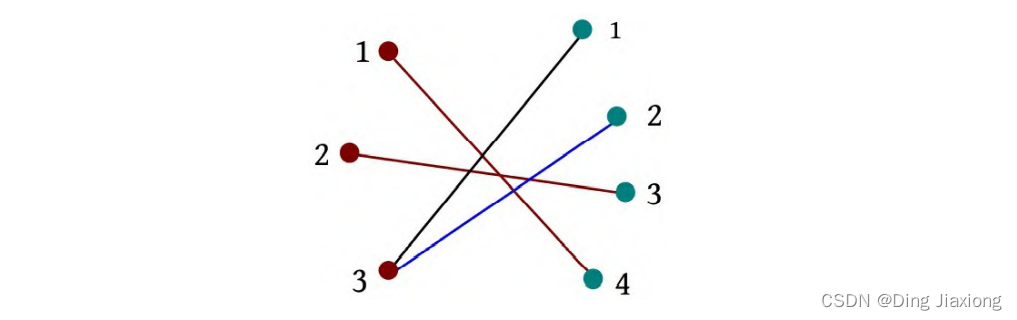
【算法实现】
#include<cstdio>
#include<cstring>
#include<algorithm>
#define maxn 1010
#define maxk 1000010
#define lowbit(x) (x)&(-x)
int c[maxn],kas,n,m,k;
using namespace std;
typedef long long LL;
struct Edge {
int x, y;
}e[maxk];
bool cmp(Edge a,Edge b)
{
return a.x<b.x||(a.x==b.x&&a.y<b.y);
}
void add(int i)//加1操作,参数省略
{
while(i<=m)//y点有m个
{
++c[i];
i+=lowbit(i);
}
}
int sum(int i)
{
int s=0;
while(i>0)
{
s+=c[i];
i-=lowbit(i);
}
return s;
}
int main()
{
int T;
scanf("%d",&T);
while (T--)
{
memset(c,0,sizeof(c));
scanf("%d%d%d",&n,&m,&k);
for(int i=0;i<k;i++)
scanf("%d%d",&e[i].x,&e[i].y);
sort(e,e+k,cmp);
LL ans=0;
for(int i=0;i<k;i++){
ans+=i-sum(e[i].y);
add(e[i].y);
}
printf("Test case %d: %lld\n",++kas,ans);
}
return 0;
}