💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码、数据、文章讲解

---

💥1 概述

文献来源：

摘要： 为了提高用于电力系统动态状态估计的无迹卡尔曼滤波（UKF）的数值稳定性，该文提出一种保证正半定估计误差协方差的新型UKF（UKF-GPS），并与现有的5种方法进行了比较，包括UKF-schol、UKF-GPS。κ， UKF 修改， UKF-ΔQ和平方根 UKF （SR-UKF）。这些方法和扩展卡尔曼滤波器（EKF）通过在WSCC 3机9总线系统和NPCC 48机140总线系统上执行动态状态估计来测试。对于WSCC系统，所有方法都能获得良好的估计。然而，对于NPCC系统，EKF和经典的UKF都失败了。发现UKF-schol，UKF-κ和 UKF-ΔQ在某些估计中效果不佳，而 UKF-GPS 在大多数情况下效果很好。UKF改性和SR-UKF始终可以很好地工作，这表明它们具有更好的可扩展性，这主要是由于增强了数值稳定性。

原文摘要：

Abstract:

In this paper, in order to enhance the numerical stability of the unscented Kalman filter (UKF) used for power system dynamic state estimation, a new UKF with guaranteed positive semidifinite estimation error covariance (UKF-GPS) is proposed and compared with five existing approaches, including UKF-schol, UKF- κ , UKF-modified, UKF- ΔQ , and the square-root UKF (SR-UKF). These methods and the extended Kalman filter (EKF) are tested by performing dynamic state estimation on WSCC 3-machine 9-bus system and NPCC 48-machine 140-bus system. For WSCC system, all methods obtain good estimates. However, for NPCC system, both EKF and the classic UKF fail. It is found that UKF-schol, UKF- κ , and UKF- ΔQ do not work well in some estimations while UKF-GPS works well in most cases. UKF-modified and SR-UKF can always work well, indicating their better scalability mainly due to the enhanced numerical stability.

状态估计是能源管理系统（EMS）的重要应用。然而，广泛研究的静态状态估计[2]-[8]假设电力系统在准稳态下运行，基于该稳态，系统的静态状态，即所有总线的电压幅度和相位角，通过使用监督控制和数据采集（SCADA）和/或相量测量单元（PMU）测量来估计。

静态状态估计对于电力系统监控非常重要，还为 EMS 中的其他重要应用提供输入数据，例如自动发电控制 （AGC） 和最佳潮流 （OPF）。然而，对于良好的系统监控和态势感知来说，这可能是不够的，因为电力系统变得更加动态，因为可再生能源发电的渗透率越来越高，具有非常高的不确定性和变化。因此，通过高级PMU部署促进的实时动态状态估计（DSE）获得的准确系统动态状态变得至关重要。凭借高全球定位系统（GPS）同步精度，PMU能够以高采样率提供高度同步的电压和电流相量测量，从而在实现实时广域监测、保护和控制方面发挥关键作用。

电力系统DSE已由不同类型的卡尔曼滤波器实现。卡尔曼滤波器 （KF） [9] 在非线性系统中最常见的应用是扩展卡尔曼滤波器 （EKF） [10]， [11] 的形式，它线性化所有非线性变换，并用雅可比矩阵代替 KF 方程中的线性变换，基于所有变换都是准线性的假设。电力系统DSE已由EKF [12]，[13]实现。

尽管EKF保持了KF优雅且计算高效的递归更新形式，但由于非线性函数的一阶泰勒级数近似[14]，它仅在“温和”非线性环境中运行良好。它是次优的，很容易导致背离。只有当误差传播可以用线性函数很好地近似时，线性化变换才是可靠的。此外，线性化只有在雅可比矩阵存在时才可以应用。即使 Jocobian 矩阵存在，计算它也可能是一个困难且容易出错的过程。

无迹变换（UT）[15]旨在通过提供更直接和明确的机制来转换均值和协方差信息来解决线性化的缺陷。基于UT，Julier等人。 [16]–[18]在状态估计的框架内提出了无迹卡尔曼滤波器（UKF）作为EKF的无导数替代品。UKF已应用于电力系统DSE，不需要线性化或计算雅可比矩阵[19]，[20]。然而，在[19]和[20]中，UKF仅用于估计单机无限总线系统或WSCC 3机器系统的动态状态。

毫不奇怪，UKF尚未应用于更大的电力系统。正如在[14]和[21]中指出的那样，EKF和UKF都可能遭受维数的诅咒，并且在状态向量大小为<>或更大的高维状态空间模型中，维数的影响可能会变得有害，特别是当描述状态空间模型的方程中存在高度非线性时，电力系统正是这种情况。

因此，即使经典 UKF 对小型系统具有良好的性能，也可能根本不适用于大型电源系统。我们将证明，数值稳定性主要限制了经典 UKF 的可扩展性。具体来说，当估计误差协方差传播时，它有时无法保持正半定性，从而使其平方根无法计算。

在本文中，我们介绍并比较了六种可用于增强UKF数值稳定性的技术，包括EKF / UKF工具箱方法[22]，正确设置无迹变换参数[23]，改进的UKF方法[17]，添加额外的正定矩阵[24]，[25]，本文提出的具有保证正半定估计误差协方差的UKF（UKF-GPS）和平方根UKF（SR-UKF）[26]。

本文的其余部分组织如下。第二节简要介绍了无味变换和经典的UKF程序。第三部分讨论了增强经典UKF数值稳定性的六种技术。第四节解释了如何实现卡尔曼滤波器进行电力系统动态状态估计。第五节在WSCC三机3总线系统和NPCC9机48总线系统上测试了所提出的方法。最后在第六节中得出结论。

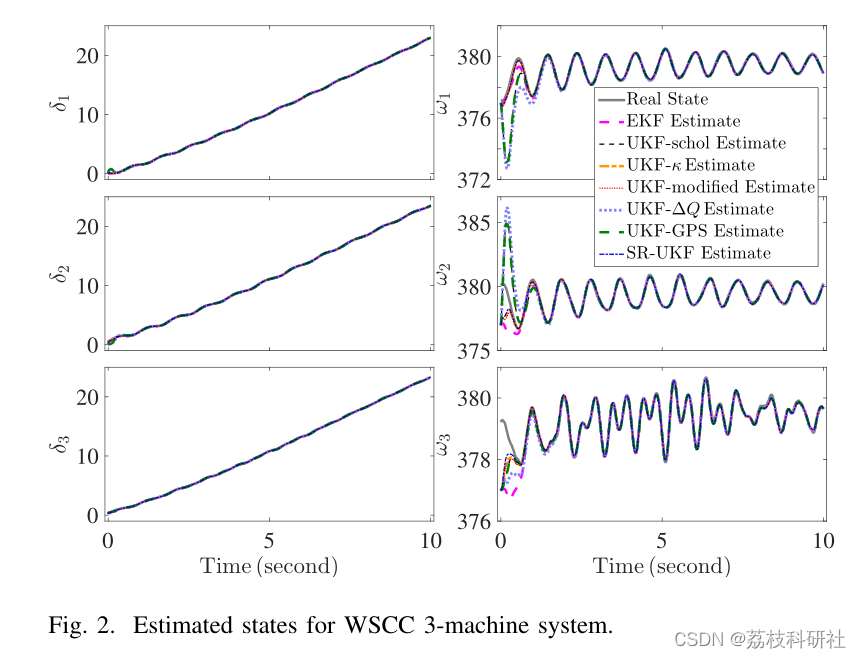
📚2 运行结果

 

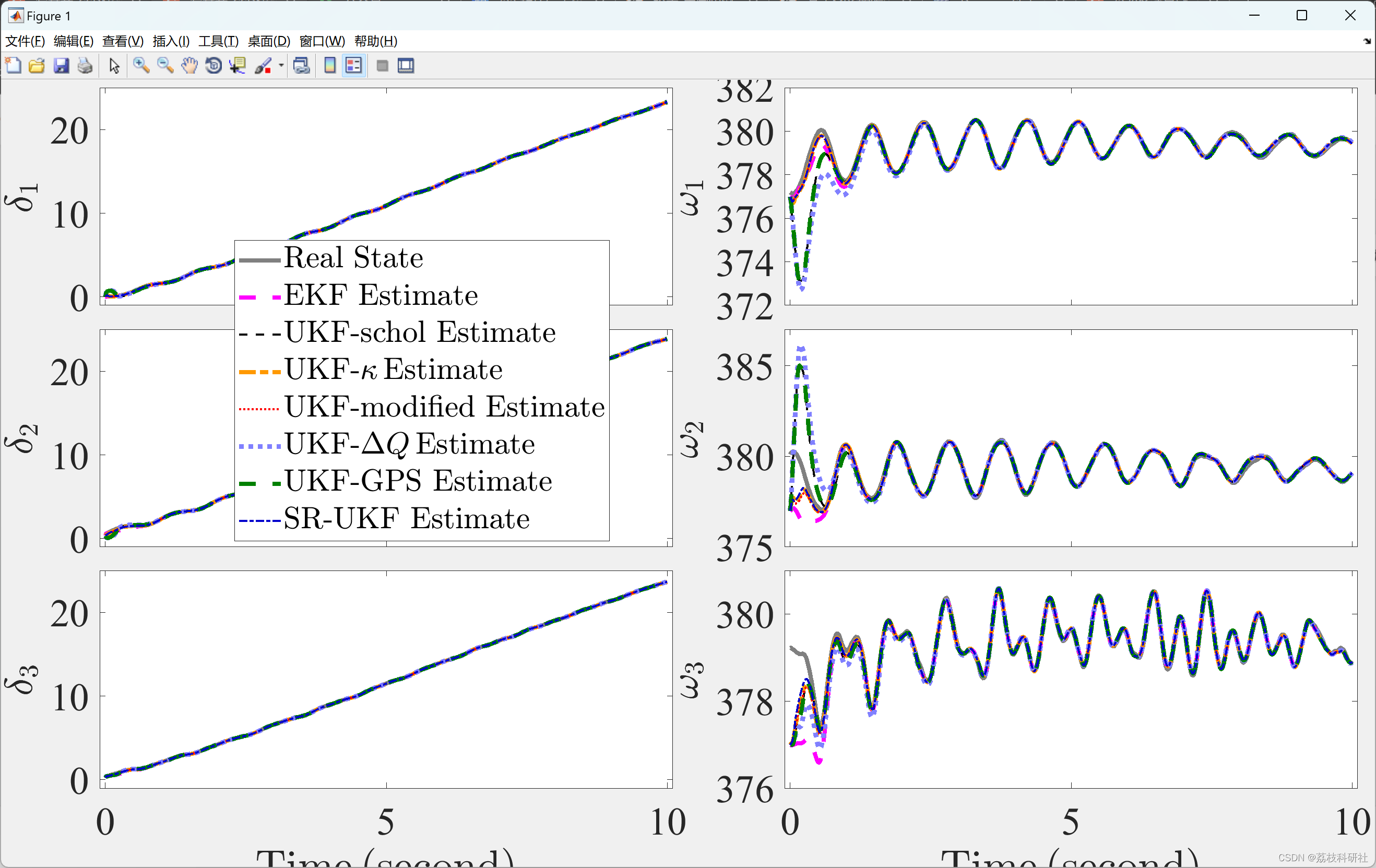
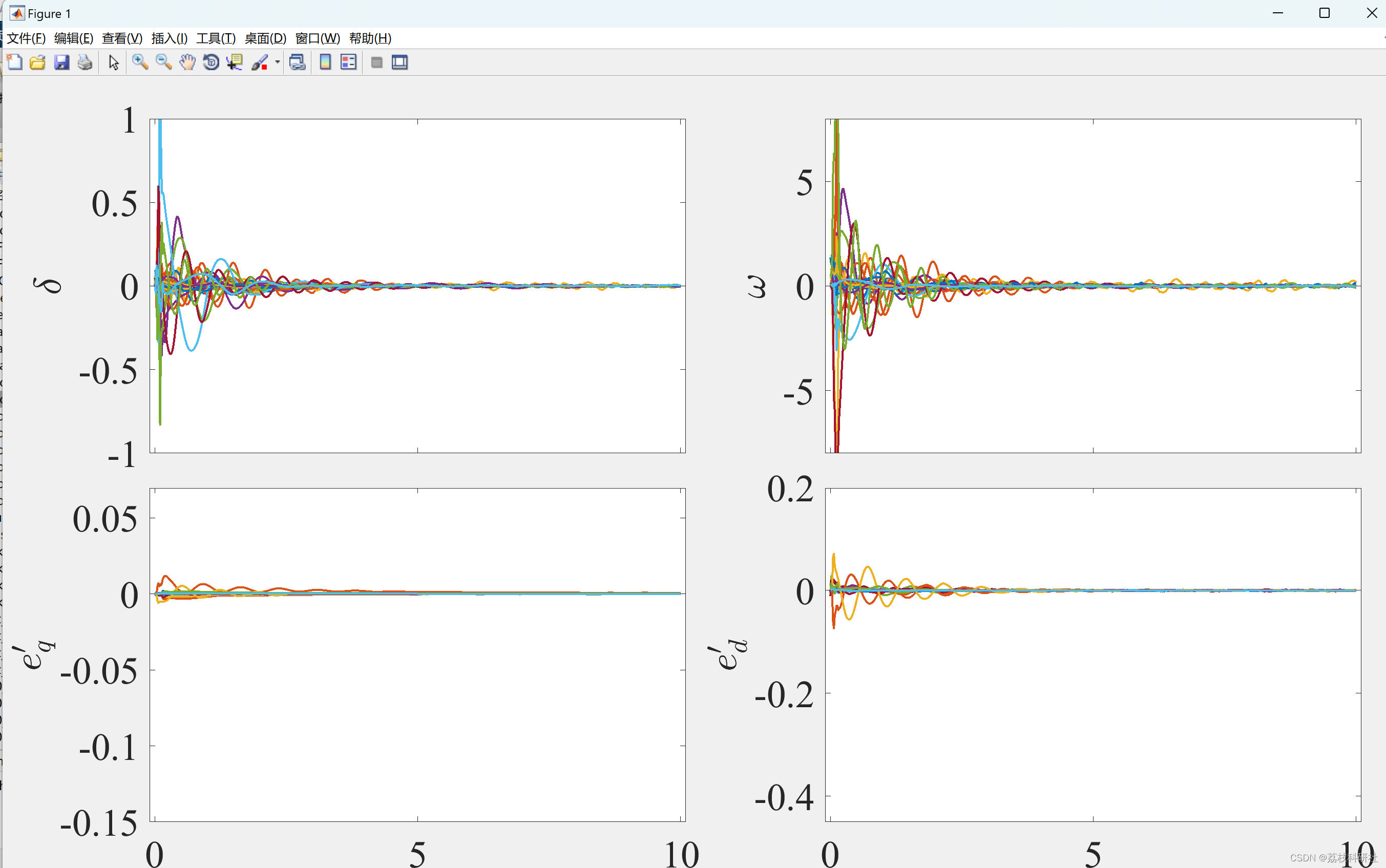
🎉3 参考文献

部分理论来源于网络，如有侵权请联系删除。

[1]J. Qi, K. Sun, J. Wang and H. Liu, "Dynamic State Estimation for Multi-Machine Power System by Unscented Kalman Filter With Enhanced Numerical Stability," in IEEE Transactions on Smart Grid, vol. 9, no. 2, pp. 1184-1196, March 2018, doi: 10.1109/TSG.2016.2580584.

🌈4 Matlab代码、数据、文章讲解