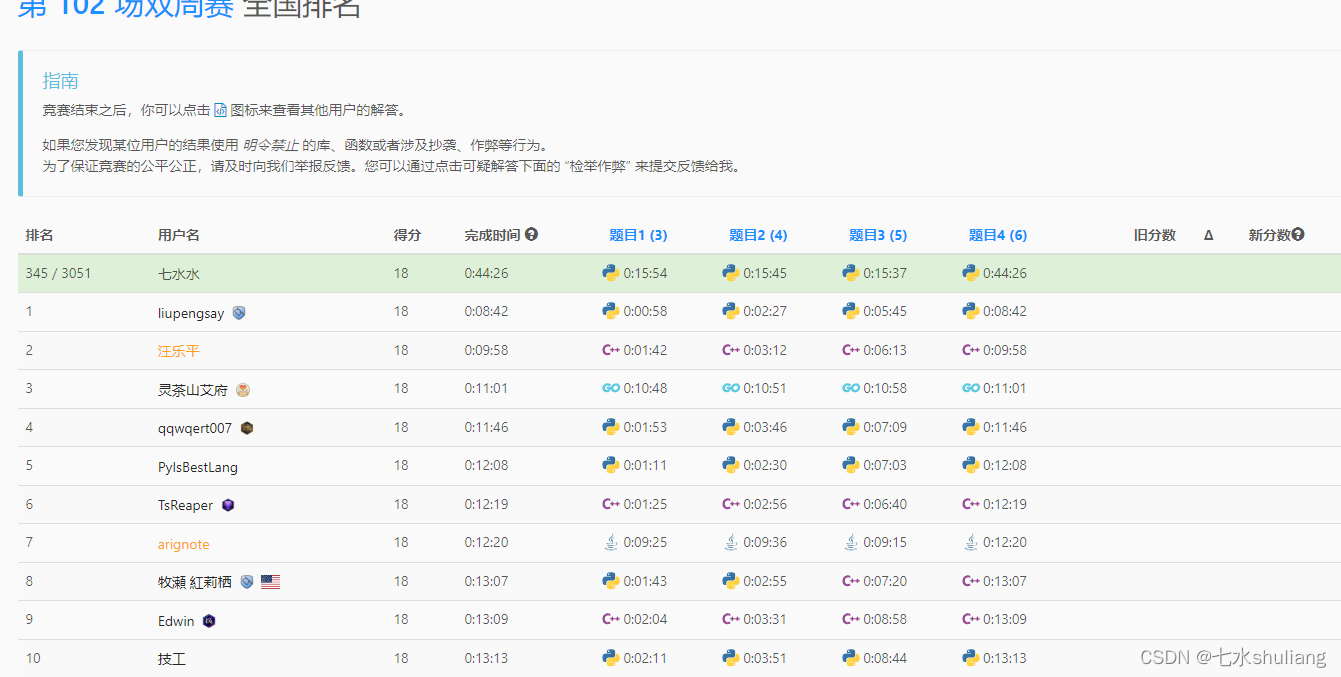
[LeetCode周赛复盘] 第 102 场双周赛20230415
- 一、本周周赛总结
- 二、 6333. 查询网格图中每一列的宽度
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 三、6334. 一个数组所有前缀的分数
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 四、6335. 二叉树的堂兄弟节点 II
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 五、6336. 设计可以求最短路径的图类
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 六、参考链接
一、本周周赛总结
- T4卡了半小时,真的不应该。
- T1 模拟。
- T2 前缀和模拟。
- T3 分层遍历。
- T4 floyd/dij(我觉得dij不是正解)。
二、 6333. 查询网格图中每一列的宽度
链接: 6333. 查询网格图中每一列的宽度
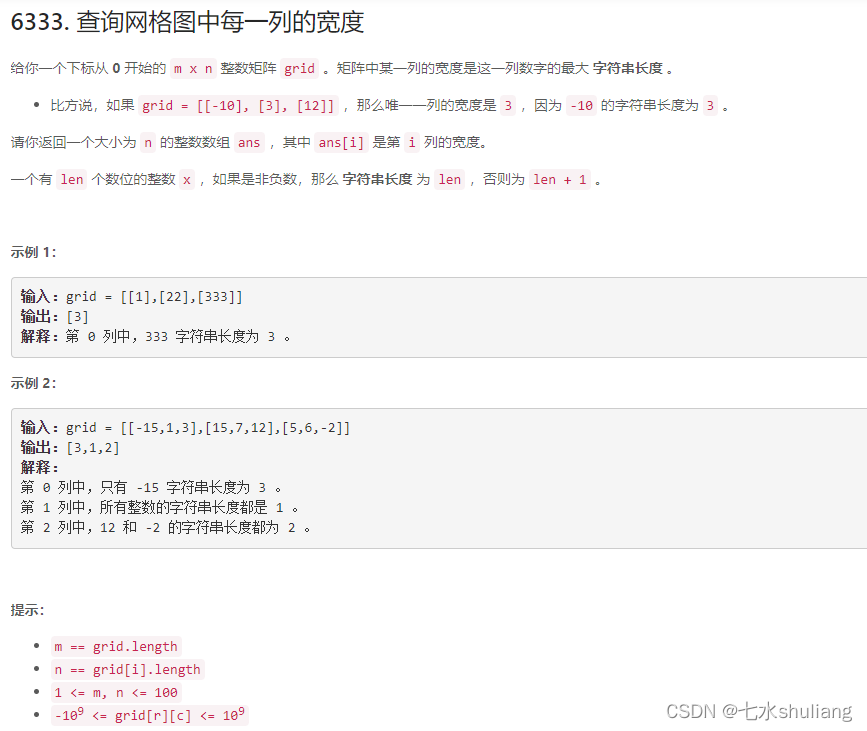
1. 题目描述
2. 思路分析
按题意模拟即可。
3. 代码实现
class Solution:
def findColumnWidth(self, grid: List[List[int]]) -> List[int]:
m,n = len(grid),len(grid[0])
ans = [1]*n
for i,row in enumerate(grid):
for j,v in enumerate(row):
ans[j] = max(ans[j],len(str(v)))
return ans
三、6334. 一个数组所有前缀的分数
链接: 6334. 一个数组所有前缀的分数
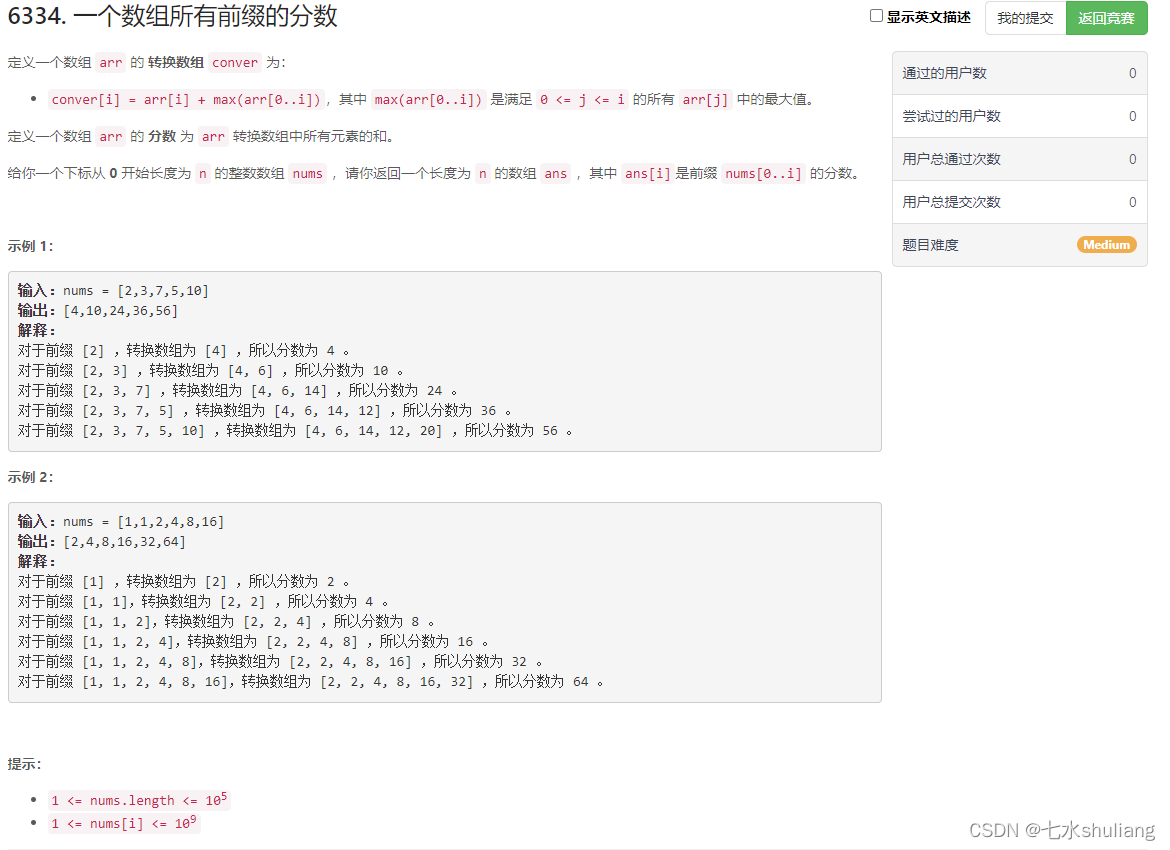
1. 题目描述
2. 思路分析
- 不要被题目的一堆变量唬住。
- 直接按题意模拟即可。
3. 代码实现
class Solution:
def findPrefixScore(self, nums: List[int]) -> List[int]:
n = len(nums)
con = [0]*n
mx = 0
for i,v in enumerate(nums):
mx = max(mx,v)
con[i] = v + mx
return list(accumulate(con))
四、6335. 二叉树的堂兄弟节点 II
链接: 6335. 二叉树的堂兄弟节点 II
1. 题目描述

2. 思路分析
- 层先法,把每层的和记下来。
- 顺便每个节点的父亲记下来。
- 那么把当前层相同父亲的值减去即可。实现时把儿子的值累积到父亲上更方便。
3. 代码实现
class Solution:
def replaceValueInTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
root.val = 0
q = [(root,root)]
fas = {}
while q:
s = 0
nq = []
sm = Counter()
for u,fa in q:
s += u.val
sm[fa] += u.val
if u.left:
fas[u.left] = u
nq.append((u.left,u))
if u.right:
fas[u.right] = u
nq.append((u.right,u))
for u,fa in q:
u.val = s - sm[fa]
q = nq
return root
五、6336. 设计可以求最短路径的图类
链接: 6336. 设计可以求最短路径的图类
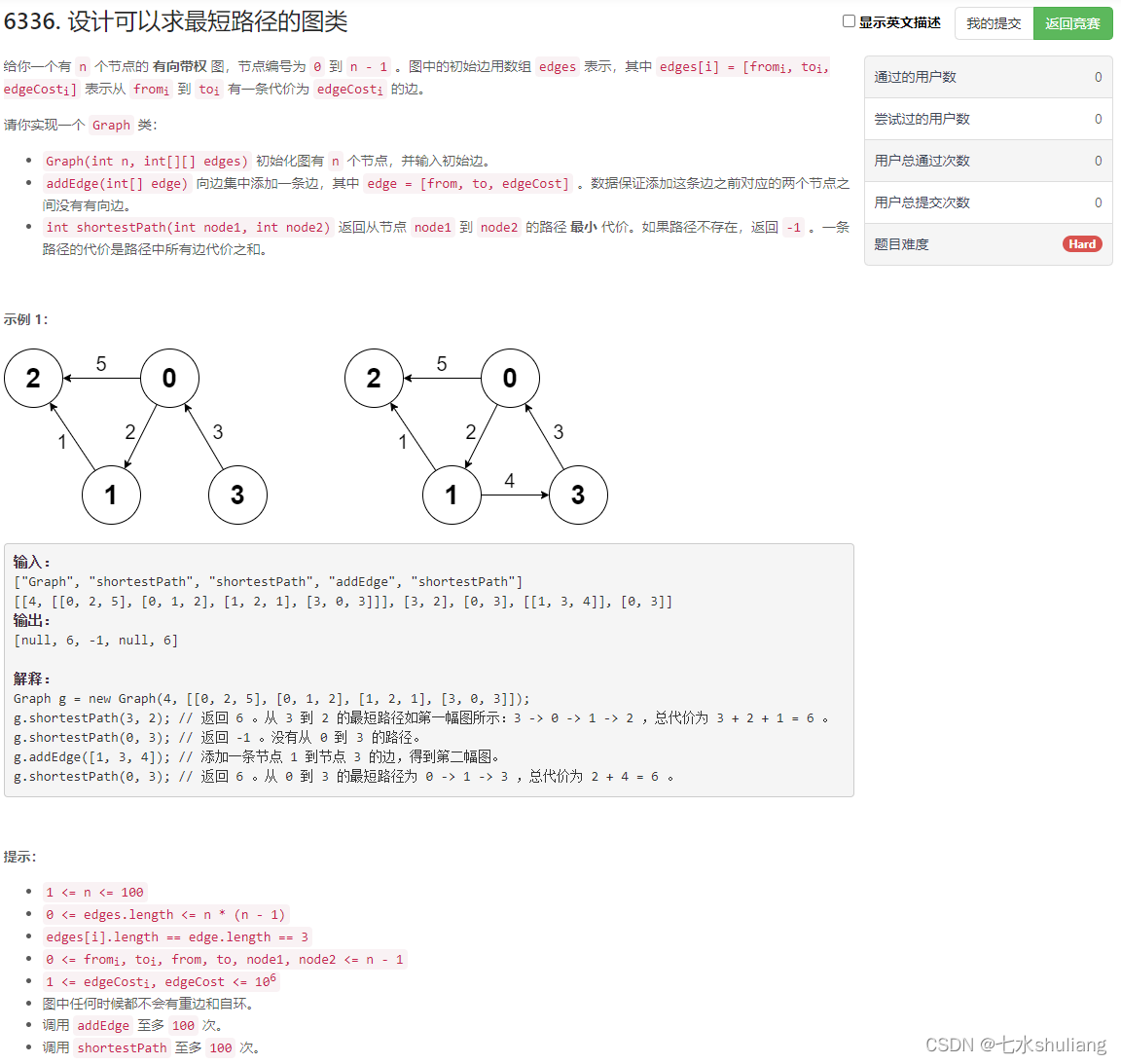
1. 题目描述
2. 思路分析
这题做得慢可惜了,acw之前考过一个逐步加点的题。这题是逐步加边。
- 用floyd,每次加边后,把两个端点作为k,做一遍floyd即可。这样查询是O(1)。
- 偷懒的做法是,前两个操作只负责建图。
- 每次查询时用dijkstra暴力算,复杂度O(nlogn + m),注意m可能比较大(n*(n-1)),最坏情况下应该慢于floyd。
3. 代码实现
floyd
class Graph:
def __init__(self, n: int, edges: List[List[int]]):
# self.g = [[] for _ in range(n)]
dist = self.dist = [[inf]*n for _ in range(n)]
for u,v,w in edges:
self.dist[u][v] = w
for k in range(n):
dist[k][k] = 0
for k in range(n): # 中间点,也就是经过的点,如果需要记path,则发现小就记k
for u in range(n): # 左短点
for v in range(n): # 右端点
dist[u][v] = min(dist[u][v],dist[u][k]+dist[k][v])
self.n = n
def addEdge(self, edge: List[int]) -> None:
n = self.n
u,v,w = edge
# self.g[u].append((v,w))
dist = self.dist
# print(dist)
if w < dist[u][v]:
dist[u][v] = w
for a in range(n):
for b in range(n):
dist[a][b] =min(dist[a][b],dist[a][u]+dist[u][b])
for a in range(n):
for b in range(n):
dist[a][b] =min(dist[a][b],dist[a][v]+dist[v][b])
def shortestPath(self, node1: int, node2: int) -> int:
d = self.dist[node1][node2]
if d == inf:
return -1
return d
dijkstra暴力
class Graph:
def __init__(self, n: int, edges: List[List[int]]):
self.g = [[] for _ in range(n)]
for u,v,w in edges:
self.g[u].append((v,w))
self.n = n
def addEdge(self, edge: List[int]) -> None:
u,v,w = edge
self.g[u].append((v,w))
def shortestPath(self, node1: int, node2: int) -> int:
n = self.n
dis = [inf]*n
dis[node1] = 0
g = self.g
q = [(0,node1)]
while q:
d,u = heappop(q)
if d > dis[u]:continue
for v,w in g[u]:
if w + d < dis[v]:
dis[v] = w + d
heappush(q,(w+d,v))
if dis[node2] == inf:
return -1
return dis[node2]