导读

EEG信号的分析过程是为了获得能够突出信号本身特定特性的值，从而对其进行表征。同时，也需要将所获得的值通过准确的绘图技术来进行正确地显示，以使这些值对用户有用且清晰易读。目前，已有许多不同的脑电信号分析和显示技术，在这里，本文将列出一些最广泛的信号分析技术和可能的显示技术。本文选择了经典的频域、时域分析，相应的参数及其主要显示技术，如大脑映射、时间趋势图和时频图。

频域EEG信号分析

频域信号分析或频谱分析是一种广泛应用于多个学科领域的技术，是磁共振成像(MRI)等许多常见过程的基础。频谱分析是基于EEG信号从时域(时间上的一系列样本)到频域(每个频率的一系列样本)的转换。这种操作的最大优点是将几秒到几小时内包含的信息压缩成几个值。根据定义，这是一种统计分析，结果将是有关EEG信号结构的平均信息，并且不会突出显示任何非常短的信号模式或任何功率较弱的信号。其基本原理是，任何信号都可以是不同振幅和相位的纯正弦分量的总和，如图1所示。

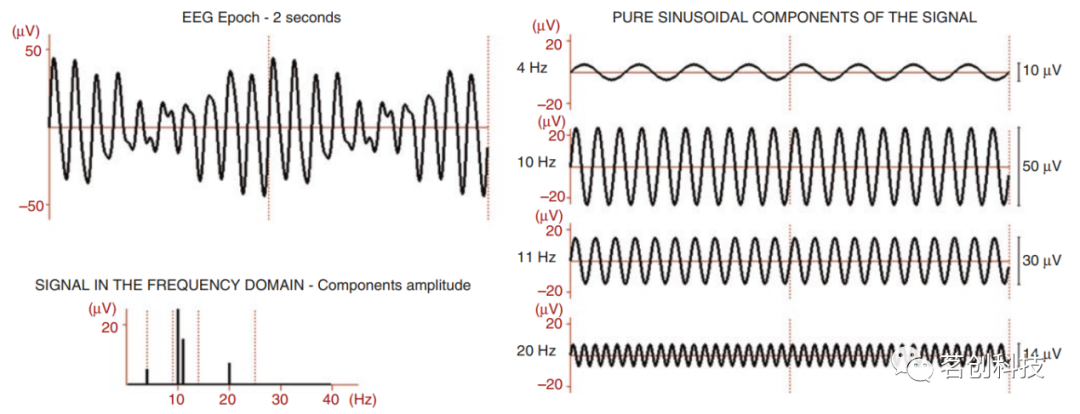
图1.将EEG信号分解为纯正弦波。

在本例中，2秒的EEG信号是4、10、11和20Hz四个分量的和，每个分量的振幅不同(4Hz分量为10μV，10Hz分量为50μV，11Hz分量为30μV，20Hz分量为14μV)。图1中的频域信号显示了每个频率的分量幅值(确切地说，是峰-峰幅值的一半)。

如图2所示，信号以频谱的形式显示，该图形显示了在频域内的每个纯正弦分量在该频率处的信号功率，称为功率谱密度(PSD)。该图形通常用连续的条形图表示，其中x轴是频率(以Hz或cycle/s为单位)，y轴是每个频率量子的功率密度(以μV2/Hz为单位)。这种分解的计算是通过离散傅里叶变换(DFT)得到的，在1970年引入的允许快速计算的版本中，其被称为快速傅里叶变换(FFT)。

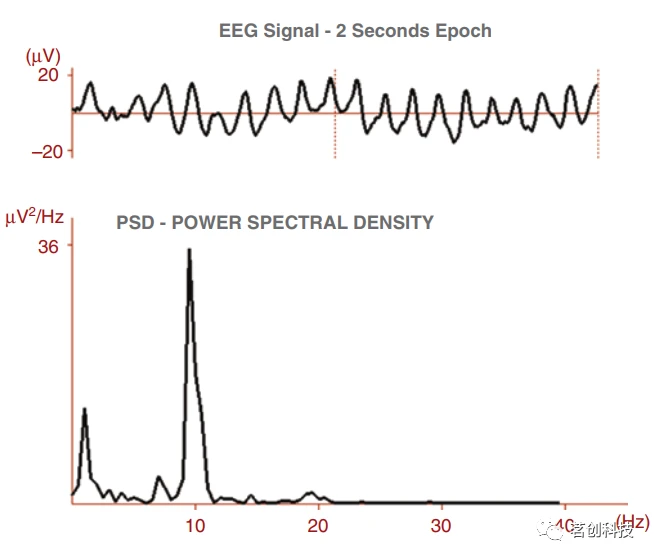
图2.以α节律为特征的EEG信号的频谱或PSD。

注意，傅里叶分析只是可能的频谱估计技术之一，其他技术如自回归模型可以参考Kay等人的文献。频谱分析是将EEG信号分割成2s或更长的时间段，然后根据傅里叶技术对每个时段进行变换以获得PSD。最后，对所有频谱执行平均并将结果进行可视化。频谱分析不是一种精确方法，而是一种平均方法，因为它突出了预定义时段内信号的谐波含量；再加上几个频谱是平均的，很明显，这种技术不能突显短信号瞬态或非常低功率的信号。为了提高频谱分析的性能，经常使用几种技术，如重叠、去趋势和渐缩。

重叠包括对重叠的epoch进行分析，即对2s的固定时段进行分析，如图3所示，从每秒开始分析。

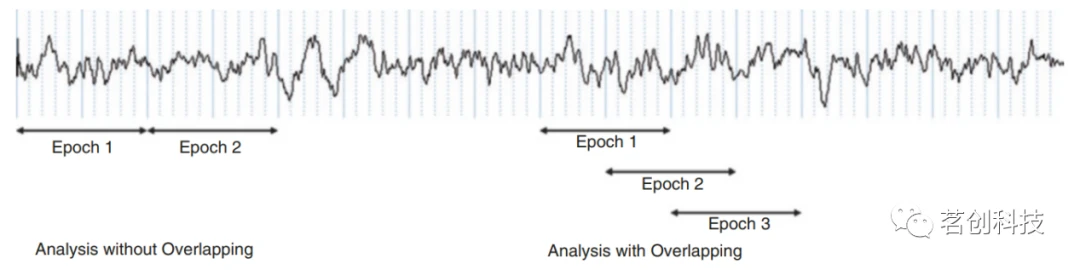
图3.有和无重叠epoch的选择示意图。

去趋势包括从每个epoch去除连续分量或斜率。从技术上讲，这意味着从EEG信号中去除最接近给定epoch信号演变的“线”，如图4所示。图4显示了对EEG信号进行最佳插值的直线，以及减去这条直线后得到的信号。由此产生的频谱以一种最能代表EEG专家在信号本身所能看到的方式突出了功率的改变。被移除的信号的“慢”分量很少用于分析，而快速分量则被突出显示，因为它们通常对分析来说是最重要的。

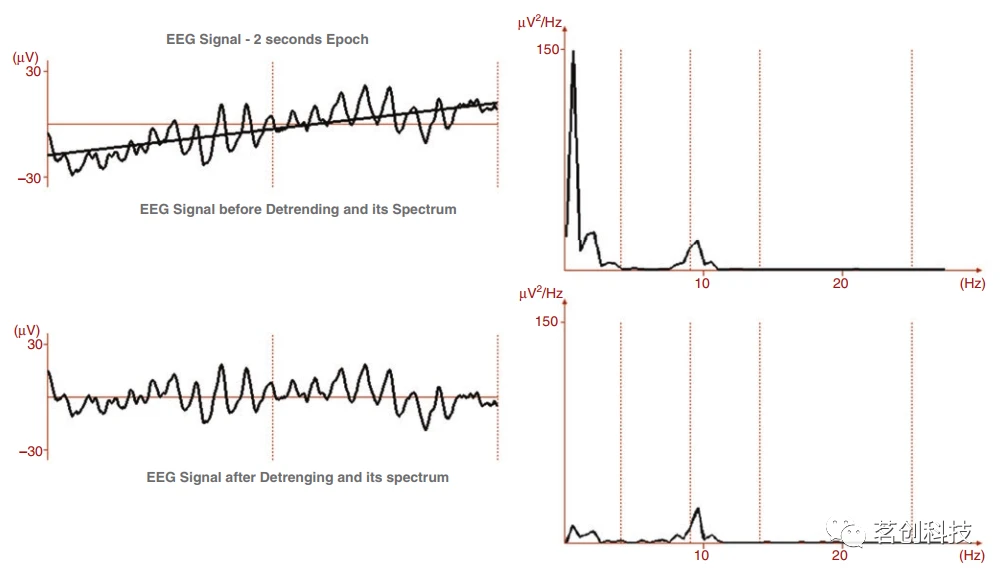
图4.EEG信号时段去趋势的例子。

信号的渐缩或加窗，旨在减少频谱泄漏现象，即在频谱中传播信号的功率，往往会隐藏信号中可能具有较弱功率的重要分量。这项技术所获得的改进非常重要，特别是在高功率的主导信号(即慢脑电图波)可能“掩盖”其他重要成分(即α节律)的情况下。从技术上讲，这个操作包括将任何信号epoch乘以一个给定的函数，该函数在epoch的极值处通常等于0。

频域EEG参数

一旦对EEG信号进行了标准的频谱分析，将其适当地划分为多个epoch，并使用上一段中描述的技术，就可以得到所分析EEG信号的平均频谱。然后，将该频谱分成通常用于描述EEG节律的部分，即delta、theta、alpha和beta，如图5所示。

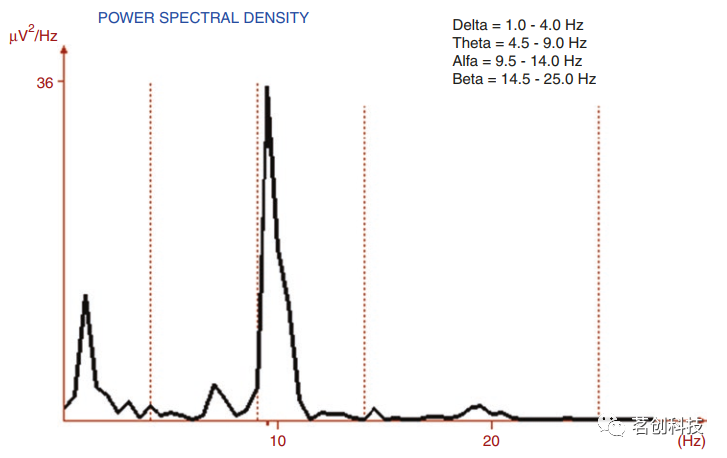
图5.将EEG信号的PSD分成标准频段。

通过这种方式划分频谱，可以计算其他几个数据，这些数据可以总结出EEG信号的有趣特征，这些特征可以量化通常由目视检查确定的内容，如下所示：

①不同频段的绝对功率。这些值被计算为每个频段的频率区间内信号频谱下的面积，如图6所示。其测量单位是μV2。

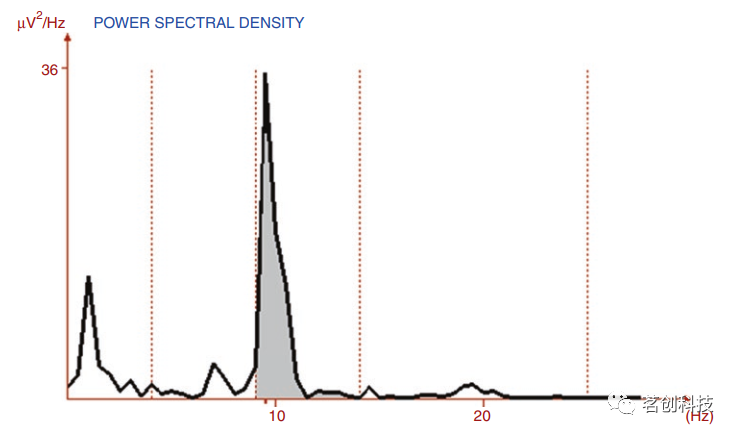
图6.alpha频段的绝对功率用频谱下的面积(阴影区域)表示。

②不同频段的相对功率。这些值可以根据一个频段的绝对功率与总功率(即所有频段的功率之和)之间的比率来计算。假设使用四个标准频段，可以得到：

③作为两个同源值之间的比率，结果通常用百分比表示。

④PPF-峰值功率频率。即频谱的峰值所在的频率，如图7所示。这种计算可以限制在每个频段所定义的频率区间内。测量单位为频率，即Hz或cycle/s。

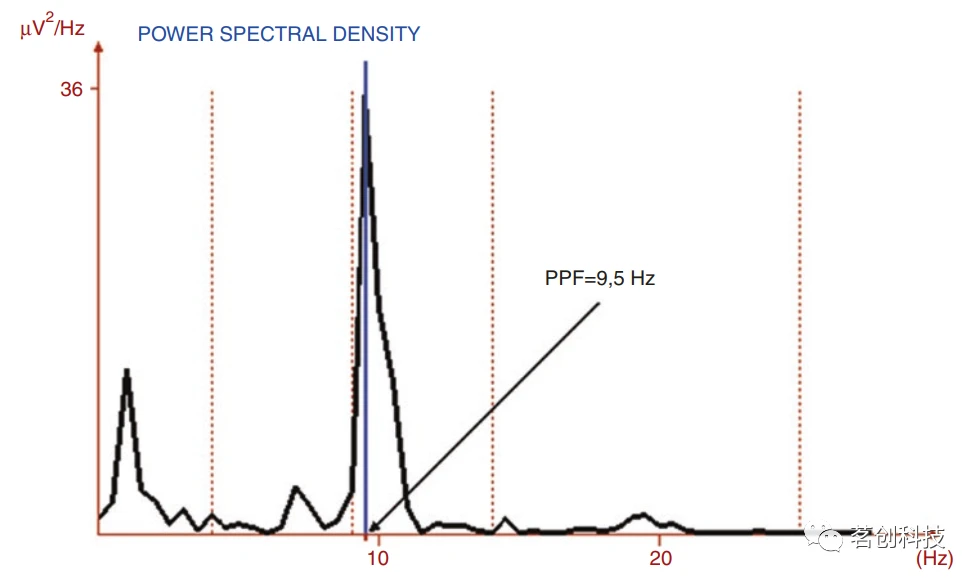
图7.在EEG信号频谱上计算PPF的实例。

⑤MF-中值频率。这是将频谱分成两个区域的频率，每个区域占总功率的50%，如图8所示。测量单位为频率，即Hz或cycle/s。

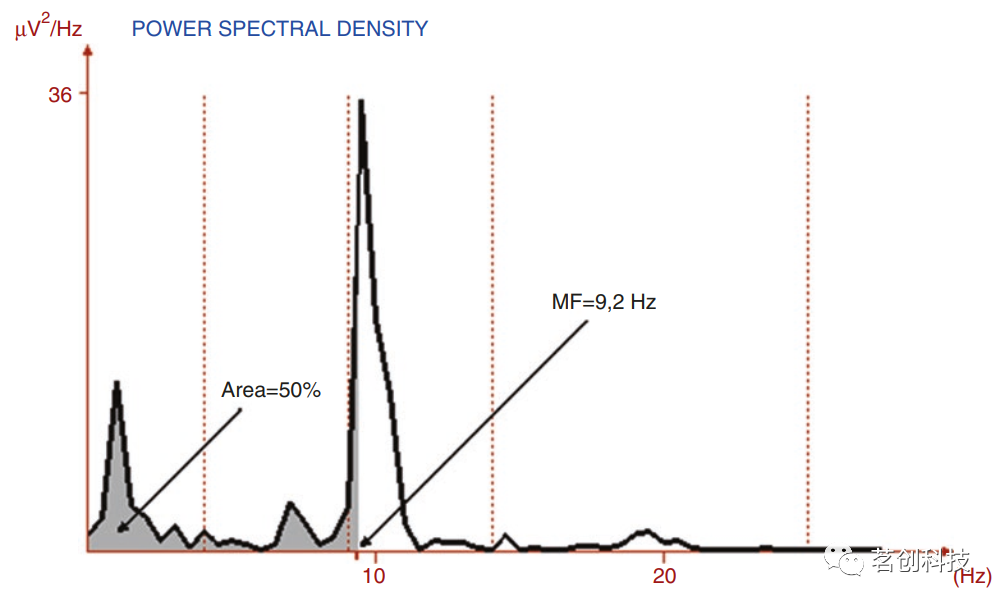
图8.在EEG信号频谱上计算MF的实例。

⑥SEF-频谱边缘频率(或称边缘频率)。也就是指频谱的“大小”。它可以通过不同的方法获得，通常被定义为占总功率95%的频谱区间，如图9所示。测量单位为频率，即Hz或cycle/s。

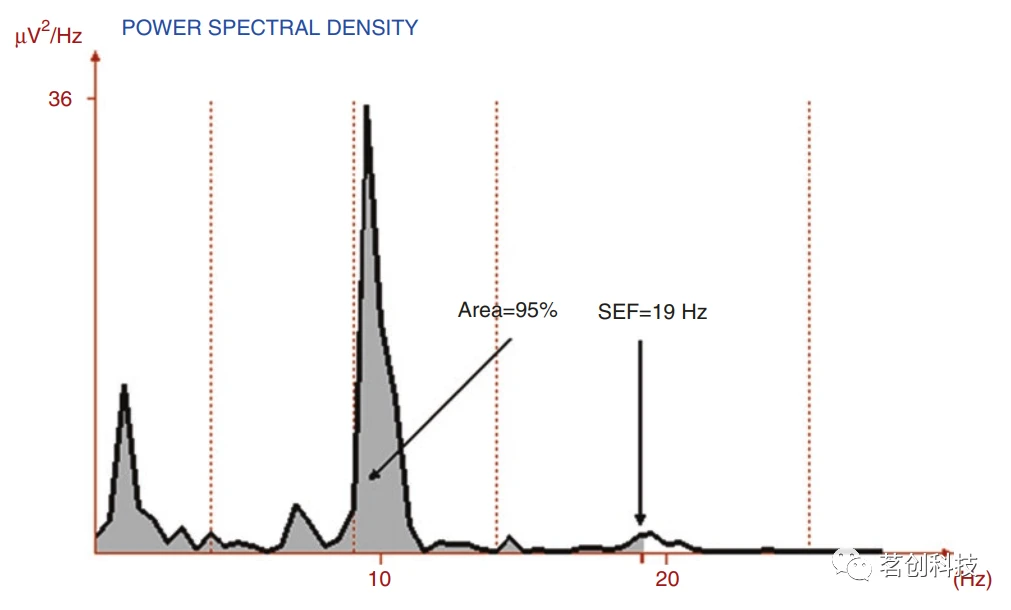
图9.在EEG信号频谱上计算SEF的实例。

⑦MDF-主频。这是频谱的主频率，定义为每个频率上的功率加权后的频率均值，计算公式如下。测量单位为频率，即Hz或cycle/s。

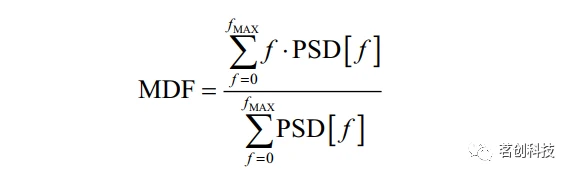
所有这些参数都可以单独使用或组合使用来定义新的变量，通常称为指标。文献中一个常见的例子是theta/alpha的商，它被计算为相同信号的theta频段的绝对功率与alpha频段的绝对功率之间的比率。很容易理解，其他几个指标既可以定义为同一信号参数的函数，也可以定义为不同信号参数的函数。后者的一个例子可以是大脑不同侧的两个电极的相同参数之间的比率，从而定义了一种不对称指数。

这些指标通常是同源对象之间的比率，具有一定的优势：

①它们可以以一种非常简洁的方式表示信号的复杂特征。

②一般来说，它们对伪影不太敏感。

③通常对不同被试信号绝对功率的巨大差异不太敏感，这是它们与相对功率共有的特征。

时域EEG信号分析

在时域中计算的EEG参数都是直接对原始信号进行的测量或计算，而不像在频谱分析中那样进行任何转换。

时域EEG参数

时域的EEG参数有多种，这里将阐述那些在文献中经常使用和引用的参数：

①过零：定义为EEG信号穿过基线的次数，如图10所示。但是，这个参数并不总是代表EEG中所谓的信号节律。通常情况下，感兴趣的节律嵌入到慢波中，这会使得计算出现错误。

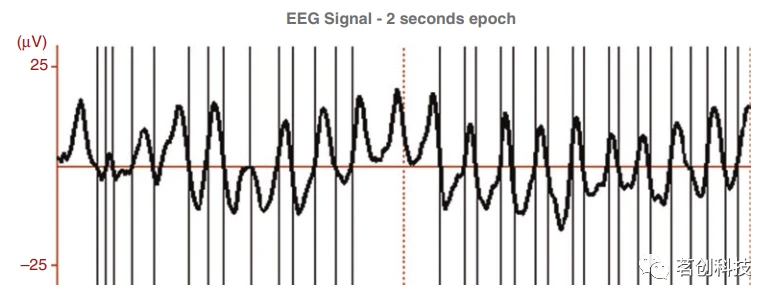
图10.EEG信号“过零”计算示例。

注意，在该例子中，2秒内有32次过零点，即每秒16次，这可能会导致信号节律为8Hz，但实际上约为10Hz。问题在于信号在一定间隔内的漂移，使其避免越过基线而丢失了一些过零点。

②突发抑制率(BSR)：这是一个量化EEG信号抑制程度的参数。它是在固定持续时间epoch上进行计算的，即信号在给定阈值(±5μV)以下保持稳定的时间与epoch持续时间的比率，如图11所示。为了考虑EEG信号是否被抑制，信号至少在400-500ms内不必超过阈值。如果在一个epoch内存在多个抑制间隔，则应该将它们相加。实际上，该参数设置了被抑制信号在epoch中所占的百分比。

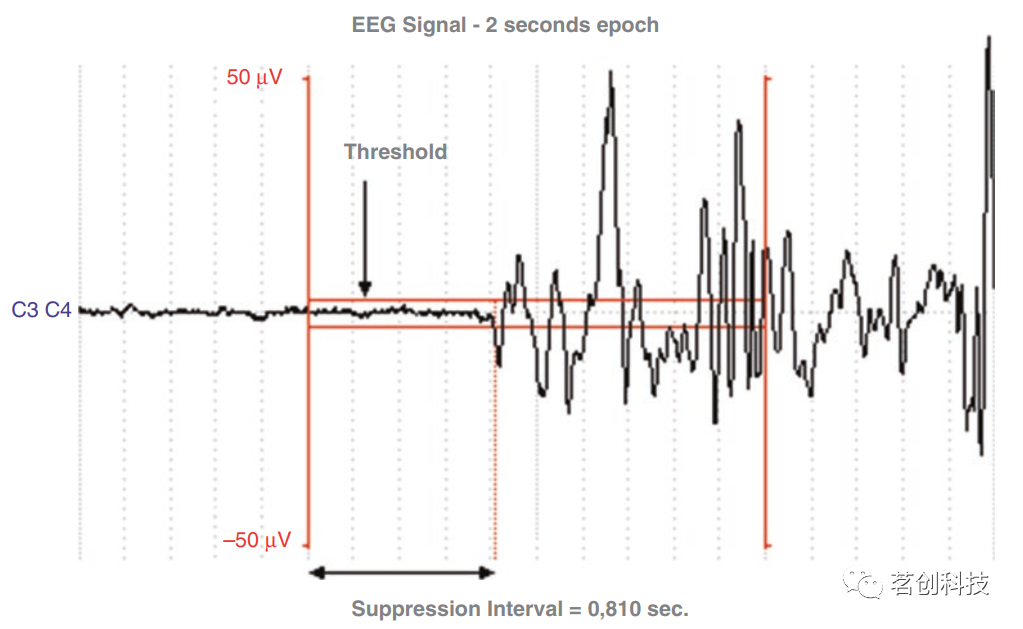
图11.计算EEG信号的“突发抑制率(BSR)”。

在此示例中，在2s的epoch上有一个0.810s的抑制间隔，则BSR为0.810/2.000=0.405，即40.5%。

数据显示技术

数据显示是任何类型分析的基础。在选择显示技术时，重点关注应该突出哪些特征：A.数据随时间的演变；B.数据的空间分布。接下来，将根据这两种选择来分析最广泛使用的显示技术。

①直方图和趋势。这些是显示参数随时间变化的更简单(通常也是最有效)的技术，但其缺点是不允许在同一图形上显示许多变量，以避免易读性受到影响。时间通常用水平轴表示，在另一个轴上显示参数。这个图形可以显示任何类型的参数，这些参数在时域和频域中计算。图12中的例子显示了在颈动脉内膜切除术期间记录的EEG，在右半球(浅灰色)和左半球(深灰色)的所有推导上计算出两个绝对功率的趋势。

图12.左右半球绝对功率的趋势。

②压缩谱阵列(CSA)。这是过去常用于频谱分析的一种显示类型，其在显示功率谱随时间的变化方面提供了优势。它包括随时间推移获得的功率谱的垂直连续显示，如图13所示，然后得到一个具有前景效应的图形。

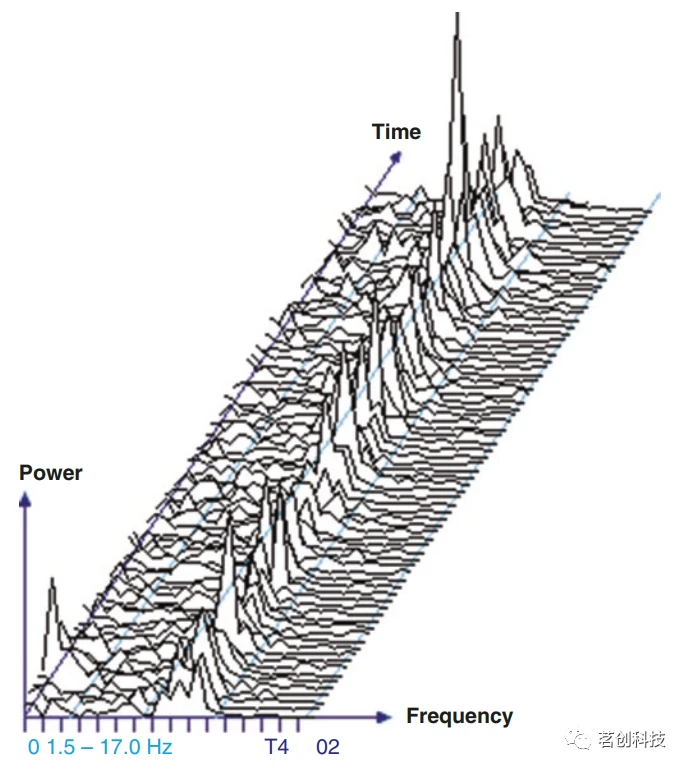
图13.以α节律为特征的EEG压缩谱阵列(CSA)。

x轴表示频率，y轴表示功率，每个频谱之间的步长表示每个间隔之间的时间，所以z轴表示时间。这种显示方法可以很容易地显示背景节律随时间的变化。它仍然需要由专家来解释，并且存在一定的问题，因为大型伪影可以很容易地隐藏在最后绘制的频谱后面。这就是这种技术被DSA取代的原因。

③密度谱阵列(DSA)。这是显示频谱分析时间演变的另一种技术，它使用色标来显示频谱中每个频率量子的功率。这意味着每个功率谱都由一个彩色条纹(或灰度条纹)表示，其中y轴代表点的频率；点的颜色表示该频率处频谱的功率。这些条纹的顺序代表了频谱的时间演变，即DSA，如图14所示。

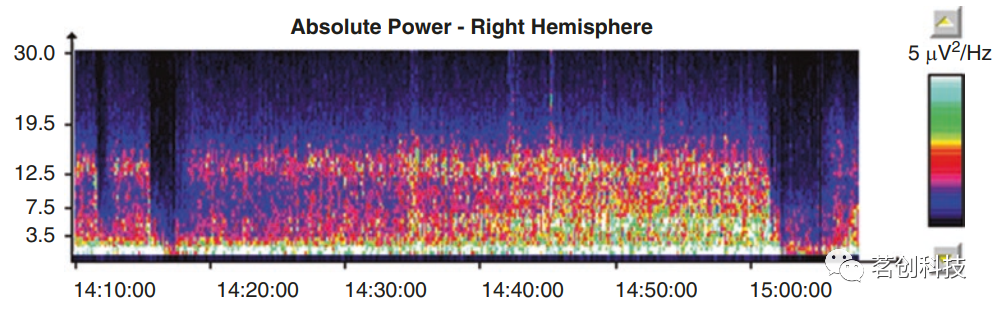
图14.密度谱阵列。

④小波。这是一种与DSA非常相似的技术，DSA是一种使用色度来显示给定时间内每个频率分量功率的时频图。与DSA的区别在于所使用的频谱分析技术，不是简单的傅立叶变换，而是更复杂的小波变换，它可以更好地显示频率分量的功率，即使是在最短的时间间隔内，以毫秒为单位。这样可以进行更详细的数据分析，但同时也失去了全局概览特性，而这正是DSA的优势之一。因此，小波变换被用于分析短时间间隔，如诱发电位或如图15所示的特定EEG模式(即尖峰)，但原则上可以用于较长的EEG间隔。

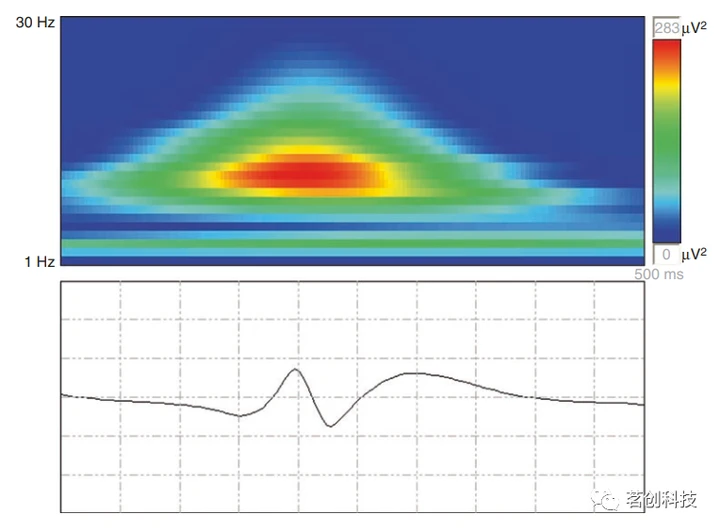
图15.尖峰波信号的小波变换。

⑤aEEG-振幅整合EEG。这是一种对EEG进行时域显示的技术，该技术执行特殊的数据处理，可以总结如下：

A.执行2-15Hz之间的选择性带通滤波

B.信号在半对数尺度上进行变换

C.信号整流

D.平滑以仅识别结果信号的最大和最小峰值

E.结果图形

使用该技术得到的图形显示了信号幅值的压缩信息，主要显示了最大峰和最小峰的振幅，如图16所示。

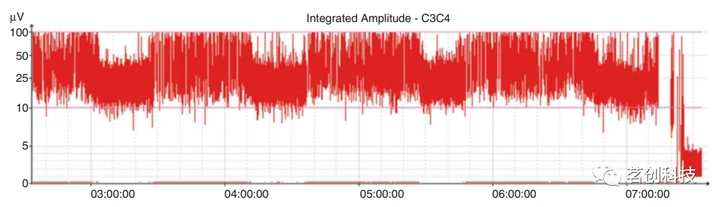
图16.aEEG轨迹。

显示数据的空间分布

大脑映射是一种旨在显示活动在头皮上的空间分布的技术，而这种活动仅在头皮上的几个点上进行测量。一旦从这些点的值计算出这种分布，就可以获得所谓的映射。根据活动的类型，可以得到以下结果：

①振幅图：这是在给定时间测量到的EEG信号振幅在头皮上的分布。

②频率图：这是在进行频谱分析的一个或多个选定时间间隔内，计算出EEG信号在给定频段内的平均功率在头皮上的分布显示。

③相干图：这是在进行频谱分析的一个或多个选定时间间隔内，计算出EEG信号在给定频段内的平均相干性在头皮上的分布显示。

接下来将概述执行正确大脑映射的基本要素，通常指的是要映射的一般实体(振幅、功率或其他)。

（1）空间采样

大脑映射是基于空间采样原理。在这种情况下，对空间采样的深入分析可能过于复杂；唯一重要的是要指出以下原则：在不同的空间方向上，与测量数量(测量点是电极)相比，信号不应该有过高的变化。如图17的例子所示，如果在10cm的空间内使用10个电极，然后得到10个测量值(FSAMP=100个sample/m)，则信号不能超过每米50个“波”(50=最大空间频率，即FSAMP/2)，也就是说，在10cm的空间内，被测信号最多可以有5个“波”。假设空间采样均匀，则应该在空间的所有可能方向上进行验证。

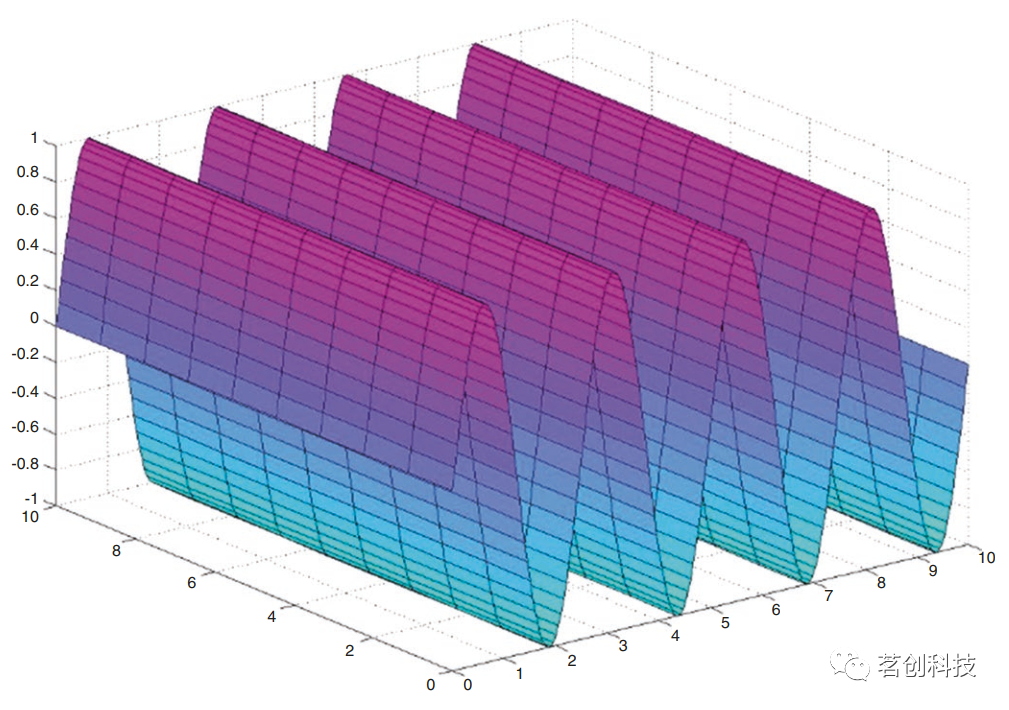
图17.沿x轴有4个“波”的信号。

考虑到不可能限制信号具有一定的空间变化，人们可以简单地调整头皮上测量点的数量，以适当地覆盖待检测信号的所有可能的空间变化。

为了正确地识别EEG信号的空间变化量，即活动如何在不同的点之间变化，几项实验得到的结果如下：

①为了在标准临床应用中正确映射大脑EEG活动，使用的最少电极数量为25个，其位置基于颅脑解剖标志的20%和10%的标准化测量。这25个电极(以前是19个)，分别是Fp1、Fp2、F9、F7、F3、Fz、F4、F8、F10、T9、T7(ex T3)、C3、Cz、C4、T8(ex T4)、T10、P9、P7(ex T5)、P3、Pz、P4、P8(ex T6)、P10、O1和O2，如图18所示。

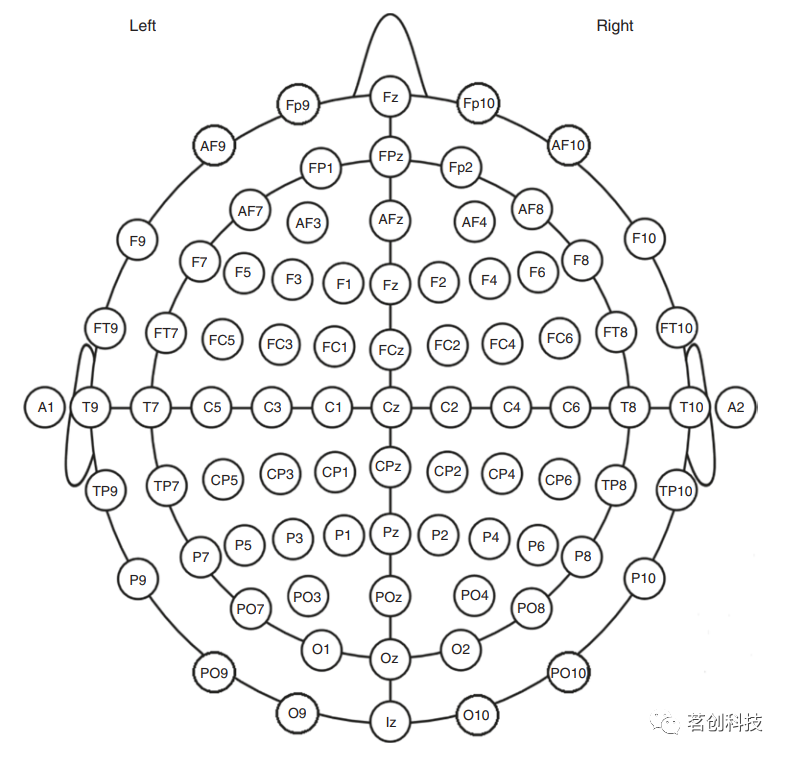
图18.IFCN标准10/10电极系统名称及标准位置。

②对于需要像源定位那样进行精确空间定位的大脑EEG活动的正确映射，至少需要64个电极，根据图18中的方案进行定位。这种记录通常使用64~256个电极，被称为高密度脑电图(HD-EEG)，目前广泛应用于临床。

（2）头皮模型

为了实现正确的大脑映射，需要定义一个正确的头皮模型。定义头皮模型后，就需要使用模型的相同坐标系来测量(或定义)电极位置。头皮模型基本上可以分为三类：

①平面模型：这些是在平面上定义的模型，其中轮廓可以是圆周或类似于头部或大脑的轮廓。由于这些模型比较简单，现在仍然被广泛使用。坐标系为直角坐标系，即每个电极的位置由坐标(x，y)表示，其坐标值通过被测(或假设)电极位置在轴向平面上的投影来获得。

②三维球形模型：这些是更精细的模型，因为该模型是在接近头皮的半球上放置电极。这些模型已被广泛应用于研究中，其有效性已被证明优于平面模型。在这种情况下，坐标系统可以由坐标(x，y，z)表示，对于每个电极，只需指定两个坐标，称为纬度和经度。通常，纬度在Cz处为0，经度在T8处为0，如图19所示。

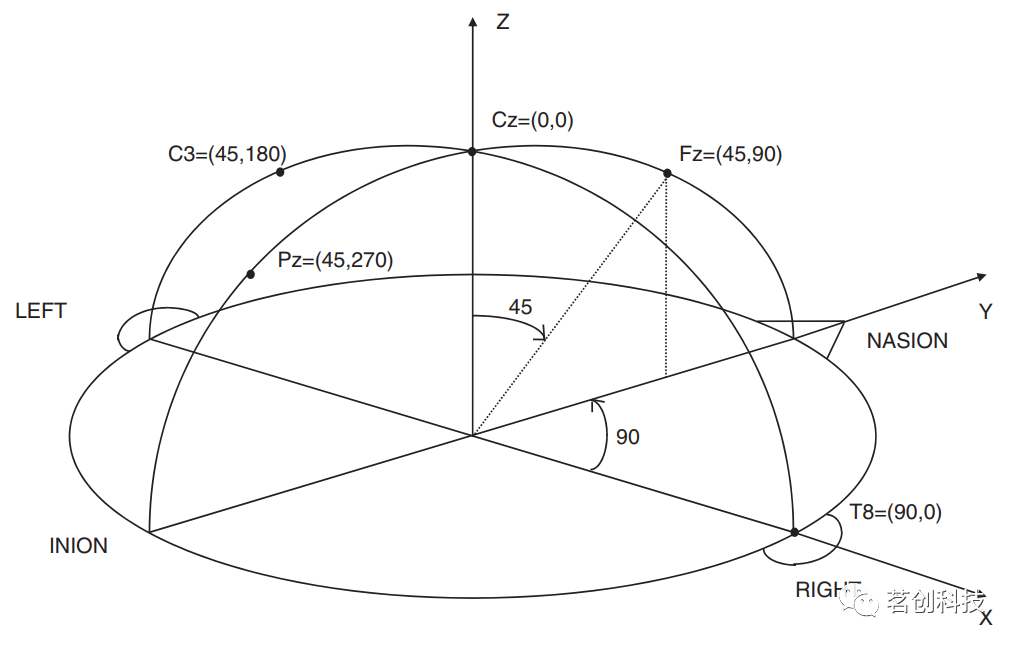
图19.三维球面模型的坐标系。

③逼真的三维模型：这些模型试图通过处理被试的MRI数据来获得头皮表面的模型。为了做到这一点，需要专门的软件来读取MRI数据，然后对这些数据进行处理，得到由体素组成的头部三维模型，然后创建模型。图20所示是这种三维模型的示例和头皮近似。

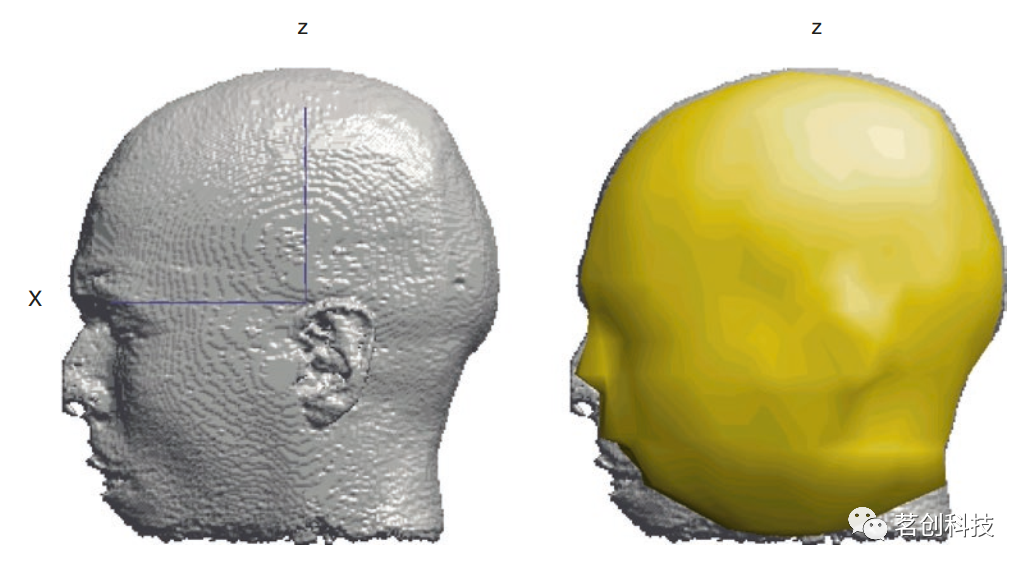
图20.通过MRI获得的三维头部模型(左)和头皮模型(右黄色)。

（3）插值技术

下面将分析三种常用的算法：

①K-NN插值：K-NN法，即K-最近邻，通过距离该点本身最近的K个电极上的测量值来插值给定点上的信号值。一般情况下，该点的值可以用K个最近的电极值的加权平均值来计算，其中权重与点到电极的距离成正比。这是一种非常简单和快速的技术，包括在头皮上放置电极，这是过去最常用的大脑映射技术。这是一种所谓的“局部”方法，意味着对于某一点的信号值的估计，在该点的邻近范围内使用有限数量的已知测量值。这种插值技术可以用于前面讨论的任何头皮模型。

②基于平面样条的插值：这种技术是一种“全局”技术而不是“局部”技术，因为所有测量电极的值都用于计算头皮模型中给定点的插值信号。从数学上讲，这是一个非常复杂的过程，其结果是通过最小化平面的曲线得到的，该平面必须通过所有已知点，这些点可以放置在头皮上的任何位置。得到的连续曲面是规则的，其最大值和最小值不一定位于电极的位置。这种插值技术可以用于前面讨论的任何头皮模型。

③基于球面样条的插值：该技术在特性和性质上与前一种技术非常相似，通过最小化流经所有已知点的球面曲线来获得插值信号的值。这也是一种“全局”插值技术，可以得到连续且规则的表面，允许将电极放置在头皮上的任何位置，但只能与三维模型结合使用。

（4）大脑映射参考点的选择

由于大脑映射旨在显示头皮上所有点的信号值，因此该信号应在绝对意义上进行测量。这些测量值都被称为“共同电极”，具有两个基本特征：

①位于中性点的共同电极：在这种假设中(可以通过将双侧耳垂连接到记录系统的共同参考来近似)，电位可以在记录时使用，而无需预先处理，因为它们应该已经确定了每个电极的绝对值。

②位于激活点的共同电极：在这种假设中(通常情况下，放大器的共同参考连接到位于头皮激活点的电极上)，需要对电位进行处理，以便从中减去共同电极的活动。在这种情况下，通常使用平均参考和源参考。

参考文献（上下滑动查看）：

Cooley JW, Tukey JW. An algorithm for the machine calculation of complex Fourier series. Math Comput. 1965;19:297-301.

Kay SM, Marple SL. Spectrum analysis—a modern perspective. Proc IEEE. 1981;69(11):1380-419.

Rampil IJ. Electroencephalography. New York: Raven Press; 1994.

Maynard DE, Prior PF, Scott DF. Device for continuous monitoring of cerebral activity in resuscitated patients. Br Med J. 1969;4:545-6.

Seeck M, et al. The standardized EEG electrode array of the IFCN. Clin Neurophysiol. 2017;128:2080-77.

Nuwer MR, Comi G, Emerson R, Fuglsang-Frederiksen A, Guérit JM, Hinrichs H, Ikeda A, Luccas FJ, Rappelsburger P. IFCN standards for digital recording of clinical EEG. International Federation of Clinical Neurophysiology. Electroencephalogr Clin Neurophysiol. 1998;106:259-61.

Wahba SG. Spline interpolation and smoothing on the sphere. SIAM J Sci Stat Comput. 1981;2:5-16.