实验一主要实现简单的刚体动画模拟(一只兔子)，包括 impulse 的碰撞检测与响应，以及 Shape Matching方法。

完整项目已上传至github。

---

简单刚体模拟(不考虑碰撞)

物体在场景中的位置由其平移矩阵，以及旋转矩阵决定（刚体不能形变，所以不需要缩放矩阵）。

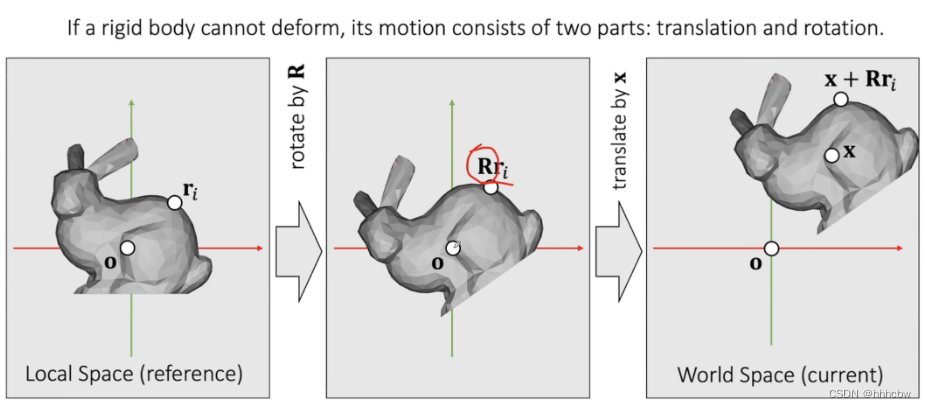
平移运动

对于平移运动，状态变量(state variable) 包括位置 x 和 速度 v，其正常更新如下

但这个积分没法在计算机内直接求，可以使用数值积分的方法进行运算，比如显式积分和隐式积分

• 显式积分
• 隐式积分
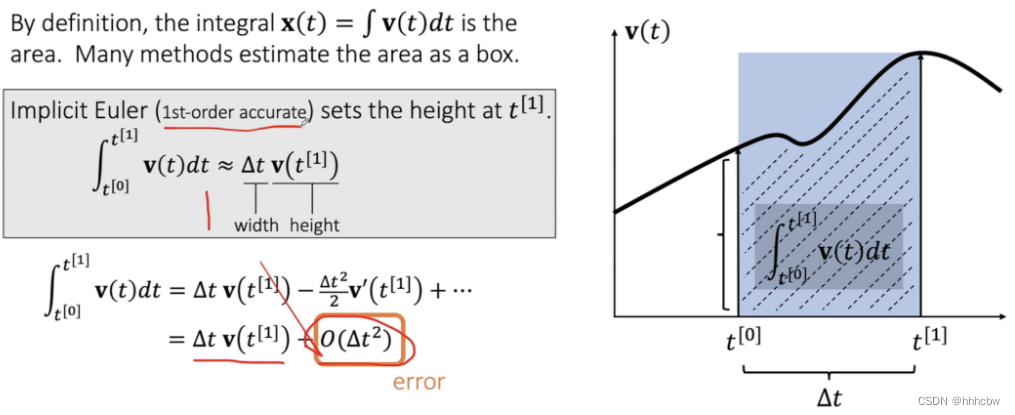  这里我们采用 Leapfrog Integration 方法，其在速度的更新上采用显式积分，而在位置的更新上采用隐式积分。
  
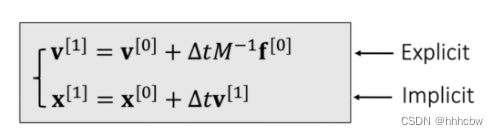
  那么在仿真过程，平移运动的更新过程如下，这里的 $△t$ 为用户指定的变量。
  
  在 lab1 中的对应代码如下，这里只考虑了重力，linear_decay 表示速度的衰减系数，比如空气阻力等。

// Part I: Update velocities
v += dt * gravity;
v *= linear_decay;

//Update linear status
Vector3 x = x_0 + dt * v;

旋转运动

旋转运动在仿真中一般使用矩阵、欧拉角以及四元数表示，对于矩阵与欧拉角都有一定的缺点，这里主要使用四元数(当然它们能互相转换)。

我们选择四元数 q 表示朝向，即从局部坐标转化为全局坐标。再使用一个3D向量 $\vec{\omega }$ 表示角速度(angular velocity)。

• $\vec{\omega }$ 的方向为旋转轴的方向
• $\vec{\omega }$ 的大小为角速度的大小

这里引入力矩，其表示如下。与力的作用会改变平移速度相同，力矩会改变角速度。

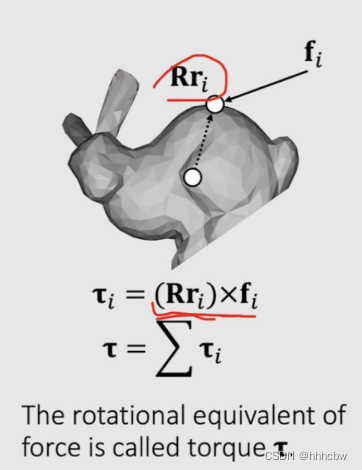
我们知道动量表示为 $\vec{P}=m\vec{v}$，而角动量表示为 $\vec{L}=I\times \vec{\omega }$ 这里的 $I$ 为一个3x3的矩阵，称为惯性张量，其描述了物体中的相对于质心的的质量分布，其可以如下表示。我们把刚体看作很多粒子(质点)组成的质点系，这里的 $r_i$ 表示该粒子(质点)在局部系中的位置，$m_i$ 表示该质点的质量，$R$ 表示旋转矩阵，即将局部系转为全局系的矩阵，其可以由四元数q转换得到。这里先求出一个 $I_{ref}$ 的目的是其可以在仿真开始前就计算出来，仿真过程中只需要计算 $I=R{I}_{ref}{R}^T$ 即可，减小计算开销。

与 $\vec{P}$ 的微分表示力类似，$\vec{L}$ 的微分表示力矩$\tau$。且 $\vec{L}$ 的微分也可表示为 $I\times \vec{\beta }$ 的形式，这里的 $\vec{\beta }$ 表示角加速度。那么仿真过程中角速度的更新如下

由于lab1中只考虑了重力，所以其力矩和角速度是不需要更新的，当然碰撞之后对于的角速度要更新。

---

粒子碰撞检测与响应

碰撞检测

我们可以使用 $\varphi (\vec{x})$ 定义位于$\vec{x}$位置的粒子到一个曲面的有向距离，其符号由粒子位于曲面的内侧还是外侧确定。

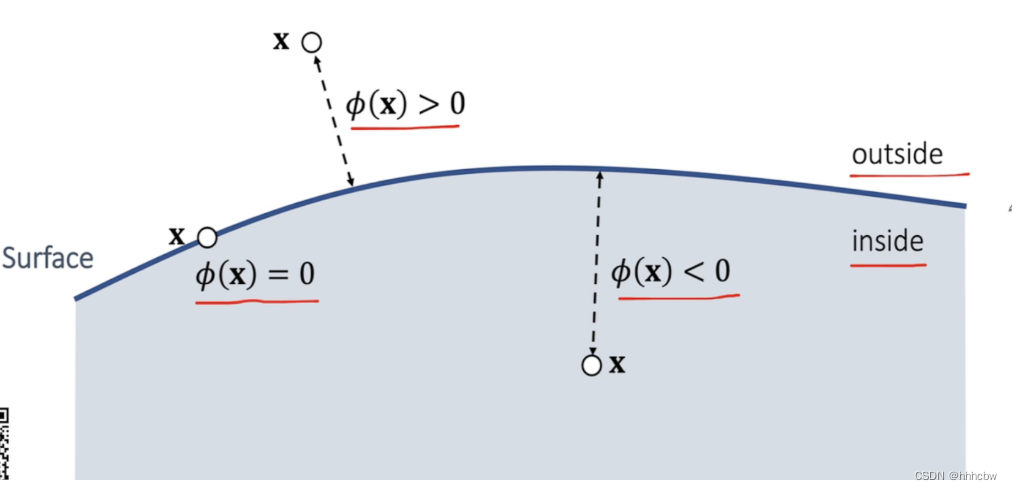
常见的 $\varphi (\vec{x})$ 的实例

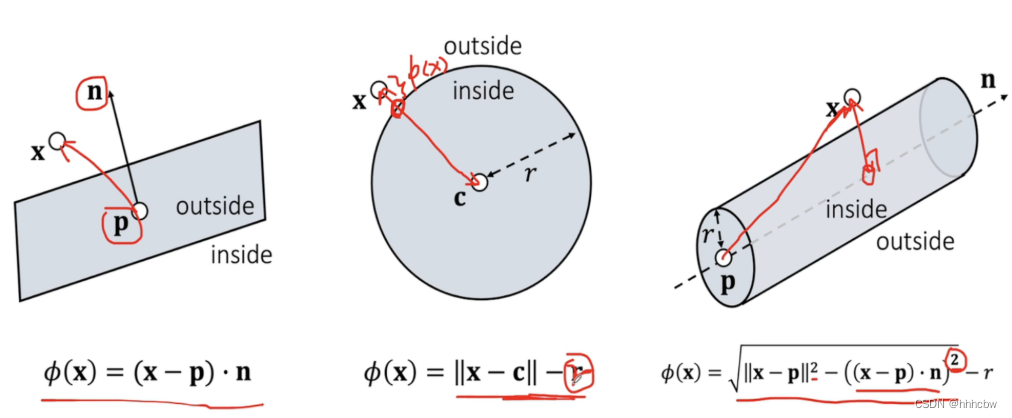
碰撞响应

Penalty Methods

Quadratic Penalty Method

一个 penalty 方法会在下一次更新中应用一次穿透力，即这次更新穿透还是发生了，我们在下一次更新时进行纠正。

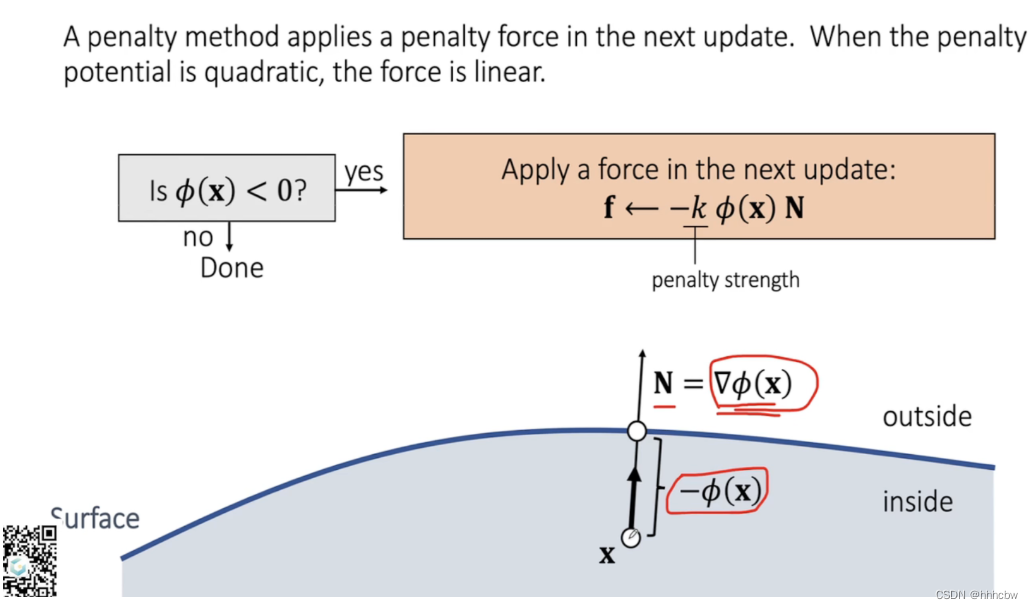
Quadratic Penalty Method with a Buffer

上一个方法的问题在于穿透已经实际产生了，我们可以加一个缓冲区，在穿透还未发生时阻止其产生。需要注意的 k 的大小设置很重要，如果 k 太小穿透仍会发生，而 k 过大会产生 overshooting 问题，即受到的穿透力过大导致物体飞出去。

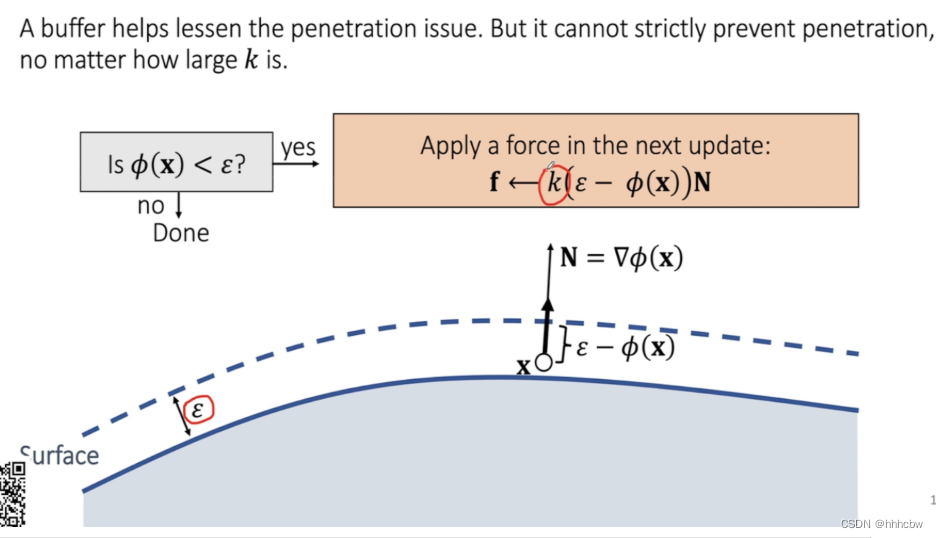
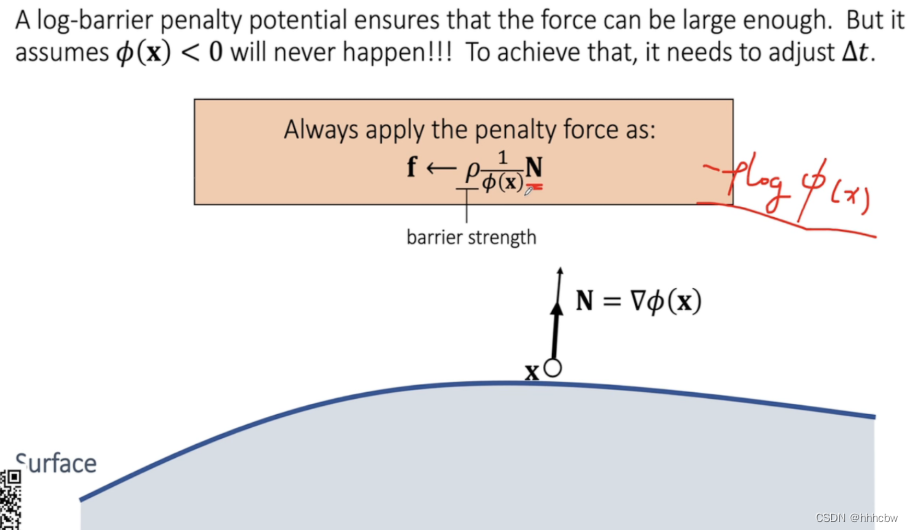
Log-Barrier Penalty Method

使用log-barrier penalty 能确保力足够大，但是仍存在overshooting问题，且需要保证 $\varphi (\vec{x})<0$ 不会发生，否则会导致发生穿透越陷越深。

Impulse Method

Impulse 方法假设碰撞会立即改变位置与速度


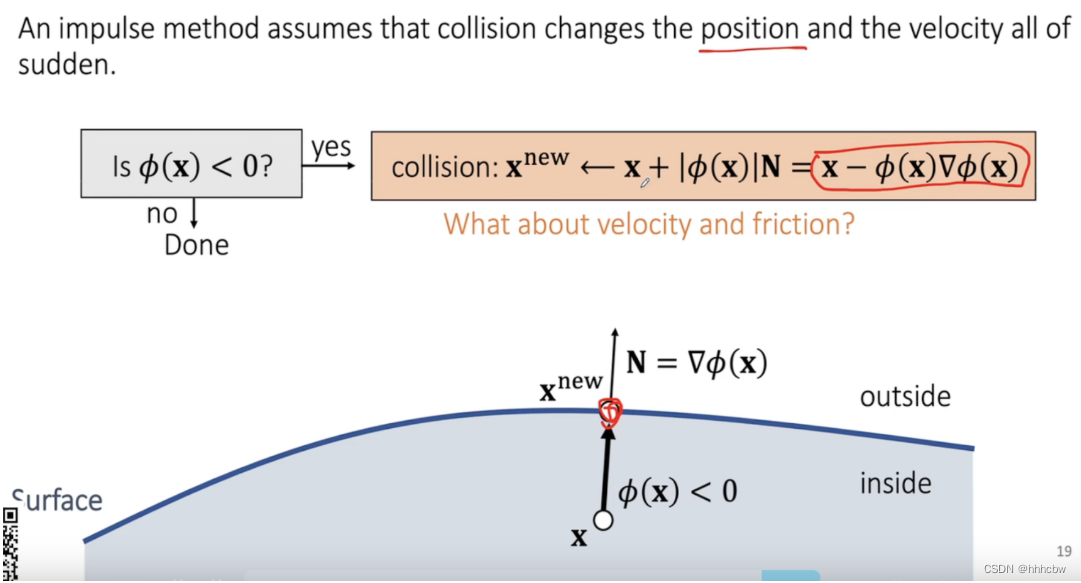
我们可以把当前速度看成与碰撞平面法向量相同的法向速度$\overrightarrow{v_N}$，以及相切的切向速度$\overrightarrow{v_T}$。对于法向速度，我们要将其反向且乘上一个摩擦系数，因为会有损耗，切向速度也要乘上摩擦系数。

而摩擦系数与新速度和旧速度之间的关系要满足 Coulomb’s law，因此 a 可以如上图求出。

---

刚体碰撞检测与响应

碰撞检测

与粒子的碰撞检测相同，刚体可以看作很多粒子组成的系统，那么我们就对所有粒子进行粒子的碰撞检测。

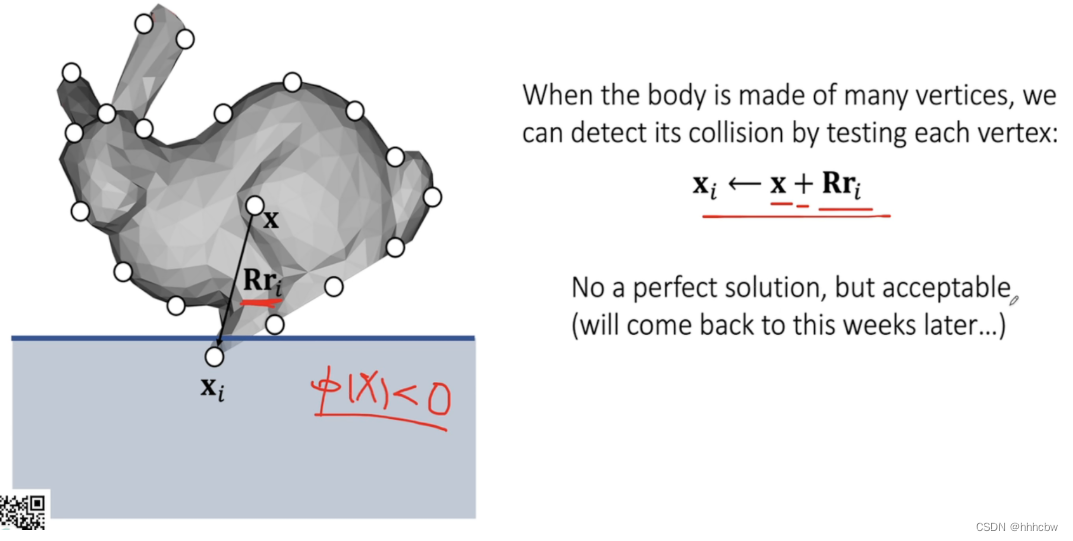
Impulse方法的碰撞响应

我们可以按照粒子的 Impulse 方法的碰撞响应来进行，但是我们不能直接对速度进行更新(按照老师的话其只是一个中间变量)，因为我们对于速度的更新是分为平移速度和角速度的，我们要想办法转为对这两个量的更新。

向量叉乘可以转化为对应的矩阵乘向量

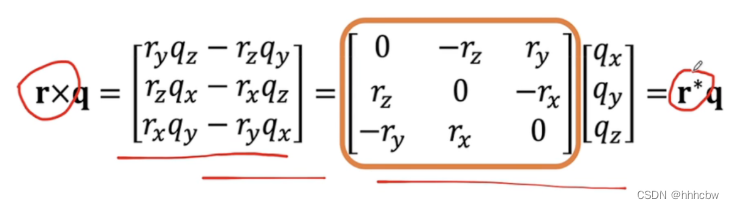
其整体流程如下

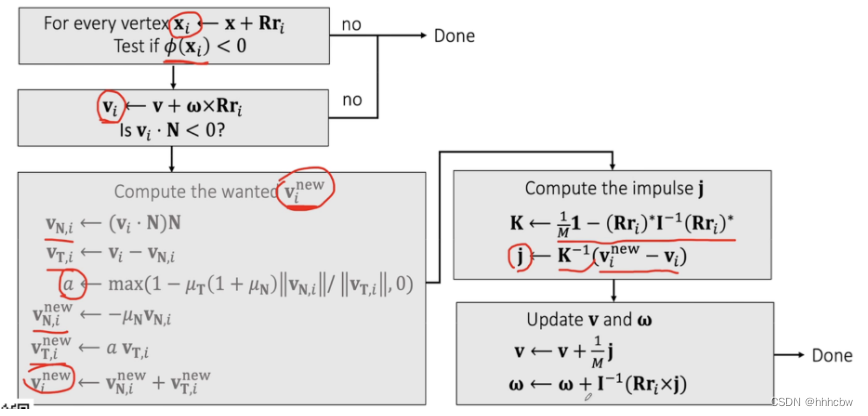
需要注意的是，我们要对所有碰撞的点求平均位置与平均速度来进行后续计算。这里不直接更新位置的原因是，这个问题是非线性的，之后会约束的章节讨论。

---

作业代码与提高项

Unity 2021.3.21f1c1

作业代码

using UnityEngine;
using System.Collections;
using System;

public class Rigid_Bunny : MonoBehaviour
{
    bool launched = false;
    float dt = 0.015f;
    Vector3 v = new Vector3(0, 0, 0);   // velocity
    Vector3 w = new Vector3(0, 0, 0);   // angular velocity

    float mass;                                 // mass
    Matrix4x4 I_ref;                            // reference inertia

    float linear_decay = 0.999f;                // for velocity decay
    float angular_decay = 0.98f;
    float restitution = 0.5f;                 // for collision
    float friction = 0.2f;                  

    Vector3 gravity = new Vector3(0.0f, -9.8f, 0.0f);


    // Use this for initialization
    void Start()
    {
        Mesh mesh = GetComponent<MeshFilter>().mesh;
        Vector3[] vertices = mesh.vertices;

        float m = 1;
        mass = 0;
        for (int i = 0; i < vertices.Length; i++)
        {
            mass += m;
            float diag = m * vertices[i].sqrMagnitude;//diag = mv^2
            I_ref[0, 0] += diag;
            I_ref[1, 1] += diag;
            I_ref[2, 2] += diag;
            I_ref[0, 0] -= m * vertices[i][0] * vertices[i][0];
            I_ref[0, 1] -= m * vertices[i][0] * vertices[i][1];
            I_ref[0, 2] -= m * vertices[i][0] * vertices[i][2];
            I_ref[1, 0] -= m * vertices[i][1] * vertices[i][0];
            I_ref[1, 1] -= m * vertices[i][1] * vertices[i][1];
            I_ref[1, 2] -= m * vertices[i][1] * vertices[i][2];
            I_ref[2, 0] -= m * vertices[i][2] * vertices[i][0];
            I_ref[2, 1] -= m * vertices[i][2] * vertices[i][1];
            I_ref[2, 2] -= m * vertices[i][2] * vertices[i][2];
        }
        I_ref[3, 3] = 1;
    }

    Matrix4x4 Get_Cross_Matrix(Vector3 a)//得到向量a的叉乘矩阵
    {
        //Get the cross product matrix of vector a
        Matrix4x4 A = Matrix4x4.zero;
        A[0, 0] = 0;
        A[0, 1] = -a[2];
        A[0, 2] = a[1];
        A[1, 0] = a[2];
        A[1, 1] = 0;
        A[1, 2] = -a[0];
        A[2, 0] = -a[1];
        A[2, 1] = a[0];
        A[2, 2] = 0;
        A[3, 3] = 1;
        return A;
    }

    private Quaternion Add(Quaternion a, Quaternion b)
    {
        a.x += b.x;
        a.y += b.y;
        a.z += b.z;
        a.w += b.w;
        return a;
    }

    private Matrix4x4 Matrix_subtraction(Matrix4x4 a, Matrix4x4 b)
    {
        for (int i = 0; i < 4; ++i)
        {
            for (int j = 0; j < 4; ++j)
            {
                a[i, j] -= b[i, j];
            }
        }
        return a;
    }


    private Matrix4x4 Matrix_miltiply_float(Matrix4x4 a, float b)
    {
        for (int i = 0; i < 4; ++i)
        {
            for (int j = 0; j < 4; ++j)
            {
                a[i, j] *= b;
            }
        }
        return a;
    }

    // In this function, update v and w by the impulse due to the collision with
    // a plane <P, N>
    void Collision_Impulse(Vector3 P, Vector3 N)
    {
        Mesh mesh = GetComponent<MeshFilter>().mesh;
        Vector3[] vertices = mesh.vertices;

        Matrix4x4 R = Matrix4x4.Rotate(transform.rotation);  // rotation matrix
        Vector3 T = transform.position;                     // translation vector

        Vector3 sum = new Vector3(0, 0, 0);                 
        int collisionNum = 0;                               // number of collision


        for (int i = 0; i < vertices.Length; i++)
        {
            Vector3 r_i = vertices[i];
            Vector3 Rri = R.MultiplyVector(r_i);
            Vector3 x_i = T + Rri;
            float d = Vector3.Dot(x_i - P, N);
            if (d < 0.0f) // collision occur
            {
                Vector3 v_i = v + Vector3.Cross(w, Rri);
                float v_N_size = Vector3.Dot(v_i, N);
                // check velocity
                if (v_N_size < 0.0f)
                {
                    sum += r_i;
                    collisionNum++;
                }
            }
        }

        if (collisionNum == 0) return;
        Matrix4x4 I_rot = R * I_ref * R.transpose;
        Matrix4x4 I_inverse = I_rot.inverse;      
        Vector3 r_collision = sum / (float)collisionNum;                // virtual collision point（local coordination）
        Vector3 Rr_collision = R.MultiplyVector(r_collision);
        //Vector3 x_collision = T + Rr_collision;							 // virtual collision point（global coordination）
        Vector3 v_collision = v + Vector3.Cross(w, Rr_collision);
        
        // Compute the wanted v_N
        Vector3 v_N = Vector3.Dot(v_collision, N) * N;
        Vector3 v_T = v_collision - v_N;
        Vector3 v_N_new = -1.0f * restitution * v_N;
        float a = Math.Max(1.0f - friction * (1.0f + restitution) * v_N.magnitude / v_T.magnitude, 0.0f);
        Vector3 v_T_new = a * v_T;
        Vector3 v_new = v_N_new + v_T_new;
        
        // Compute the impulse J
        Matrix4x4 Rri_star = Get_Cross_Matrix(Rr_collision);
        Matrix4x4 K = Matrix_subtraction(Matrix_miltiply_float(Matrix4x4.identity, 1.0f / mass),
                                        Rri_star * I_inverse * Rri_star);
        Vector3 J = K.inverse.MultiplyVector(v_new - v_collision);
        
        // Update v and w with impulse J
        v = v + 1.0f / mass * J;
        w = w + I_inverse.MultiplyVector(Vector3.Cross(Rr_collision, J));
    }

    // Update is called once per frame
    void Update()
    {
        //Game Control
        if (Input.GetKey("r"))
        {
            // return initial state
            transform.position = new Vector3(0, 0.6f, 0);
            transform.eulerAngles = new Vector3(80, 0, 0);
            restitution = 0.5f;
            launched = false;
            Debug.Log("return to origin");
        }
        if (Input.GetKey("l"))
        {
            v = new Vector3(5, 2, 0);
            w = new Vector3(0, 1, 0);
            launched = true;
        }

        if (launched)
        {
            // Part I: Update velocities
            v += dt * gravity;
            v *= linear_decay;
            w *= angular_decay;

            // Part II: Collision Impulse
            Collision_Impulse(new Vector3(0, 0.01f, 0), new Vector3(0, 1, 0));
            Collision_Impulse(new Vector3(2, 0, 0), new Vector3(-1, 0, 0));

            // Part III: Update position & orientation
            Vector3 x_0 = transform.position;
            Quaternion q_0 = transform.rotation;
            //Update linear status
            Vector3 x = x_0 + dt * v;
            //Update angular status
            Vector3 dw = 0.5f * dt * w;
            Quaternion qw = new Quaternion(dw.x, dw.y, dw.z, 0.0f);
            Quaternion q = Add(q_0, qw * q_0);

            // Part IV: Assign to the object
            transform.position = x;
            transform.rotation = q;
        }
    }
}

运行结果

提高项

Shape Matching的思想是将刚体看作粒子系统，针对每个粒子有其自己的位置与速度，分别对每个粒子进行更新。之后对更新后的粒子，使用刚体的约束进行修复。这里的刚体约束就是每个粒子的位置，由质心坐标与其相对于质心的矢量以及旋转矩阵R有关，即$\overrightarrow{x_i}=\vec{c}+R\overrightarrow{r_i}$。要让约束后的位置和初始位置 $y_i$ 尽可能接近。


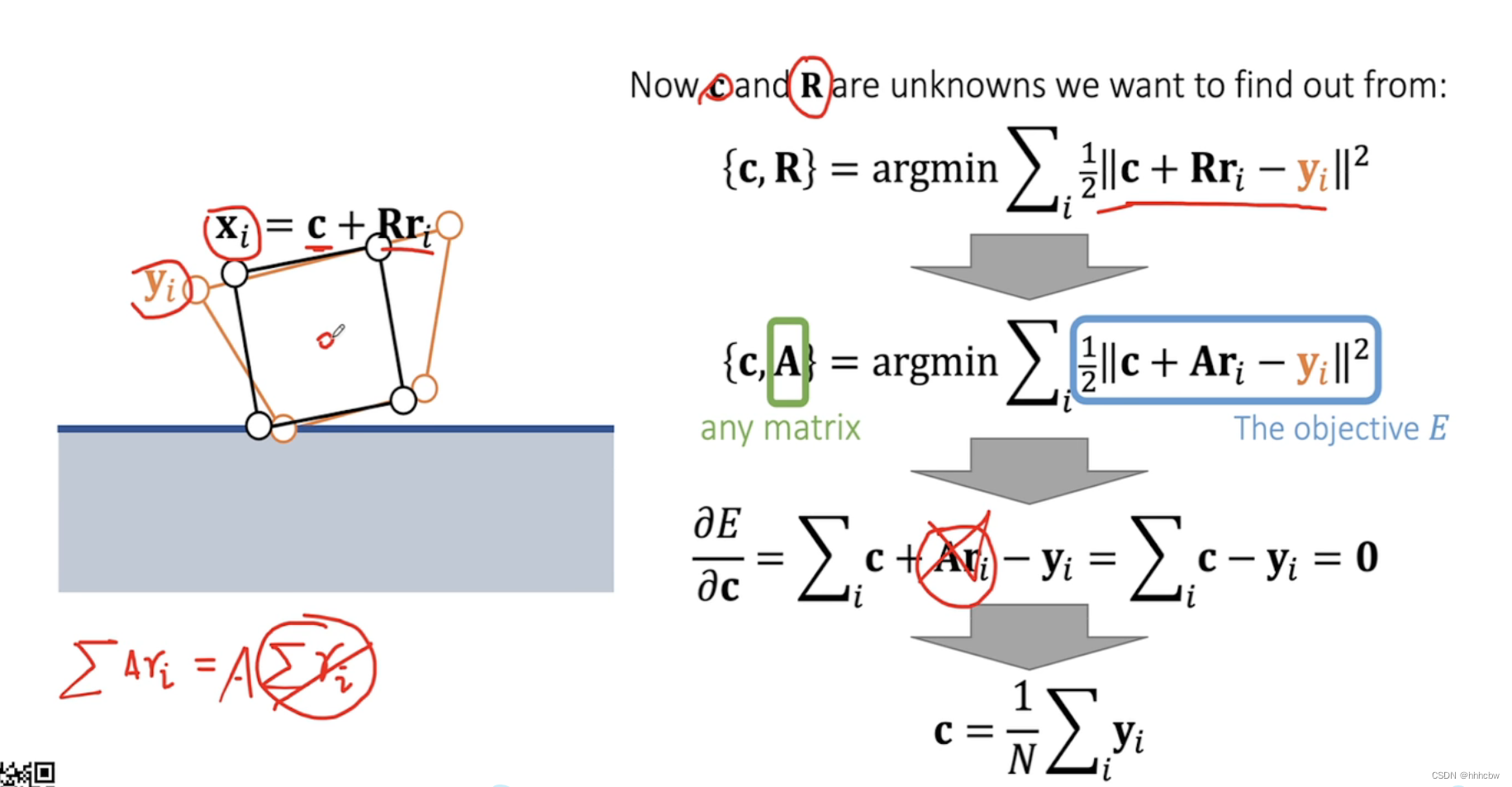
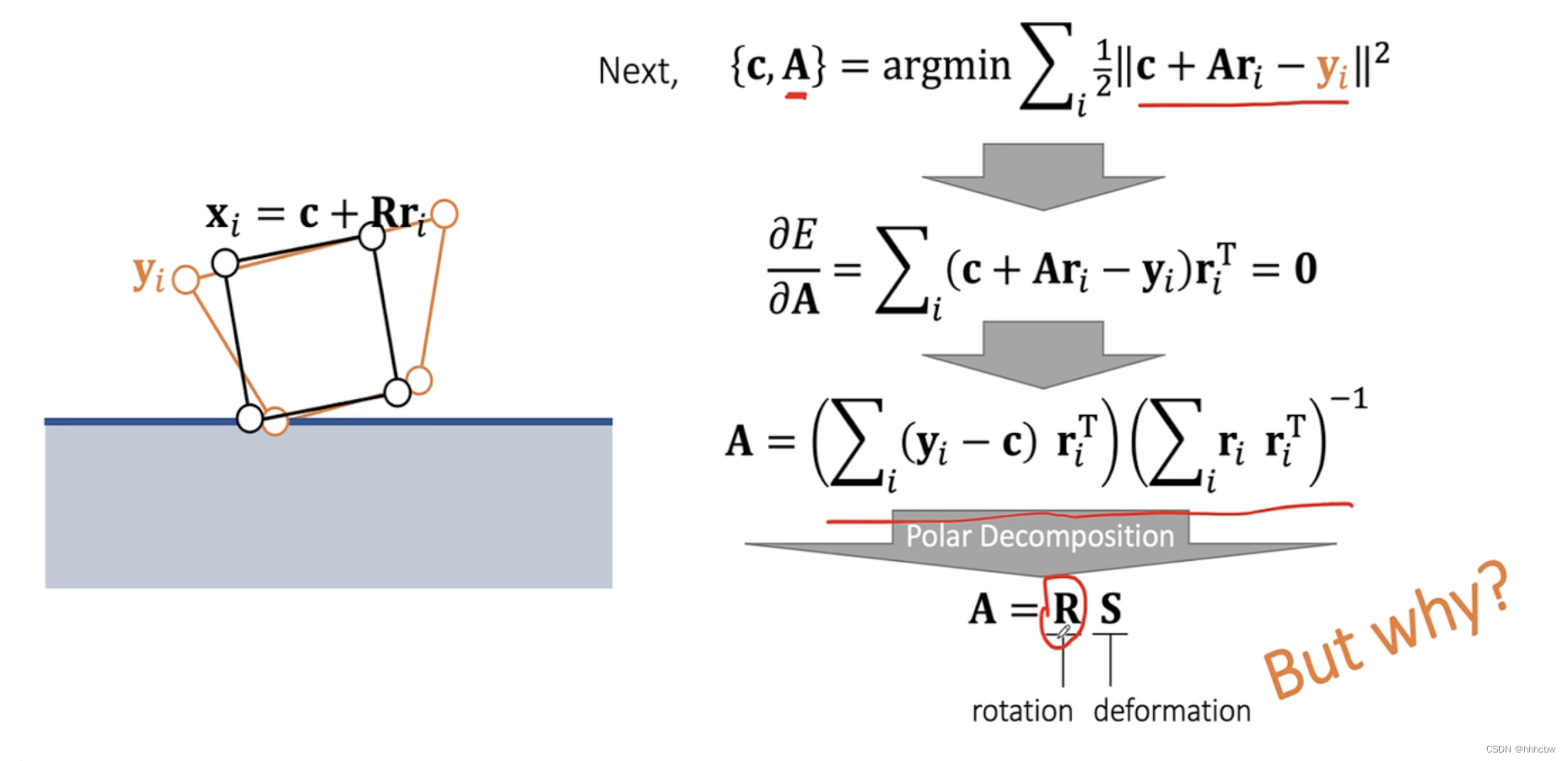
其更新过程如下

对于粒子的碰撞响应，采用之前impulse的方法，但是直接更新其法向速度和切向速度。

代码如下

using System;
using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class Rigid_Bunny_by_Shape_Matching : MonoBehaviour
{
    public bool launched = false;
    Vector3[] X;
    Vector3[] Q;
    Vector3[] V;
    Vector3[] Y;
    Matrix4x4 QQt = Matrix4x4.zero;
    Vector3 gravity = new Vector3(0, -9.8f, 0);
    float linear_decay = 0.999f; // for velocity decay
    float restitution = 5.0f; // for collision
    float friction = 0.5f;

    // Start is called before the first frame update
    void Start()
    {
        Mesh mesh = GetComponent<MeshFilter>().mesh;
        V = new Vector3[mesh.vertices.Length];
        Y = mesh.vertices;
        X = mesh.vertices;
        Q = mesh.vertices;

        //Centerizing Q.
        Vector3 c = Vector3.zero;
        for (int i = 0; i < Q.Length; i++)
            c += Q[i];
        c /= Q.Length;
        //Debug.Log(c);
        for (int i = 0; i < Q.Length; i++)
            Q[i] -= c;

        //Get QQ^t ready.
        for (int i = 0; i < Q.Length; i++)
        {
            QQt[0, 0] += Q[i][0] * Q[i][0];
            QQt[0, 1] += Q[i][0] * Q[i][1];
            QQt[0, 2] += Q[i][0] * Q[i][2];
            QQt[1, 0] += Q[i][1] * Q[i][0];
            QQt[1, 1] += Q[i][1] * Q[i][1];
            QQt[1, 2] += Q[i][1] * Q[i][2];
            QQt[2, 0] += Q[i][2] * Q[i][0];
            QQt[2, 1] += Q[i][2] * Q[i][1];
            QQt[2, 2] += Q[i][2] * Q[i][2];
        }
        QQt[3, 3] = 1;

        for (int i = 0; i < X.Length; i++)
            V[i][0] = 4.0f;

        //Debug.Log(transform.position);
        // transform X from local coordination to global coordination
        Update_Mesh(transform.position, Matrix4x4.Rotate(transform.rotation), 0);
        transform.position = Vector3.zero;
        transform.rotation = Quaternion.identity;
        //Debug.Log(transform.position);
    }

    // Polar Decomposition that returns the rotation from F.
    Matrix4x4 Get_Rotation(Matrix4x4 F)
    {
        Matrix4x4 C = Matrix4x4.zero;
        for (int ii = 0; ii < 3; ii++)
            for (int jj = 0; jj < 3; jj++)
                for (int kk = 0; kk < 3; kk++)
                    C[ii, jj] += F[kk, ii] * F[kk, jj];

        Matrix4x4 C2 = Matrix4x4.zero;
        for (int ii = 0; ii < 3; ii++)
            for (int jj = 0; jj < 3; jj++)
                for (int kk = 0; kk < 3; kk++)
                    C2[ii, jj] += C[ii, kk] * C[jj, kk];

        float det = F[0, 0] * F[1, 1] * F[2, 2] +
                        F[0, 1] * F[1, 2] * F[2, 0] +
                        F[1, 0] * F[2, 1] * F[0, 2] -
                        F[0, 2] * F[1, 1] * F[2, 0] -
                        F[0, 1] * F[1, 0] * F[2, 2] -
                        F[0, 0] * F[1, 2] * F[2, 1];

        float I_c = C[0, 0] + C[1, 1] + C[2, 2];
        float I_c2 = I_c * I_c;
        float II_c = 0.5f * (I_c2 - C2[0, 0] - C2[1, 1] - C2[2, 2]);
        float III_c = det * det;
        float k = I_c2 - 3 * II_c;

        Matrix4x4 inv_U = Matrix4x4.zero;
        if (k < 1e-10f)
        {
            float inv_lambda = 1 / Mathf.Sqrt(I_c / 3);
            inv_U[0, 0] = inv_lambda;
            inv_U[1, 1] = inv_lambda;
            inv_U[2, 2] = inv_lambda;
        }
        else
        {
            float l = I_c * (I_c * I_c - 4.5f * II_c) + 13.5f * III_c;
            float k_root = Mathf.Sqrt(k);
            float value = l / (k * k_root);
            if (value < -1.0f) value = -1.0f;
            if (value > 1.0f) value = 1.0f;
            float phi = Mathf.Acos(value);
            float lambda2 = (I_c + 2 * k_root * Mathf.Cos(phi / 3)) / 3.0f;
            float lambda = Mathf.Sqrt(lambda2);

            float III_u = Mathf.Sqrt(III_c);
            if (det < 0) III_u = -III_u;
            float I_u = lambda + Mathf.Sqrt(-lambda2 + I_c + 2 * III_u / lambda);
            float II_u = (I_u * I_u - I_c) * 0.5f;


            float inv_rate, factor;
            inv_rate = 1 / (I_u * II_u - III_u);
            factor = I_u * III_u * inv_rate;

            Matrix4x4 U = Matrix4x4.zero;
            U[0, 0] = factor;
            U[1, 1] = factor;
            U[2, 2] = factor;

            factor = (I_u * I_u - II_u) * inv_rate;
            for (int i = 0; i < 3; i++)
                for (int j = 0; j < 3; j++)
                    U[i, j] += factor * C[i, j] - inv_rate * C2[i, j];

            inv_rate = 1 / III_u;
            factor = II_u * inv_rate;
            inv_U[0, 0] = factor;
            inv_U[1, 1] = factor;
            inv_U[2, 2] = factor;

            factor = -I_u * inv_rate;
            for (int i = 0; i < 3; i++)
                for (int j = 0; j < 3; j++)
                    inv_U[i, j] += factor * U[i, j] + inv_rate * C[i, j];
        }

        Matrix4x4 R = Matrix4x4.zero;
        for (int ii = 0; ii < 3; ii++)
            for (int jj = 0; jj < 3; jj++)
                for (int kk = 0; kk < 3; kk++)
                    R[ii, jj] += F[ii, kk] * inv_U[kk, jj];
        R[3, 3] = 1;
        return R;
    }

    // Update the mesh vertices according to translation c and rotation R.
    // It also updates the velocity.
    void Update_Mesh(Vector3 c, Matrix4x4 R, float inv_dt)
    {
        for (int i = 0; i < Q.Length; i++)
        {
            Vector3 x = (Vector3)(R * Q[i]) + c;

            V[i] = (x - X[i]) * inv_dt;
            X[i] = x;
        }
        Mesh mesh = GetComponent<MeshFilter>().mesh;
        mesh.vertices = X;
    }

    void Collision(float inv_dt)
    {
        Vector3 P = new Vector3(0, 0.01f, 0);
        Vector3 N = new Vector3(0, 1, 0);
        // check collision with ground
        for (int i = 0; i < X.Length; i++)
        {
            float d = Vector3.Dot(X[i] - P, N);
            if (d < 0.0f) // collision occur
            {
                float v_N_size = Vector3.Dot(V[i], N);
                // check velocity
                if (v_N_size < 0.0f)
                {
                    Vector3 v_N = v_N_size * N;
                    Vector3 v_T = V[i] - v_N;
                    Vector3 v_N_new = -1.0f * restitution * v_N;
                    float a = Math.Max(1.0f - friction * (1.0f + restitution) * v_N.magnitude / v_T.magnitude, 0.0f);
                    Vector3 v_T_new = a * v_T;
                    V[i] = v_N_new + v_T_new;
                }
            }
        }

        P = new Vector3(2.01f, 0, 0);
        N = new Vector3(-1, 0, 0);
        // check collsion with wall
        for (int i = 0; i < X.Length; i++)
        {
            float d = Vector3.Dot(X[i] - P, N);
            if (d < 0.0f) // collision occur
            {
                float v_N_size = Vector3.Dot(V[i], N);
                // check velocity
                if (v_N_size < 0.0f)
                {
                    Vector3 v_N = v_N_size * N;
                    Vector3 v_T = V[i] - v_N;
                    Vector3 v_N_new = -1.0f * restitution * v_N;
                    float a = Math.Max(1.0f - friction * (1.0f + restitution) * v_N.magnitude / v_T.magnitude, 0.0f);
                    Vector3 v_T_new = a * v_T;
                    V[i] = v_N_new + v_T_new;
                }
            }
        }
    }

    Matrix4x4 Vector3_mul_Vector3T(Vector3 v1, Vector3 v2)
    {
        Matrix4x4 res = Matrix4x4.zero;
        res[3, 3] = 1.0f;
        for (int i = 0; i < 3; i++)
            for (int j = 0; j < 3; j++)
            {
                res[i, j] = v1[i] * v2[j];
            }
        return res;
    }

    Matrix4x4 Matrix4x4_add_Matrix4x4(Matrix4x4 m1, Matrix4x4 m2)
    {
        Matrix4x4 res = Matrix4x4.zero;
        for (int i = 0; i < 3; i++)
            for (int j = 0; j < 3; j++)
            {
                res[i, j] = m1[i, j] + m2[i, j];
            }
        return res;
    }

    // Update is called once per frame
    void Update()
    {
        //Game Control
        if (Input.GetKey("r"))
        {
            // return initial state
            launched = false;
            for (int i = 0; i < V.Length; i++)
            {
                V[i] = new Vector3(4.0f, 0.0f, 0.0f);
            }
            Update_Mesh(new Vector3(0, 0.6f, 0),
                        Matrix4x4.Rotate(Quaternion.Euler(new Vector3(80, 0, 0))), 0);
            Debug.Log("return to origin");
        }
        if (Input.GetKey("l"))
        {
            launched = true;
            for (int i = 0; i < V.Length; i++)
            {
                V[i] = new Vector3(5.0f, 2.0f, 0.0f);
            }
        }

        if (!launched)
            return;

        float dt = 0.015f;

        //Step 1: run a simple particle system.
        for (int i = 0; i < V.Length; i++)
        {
            V[i] = V[i] + dt * gravity;
            V[i] = V[i] * linear_decay;
        }

        //Step 2: Perform simple particle collision.
        Collision(1 / dt);

        // Step 3: Use shape matching to get new translation c and 
        // new rotation R. Update the mesh by c and R.
        //Shape Matching (translation)
        for (int i = 0; i < V.Length; i++)
        {
            Y[i] = X[i] + V[i] * dt;
        }
        Vector3 c = Vector3.zero;
        for (int i = 0; i < Y.Length; i++)
        {
            c = c + Y[i];
        }
        c = c / Y.Length;
        //Shape Matching (rotation)
        Matrix4x4 A = Matrix4x4.zero;
        for (int i = 0; i < Y.Length; i++)
        {
            A = Matrix4x4_add_Matrix4x4(A, Vector3_mul_Vector3T(Y[i] - c, Q[i]));
        }
        A[3, 3] = 1.0f;
        A = A * QQt.inverse;
        Matrix4x4 R = Get_Rotation(A);
        //Update_Mesh(c, R, 1/dt);
        Update_Mesh(c, R, 1 / dt);
    }
}

运行结果