城市的 天际线 是从远处观看该城市中所有建筑物形成的轮廓的外部轮廓。给你所有建筑物的位置和高度，请返回 由这些建筑物形成的 天际线 。

每个建筑物的几何信息由数组 buildings 表示，其中三元组 buildings[i] = [lefti, righti, heighti] 表示：

lefti 是第 i 座建筑物左边缘的 x 坐标。
righti 是第 i 座建筑物右边缘的 x 坐标。
heighti 是第 i 座建筑物的高度。
你可以假设所有的建筑都是完美的长方形，在高度为 0 的绝对平坦的表面上。

天际线 应该表示为由 “关键点” 组成的列表，格式 [[x1,y1],[x2,y2],…] ，并按 x 坐标 进行 排序 。关键点是水平线段的左端点。列表中最后一个点是最右侧建筑物的终点，y 坐标始终为 0 ，仅用于标记天际线的终点。此外，任何两个相邻建筑物之间的地面都应被视为天际线轮廓的一部分。

注意：输出天际线中不得有连续的相同高度的水平线。例如 […[2 3], [4 5], [7 5], [11 5], [12 7]…] 是不正确的答案；三条高度为 5 的线应该在最终输出中合并为一个：[…[2 3], [4 5], [12 7], …]

解题思路：
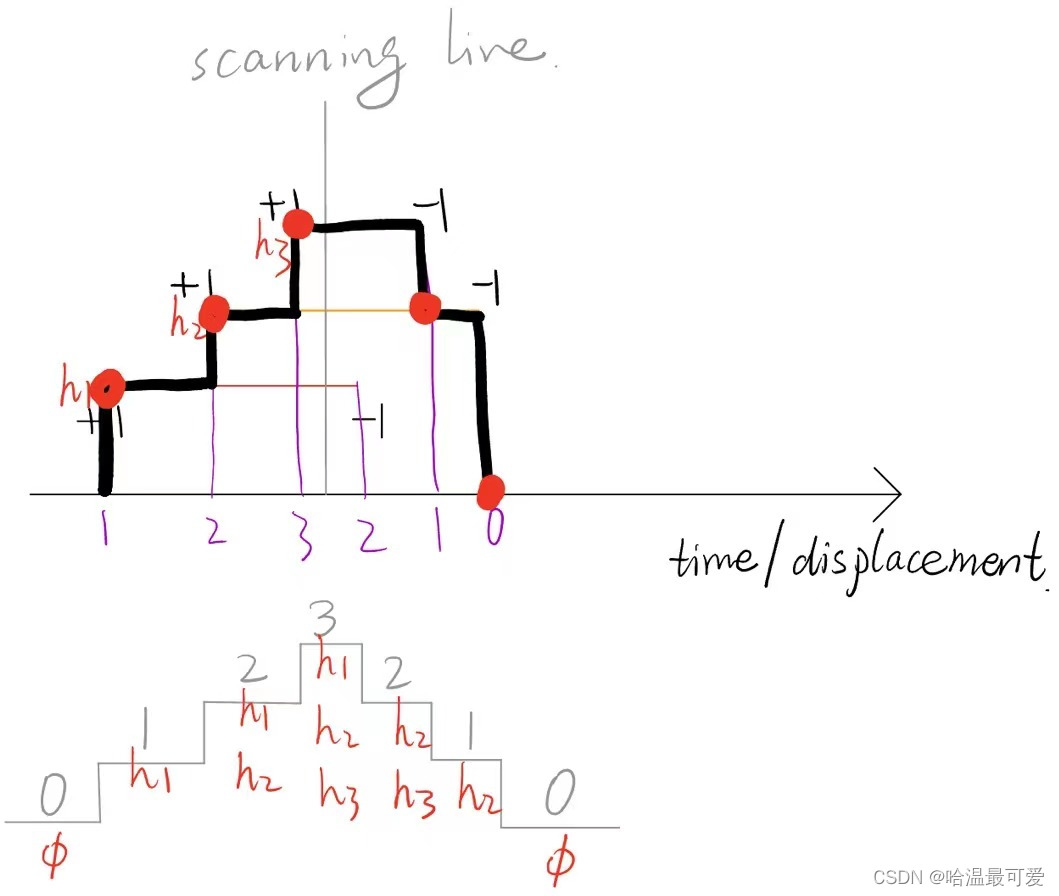
本题可以用“扫描线”解决，一般扫描线是用来求解在某点处被多少区间覆盖。

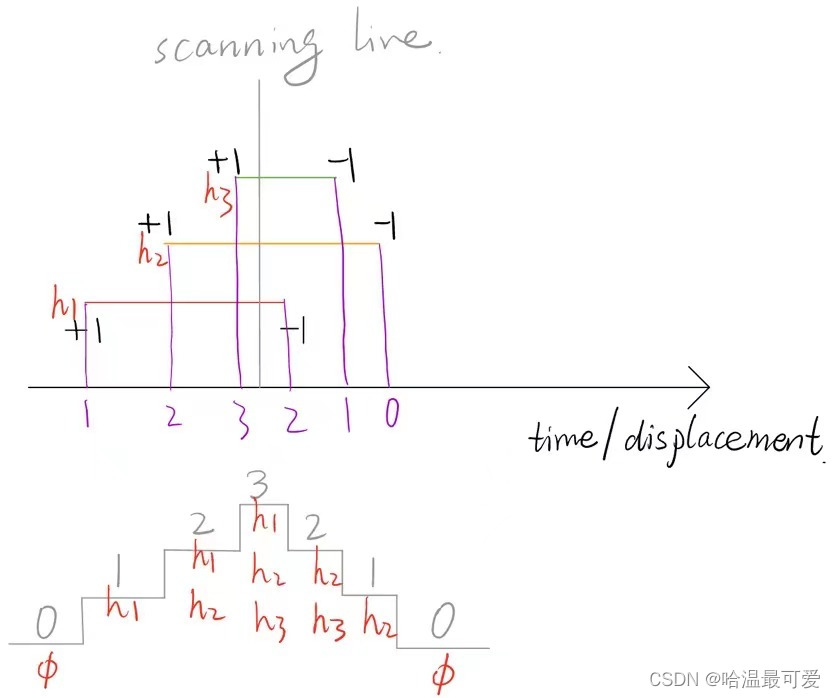
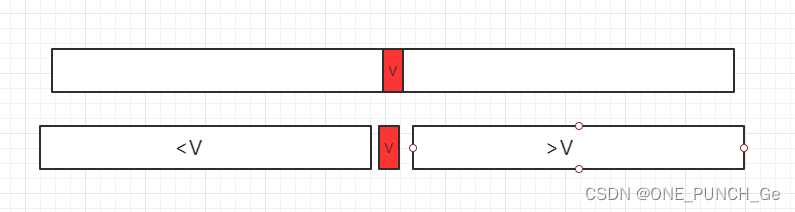
上图中，灰色竖直线为扫描线，它沿着横轴平移，红、黄、绿三条线表示三个区间。扫描线扫过区间左端点，覆盖扫描线的“区间集合”增加一个区间元素；扫描线扫过区间右端点，覆盖扫描线的“区间集合”减少一个区间元素。覆盖扫描线的“区间集合”个数为0时，则覆盖的集合为空集。h1,h2,h3是区间高度值（height value）。

本题中，对于每一幢建筑物，左右端点影响覆盖扫描线“区间集合”的区间元素个数，即遇到左端点区间元素个数加一，遇到右端点区间元素个数减一。但是

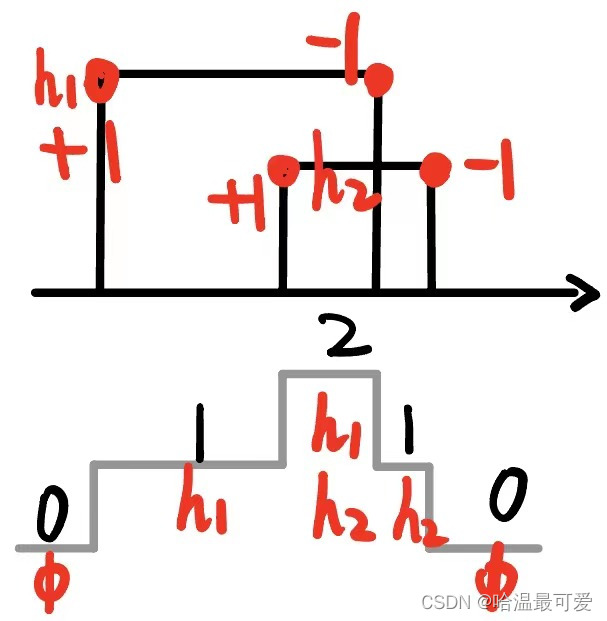
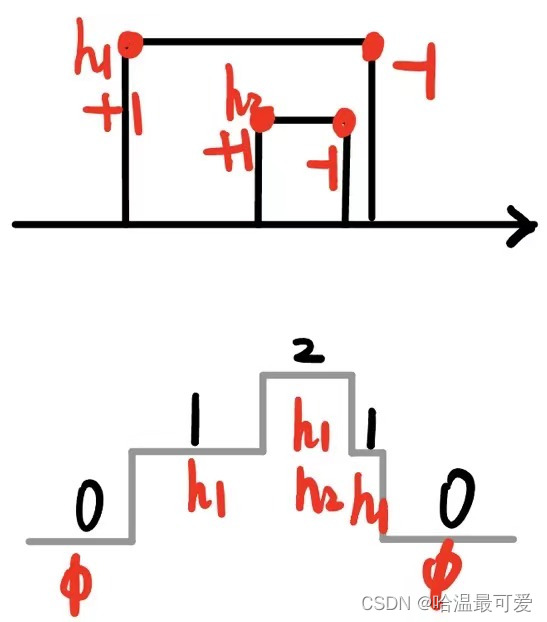
下图中，以建筑物右端点（下降沿）为例，说明了遇到建筑物右端点，区间集合元素的确减少一，但是区间轮廓可能会发生改变，也可能不发生改变。

class Solution {
public:
    vector<vector<int>> getSkyline(vector<vector<int>>& buildings) {
        map<int,vector<pair<int,int>>>  Map;//x position -> {height,flag}
        for(auto building:buildings){
            Map[building[0]].push_back({building[2],1});
            Map[building[1]].push_back({building[2],-1});
        }
        multiset<int> Set;
        vector<vector<int>> ans;
        for(auto& [pos,pairs]:Map){
            for(auto& [height,flag]:pairs){
                if(flag==1)
                    Set.insert(height);
                else
                    Set.erase(Set.find(height));
            }
            int H=Set.empty()? 0:*Set.rbegin();
            if(ans.empty() || ans.back()[1]!=H)
                ans.push_back({pos,H});
        }
        return ans;  
    }
};