目录
前言:
一:解决topk问题
二:堆排序
【1】第一种方法(很少用)
【2】第二种方法(很实用)
前言:
上一次我们进行了二叉树的初步介绍并实现了堆的基本功能,但堆的作用并不是存储数据,它可以用来解决topk问题(求一组数据较大或者较小的前k个)以及对数据进行排序。
附上一期链接:http://t.csdn.cn/pMOia
一:解决topk问题
在讨论topk问题之前我们先来回顾一下堆的性质:
(1)大堆的父亲节点总是大于孩子节点。
(2)小堆的父亲节点总是小于孩子节点。
由此我们可以得到一个结论:
根部节点一定是这个堆的最大或者最小值(大堆为最大,小堆为最小)。
【1】我们可以把所有数据存储在堆中,得到根部的数据后删除根部数据,然后通过调整保持堆的结构,不断重复这个操作直到找到前k个数。
代码(我建立的是大堆,找较大的数):
//初始化 void HeapInit(HP* hp) { //断言,不能传空的结构体指针 assert(hp); hp->a = NULL; //初始化size和容量都为0 hp->size = hp->capacity = 0; } //交换函数 void HeapSwap(int* p1, int* p2) { int tmp = *p1; *p1 = *p2; *p2 = tmp; } void AdjustUp(HPDataType* a, int child) { //断言,不能传空指针 assert(a); //找到父结点的下标 int parent = (child - 1) / 2; //循环,以child到树根为结束条件 while (child > 0) { //如果父结点比child小,交换并更新 if (a[child] > a[parent]) { HeapSwap(&a[child], &a[parent]); child = parent; parent = (child - 1) / 2; } //如果父结点比child大,跳出循环 else { break; } } } //向下调整 void AdjustDown(HPDataType* a, int n, int parent) { //默认左孩子最大 int child = parent * 2 + 1; //当已经调整到超出数组时结束 while (child<n) { //找出两个孩子中大的一方 //考虑右孩子不存在的情况 if (child+1<n&&a[child + 1] > a[child]) { //如果右孩子大,child加1变成右孩子 child++; } //如果父亲比大孩子小,进行调整,否则跳出 if (a[child] > a[parent]) { HeapSwap(&a[child], &a[parent]); //迭代 parent = child; child = parent * 2 + 1; } else { break; } } } //插入数据 void HeapPush(HP* hp, HPDataType x) { if (hp->size == hp->capacity) { //判断扩容多少 int newcapacity = hp->capacity == 0 ? 4 : hp->capacity * 2; //扩容 HPDataType* tmp = (HPDataType*)realloc(hp->a, sizeof(HPDataType) * newcapacity); //更新 hp->capacity = newcapacity; hp->a = tmp; } //存储数据 hp->a[hp->size] = x; hp->size++; //进行调整 AdjustUp(hp->a, hp->size-1); } //打印数据 void HeapPrint(HP* hp) { //断言,不能传空的结构体指针 assert(hp); int i = 0; for (i = 0; i < hp->size; i++) { printf("%d ", hp->a[i]); } printf("\n"); } //删除数据 void HeapPop(HP* hp) { //断言,不能传空的结构体指针 assert(hp); //如果为空,不能删除,避免数组越界 assert(!HeapEmpty(hp)); //不为空,先交换根和最后一片叶子,然后size减1 HeapSwap(&hp->a[0], &hp->a[hp->size - 1]); hp->size--; AdjustDown(hp->a, hp->size, 0); } //取根部数据 HPDataType HeapTop(HP* hp) { return hp->a[0]; }int main() { HP hp; HeapInit(&hp); int arr[20] = { 4,5,6,1,2,44,33,25,69,78,3,0,11,22,77,55,88,75,14,8 }; //找前k个最大的数 int k = 5; for (int i = 0; i < 20; i++) { HeapPush(&hp, arr[i]); } for (int i = 0; i < k; i++) { printf("%d ", HeapTop(&hp)); HeapPop(&hp); } }
缺点:
(1)需要建立一个堆,消耗了额外的空间。
(2)如果要排序的数字很多,内存存储不下。
【2】还有另一种更常用的方法,这个方法只需要建立一个能够存储k个数据的堆。
这里先给结论:
(1)这个方式找较大要建立小堆。
(2)这个方式找较小要建立大堆。
看到这两个结论大家可能会有点懵逼,因为前面找大我就建立大堆,找小我就建立小堆,为什么这里就反过来了呢?先不用着急,我们先讲解一下为什么找较小数要建立大堆。
我们看下面这一组数据:
10 20 58 97 55 66 44
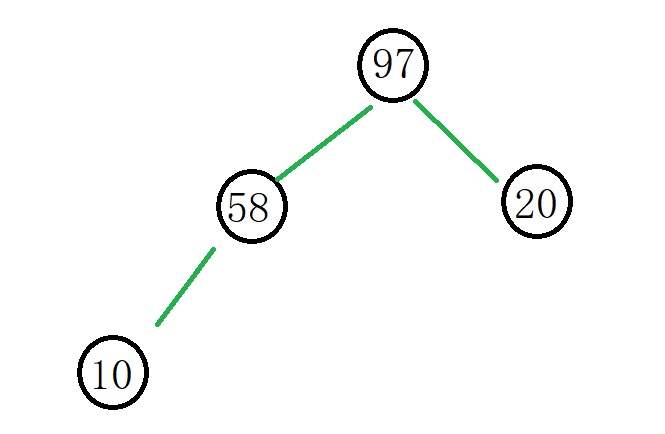
假设我们要找出这些数据中的前4个较小的数据,我们先将前4个数据存储在大堆中,如下:
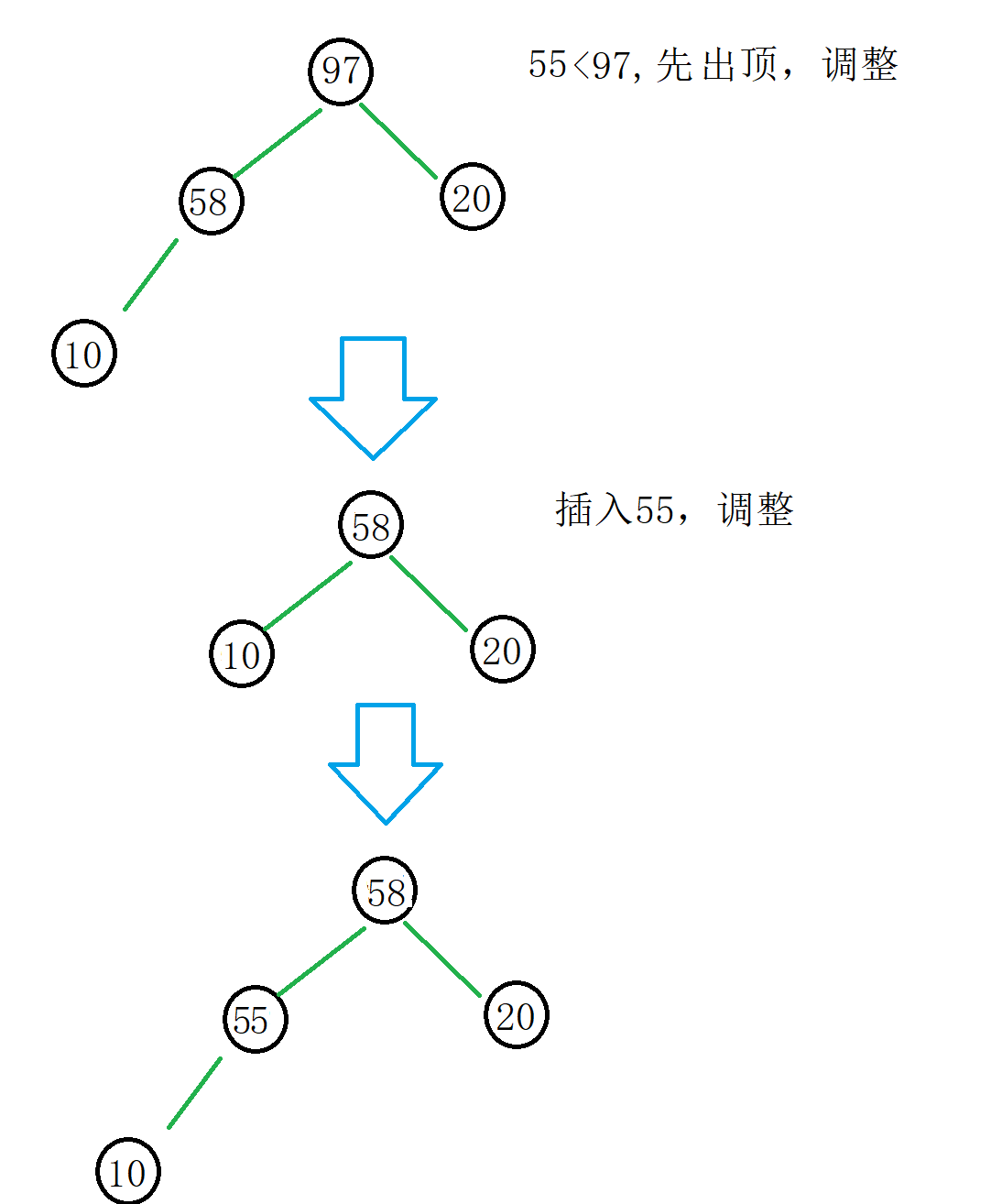
然后我们从55(下标为k)开始遍历,如果数据小于根部,就将堆顶删除,然后将这个数据入堆,调整来保持大堆的结构。
大堆根部数据是堆中最大的数据,我们遍历插入调整的行为其实是不断淘汰数据中较大的元素,一直到遍历结束还在堆中的元素就是前k个较小的值。
我们从55开始遍历替换:
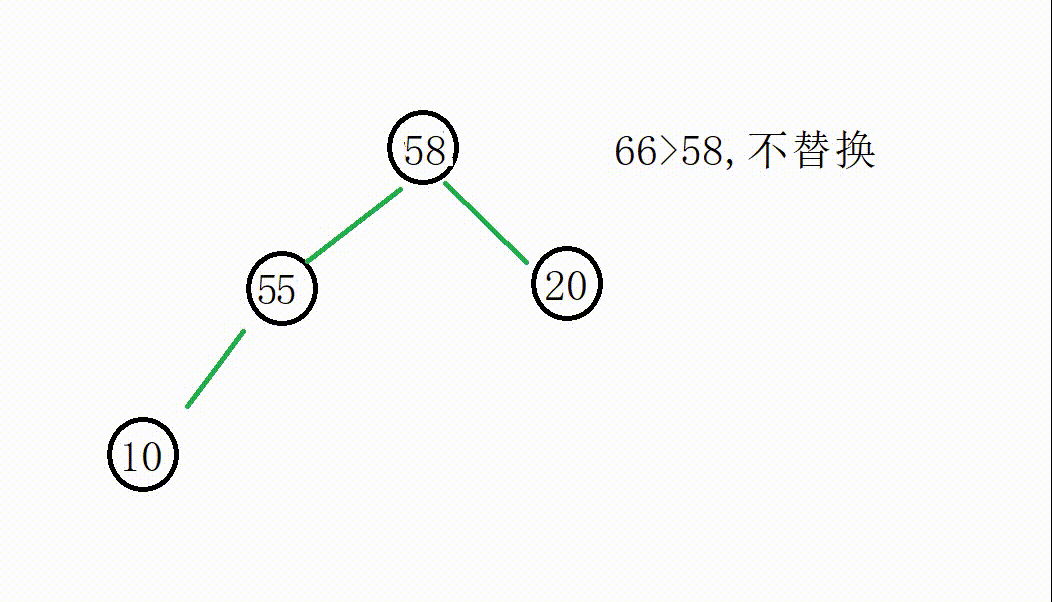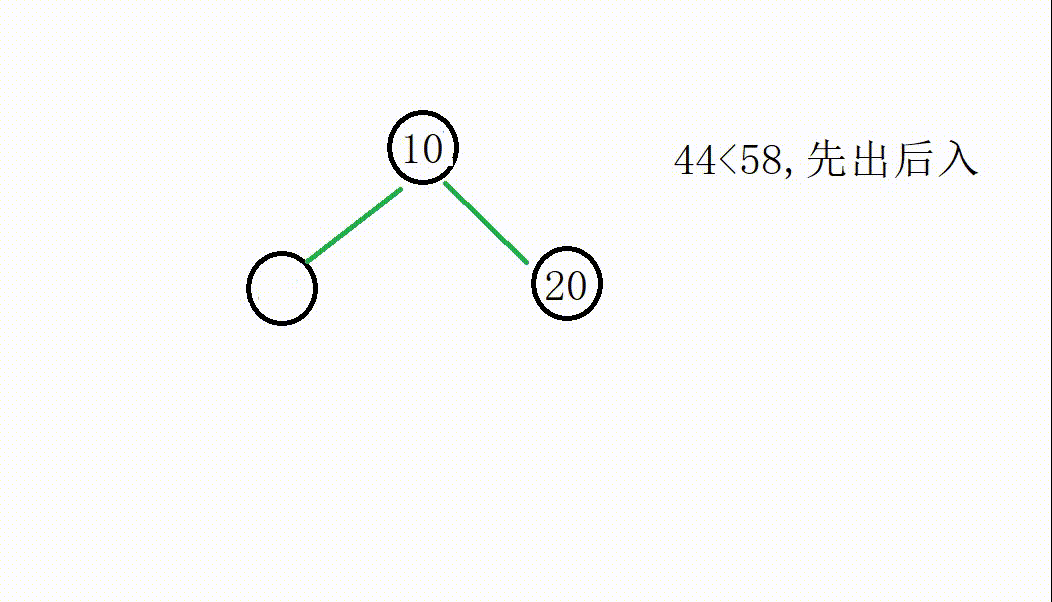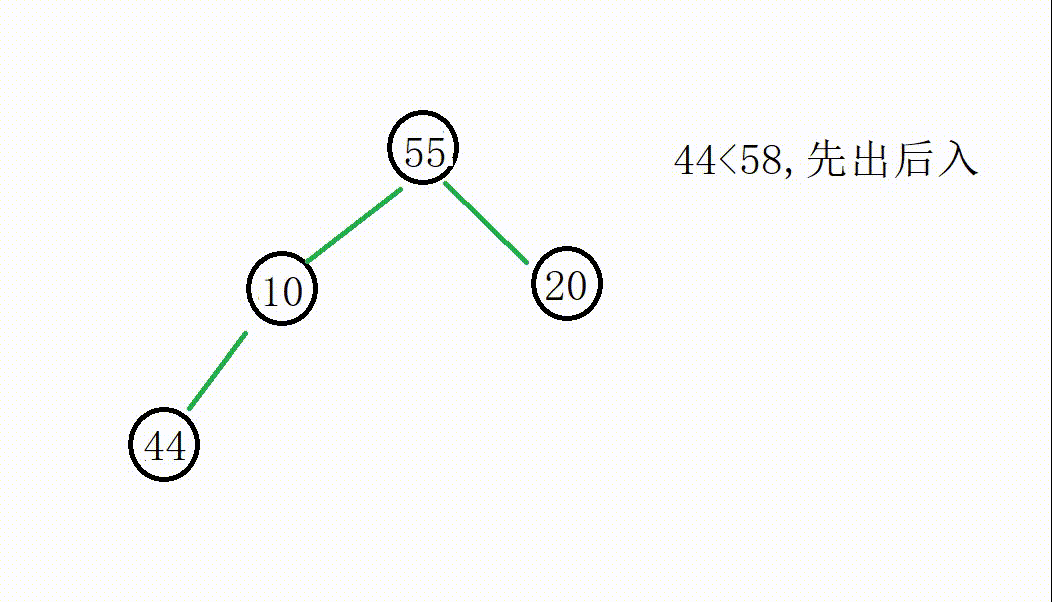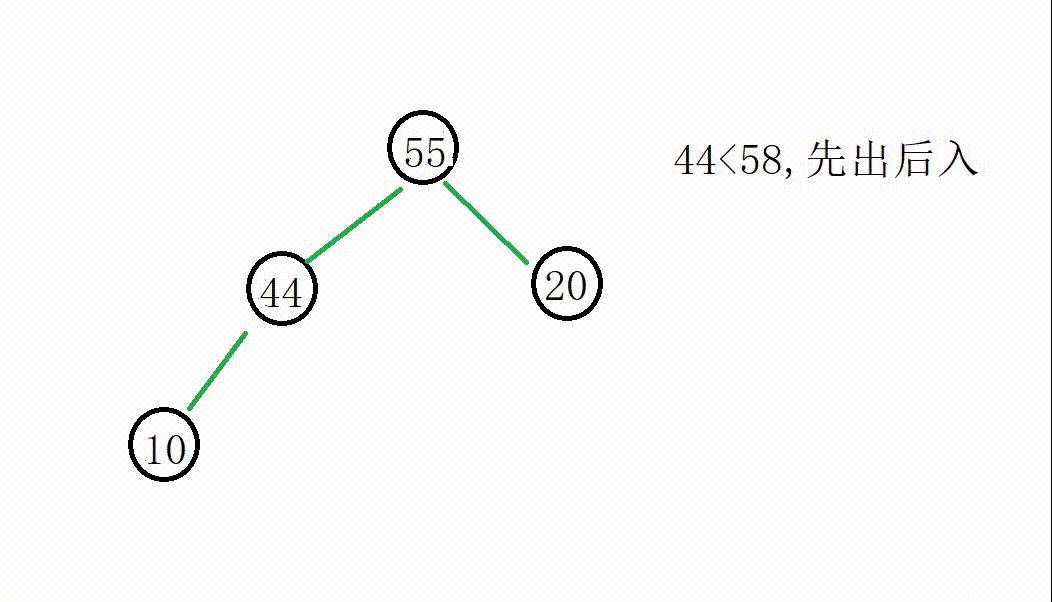
后面的操作一致
最后堆中的元素分别是55,44,10,20,满足了我们的需求。
相反的,如果要求前k个较大的数,我们就建立小堆,遇到比根部大的数据就将堆顶删除,然后将这个数据入堆,调整来保持小堆的结构。
通过遍历插入和调整逐渐淘汰较小的数据,最后堆中的数据就是前k个较大的数据。
为了更好的测试,我们随机生成大量数据求其中的前k个较小数。
代码:
void topk() { HP hp; //堆初始化 HeapInit(&hp); //随机生成一万个数 int n = 10000; //找前五个数 int k = 5; int* a = (int*)malloc(sizeof(int) * n); if (a == NULL) { printf("malloc error\n"); exit(-1); } srand(time(0)); for (int i = 0; i < n; i++) { //随机生成500到1000的数据 a[i] = rand() % (500) + 500; } for (int i = 0; i < k; i++) { //把数组前面几个数拿过来作堆 HeapPush(&hp, a[i]); } //为了方便我们观察,我们设置5个小于500的数据 a[100] = 423; a[888] = 55; a[999] = 450; a[887] = 478; a[56] = 256; for (int i = k; i < n; i++) { //如果a[i]比堆顶小,删除堆顶,然后入堆 if (a[i] < HeapTop(&hp)) { HeapPop(&hp); HeapPush(&hp, a[i]); } } //遍历调整结束,最后堆中元素为最小的前5个 HeapPrint(&hp); }
这个方式的优点:
(1)只需要建立存储k个数据的堆,空间消耗小。
(2)因为是一个个数据进行遍历,可以把数据存储在磁盘中,从磁盘中读取数据。
二:堆排序
【1】第一种方法(很少用)
(1)我们可以建立一个堆,把数据存储在堆中。
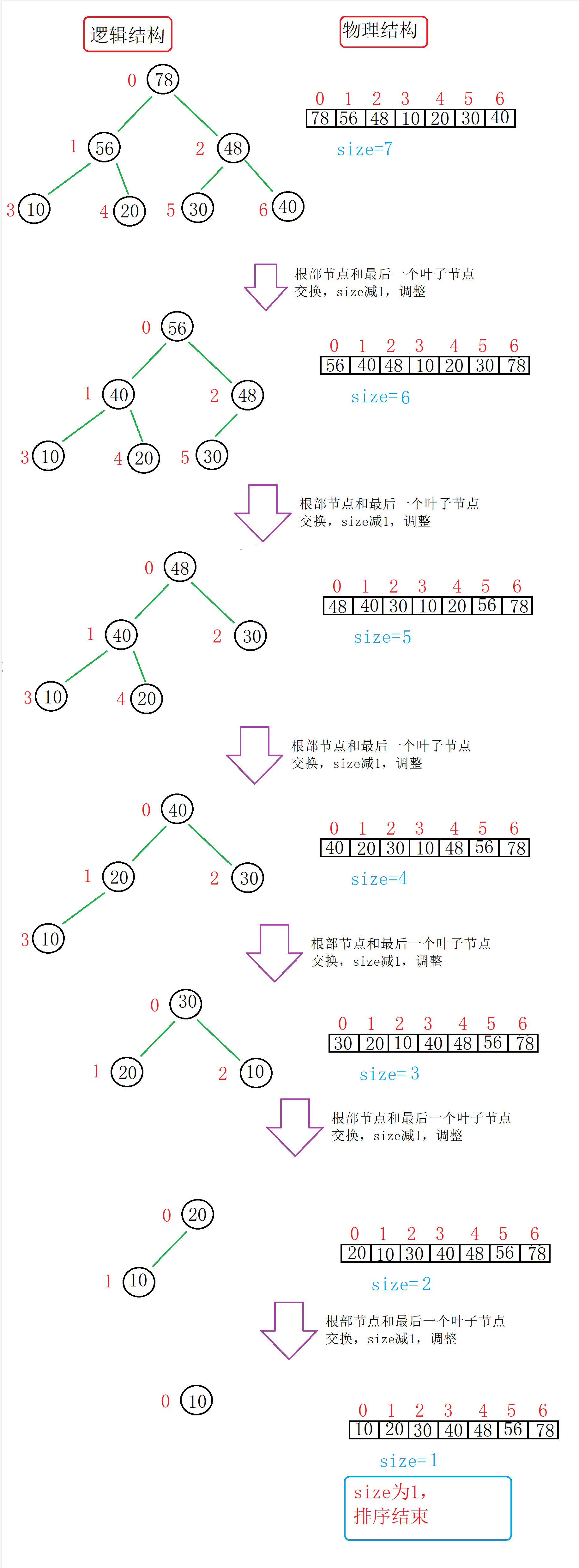
(2)堆的物理结构是数组,我们可以把根部节点(最大的数据)和最后一个叶子节点交换,将size(堆中的有效数据)减1。
(3)再进行调整来保持堆的结构,一直到size变成1。
图解(以大堆为例,怎么调整的大家可以看前一期):
代码:
void HeapSort1(int* arr, int n) { //建堆 HP hp; HeapInit(&hp); for (int i = 0; i < n; i++) { HeapPush(&hp, arr[i]); } //排序 while (hp.size > 1) { HeapSwap(&hp.a[0], &hp.a[hp.size - 1]); hp.size--; AdjustDown(hp.a, hp.size, 0); } for (int i = 0; i < n; i++) { printf("%d ", hp.a[i]); } } int main() { int arr[20] = { 78,5,8,9,7,44,55,66,99,458,41,20,0,777,458,994,2,57,7789,956 }; HeapSort1(arr, sizeof(arr) / sizeof(arr[0])); }
缺点:
(1)消耗了额外的空间来建堆。
(2)这个方式几乎要用到堆的所有功能,再使用前要写大量的接口。
【2】第二种方法(很实用)
(1)把数组原地调整成堆
这里有两种调整思路:
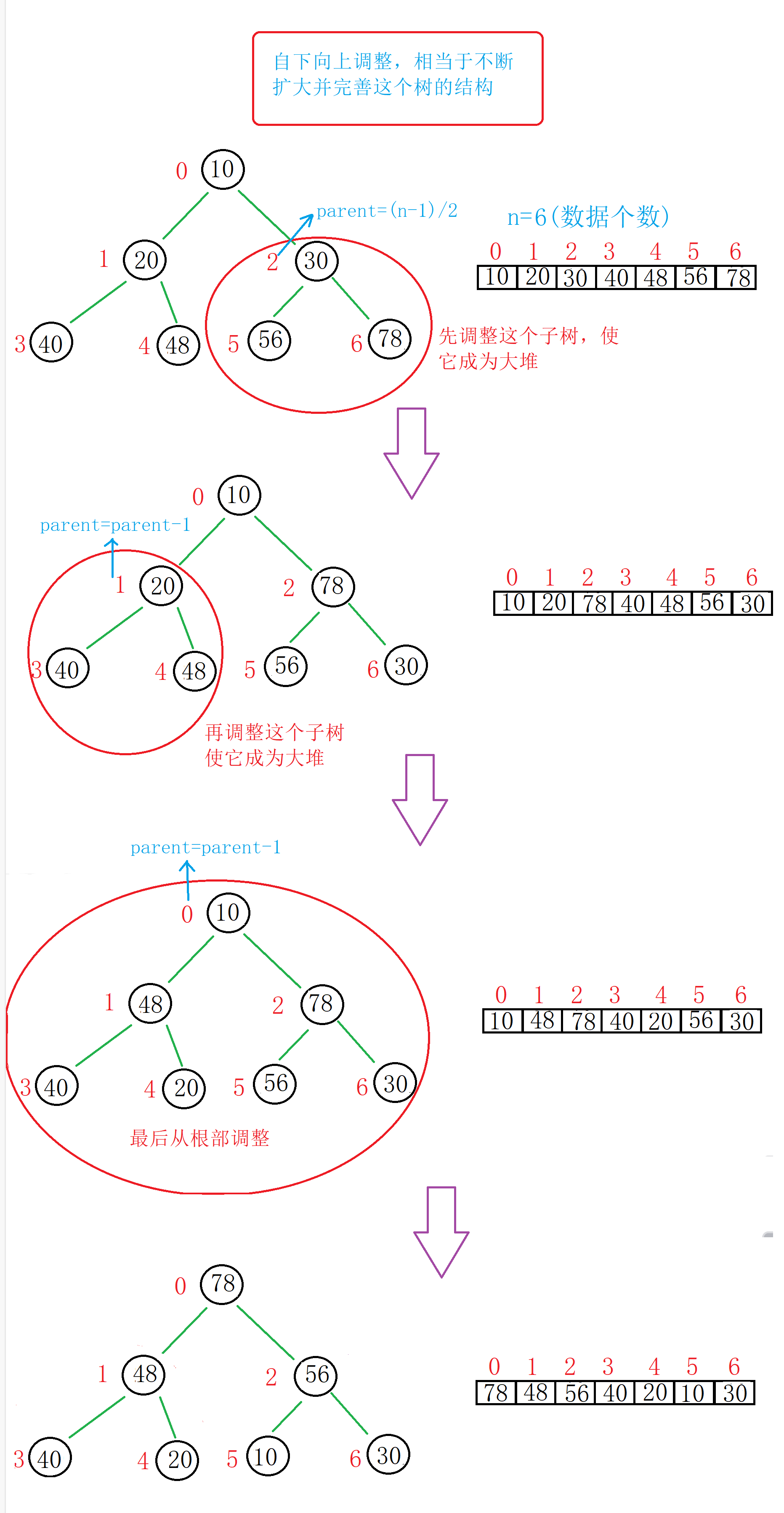
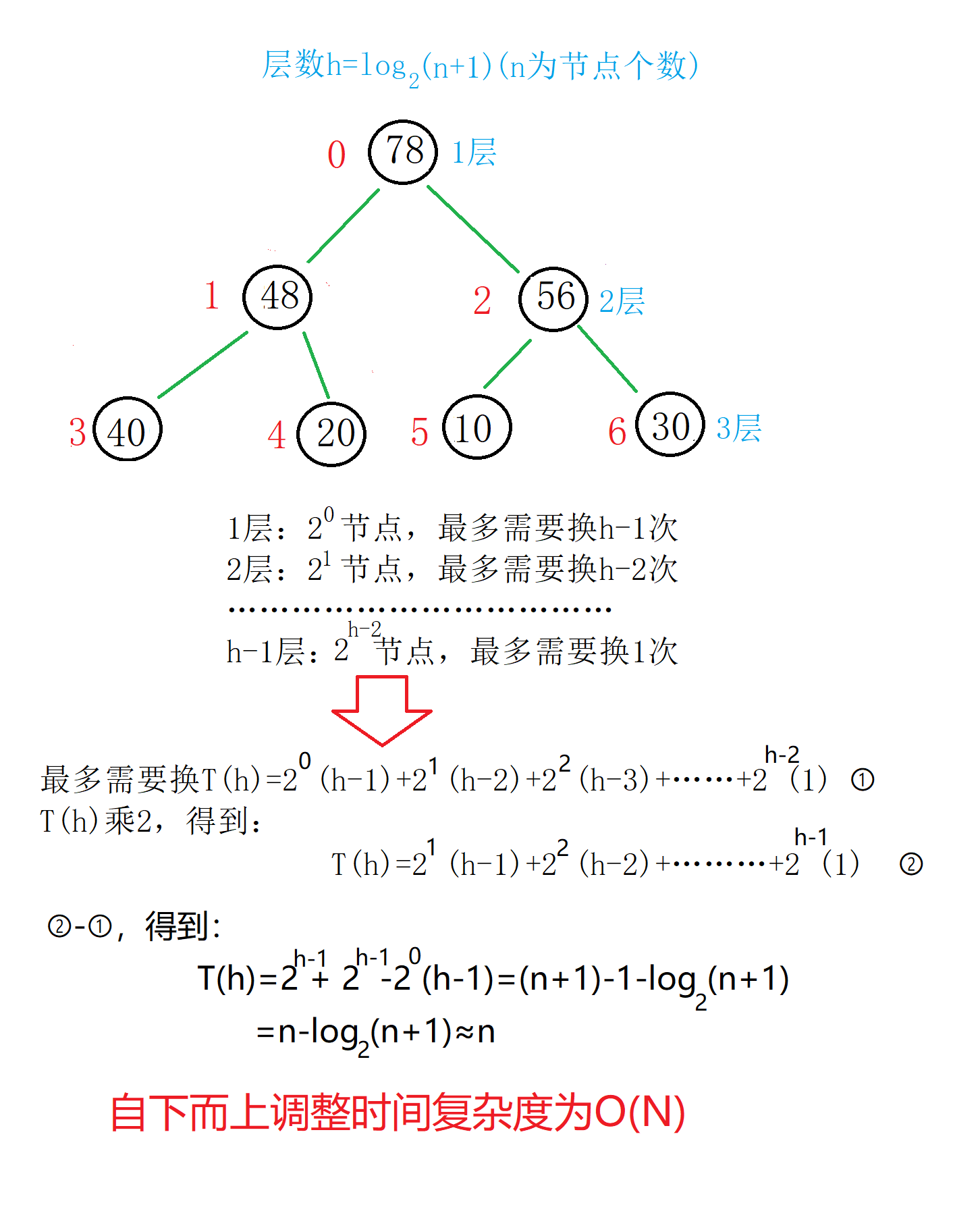
①自下而上进行调整(以大堆为例)
图解:
时间复杂度分析:
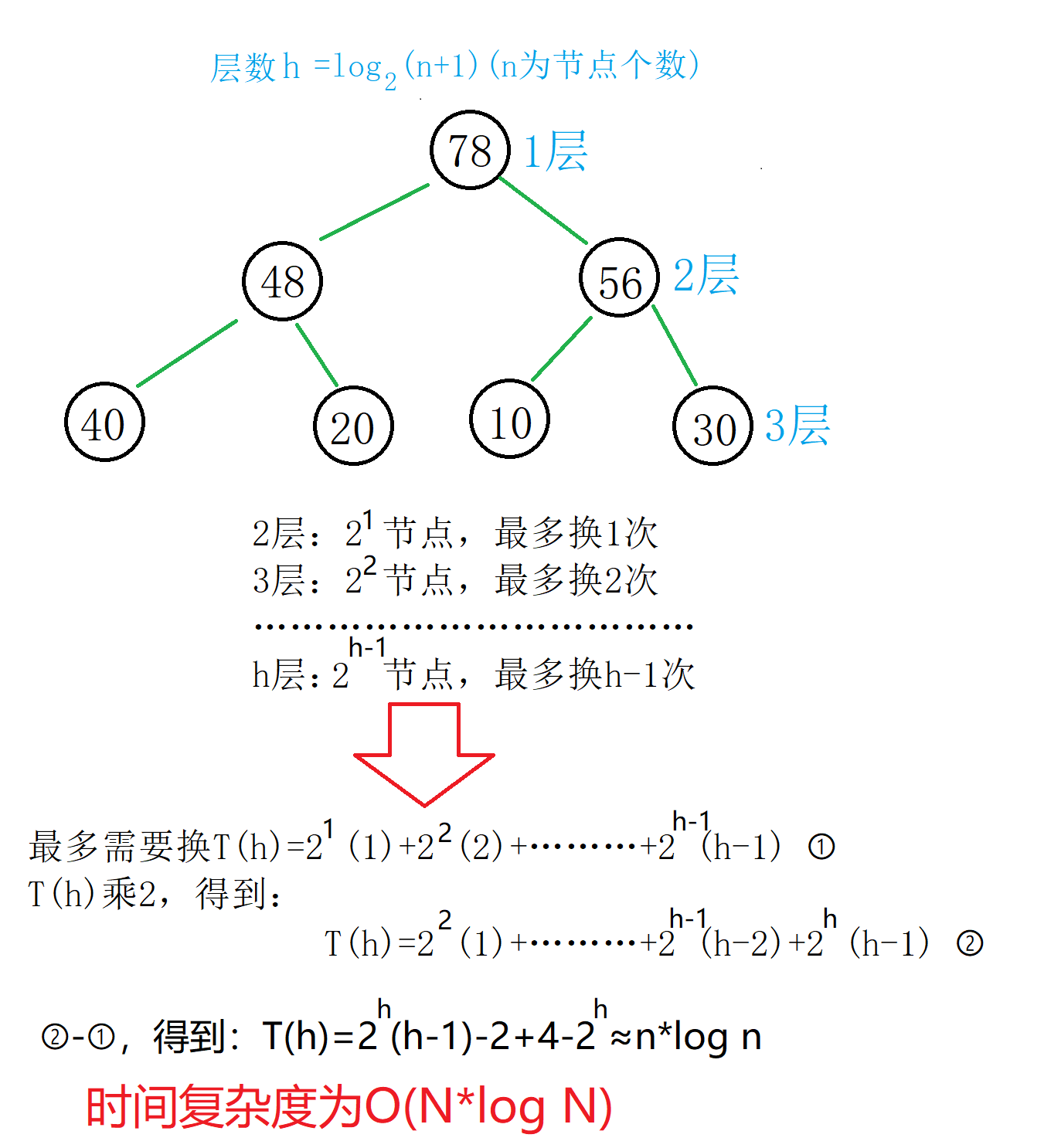
②自上而下调整(以大堆为例)
图解:
时间复杂度分析:
(2)进行排序(排序的时间复杂度和自上而下调整一致,计算思路也一致)
排序的思路和第一种方法一致:
①可以把根部节点(最大的数据)和最后一个叶子节点交换,将n(堆中的有效数据)减1。
②再进行调整来保持堆的结构,一直到n变成1。
代码:
//堆排序 void HeapSort2(int*a,int n) { //调整成堆 int parent = (n - 1) / 2; while (parent>=0) { AdjustDown(a, n, parent); parent--; } //进行堆排序 while (n>1) { HeapSwap(&a[0], &a[n - 1]); n--; AdjustDown(a, n, 0); } } int main() { int arr[] = {300,578,65,78,5,8,9,7,44,55,66,99,458,41,20,0,777,458,994,2,57,7789,956 }; HeapSort2(arr, sizeof(arr) / sizeof(arr[0])); for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++) { printf("%d ", arr[i]); } }
这个方法的优点:
(1)原地调整,不需要消耗额外的空间。
(2)只需要用到调整的接口,代码量大大减少。
堆排序的时间复杂度分析
(1)如果调整选择自上而下,整个排序时间复杂度为O(2*N*log2(N))=O(N*log2(N))。
(2)如果调整选择自下而上,整个排序时间复杂度为O(N*log2(N)+N)≈O(N*log2(N))。
综上所述,堆排序是一个时间复杂度为O(N*log2(N))的算法。
这个时间复杂度相较于冒泡是一个很大的提升。