概念

空间复杂度：是对一个算法在运行过程中临时占用存储空间大小的量度。 

空间复杂度和时间复杂度的表示方法是一样的，也使用大O渐进表示法，计算规则基本相似。空间复杂度计算的并不是程序占用的字节大小，而是变量的个数。

大O符号（Big O notation）：是用于描述函数渐进行为的数学符号。
推导大O阶方法：
1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中，只保留最高阶项。
3、如果最高阶项存在且不是1，则去除与这个项目相乘的常数。得到的结果就是大O阶

 例题解释

接下来就通过几道例题来更深入的了解一下空间复杂度吧。发车luo~

 

一（冒泡排序）

void Bubsort(int* arr, int nums)//nums是元素个数
{
	assert(arr);
	int i, j;
	for (i = 0; i < nums - 1; i++)//排序次数
	{
		int flag = 0;//判断
		for (j = 0; j < nums - 1 - i; j++)//一次排序
		{
			
			if (arr[j] > arr[j + 1])
			{
				flag = 1;
				int tmp = arr[j];
				arr[j] = arr[j + 1];
				arr[j + 1] = tmp;
			}
		}
		if (flag == 0)
			break;
	}
}

这里是冒泡排序的执行，数组中有 nums 个元素，那空间复杂度是 O(n) 吗？

临时占用存储空间大小的量度：函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了，因此空间复杂度主要通过函数在运行时候显示申请的额外空间来确定。

所以在执行函数之前，栈区已经为函数中的数组元素开辟好了固定大小的空间 ，故计算空间复杂度时，只考虑函数内部执行时所开辟的空间。因此函数中创建了常数个变量，即：O(1)

---

二（数组实现斐波那契数列）

int* Fib(size_t n)
{
	int* arr = (int*)malloc(n+1 * sizeof(int));
    assert(arr);
	arr[0] = 0;
	arr[1] = 1;
	for (int i = 2; i <= n; i++)
	{
		arr[i] = arr[i - 1] + arr[i - 2];
	}
	return arr;
}

此函数中往 arr 中动态开辟了 n+1 个整型的空间，即相当于 n+1 个变量。故：O(n)

---

三（递归实现阶乘）

int Fac(size_t n)
{
	if (n == 0)
		return 1;
	return n * Fac(n - 1);
}

在递归调用 n 次时，就会在重新创建 n 个栈帧，每个栈帧使用了常数个空间，即：O(n)

递归过程就是一个进栈和出栈的过程，当进入一个新函数时，进行入栈操作，把调用的函数和参数信息压入栈中；当函数返回时，执行出栈。 

---

四（递归实现斐波那契数列） 

int Fib(size_t n)
{
	if (n < 3)
		return 1;
	return Fib(n - 1) + Fin(n - 2);
}

 首先我们得了解一下斐波那契数列递归是如何执行的，首先 Fib（n）= Fib（n-1）+ Fib（n-2）此时的 Fib（n）是先调用 Fib（n-1）时就开始创建栈帧，重新进入函数，Fib（n-1）= Fib（n-2）+ Fib（n-3）此时 Fib（n-1）会调用 Fib（n-2）......直到调用到 Fib（2）时就函数返回，依次出栈。栈帧销毁，再递归调用右边的时会和左边重复使用同一个栈帧（即销毁的栈帧再次拿过来使用）

所以空间是可以重复利用的，不会累计计算。

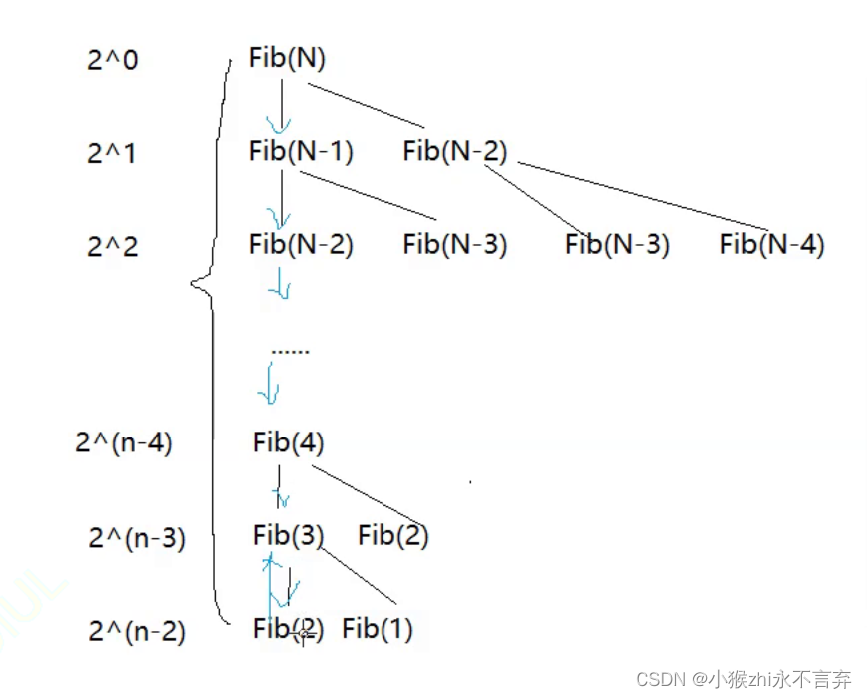
当执行 Fib（3）时会调用Fib（2），Fib（2）调用结束时函数返回一个值，并且Fib（2）开辟的栈帧销毁，此时就开始调用Fib（1）故又会创建一个栈帧，正好刚刚Fib（2）销毁了一个栈帧空间，所以这里的 1 和 2 用的是同一个栈帧空间。依次分析可以很清楚的知道空间复杂度为：O(n)

---

详细分析同一个栈帧

void test1()
{
	int a = 1;
	printf("%p\n", &a);
}
void test2()
{
	int b = 0;
	printf("%p\n", &b);
}
int main()
{
	test1();
	test2();

	return 0;
}

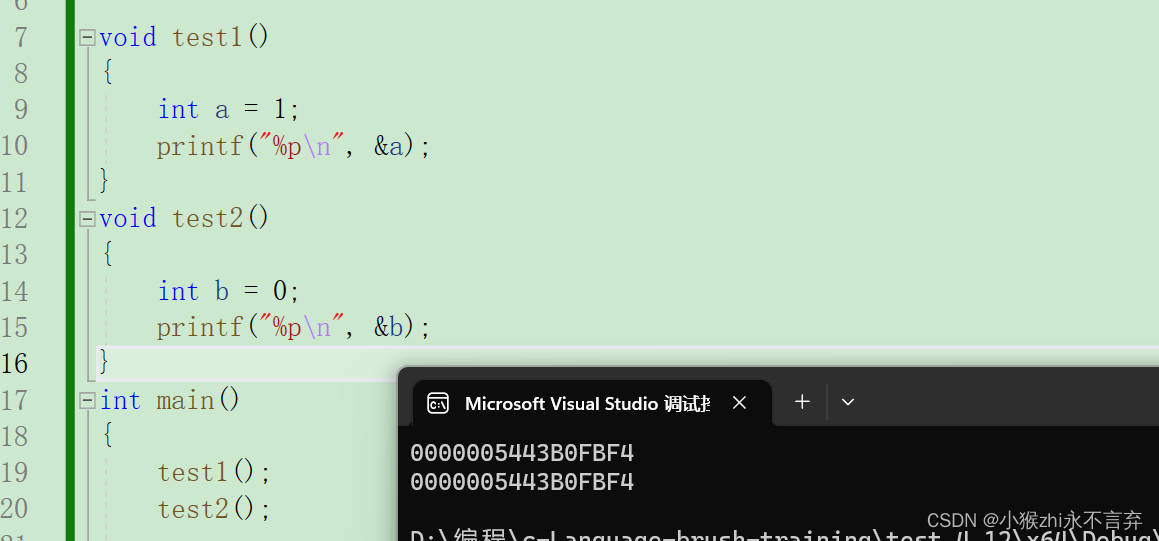
 这里调用 test1 函数时创建了变量 a 此时就在栈区开辟空间，而出了 test1 函数，为变量 a 开辟的空间也就销毁了，再次调用 test2 时，同样创建变量，栈区开辟空间 而再次开辟的空间就是 test1 销毁的空间。（销毁并不是不能用这块空间，只是该空间的数据销毁，就像和没开辟过一样，是可以继续使用的）

---