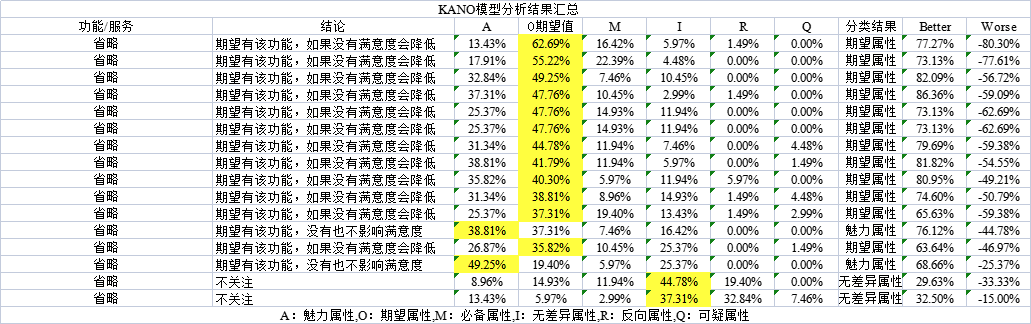
今天讲的是Leetcode第53题，最大子数组和

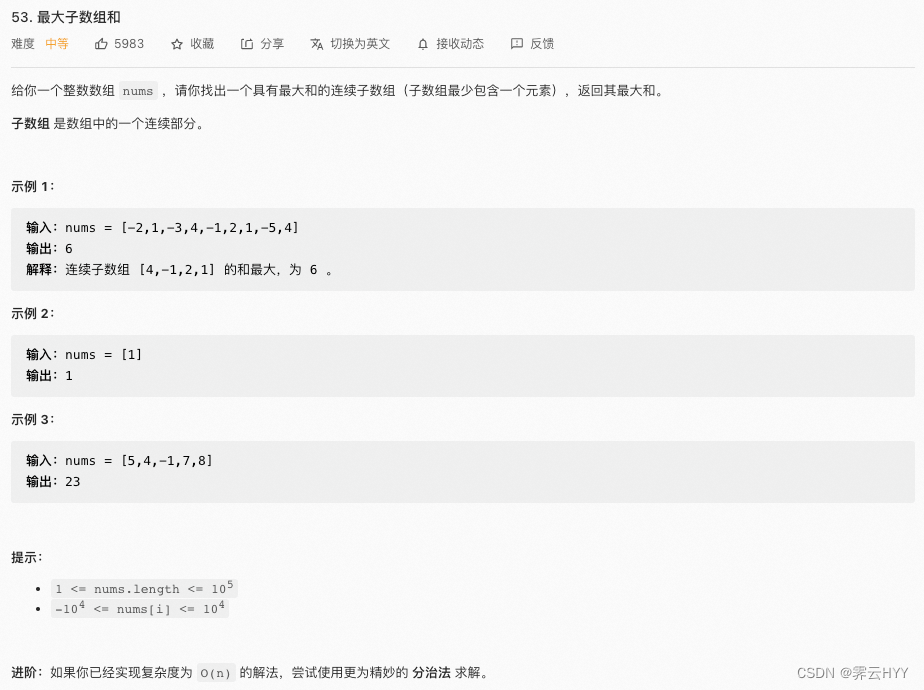
首先观察题目，题目需要我们找出具有最大和的连续子数组，直接拿题目中的示例来做一个演示，找一找什么规律下的连续子数组才能得到最大的和

先从-2开始，-2 + 1 = -1 此时我们的和是一个负数，那么无论后面的数是什么，这个数加上-1一定是更小了，所以-2这个值我们不应该加入到我们的结果子数组中
接下来是1 - 3 = -2，还是一个负数，跟上面一样，我们不需要负数，接下来的-3我们也不要了
此时从4开始找连续的子数组，4 - 1 = 3，是个正数，还能接受，就接着往后加
3 + 2 + 1 = 6，到这里为止，我们得到了迄今为止最大的子数组和
6 - 5 = 1，还是一个正数，还可以接着往后加，1 + 4 = 5，到这里为止整个数组都遍历完了
我们发现最大的子数组和是6，连续子数组为[4, -1, 2, 1]

通过我们对于示例的拆解，我们可以发现一个规律，那就是如果我们在遍历数组的时候，一旦加和为负数的话，这个和就对我们最终的解存在负面效果，所以当前遍历的数组元素就不会在我们的最大连续子数组中
同时我们在得到更大的和时，需要记录下来这个最大的值，因为后面的加和过程中，虽然整体是正数，但也不一定就是最大的，通过这两个条件我们就可以得到我们想要的最大和了

此时我们就可以得到本道题的第一个解法

public int maxSubArray(int[] nums) {
    int result = Integer.MIN_VALUE, sum = 0;
    for (int i = 0; i < nums.length; i++) {
    	// 遍历数组并进行元素的累加
        sum += nums[i];
        // 如果返回的解小于当前我们当前子数组累加的和的话，就重新对解赋值，保证这个解一直是最大的
        if (result < sum) {
            result = sum;
        }
        // 如果子数组的和是负数的话，就舍弃掉当前已经遍历过的子数组，清零后接着往后遍历
        if (sum < 0) {
            sum = 0;
        }
    }
    return result;
}

通过上面发现的规律，我们还可以使用动态规划来解决这道题，首先需要明确的是状态转移方程是怎样的，先将当前的问题进行一下拆解，如果我们要得到最大子数组和，我们需要知道哪些子问题（依旧使用示例来描述）

1. 如果我们的最大子数组包含-2，最大子数组是什么样的
2. 如果我们的最大子数组包含1，最大子数组是什么样的
3. 如果我们的最大子数组包含-3，最大子数组是什么样的
   依次类推，直到数组中的最后一个元素…
4. 如果我们的最大子数组包含4，最大子数组是什么样的

但是这样定义的话，又不能明确当前这个元素是在数组的哪个位置，不满足动态规划的「无后效性」，简单来说就是有不确定性，这个时候，就需要将子问题定义的更加严格，直接指定子问题中的元素是子数组的最后一个元素，那么我们的子问题就变成了：

1. 如果我们的最大子数组的最后一个元素是-2，最大子数组是什么样的
2. 如果我们的最大子数组的最后一个元素是1，最大子数组是什么样的
3. 如果我们的最大子数组的最后一个元素是-3，最大子数组是什么样的
   …
4. 如果我们的最大子数组的最后一个元素是4，最大子数组是什么样的

子问题定义完了，那么我们的状态转移方程应该是什么样的呢？我们从第一个子问题出发梳理一下：
如果最后一个元素是-2，那么这个最大子数组其实就是[-2]，因为也只有一个元素
如果最后一个元素是1，最大子数组和是 -2 + 1 = -1，这个情况下我们的状态转移方程是dp[i] = dp[i - 1] + nums[i]；如果我们将1这个元素换成一个负数，比如说 -1，那么这个子数组和是 -2 - 1 = -3，所以最大子数组和就是 -1，-2就被舍弃掉了
最终我们得到的状态转移方程是dp[i] = Math.max(dp[i - 1] + nums[i], nums[i ])

通过上面的分析，我们可以写出使用动态规划来解决问题的代码

public int maxSubArray(int[] nums) {
	// 将第一个元素先赋值，这样即使数组只有一个元素也不会出问题
    int result = nums[0];
    int[] dp = new int[nums.length];
    // dp[0]的解是确定的
    dp[0] = nums[0];
    for (int i = 1; i < nums.length; i++) {
    	// 状态转移方程
        dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);
        // 将子问题中最大的和存起来作为结果返回
        result = Math.max(result, dp[i]);
    }
    return result;
}

本人能力有限，可能理解表达不太到位，建议还是看Leetcode上大佬的题解来理解动态规划的思路官网题解

最后一种是题目中提到的分治法，分治法的核心思路也是将一个父问题拆成多个子问题来解决，还是拿题目的示例画一张图来理解一下

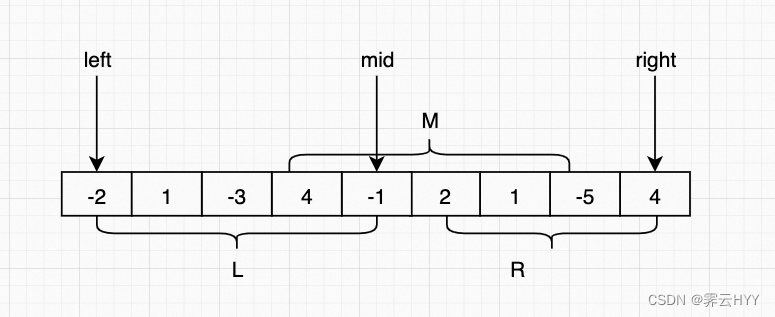
[-2,1,-3,4,-1,2,1,-5,4]作为一个完整的数组被分为3部分分别计算最大子数组和：

1. L部分计算[left, mid]
2. R部分计算[mid + 1, right]
3. M部分计算包含mid和mid + 1这两个元素的部分，左边最长延伸到left，右边最长延伸到right

同时对于L和R这两个部分，又可以递归的往下计算分别的最大子数组和，比如L部分，[-2,1,-3,4,-1]这个数组可以继续往下进行分治，直到计算出结果为止

public int maxSubArray(int[] nums) {
    return maxSubArrayDivide(nums, 0, nums.length - 1);
}

private int maxSubArrayDivide(int[] nums, int left, int right) {
    if (left == right) {
        return nums[left];
    }
    int mid = (right - left) / 2 + left;
    // 三个部分取最大的子数组和进行返回
    return Math.max(maxMid(nums, left, mid, right), 
        Math.max(maxSubArrayDivide(nums, left, mid), maxSubArrayDivide(nums, mid + 1, right)));
}

private int maxMid(int[] nums, int left, int mid, int right) {
    int sum = 0, leftSum = Integer.MIN_VALUE, rightSum = Integer.MIN_VALUE;
    // 遍历[left, mid]这个范围内最大的子数组和
    for (int i = mid; i >= left; i--) {
        sum += nums[i];
        if (leftSum < sum) {
            leftSum = sum;
        }
    }
    
    sum = 0;
    // 遍历[mid + 1, right]这个范围内最大的子数组和
    for (int i = mid + 1; i <= right; i++) {
        sum += nums[i];
        if (rightSum < sum) {
            rightSum = sum;
        }
    }
    return leftSum + rightSum;
}