1 排列permutation
排列,一般地,从n个不同元素中取出m(m≤n)个元素,按照一定的顺序排成一列,叫做从n个元素中取出m个元素的一个排列(permutation)。特别地,当m=n时,这个排列被称作全排列(all permutation)。
注:当且仅当两个排列的元素完全相同,且元素的排列顺序也相同,则两个排列相同。例如,abc与abd的元素不完全相同,它们是不同的排列;又如abc与acb,虽然元素完全相同,但元素的排列顺序不同,它们也是不同的排列
排列可分选排列与全排列两种,在从n个不同元素取出m个不同元素的排列种,当m<n时,这个排列称为选排列;当m=n时,这个排列称为全排列。
重复排列(permutationwith repetiton)是一种特殊的排列。从n个不同元素中可重复地选取m个元素。按照一定的顺序排成一列,称作从n个元素中取m个元素的可重复排列。当且仅当所取的元素相同,且元素的排列顺序也相同,则两个排列相同。
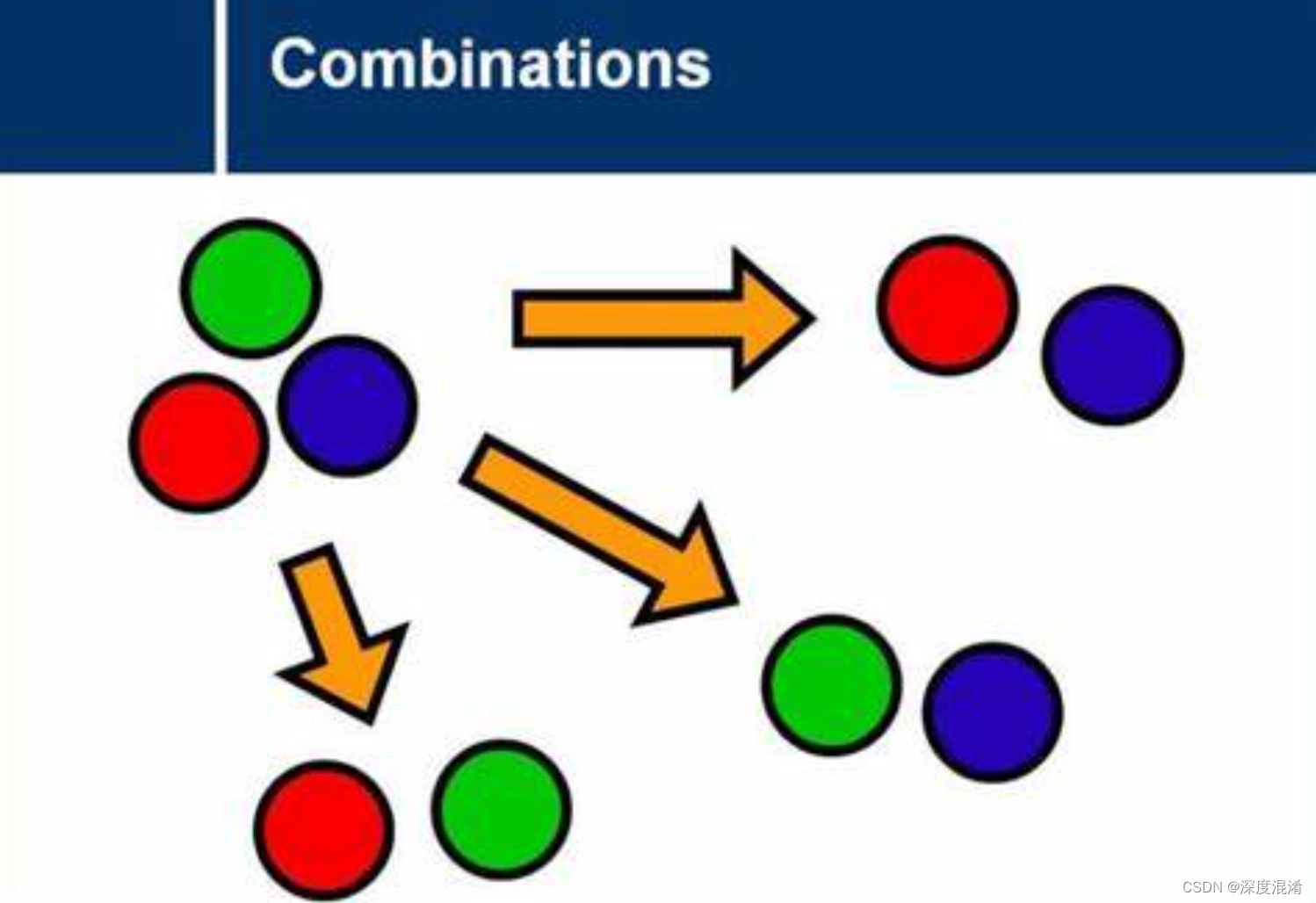
2 组合 combination
组合(combination)是一个数学名词。一般地,从n个不同的元素中,任取m(m≤n)个元素为一组,叫作从n个不同元素中取出m个元素的一个组合。我们把有关求组合的个数的问题叫作组合问题。
组合总数(total number of combinations)是一个正整数,指从n个不同元素里每次取出0个,1个,2个,…,n个不同元素的所有组合数的总和。
重复组合(combination with repetiton)是一种特殊的组合。从n个不同元素中可重复地选取m个元素。不管其顺序合成一组,称为从n个元素中取m个元素的可重复组合。当且仅当所取的元素相同,且同一元素所取的次数相同,则两个重复组合相同。
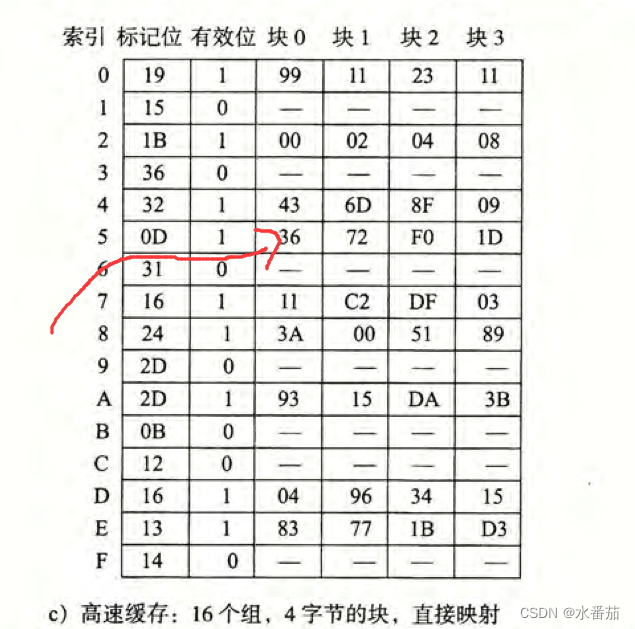
3 组合数(组合总数)的计算方法C#源代码
using System;
namespace Legalsoft.Truffer
{
public static partial class XMath
{
/// <summary>
/// 计算组合数C(M,N) M>=N
/// </summary>
/// <param name="M"></param>
/// <param name="N"></param>
/// <returns></returns>
public static int Combine(int M, int N)
{
ulong ret = 1L;
for (int i = M - N + 1; i <= M; i++)
{
ret *= (ulong)i;
}
for (int i = 2; i <= N; i++)
{
ret /= (ulong)i;
}
return (int)ret;
}
}
}4 计算组合数的数据溢出问题
上述的代码,计算 C(12,5) 是没有问题的。但是,如果计算 C(100,50)!
结果 = 0 !!!
这是因为太多的数相乘,超过了 ulong 允许的最大数,这就是数据超界的问题。
5 组合总数递归算法的C#源程序
namespace Legalsoft.Truffer
{
public static partial class XMath
{
/// <summary>
/// 计算组合数C(M,N) M>=N
/// </summary>
/// <param name="M"></param>
/// <param name="N"></param>
/// <returns></returns>
public static int Combine_Recursion(int M, int N)
{
if (M < N) return 0;
if (M <= 0 || N <= 0) return 1;
return Combine_Recursion(M - 1, N) + Combine_Recursion(M - 1, N - 1);
}
}
}递归算法可解决数值溢出问题,但会带来堆栈溢出问题,可谓“按下葫芦浮起瓢”。
6 计算组合数的追溯法(BackTrack,亦称回溯法)C#源代码
using System;
namespace Legalsoft.Truffer
{
public static partial class XMath
{
private static int num = 0;
private static ulong bestnum = 0L;
/// <summary>
/// 追溯法计算组合数
/// </summary>
/// <param name="M"></param>
/// <param name="N"></param>
/// <returns></returns>
public static ulong Combine_Backtrack(int M, int N)
{
num = 0;
bestnum = 0L;
BackTrack(1, M, N);
return bestnum;
}
/// <summary>
/// 内部递归函数
/// </summary>
/// <param name="k"></param>
/// <param name="n"></param>
/// <param name="m"></param>
private static void BackTrack(int k, int n, int m)
{
if (k > n)
{
if (num == m)
{
bestnum++;
}
}
else
{
for (int i = 0; i <= 1; i++)
{
if (i == 0)
{
BackTrack(k + 1, n, m);
}
else
{
if (num <= m)
{
num = num + 1;
BackTrack(k + 1, n, m);
num = num - 1;
}
}
}
}
}
}
}
世界上没有十全十美的人,也没有十全十美的事!
回溯算法同样存在大问题,而且是致命问题:
(1)计算效率太低,速度太慢!
(2)另外会导致堆栈溢出问题。
大数的组合 有其他计算方法,以后再介绍。
本文暂且做个了解。