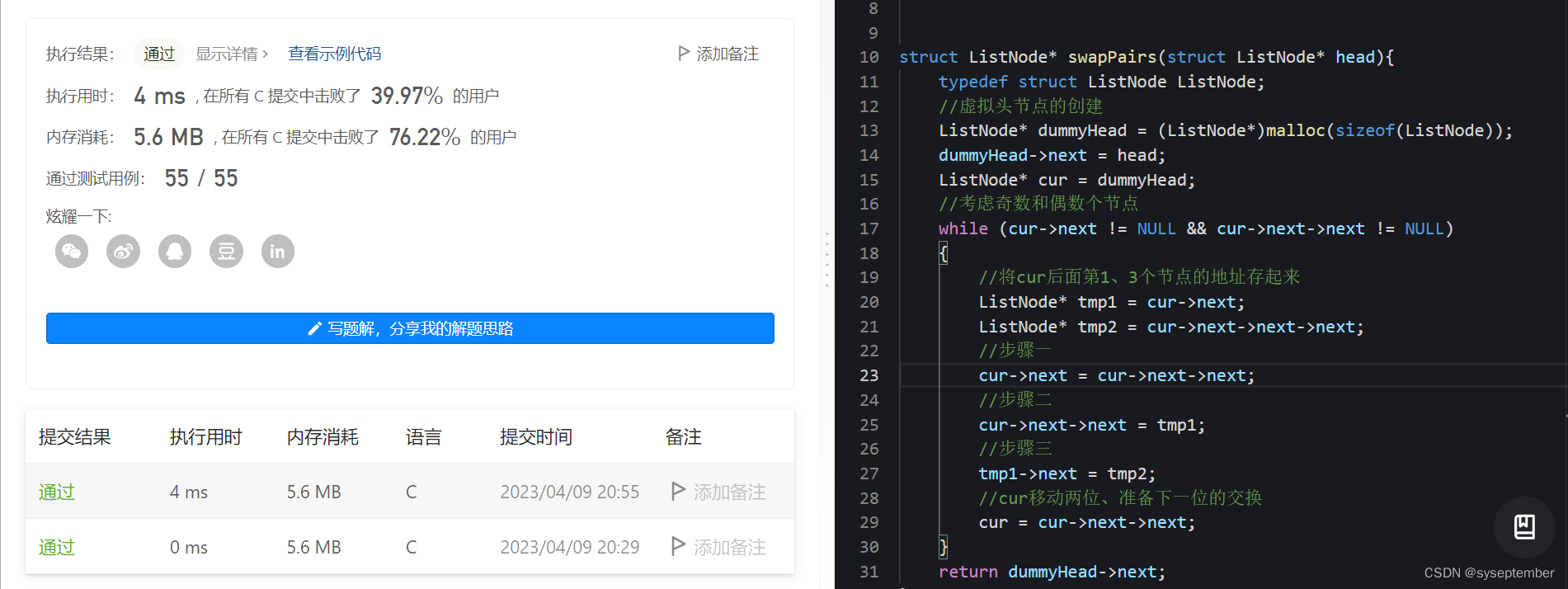
版权声明：原创不易，本文禁止抄袭、转载，侵权必究！

一、蒙特卡洛法

蒙特卡洛方法又称统计模拟法，随机抽样技术，是一种随机模拟方法，以概率和统计理论方法为基础的一种计算方法。是使用随机数来解决很多计算问题的方法。将所求解的问题同一定的概率模型相联系，用电子计算机实现统计模拟或抽样，以获得问题的近似解。为象征性地表明这一方法的概率统计特征，故借用赌城蒙特卡罗命名。

17世纪时，人们就知道用事件发生的“频率”来决定事件的“概率”。这也是蒙特卡洛法的基本思想。当样本数量足够大时，我们可以用频率去估计概率。这也是求圆周率π的常用方法。

二、求圆周率π

在只有一个随机数生成器的情况下如何估计π的大小？

当我们在（-1, 1）的范围内随机选择一个坐标（x, y）时，每个坐标点被选中的概率相等。则坐标落在直径为1的正方形中的圆的概率为：

由切比雪夫不等式可知，在生成大量随机点的前提下我们能得到尽可能接近圆周率的值。

三、Python算法实现

import numpy as np

def pi(n, batch=1000):
    t = 0
    for i in range(n // batch):     # 随机获取坐标
        p = np.random.rand(batch, 2)
        p = (p * p).sum(axis=1)     # 计算坐标平方和
        t += (p <= 1).sum()         # 平方和小于1的即为落在圆中的点
    print(4 * t / n)

pi(10 ** 4)
pi(10 ** 7)
pi(10 ** 8)

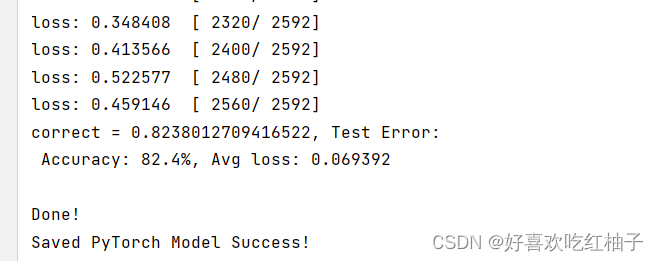
输出结果：

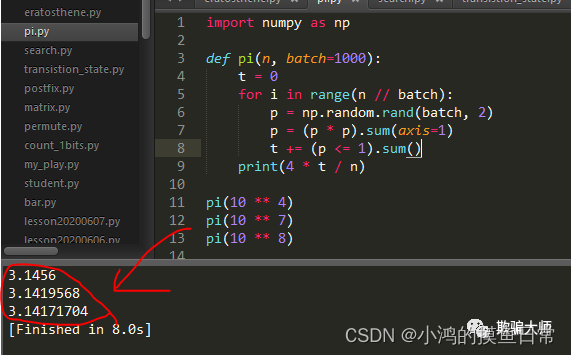
如图所示，生成大量随机点的前提下我们能得到尽可能接近圆周率的值

四、作者Info

Author：小鸿的摸鱼日常，Goal：让编程更有趣！

专注于算法、爬虫，网站，游戏开发，数据分析、自然语言处理，AI等，期待你的关注，让我们一起成长、一起Coding！

版权说明：本文禁止抄袭、转载 ，侵权必究！