📝个人主页:爱吃炫迈
💌系列专栏:数据结构与算法
🧑💻座右铭:快给我点赞赞💗
文章目录
- 1. 希尔排序
- 2. 算法思路
- 3. 算法实现
- 4. 算法性能分析
- 💞总结💞
1. 希尔排序
希尔排序(Shell Sort)是插入排序的一种,它是针对插入排序算法的改进。
希尔排序又称缩小增量排序。把所有元素按下标的一定增量分组,对每组使用插入排序算法排序;
增量随着算法的进行而逐渐缩小,当增量减至 1 时,所有元素恰被分成一组,算法便终止。
动图演示

2. 算法思路
步骤
一趟希尔排序的算法的步骤是:
- 算法先将要排序的一组数按某个增量
gap=length/2分组,每组中记录的下标相差gap。对每组中全部元素进行插入排序。- 然后缩小增量为
gap=gap/2对它进行分组,在每组中再进行插入排序。- 重复2步骤,每次缩小增量为
gap=gap/2- 当增量减到1时,整个要排序的数被分成一组,最后再进行一次插入排序,这组数排序完成。
注意:如果不熟悉插入排序的用法,请点这里:插入排序
案例演示
用快速排序算法实现5, 2, 4, 6, 1, 3的***升序排序***
第一趟:将这组数按增量gap = lenght/2 = 6/2 =3分成3组,对每组进行插入排序。

第二趟:将这组数按增量gap = gap/2 = 3/2 = 1分成1组,进行插入排序。
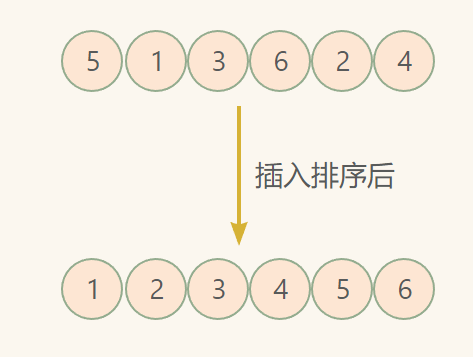
🎉🎉🎉🎉🎉🎉🎉排序完成啦~~撒花~🎉🎉🎉🎉🎉🎉🎉🎉
3. 算法实现
function shellSort(arr) {
const len = arr.length;
// 增量为每次递减二分之一的数
for (let gap = Math.floor(len / 2); gap > 0; gap = Math.floor(gap / 2)) {
// 对以增量为间隔所形成的子序列进行插入排序
// 为什么循环从 增量开始然后递增呢?
// 从增量开始,减去增量本身,得到的就是与该元素相差增量个的前一个元素
// 增量依次递增,每次减去增量本身,就依次得到了与该元素相差增量个的每一个元素
for (let i = gap; i < len; i++) {
// 得到与该元素相差增量个的前一个元素
let j = i - gap;
// 插入排序是要移动数组的,防止要插入的元素被覆盖掉
let temp = arr[i];
// 间隔增量个的前面的元素更大,就往后移动
while (j >= 0 && temp < arr[j]) {
arr[j + gap] = arr[j];
j = j - gap;
}
// 循环结束,证明循环结束位置的元素比要插入的元素小
// 所以循环结束位置的下一个位置就是要插入的位置
arr[j + gap] = temp;
}
}
}
let arr = [5, 2, 4, 6, 1, 3];
let newArr = shellSort(list)
console.log(newArr);
4. 算法性能分析
时间复杂度
📗最优
最好情况:序列是正序排列,在这种情况下,需要进行的比较操作需(n-1)次。后移赋值操作为0次。即O(n)
📕最坏
最坏情况:O(nlog2n)。
📘平均时间复杂度
渐进时间复杂度(平均时间复杂度):O(nlog2n)
结论:
1.不需要大量的辅助空间,和归并排序一样容易实现。
2. 希尔排序是基于插入排序的一种算法, 在此算法基础之上增加了一个新的特性,提高了效率。
3. 希尔排序的时间的时间复杂度为 O(n^3/2) ,希尔排序时间复杂度的下界是n*log2n。
4. 希尔排序没有快速排序算法快 O(n(logn)),但是比O(n^2)复杂度的算法快得多。因此中等大小规模表现良好,对规模非常大的数据希尔排序不是最优选择。
5. 并且希尔排序非常容易实现,算法代码短而简单。
💞总结💞
希望我的文章能对你学习希尔排序有所帮助!