Sequence
1. rnn 和 cnn

- RNN 很难并行化
- CNN很难捕捉较远的信息
2. Self-attention

- 拿每个query q去对每个 key k做attention

- 计算输出

Self-attition 矩阵计算
q i = W q a i k i = W k q i v i = W v a i Q = W q A K = W k A V = W v A (1.1) \begin{align*} q^i =& W^q a^i \\ k^i =& W^k q^i \\ v^i = & W^va^i \\ Q =& W^qA \\ K =& W^kA \\ V =& W^vA \end{align*} \tag{1.1} qi=ki=vi=Q=K=V=WqaiWkqiWvaiWqAWkAWvA(1.1)
计算输出:
A
^
=
softmax
(
K
⊤
Q
)
d
B
=
V
∗
A
^
(1.2)
\begin{align*} \hat{A} =& \frac{\text{softmax}(K^{\top}Q)}{\sqrt{d}} \\ B =& V * \hat{A} \end{align*} \tag{1.2}
A^=B=dsoftmax(K⊤Q)V∗A^(1.2)
Muti-head Self-attention

- 多头自注意力机制在 q、k、v
- qi1 之和 ki1 、vi1 操作
- 最后将多头的结果 拼接
- 对
[
b
i
,
1
b
i
,
2
]
[b^{i,1} b^{i,2}]
[bi,1bi,2]做降维即:
b i = W i [ b i , 1 b i , 2 ] ⊤ b^i = W^i [b^{i,1} b^{i,2}]^{\top} bi=Wi[bi,1bi,2]⊤ - 头的数量是超参数,一个可能的解释是,不同的头可能关注的点不一样,关注Long-Time 或者 Short-Time
Positional Encoding
解决问题:
- 在 self-attention 中没有位置信息

使用 e i e^i ei来对位置进行编码。使用: e i + a i e^i + a^i ei+ai 作为输入 - 为什么不是concat 而是相加?
- 假设有一个one-hot 的位置编码,做位置拼接。在后续的运算中,可以发现:
- W I x i W^Ix^i WIxi 是 a i a^i ai
- W P p i W^Pp^i WPpi是 e i e^i ei
- concat 和直接相加后运算等价

- W p W^p Wp 怎样计算?
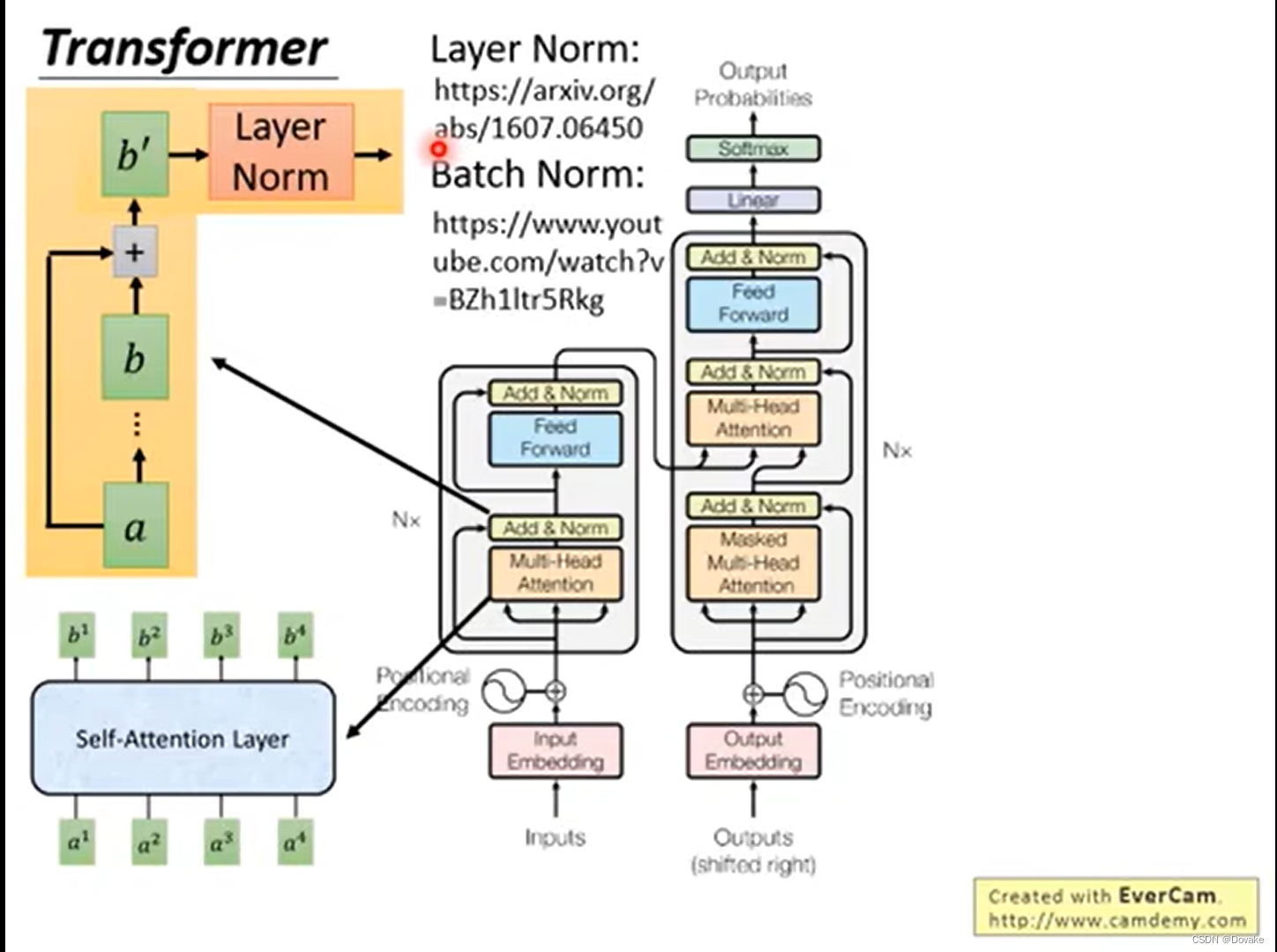
Transformer